作者简介:柏云耀 (1996-),男,硕士,主要从事新能源电动汽车研究。李顶根(1977-),男,博士,副教授,主要从事内燃机电控及清洁动力控制研究。
为了提高对于电池滥用故障的检测能力和诊断效率,针对电动汽车动力电池系统以电压、电流和电功率作为主要控制参数的特点,提出了一种基于数据分析方法的动力电池系统滥用故障检测方法。该方法采用局部异常因子(LOF)算法和感知器网络,研究由于电池滥用对电压、电流等数据的一致性和离散分布的影响。结果表明,由于故障造成的异常数据点,其LOF值远大于正常数据,在感知器分类结果中通常输出为“0”。利用LOF算法可以有效找出数据集中的异常数据点,利用LOF算法处理后的数据对感知器进行训练,可以对数据集进行快速分类,进而判断电池是否发生了滥用故障。该方法可为动力电池系统故障检测提供参考。
An abuse fault detection of power battery system based on data analysis method, aiming at the characteristics that electric vehicle battery system put voltage, current and electric power as its main control parameters, was proposed to improve fault detection capability and diagnostic efficiency for battery abuse failures. By using local anomaly factor (LOF) algorithm and perceptron network, the effects of battery abuse fault on data consistency and discrete distribution of voltage and current were studied. The results showed that the LOF value of the abnormal data points caused by the fault was much larger than the normal data, and the output was usually “0” in the perceptron classification result. Obviously, local anomaly factor algorithm can effectively find the abnormal data points in the data set. Using the data processed by the LOF algorithm to train the sensor, the data set can be quickly classified to determine whether the battery has been abused. Therefore, the method can provide a reference for fault detection of the power battery system.
作为新兴的车用动力来源, 锂离子动力电池在技术上依然存在一些问题和瓶颈, 由于滥用导致的电池系统事故时有发生。电池滥用是动力电池系统常见的故障类型, 主要有过充电、在高温环境下使用导致内部过热和电池壳体损坏导致内部短路等几种故障形式。因此, 加快电动汽车电池系统故障诊断和安全管理的研究就变得尤为重要[1, 2, 3]。
当前, 对于电池滥用故障的研究多采用实验室模拟的手段。常见方法主要包括采用针刺的方法模拟机械碰撞导致电池壳体损坏引发电池热失控[4], 采用过充电或过放电的方式模拟电池滥用故障[5, 6], 采用烤箱或直接加热的方式模拟电池在高温环境下的滥用故障[7, 8]。但这些方法均是在确定了滥用故障类型的情况下进行试验, 对于实际使用中发生未知类型的滥用故障, 这些方法缺乏有效的故障判别和检测手段。同时, 实验中对于电池故障的判断和分析主要依靠直观的实验现象和简单的数据分析, 对于动力电池实际使用中发生滥用故障所产生的大量数据缺乏有效的处理手段。而在使用中产生大量电流、电压等数据正是动力电池系统的一大特征。
因此, 为了克服一般实验手段对电池滥用故障类型缺乏有效判别方法和对故障产生的大量数据缺乏有效处理手段的弊端, 本文提出了基于局部异常因子(local outlier factor, LOF)算法和感知器网络的电池滥用故障诊断处理方法。利用LOF算法找出数据集中的异常数据点, 利用经过算法处理后的数据对感知器进行训练, 在感知器中对数据集进行快速分类, 进而判断电池是否发生了滥用故障。
LOF算法是一种聚类分析方法。
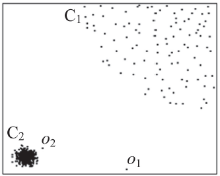
图1所示为一个聚散分布非常明显的数据集。在这个数据集中, C1区域内各点的距离比较平均, 点密度及离散分布情况基本一致, 可以视作同一簇数据。同理, C2区域内的点也可以认为是同一簇数据。而对于图中的o1、o2点, 它们相对于C1、C2区域内的点, 与其他点的间距较大, 相对孤立, 可以视为异常数据点。LOF算法, 正是一种能够实现在C1和C2这种密度差异巨大的数据集合中, 找出异常点的通用性算法。
下面简单介绍LOF算法的有关概念:
(1)在数据集中任取p、o两点, p点和o点之间的距离为$d_{p, o}$。
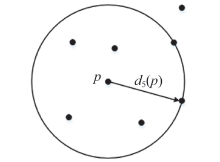
(2)第k距离(k-distance)$d_{k}(p)$。定义$d_{p, o}$=$d_{k}(p)$, 同时满足:①在集合中至少有不包括点p在内的k个点$o^{'}\in C \lbrace x≠ p \rbrace$, 满足$d_{(p, o^{'})}$≤ $d_{(p, o)}$; ②在集合中至多有不包含点p在内的k - 1个点$o^{'}\in C \lbrace x≠ p \rbrace$, 满足$d_{(p, o^{'})}$≥ $d_{(p, o)}$。简单来讲, 点p的第k距离, 就是距离p点第k远的点到点p的距离, 如图2。图中显示的是p点的第5距离, 即距离p点最近的5个点中, 与p点距离最远的点到p点的距离。
(3)p点第k距离邻域(k-distance neighborhood of p)$N_{k}(p)$, 是在点p的第k距离以内的所有点, 其中也包括第k距离的点。简单来讲, 就是以p点为圆心, op距离为半径画圆, 圆内及圆上所有除过p点的点都是点p的第k距离邻域内的点。
(4)可达距离(reach-distance)。点o到点p的第k可达距离定义为:
$ Reach-distance_{k(p, o)}=max \lbrack k-distance(o), d_{(p, o)}\rbrack $
可以看出, 点o到点p的第k可达距离, 是点o的第k距离和o、p间真实距离这两者中的最大值。距离点o最近的k个点, o到它们的可达距离是相同的, 都是$d_{k}(o)$。
(5)局部可达密度(local reachability density, LRD)。点p的局部可达密度表示为:
$LRD_{k}(p)=\frac{1}{\frac{\sum_{o\in N_{k}(p)}reach-dist_{k(p, o)}}{|N_{k}(p)|}}$ (1)
在数学上, 点p的局部可达密度表示为点p的第k邻域内点到p的平均可达距离的倒数。值得注意的是, 公式中采用的平均可达距离, 是邻域点到p的平均可达距离, 而不是点p到其领域点的平均可达距离, 两者不能混为一谈。而对于重复点, 则要在计算时将其剔除。局部可达密度的含义可以理解为:这是一个表示数据点密度的值, 值越大, 数据越集中, 则越可能属于同一簇数据, 相反, 值越小, 数据越分散, 则越可能是异常点。如果p点和周围邻域点之间相互距离较小, 很可能属于同一簇数据, 那么其可达距离就很可能是较小的, 其可达距离之和也必然较小, 密度值较高; 相反, 若p和周围领域点相互距离较远, 那么可达距离则很可能是两点间的真实距离, 可达距离之和较大, 密度较小, 是离群点。
(6)局部异常因子(LOF)。点p的局部异常因子表示为:
$LOF_{k}(p)=\frac {\sum_{o\in N_{k}(p)} \frac{LRD_{k}(o)}{LRD_{k}(p)}} {|N_{k}(p)|}$ (2)
上式的数学意义表示点p的邻域点的局部可达密度与点p的局部可达密度之比的平均数。如果这个比值接近1, 说明p点附近邻域点的密度相差不大, p点很有可能和其领域点是同一簇数据; 如果这个比值小于1, 说明p点附近数据点的密度更大, 数据更密集, p为密集点; 反之, 如果这个比值大于1, 说明p点可达密度较其领域点较小, p点附近数据较少, 或p点距离数据点较远, 更可能是异常点。
总的来说, LOF算法是一个通过比较每个点p和其邻域点的密度的大小来判断该点是否为异常点的算法。如果点p的密度越小, 则点p附近的数据点越少, 点p越可能是异常点。而密度主要是通过距离来计算的, 点与点之间距离越近, 密度则必然越大, 距离越远, 密度必然越小。同时, LOF算法主要计算数据点的第k邻域距离, 即只考虑第k距离的局部, 而不需要全局计算, 因此, 对于多个局部分布的密集数据簇的处理具有很强的可靠性[9, 10, 11, 12]。
本文数据主要来源于某整车企业车辆实际运行数据, 记录了电池发生滥用故障时的电压、电流、电功率等数据的变化。使用局部异常因子算法对由于滥用导致内部过热的电池故障数据进行分析处理, 对照故障现象, 确定故障引起的异常数据点, 将此数据作为训练数据代入单层感知器(一种用于数据简单线性划分问题的单层神经网络)中进行训练, 将未知是否发生故障的另一组电池数据作为待分类数据。利用训练好的感知器对该数据进行分类, 判断是否发生故障。
选取电池内部过热数据进行算法的验证分析。根据故障现象的说明, 电池在13分5秒左右开始冒烟, 在16分11秒时停止数据采集。电池故障前重量为41.125 g, 电池发生故障后重量为34.825 g, 这些现象说明在电池内部过热的情况下, 电池本身发生了明显变化, 需要关注的正是从冒烟到结束这一阶段的数据。
利用LOF算法对发生滥用故障的电池数据进行处理, 依靠Matlab软件, 首先计算出在二维坐标轴上任意两点之间的距离, 然后选取合适的第k距离, 由于算例中数据样本数量不多, 极差不大, 取k = 5, 计算出任意点的第5距离(5-distance)和第5可达距离(reach-distance5), 将reach-distance5的结果带入式(1), 得到任意点在其第5领域内的局部可达密度(LRD5), 再将各点的LRD5代入式(2), 得到k取5的情况下的各点局部异常因子(LOF5), 结果如表1所示。
| 表1 发生滥用故障电池各数据点LOF值 Table 1 LOF value of battery abuse failures |
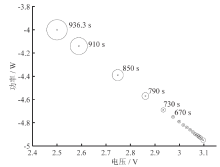
为便于直观观察, 利用Matlab软件绘图。如图3所示。
由于各数据点对应的LOF值较小, 在图3中以各点所在位置为圆心, 各点LOF值扩大十倍后的值为直径作圆, 以便于观察各点LOF值的大小。
利用表1的数据训练感知器。首先根据表1中电压和功率各自的最大值和最小值作为初始数据创建感知器, 然后将从70 s到670 s区域内的正常数据的对应期望输出设置为1, 从730 s到936 s区域内的异常数据对应期望输出设置为0。以表1中各点的电压和电功率作为训练数据, 其对应的期望输出值作为目标向量代入感知器对感知器进行训练, 获得合适的权值和偏移量, 使感知器具有数据分类能力, 最后将需要判断是否发生故障的电池数据代入感知器中进行分类。分类结果如表2所示。
| 表2 未知故障电池数据感知器分类结果 Table 2 Data perceptron classification results of the heating experiment of unknown failure battery |
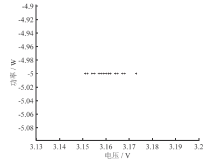
利用Matlab软件对感知器分类结果绘图, 如图4。在图4中, 感知器输出结果为0的是故障导致的异常数据点, 用“ o” 表示; 输出结果为1的是工作正常的数据点, 用“ +” 表示。图中的分界线, 是以训练后的感知器的权值为斜率, 偏移量为截距的一次曲线。
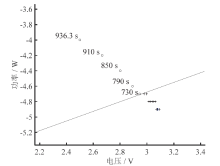 | 图4 未知故障电池加热实验数据感知器分类结果Fig. 4 Data perceptron classification results of the heating experiment of unknown failure battery |
另外, 为了验证方法的可靠性, 采集一组正常电池充电数据作为对照组。代入感知器进行分类, 结果如表3。
| 表3 对照组数据感知器分类结果 Table 3 Data perceptron classification results of control group |
利用Matlab分类结果如图5所示。
根据表1和图3所示, 大部分数据的LOF值都约为1, 而从670 s到936 s故障发生后采集到的数据点的LOF值都较大, 均大于1, 在图3中, 这部分数据也脱离故障发生前正常数据所在的集中区域, 是离散分布的异常数据点。同时, 伴随故障发生时间增长, 故障发展程度深入, 对应数据点的LOF值也逐渐增大, 偏离正常数据集中区域的距离增大。处理结果符合实验现象, 证明利用LOF算法筛选故障数据点的方法是可行的。
根据表2、表3、图4和图5所示, 发生滥用故障的电池数据经过感知器处理后, 正常工作时采集的数据输出结果为1, 发生故障后采集的数据输出结果为0, 位于分界线的上方。对照组数据分类结果表明, 正常充电数据经过感知器分类后的结果均为代表工作正常的“ 1” 。证明训练后的感知器分类结果是有效的。
分类结果与实验现象相吻合, 证明经过训练的单层感知器网络对于电池是否发生滥用故障具有判断功能。将待诊断的电池数据代入感知器进行处理, 若输出结果均为1, 表明电池未发生故障, 工作正常。若输出结果中有“ 0” 输出, 表明电池发生了故障。同时, 根据感知器的分类结果, 能够确定具体的异常数据点及其范围, 确定电池故障开始的时间和发展的时间, 在本次实验中, 感知器得出的故障开始时间为730 s, 实际试验中为785 s, 判断误差为55 s, 具有参考价值。因此, 结合LOF算法的处理结果和实验现象, 能够估计电池故障发展的深度, 推断电池状态。
以动力电池系统滥用故障为主要研究对象, 基于LOF算法和单层感知器网络等数据分析手段, 提出了一种电池滥用故障的诊断方法。经过实验数据验证, 得出以下结论:
采用LOF算法和感知器相结合的数据处理方法, 可以快速确定数据集中的异常数据点。能够有效帮助研究人员快速处理大量数据, 并针对异常数据进行研究。
感知器分类根据相同类型故障引起的异常数据间的关联性, 能够有效判断电池是否发生故障, 故障的类型以及故障发生的时间及进行深度。可以为进一步的故障研究提供参考依据。
由于单层感知器只有单一的权值和偏移量, 因此对具有复杂关联性的数据处理能力不足。作者下一步将引入多层感知器和深度学习, 进一步提高该方法的数据处理能力。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|