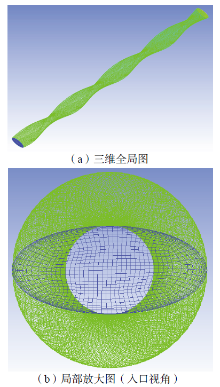
本文着重分析三维变形管扭曲管段的长短轴比（A/B）、螺距（S）对管内积灰性能的影响, 因此, 对管长相同、长短轴比不同的三维变形管分别建立几何模型。管长（l）为1 m, 长短轴比为2.2及螺距为0.5 m的几何模型如图2所示。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 三维变形管几何模型Fig. 2 Geometric model of three-dimensional deformation tube

计算域内的含尘气流为空气和灰尘的气固两相流, 为提高数值模拟计算效率, 计算域内的网格为结构化网格, 数值模拟计算所用几何模型的具体参数见表1。

表1

Table 1

表1(Table 1)

表1 不同三维变形管的几何参数 Table 1 Geometric parameters of different three-dimensional deformation tubes 模型序号 A / mm B / mm S / mm l / mm 1 64 29 500 1 000 2 64 29 300 1 000 3 64 29 200 1 000 4 50 46 500 1 000 5 58 37 500 1 000

表1 不同三维变形管的几何参数 Table 1 Geometric parameters of different three-dimensional deformation tubes

计算域如图2所示, 烟气由入口流入, 出口流出。为保证数值模拟的可靠性, 计算域网格划分时对管壁处网格适当加密（近壁面处第一层网格高度Δ h须保证无量纲量y⁺≈ 1^[16]）。

${{y}^{+}}=\frac{{{u}^{* }}\Delta h}{\upsilon }$ (1)

式中:Δ h为近壁面处第一层网格高度, m; u^* 为近壁面空气流速, m/s; $\upsilon $为空气运动黏度, m²/s。

随着网格的加密, 数值解会逐渐收敛至接近精确解, 然而随着网格数量的增多, 计算时长将会大幅增大, 且当网格数增大到一定程度时, 计算结果将不会明显变化。因此, 考虑到计算精度与计算效率的平衡, 有必要进行网格无关性验证以寻找恰当的网格划分方案。对于管长为1 m、长短轴比为2.2、螺距为0.5 m的三维变形管（模型1）划分3种体系的网格, 并在相同的入口速度边界条件（12 m/s）、相同颗粒粒径（30 μ m）和相同数值计算方法进行数值模拟, 得到的计算结果如表2所示。可以发现, 随着网格数量的增加, 沉积率逐渐增大, 当网格数增加至181 678时, 沉积率不再随网格数量的增加而增大, 因此可以确定该数值模型下对应的适宜网格数量为181 678（如图3所示）, 以此方法进行网格无关性验证, 最终确定计算域对应不同烟气流速的网格数量为200 000 ~ 500 000个。

表2

Table 2

表2(Table 2)

表2 网格无关性验证 Table 2 Validation of grid independence 网格类型 网格数量 沉积率R / % 近壁面未加密 168 976 34.3 近壁面适当加密 181 678 35.7 整体加密 219 517 35.8

表2 网格无关性验证 Table 2 Validation of grid independence

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 计算域结构化网络Fig. 3 Structural grids of computational domain

气相边界条件:入口的边界条件为速度入口, 考虑三维变形管管内积灰为干灰沉积, 故设入口烟温为440℃, 烟气流速为8 ~ 21 m/s, 出口边界条件设为压力出口, 三维变形管壁面设为无滑移壁面边界条件, 壁温设为200℃, 忽略壁厚, 近壁面采用增强壁面函数处理。

固相边界条件:固相灰尘颗粒以面源方式由入口进入计算区域, 认为其速度与烟气入口流速一致, 入口灰尘颗粒质量浓度为30 ~ 70 g/m³, 灰尘颗粒密度为2 400 kg/m³, 平均灰尘颗粒直径分别为30 μ m、50 μ m、70 μ m, 服从罗辛-拉姆勒（Rosin-Rammler）分布, 壁面设为捕捉（trap）类型。

气固两相流在管壁上的灰粒沉积过程较为复杂, 相关的沉积理论和模型较多, 但普适性有限, 由于灰尘颗粒所占的体积分数小, 灰粒之间的相互作用及灰粒对烟气流动所造成的影响均可忽略。因此, 气相视为不可压缩流体, 气相（连续相）流动模型用可实现的k-ε 两方程（Realizable k-ε ）模型; 对于固相颗粒选用离散相模型, 并采用随机轨道模型反映灰尘颗粒的运动轨迹^{[20, 21]}。

1.2.1 气相控制方程

气相（连续相）流动控制方程为质量守恒方程、动量守恒方程、能量守恒方程、湍动能方程以及湍流耗散率方程, 计算分别如下。

质量守恒方程

$\frac{\partial \rho }{\partial \tau }+\frac{\partial \left( \rho {{u}_{j}} \right)}{\partial {{x}_{j}}}=0$ (2)

动量守恒方程

$\rho \frac{\partial {{u}_{i}}}{\partial \tau }+\rho {{u}_{j}}\frac{\partial {{u}_{i}}}{\partial {{x}_{i}}}=-\frac{\partial p}{\partial {{x}_{i}}}+\mu \frac{\partial }{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)$ (3)

能量守恒方程

$\rho \frac{\partial T}{\partial \tau }+\rho \frac{\partial \left( {{u}_{i}}T \right)}{\partial {{x}_{i}}}=-p\frac{\partial {{u}_{i}}}{\partial {{x}_{i}}}+\lambda \frac{\partial }{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)$(4)

湍动能方程

$\begin{align} & \rho \frac{\partial k}{\partial \tau }+\rho \frac{\partial \left( {{u}_{j}}k \right)}{\partial {{x}_{j}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +\frac{{{\mu }_{i}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+ \\ & {{\eta }_{\text{t}}}\frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-\rho \varepsilon \end{align}$ (5)

湍流耗散率方程

$\begin{align} & \rho \frac{\partial \varepsilon }{\partial \tau }+\rho \frac{\partial \left( {{u}_{j}}\varepsilon \right)}{\partial {{x}_{j}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +\frac{{{\mu }_{\text{t}}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+ \\ & {{c}_{1}}\rho {{S}^{* }}\varepsilon -{{c}_{2}}\rho \frac{{{\varepsilon }^{2}}}{k+\sqrt{\upsilon \varepsilon }} \end{align}$ (6)

式中:ρ 为空气密度, kg/m³; u为空气流速, m/s; T为空气温度, K; μ 为动力黏度, N∙ s/m²; λ 为空气导热系数, W/(m∙ K); k为湍动能, m²/s²; ε 为湍动耗散率; 下标t指与湍动特性有关; σ _k和σ _ε 为湍动能和湍动耗散率对应的普朗特数, 分别为1.0和1.2; ${{c}_{1}}=\text{max}\left[ 0.43{\eta }/{\eta +5}\; \right]$; ${{c}_{2}}=1.9$; ${{\eta }_{\text{t}}}={{{S}^{* }}k}/{\varepsilon }\; $; ${{S}_{i, j}}={\left( {\partial {{u}_{i}}}/{\partial {{x}_{i}}}\; +{\partial {{u}_{j}}}/{\partial {{x}_{j}}}\; \right)}/{2}\; $; ${{S}^{* }}=\sqrt{2{{S}_{i, j}}{{S}_{i, j}}}$; ${{\mu }_{\text{t}}}={{c}_{\mu }}\rho {{k}^{2}}/\varepsilon$, 为湍动黏度, N∙ s/m²; ${{c}_{\mu }}$为常系数, 为0.085。

1.2.2 固相颗粒运动方程

固相灰尘颗粒密度远大于气相密度, 认为颗粒主要受重力、曳力和惯性力的作用, 单个灰尘颗粒的运动方程可以写为:

$\frac{\text{d}{{u}_{\text{p}}}}{\text{d}\tau }=\frac{u-{{u}_{\text{p}}}}{{{\tau }_{\text{r}}}}+\frac{g\left( {{\rho }_{\text{p}}}-\rho \right)}{{{\rho }_{\text{p}}}}+F$ (7)

式中:F为单个灰尘颗粒额外受到的附加力, N; $\left( u-{{u}_{\text{p}}} \right)/{{\tau }_{\text{r}}}$为单个灰尘颗粒受到的曳力, N; u为气相流体流速, m/s; u_p为固相颗粒流速, m/s; ρ 为气相流体密度, kg/m³; ρ _p为固相颗粒密度, kg/m³; τ _r为灰尘颗粒的弛豫时间, 其计算如下:

${{\tau }_{\text{r}}}=\frac{4{{\rho }_{\text{p}}}d_{\text{p}}^{2}}{3{{C}_{d}}Re{{\mu }_{\text{p}}}}$ (8)

式中:d_p为固相颗粒直径, m; μ _p为灰尘颗粒的黏度, N⋅ s/m²; C_d为阻力系数; Re为相对雷诺数, 其计算如下

$Re=\frac{\rho {{d}_{\text{p}}}\left| u_{\text{p}}^{{}}-u \right|}{\mu }$ (9)

1.2.3 灰尘颗粒沉积计算模型

三维变形管管内的积灰是细灰沉积形成沉积层和粗灰破坏沉积层的动态过程, 细灰在积灰初始阶段在管壁上的沉积量不断增加, 粗灰对细灰沉积层的破坏强度较弱, 积灰量不断增加。当积灰达到一定程度时, 粗灰破坏细灰沉积层的效果逐渐增强, 沉积在壁面上的细灰量减少, 最后直至细灰沉积量与由于粗灰破坏减少的沉积量达到动态平衡, 积灰量则不再发生变化。

灰尘颗粒沉积率计算式如下

$R={{{N}_{\text{accretion}}}}/{{{N}_{\text{inlet}}}}\; $ (10)

式中:N_accretion为沉积的灰尘颗粒数量; N_inlet为入射的灰尘颗粒总量。

对于三维变形管, 经过大量数值计算, 发现当柯朗数为10时, 其管内的烟气流动与传热较易收敛, 数值计算过程中所采用的时间步长Δ τ 遵从下式

$\Delta \tau ={C\times L}/{5V}\; $ (11)

式中:C为柯朗数; L为网格特征尺寸, 为近壁面第一层网格高度; V为特征流速, 为三维变形管内气流流速; 故时间步长为5.6 × 10^-5 ~ 1.48 × 10^-4s。

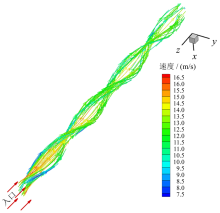
相关研究表明, 由于三维变形管的螺旋扭曲形变, 使流体在三维变形管内流动时产生以旋转为主要特征的复杂流动, 并且在管内垂直于主流方向上产生二次流, 从而促进传热^[17]。灰尘颗粒是由气流携带而随气流一起流动, 直径为30 μ m的灰尘颗粒在三维变形管（A/B = 2.2, S = 0.5 m）内流动轨迹如图4所示, 此时烟气入口速度为13 m/s, 可以看出灰尘颗粒在三维变形管管内受空气二次流的影响发生螺旋运动。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 灰尘颗粒轨迹（A/B = 2.2, S = 0.5 m）Fig. 4 Ash particle tracks (A/B = 2.2, S = 0.5 m)

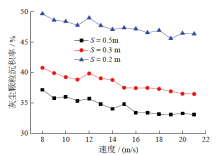
当入口灰尘粒径大小均为30 μ m时, 通过分析模型1、模型2和模型3的管内灰尘颗粒沉积率可以得出三维变形管的螺距S对灰尘颗粒的影响规律, 如图5所示。可以发现, 在管内气流流速为8 ~ 21 m/s的范围内, 灰尘颗粒沉积率随着螺距的减小而增大。如上文中所述, 流体在三维变形管管内流动时, 在垂直于主流方向上会发生二次流, 流体最终呈螺旋向前的流动。螺距越小, 说明三维变形管的扭曲变形越严重, 三维变形管管内的旋流将越显著, 随着螺旋离心力的增大, 当螺旋离心力对灰尘颗粒的影响大于重力对其影响时, 将有更多的灰尘颗粒与管内壁发生碰撞黏附, 最后附着于管壁上。

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 灰尘颗粒沉积率随螺距的变化Fig. 5 Variation of ash deposition rate with S

当入口灰尘粒径大小均为30 μ m时, 通过对三维变形管螺距对管内灰尘颗粒沉积率的影响分析可以总结出, 螺距越大, 管内积灰越少, 因此在讨论分析长短轴比A/B对三维变形管管内灰尘颗粒沉积率的影响时, 选取螺距较大的三维变形管作为研究对象, 以忽略螺距对灰尘颗粒沉积率的影响。通过分析模型1、模型4和模型5的管内灰尘颗粒沉积率可以得出三维变形管的长短轴比对灰尘颗粒沉积率的影响规律, 如图6所示, 可以发现在管内气流流速为8 ~ 21 m/s的速度范围内, 灰尘颗粒沉积率随着长短轴比的增大而增加。圆管经扭曲变形冷轧为三维变形管后, 管内体积缩小, 三维变形管长短轴比越大, 管内空气体积越小, 当含尘气流以同样的灰尘颗粒浓度流入三维变形管时, 随着三维变形管长短轴比的增大, 则灰尘颗粒与管壁碰撞、黏附的机会将增多, 管内壁灰尘颗粒沉积率自然增大。

图6

Fig. 6

	Figure Option ViewDownloadNew Window
	图6 灰尘颗粒沉积率随长短轴比的变化Fig. 6 Variation of ash deposition rate with A/B

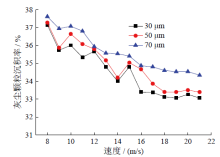
当三维变形管几何结构尺寸（A/B = 2.2, S = 0.5 m）不变, 而入口灰尘粒径分别为30 μ m、50 μ m和70 μ m时, 平均灰尘颗粒直径对沉积率的影响如图7所示。灰尘颗粒沉积率总体上呈现出随着平均灰尘颗粒直径增大而增加的趋势, 其主要原因在于:一方面, 灰尘颗粒的直径越大, 意味着其质量越大, 惯性越大, 速度冲量对其影响越小, 导致其越容易沉积; 另一方面, 当灰尘颗粒直径较小时, 灰尘颗粒所受惯性力较小, 重力对其起主要作用, 灰尘颗粒与管壁碰撞、黏附的概率较小, 而当平均灰尘颗粒直径增大时, 所受的惯性力将不断增大, 惯性力对灰尘颗粒的作用大于重力对其作用, 更多的灰尘颗粒与管壁发生碰撞黏附, 导致更多的灰尘颗粒沉积于三维变形管内壁面。

图7

Fig. 7

	Figure Option ViewDownloadNew Window
	图7 灰尘颗粒沉积率随平均灰尘颗粒直径的变化Fig. 7 Variation of ash deposition rate with average particle diameter

通过对图5、图6和图7的分析可知, 灰尘颗粒的灰沉积率随着空气流速的增大而减小, 但当空气流速大于15 m/s时, 灰尘颗粒沉积率的下降趋势减缓。当空气流速从8 m/s增大至15 m/s时, 粗灰颗粒对细灰颗粒沉积的侵蚀破坏作用变得越来越强, 灰尘颗粒沉积率下降, 然而当空气流速从15 m/s增大至21 m/s时, 灰尘颗粒的动能进一步增大, 细灰颗粒与管壁碰撞并黏附于管壁的几率增大, 沉积下来的灰尘颗粒数量增多, 粗灰颗粒对细灰沉积侵蚀破坏作用被削弱, 最终导致灰尘颗粒沉积率下降趋于平缓。