作者简介:文伟仲(1996-),男,硕士研究生,主要从事新能源发电电力电子控制相关技术研究。舒 杰(1969-),男,博士,研究员,主要从事可再生能源发电及微网技术研究。
CLLC谐振变换器因其可实现软开关、功率密度高、调压范围大等优点受到广泛关注,但其传统的控制方法存在开关频率变化大、软开关实现范围窄的不足,导致CLLC变换器效率和功率密度的进一步提高受限。针对上述问题,提出一种CLLC变换器的新型调频-扩展移相控制方法,将控制分为两段并给出了分段的边界条件,通过移相控制缩短了开关频率变化范围,通过增加原边和副边桥的移相角增大了软开关范围。基于基波模型分析了变换器的增益模型和软开关临界条件,并基于MATLAB进行多种控制方法下的对比试验,验证了所提控制方法的正确性和有效性。
CLLC resonant converter has been widely concerned because of its advantages such as soft switching, high power density and large output voltage range. However, its traditional control methods have disadvantages such as large switching frequency range and narrow soft switching realization range, which limited the further improvement of efficiency and power density of CLLC converter. To solve these problems, a novel frequency modulation-extended phase shift control method for CLLC converter was proposed. The control range was divided into two sections and boundary conditions are given. The range of frequency modulation was shortened by extended phase shift control, and the range of soft switching was increased by increasing the phase-shifting angle of the primary and secondary side bridges. The gain model and soft-switching critical condition of the converter were analyzed based on the first harmonic model, and the correctness and effectiveness of the proposed control method were verified by the comparative tests under various control methods based on MATLAB.
近年来, 应用在分布式可再生能源发电及其储能系统、新能源汽车、不间断电源等各种场合的双向DC/DC变换器(bidirectional DC/DC converter, BDC)越来越受到人们的关注和研究[1, 2], 随着电力电子技术的发展, 研究宽电压增益、高效、高功率的BDC具有重要意义。
针对传统BDC不适用于高压大功率场合的问题, 文献[3]研究了双有源桥电路(dual active bridge, DAB), 其具有电路结构简单, 原、副边电气隔离, 具备零电压软开关(zero voltage switching, ZVS)特性, 但是不能实现零电流软开关(zero current switching, ZCS), 且轻载会失去ZVS特性, 使得效率降低。文献[4]中的LLC谐振变换器可以实现ZVS及ZCS, 但是由于电路结构不对称, 在功率逆向传输时效率和电路特性很差。文献[2]提出的双向CLLC谐振变换器是基于原LLC变换器的拓扑优化, 其谐振回路结构完全对称, 故正、反向运行时的工作模态和性能均较好; 而且还具有软开关范围较宽、功率密度较大、调压范围宽等优势, 在高压、高频、大功率场合应用具有广阔的研究前景。
传统BDC的控制方法如脉冲频率调制[5](pulse frequency modulation, PFM)、脉冲宽度调制[6](pulse width modulation, PWM)、单移相控制[7](single phase shift, SPS)均可用于CLLC变换器。其中, PFM控制原理简单、软开关范围较宽, 但是在电压增益范围需求较宽的场合, 开关频率变化较大, 使变换器的整体效率降低; 而在SPS控制中, 开关频率为固定值, 但是电压增益的调节范围较窄, 且容易产生较大的回流功率。
为解决上述问题, 学者们进行了很多对于传统控制方法改进的研究。文献[8, 9]研究了扩展移相控制(extended phase shift, EPS), 在传统SPS控制的基础上增加了原边和副边两桥间的移相角, 并在LLC、CLLC拓扑上应用, 减小了回流功率, 提高了效率, 但是没有解决电压增益调节范围的问题; 文献[10] 提出了分段控制, 将整个调压范围分成PWM控制段和PFM控制段, 减小了开关频率变化范围, 同时也拥有较大的ZVS范围, 但是回流功率较大, 且应用在半桥LLC拓扑上, 没有对于全桥CLLC拓扑的研究。
基于上述研究, 本文提出了一种调频-扩展移相控制方法并应用于双向CLLC拓扑, 该控制方法在较高的电压增益时采用PFM控制, 在较低增益时采用EPS控制。对CLLC拓扑进行了分析, 相对于传统PFM控制和SPS控制, 本文提出的控制方法实现相同调压范围时开关频率变化范围窄, 软开关区间较大, 效率较高。然后进行了参数设计, 并利用MATLAB仿真验证了该方法的可行性及相对于传统控制方法的优势。
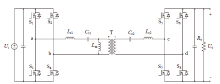
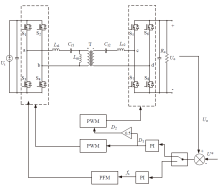
如图1为双向CLLC谐振变换器电路图, 由于拓扑的对称性, 以下的分析均针对功率由高压侧流向低压侧的情况, 反方向的分析不再赘述。Ui和Uo为输入和输出电压, 原边和副边的开关管分别为S1 ~ S4和S5 ~ S8, Lr1、Cr1和Lr2、Cr2分别为原边和副边谐振电感、电容, Lm为励磁电感, 变压器T的匝数比为n∶ 1。
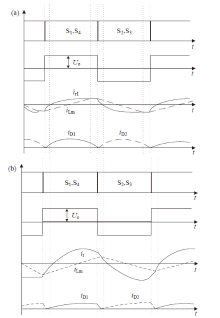
对于调频控制, 电路主要参数的波形图如图2所示, 基于开关频率fs和谐振频率fr的大小关系, 可以将变换器的工作模式分为两种, 其中${{f}_{\text{r}}}\text{=}\frac{1}{2\text{ }\!\!\pi\!\!\text{ }\sqrt{{{L}_{\text{r}1}}{{C}_{\text{r}1}}}}$。
fs ≤ fr时, 如图2a, 在一个开关周期内, 首先是Lr1和Cr1以fr为频率谐振, 而此时励磁电感两端电压被变压器副边电压钳位在固定值, 其电流为线性变化; 当励磁电流im与谐振电流ir1相等时, 变压器副边没有电流通过, Lm、Lr1和Cr1构成谐振回路, 共同谐振, 由于Lm远大于Lr1, 可以近似看作谐振电流的值较小且保持不变, 此时关断开关的电流较小; 当fs > fr时, 如图2b, ir1并未与im相等时闭合开关, 关断电流较大, 故在对于该拓扑的控制时, 应尽量保持开关频率小于或接近谐振频率。
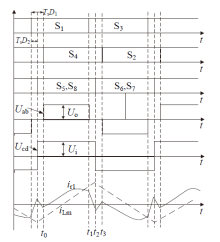
对于EPS控制, 波形图如图3所示, 原边两半桥臂的相移D1使原边谐振回路输入电压Uab方波的占空比减小, 即有效值减小; 原边和副边两桥开关之间的相移D2使副边输出电压Ucd方波的相位发生改变。
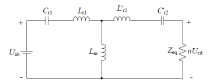
采用基波近似法(first harmonic approximation, FHA)分析, 图4为CLLC谐振变换器基波等效电路图, n为变压器的变比, Zeq为负载等效电阻, 从副边等效的L'r2= Lr2/n2、C'r2= n2Cr2, 为了保证谐振网络的对称性, 使其适用于能量双向流动, 一般设计参数使Lr1=L'r2、Cr1=C'r2。利用傅里叶级数计算谐振网络原边和副边电压的基波分量:
${{U}_{\text{ab}}}=\frac{4{{U}_{\text{i}}}\cos \left( {{D}_{1}}\text{ }\!\!\pi\!\!\text{ } \right)}{\text{ }\!\!\pi\!\!\text{ }}\sin \left( \omega t+{{\phi }_{\text{ab}}} \right)$ (1)
${{U}_{\text{cd}}}=\frac{4{{U}_{\text{o}}}}{\text{ }\!\!\pi\!\!\text{ }}\sin \left( \omega t+{{\phi }_{\text{cd}}} \right)$ (2)
式中:${{\phi }_{\text{ab}}}$= -D1π ; ${{\phi }_{\text{cd}}}$= -2D2π ; ω 为基波角速度。由式(1)、式(2)得基波分量有效值:
${{U}_{\text{ab }\!\!\_\!\!\text{ rms}}}\text{=}\frac{2\sqrt{2}{{U}_{\text{i}}}\cos \left( {{D}_{1}}\text{ }\!\!\pi\!\!\text{ } \right)}{\text{ }\!\!\pi\!\!\text{ }}$ (3)
${{U}_{\text{cd }\!\!\_\!\!\text{ rms}}}=\frac{2\sqrt{2}{{U}_{\text{o}}}}{\text{ }\!\!\pi\!\!\text{ }}$ (4)
由图4, 利用叠加定理得:
$\begin{align} & {{i}_{\text{r2}}}=-\frac{{{U}_{\text{ab}}}}{{{Z}_{1}}+{{Z}_{\text{m}}}//{{Z}_{2}}}\text{+}\frac{{{U}_{\text{cd}}}}{{{Z}_{1}}+{{Z}_{\text{m}}}//{{Z}_{2}}}\cdot \frac{{{Z}_{\text{m}}}}{{{Z}_{\text{m}}}+{{Z}_{2}}} \\ & \text{ =}{{X}_{i\text{r2}}}+j{{Y}_{i\text{r2}}} \\ \end{align}$ (5)
由式(5)可得ir2的相位角和有效值分别为:
${{\phi }_{i\text{r2}}}=\arctan \left( \frac{{{Y}_{i\text{r2}}}}{{{X}_{i\text{r2}}}} \right)$ (6)
${{I}_{\text{r2 }\!\!\_\!\!\text{ rms}}}=\left\| {{i}_{\text{r2}}} \right\|$ (7)
可求得Zeq的阻抗角为:
${{\phi }_{Z\text{eq}}}={{\phi }_{\text{cd}}}-{{\phi }_{i\text{r2}}}$ (8)
负载等效阻抗Zeq的模值[8]:
$\left\| {{Z}_{\text{eq}}} \right\|=\frac{n{{U}_{\text{r2 }\!\!\_\!\!\text{ rms}}}}{{{I}_{\text{r2 }\!\!\_\!\!\text{ rms}}}/n}\text{=}\frac{8{{n}^{2}}{{R}_{\text{o}}}\cos {{\phi }_{Z\text{eq}}}}{{{\text{ }\!\!\pi\!\!\text{ }}^{2}}}$ (9)
则Zeq可以表示为:
${{Z}_{\text{eq}}}\text{=}\left\| {{Z}_{\text{eq}}} \right\|\angle {{\phi }_{{{Z}_{\text{eq}}}}}={{Z}_{\text{eq}}}\left( \cos {{\phi }_{{{Z}_{\text{eq}}}}}+j\sin {{\phi }_{{{Z}_{\text{eq}}}}} \right)$ (10)
由图4得谐振网络传递函数为:
$\left\| H \right\|=\frac{n{{U}_{\text{cd }\!\!\_\!\!\text{ rms}}}}{{{U}_{\text{ab }\!\!\_\!\!\text{ rms}}}}=\left\| \frac{{{Z}_{\text{m}}}//\left( {{Z}_{2}}+{{Z}_{\text{eq}}} \right)}{{{Z}_{1}}+{{Z}_{\text{m}}}//\left( {{Z}_{2}}+{{R}_{\text{eq}}} \right)}\cdot \frac{{{Z}_{\text{eq}}}}{{{Z}_{2}}+{{Z}_{\text{eq}}}} \right\|$ (11)
式中:Zm为励磁阻抗, Zm= jω Lm; Z1为原边谐振阻抗, Z1= jω Lr1+ 1/(jω Cr1); Z2为副边谐振阻抗, Z2= jω Lr2+ 1/(jω Cr2); k为变压器励磁电感与谐振电感之比, k = Lm/Lr1; Q为CLLC电路的品质因数, Q = (Lr1/Cr1)0.5/Zeq; fn为归一化频率, fn = fs/fr。
电压增益:
${{G}_{\text{EPS}}}=\frac{n{{U}_{\text{o}}}}{{{U}_{\text{i}}}}=\left\| H \right\|\cdot \cos \left( {{D}_{1}}\text{ }\!\!\pi\!\!\text{ } \right)$ (12)
采用同样的方法可以得到调频控制[11]和传统移相控制的电压增益分别为:
$\begin{align} & {{G}_{\text{PFM}}}=\left\| {{H}_{1}} \right\| \\ & =\frac{1}{\sqrt{{{\left( \frac{Q}{k} \right)}^{2}}{{\left[ \left( 2k+1 \right){{f}_{\text{n}}}-\frac{2k+2}{{{f}_{\text{n}}}}+\frac{1}{f_{\text{n}}^{3}} \right]}^{2}}+{{\left( 1+\frac{1}{k}-\frac{1}{k{{f}_{\text{n}}}^{2}} \right)}^{2}}}} \\ \end{align}$(13)
${{G}_{\text{PS}}}=\left\| {{H}_{1}} \right\|\cdot \cos \left( {{D}_{1}}\text{ }\!\!\pi\!\!\text{ } \right)$ (14)
由于两种控制方法中, Zeq为纯电阻故可表示为Req, Req= 8n2Ro/π 2, 此时Q = (Lr1/Cr1)0.5/Req。
运行中CLLC谐振变换器的损耗Ploss主要由开关损耗Psw、变压器损耗Ptra和谐振回路损耗PLC组成。其中, Ptra和PLC主要为磁芯损耗, 与变换器的参数有关; Psw主要由导通损耗Pcond、开关的通断损耗Pon/off, 在保证开关ZVS的情况下, 可近似认为Pon/off很小且与D1、D2无关[12]。
对于开关管的导通损耗:
${{P}_{\text{cond}}}=2I_{\text{r1 }\!\!\_\!\!\text{ rms}}^{\text{2}}{{R}_{\text{dson}}}+2I_{\text{r2 }\!\!\_\!\!\text{ rms}}^{\text{2}}{{R}_{\text{dson}}}$ (15)
式中:Ir1_rms、Ir2_rms为原边和副边谐振电流的有效值, Rdson为开关管的导通电阻。
由图4, 利用叠加定理得:
${{i}_{\text{r}1}}=\frac{{{U}_{\text{ab}}}}{{{Z}_{1}}+{{Z}_{\text{m}}}//{{Z}_{2}}}-\frac{{{U}_{\text{cd}}}}{{{Z}_{1}}+{{Z}_{\text{m}}}//{{Z}_{2}}}\cdot \frac{{{Z}_{\text{m}}}}{{{Z}_{\text{m}}}+{{Z}_{1}}}$ (16)
由式(5)和式(16)可得Ir1_rms和Ir2_rms的表达式, 再代入式(15)可求得Pcond。
提出一种调频-扩展移相控制应用于CLLC拓扑, 这种控制方法的优势是相对于传统PFM控制, 实现相同的电压增益时开关频率变化范围较窄, EPS控制部分相对于单移项控制可以减小开关管的导通损耗, 提高变换器的效率。
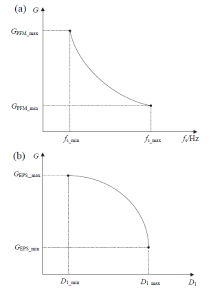
所提出的控制方法框图如图5。控制分为两段, 如图6所示, 在负载相同的情况下, 较高的电压增益采用PFM控制模式:电压增益范围为GPFM_max≥ G ≥ GPFM_min, 开关频率变化范围为fs_min≤ fs≤ fs_max; 较低的电压增益采用EPS控制模式:文献[9]通过实验验证, 得到D2= 0.5D1使ir1_rms和ir2_rms最小的结论, 在其余损耗不变的情况下开通损耗有最小值, 即变换器的效率最高。为保证变压器的效率, 保持D2= 0.5D1, 将D1视作单独未知数控制电压增益, 也便于参数设计, 增益范围为GEPS_max≥ G ≥ GEPS_min, 移相范围为D1_min≤ D1≤ D1_max。
分段控制的边界条件:调频控制中fs_min对应的电压增益GPFM_max为变压器可达到的最大增益, 由工况决定, fs-G的关系式为式(13); fs_max对应的电压增益GPFM_min= GEPS_max为两端控制的分界点, 此时D1= D1_min= 0; EPS控制中D1_max对应的电压增益GEPS_min也由工况决定, D1-G的关系式为式(12), 此时开关工作频率为fs_min。
通过式(12)和式(14)可得, 基于FHA分析, EPS控制与传统移相控制的电压增益表达式相同, 在开关频率fs一定时仅以相移D1为变量, 且D1的增大使相同fs时相对调频控制的电压增益减小, 即相对于调频控制, 实现相同的开关增益, 调频-扩展移相控制的fs变化范围更窄, 开关关断电流和谐振损耗更小。
对于原边侧开关, 开关管的电流滞后于开关电压方波的上升沿时, 可保证ZVS。原边输入阻抗为:
${{Z}_{\text{in}}}={{Z}_{1}}+{{Z}_{\text{m}}}//\left( {{Z}_{2}}+{{Z}_{\text{eq}}} \right)$ (17)
令Zin= X + jY, 则输入阻抗角${{\phi }_{Z\text{in}}}=\arctan \left( {Y}/{X}\; \right)$ , 为了保证ZVS, 有:
${{\phi }_{i\text{r2}}}\text{=}{{\phi }_{{{Z}_{\text{in}}}}}+{{\phi }_{\text{ab}}}\ge 2\text{ }\!\!\pi\!\!\text{ }{{D}_{1}}$ (18)
为了实现较小的fs变化范围, 需要将EPS控制实现的电压增益范围取得尽量大, 即取临界状态${{\phi }_{Z\text{in}}}\text{+}{{\phi }_{\text{ab}}}\text{=2 }\!\!\pi\!\!\text{ }{{\text{D}}_{\text{1}}}$ 时对应的fs和D1分别作为fs_max和D1_max, 联立式(12)可求得fs_max、D1_max以及G = GPFM_min= GEPS_max的值。
原边谐振电流ir1的相位如式(16), 代入不同参数可知, 在D1不变的情况下, 增大D2的值, 可以增大原边开关管两端电流的相值, 即相对于SPS控制, EPS控制模式下的软开关区间更大, 在软开关区间内可以实现的电压增益更大。
利用MATLAB中Simulink模块对上述分析的结果进行仿真验证, 设计一个额定功率为3 kW的CLLC变换器, 其额定输出电压Uo为200 V, 输入电压控制在333 ~ 500 V范围内, 电压增益G范围为0.8 ~ 1.2。
在参数设计时:设定谐振频率为100 kHz; 根据额定电压得变压器的变比n = 2; 设计k值和Q值, 保证在PFM控制段, 其电压增益表达式(13)的曲线在额定增益区间内保持单调递减, 有利于控制电路的设计。根据k、Q可以得到谐振回路的参数如表1。
| 表1 仿真参数 Table 1 Simulation parameters |
将参数代入式(12)、式(18)求得分段控制的边界条件:PFM段中51.6 kHz ≤ fs≤ 100 kHz, 1 ≤ G ≤ 1.2; EPS段中0 ≤ D1= 2D2≤ 0.2, 0.8 ≤ G ≤ 1。
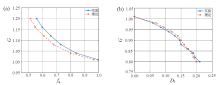
利用上述参数进行仿真, 图7为全增益范围内调频-扩展移相控制下的G-fn、D1曲线, 由图可知, 仿真数据与理论数据之间误差较小。
图8a为额定负载下输出电压波形, 稳态下输出电压较平稳; 图8b为原边谐振电流ir1与原边输入电压Uab波形, ir1的过零点滞后于开关开通时电压波形的上升沿; 图8c为开关管S1漏源电压US1和通过S1电流iS1的波形, 此时处于临界状态, 开关管两端电压降至0的时刻开关导通, 实现了ZVS。
 | 图8 (a)输出电压Uo波形; (b)谐振电流ir1与输入电压Uab波形; (c)US1和iS1波形Fig. 8 (a) Output voltage curve; (b) curves of resonance current and input voltage; (c) curves of US1 and iS1 |
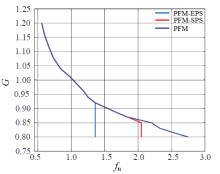
图9为调频-扩展移相控制与传统PFM控制及PFM-SPS控制的G-fn图像, 实现相同的电压增益0.8 ~ 1.2, PFM控制的开关频率范围为56 kHz ~ 275 kHz, PFM-SPS控制的开关频率范围为56 kHz ~ 205 kHz, 调频-扩展移相控制的开关频率范围为56 kHz ~ 96.5 kHz, 相对于前两种方法有明显优势。
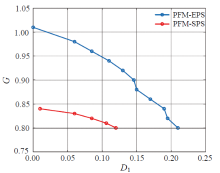
图10为调频-扩展移相控制与PFM-SPS控制中移相控制段G-D1曲线, D2的取值在前者中为0.5D1, 在后者中为0。由于两种方法均将ZVS临界状态作为边界值, 在保证ZVS的情况下调频-扩展移相控制中相移调节范围更大, 且实现更宽的增益范围, 使其PFM控制段开关频率变化范围更小, 效率更高。
针对双向CLLC谐振变换器的现有控制方法进行了分析, 为了解决传统PFM和SPS控制方法存在的开关频率变化较大, 软开关范围较小等问题, 提出了一种新型的调频-扩展移相控制方法, 将额定增益区间分为两段, 较高的增益段采用PFM控制, 较低的增益段采用EPS控制, 将传统控制方法的优势整合到一起。
对于新型分段控制方法进行了FHA建模分析, 推导了PFM段和EPS段的增益表达式、分析了该控制方法下的软开关范围并将ZVS临界条件作为控制段边界条件、分析了变换器的损耗情况。主要结论如下:
(1)提出的控制方法结合了传统控制方法的优势, 解决了单一传统控制方法的不足, 在PFM段收窄了增益变化范围, 频率变化更小, 在EPS控制段比传统SPS控制的软开关范围更大、增益区间也更宽。
(2)针对提出的分段控制方法, 基于MATLAB仿真平台对3 kW变换器的参数设计算例进行了数字建模仿真。仿真结果显示, 当电压增益范围为0.8 ~ 1.2时, 与采用传统PFM控制、PFM-SPS控制方法相比, 采用本文所提出控制方法的开关频率变化范围显著减小, 该算例验证了本文对于调频-扩展移相分段控制的分析。
综上, 本文提出的控制方法在减少开关频率变化范围、提高变换器的效率两方面优于传统的CLLC控制方法, 对双向DC/DC变换器提高功率密度及效率有着较优效果, 有助于高效高功率密度双向DC/DC变换器在分布式新能源发电及分布式储能上的推广应用。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|