各个截面上水和二氧化碳遵循质量和能量守恒^{[15, 17]}（以下公式中的符号含义见文后的符号表）：

$\frac{\mathrm{d} M_{\mathrm{t}}}{\mathrm{d} L}=0$ (2)

液相中二氧化碳的溶解浓度按亨利定律给出, 气相中二氧化碳的含量由分压确定^[18]：

$n_{1}=\alpha(T) P_{\mathrm{c}}$ (3)

$n_{\mathrm{g}}=\frac{44 P_{\mathrm{c}}}{44 P_{\mathrm{c}}+18 P_{\mathrm{w}}}$ (4)

式（3）中的系数根据文献[19]计算确定。

在闪蒸点, 流体的总压等于二氧化碳的分压与流体温度对应的饱和水蒸气压力之和^[17]：

$P_{\mathrm{t}}=P_{\mathrm{c}}+P_{\mathrm{w}}$ (5)

$P_{\mathrm{wtb}}=P_{\mathrm{w}}+\frac{n_{1}}{\alpha(T)}$ (6)

流体的干度以及各项流量由下式给出^[17]：

$x_{\mathrm{s}}=\frac{H_{\mathrm{wt}}-H_{\mathrm{w}}}{H_{\mathrm{s}}-H_{\mathrm{w}}}$ (7)

$M_{\mathrm{wt}}=M_{\mathrm{t}}(1-\gamma)$ (8)

$M_{\mathrm{s}}=M_{\mathrm{wt}} x_{\mathrm{s}}$ (9)

$M_{\mathrm{w}}=M_{\mathrm{wt}}\left(1-x_{\mathrm{s}}\right)$ (10)

$M_{\mathrm{ct}}=M_{\mathrm{t}} \gamma$ (11)

$M_{\mathrm{gc}}=\frac{n_{\mathrm{g}} M_{\mathrm{s}}}{1-n_{\mathrm{g}}}$ (12)

$M_{\mathrm{lc}}=\frac{n_{1} M_{\mathrm{w}}}{1-n_{1}}$ (13)

地热井运行一段时间后, 流体向井筒周围岩石的传热基本达到平衡, 相对于井口采出的热量, 通过井筒向围岩散热造成的热损失很小, 在计算时忽略不计。对于二氧化碳含量一定的地热流体, 在各个不同深度的截面上气液相的总焓值相等^[15]。

$\begin{aligned}G(\gamma, P, T)=& \frac{n_{1}-\gamma}{n_{\mathrm{g}}-n_{1}}\left[n_{\mathrm{g}} H_{\mathrm{gc}}+\left(1-n_{\mathrm{g}}\right) H_{\mathrm{gw}}\right]+\\& \frac{\gamma-n_{\mathrm{g}}}{n_{\mathrm{g}}-n_{1}}\left[n_{1} H_{1 \mathrm{c}}+\left(1-n_{1}\right) H_{1 \mathrm{w}}\right]\end{aligned}$ (14)

$G(\gamma, P, T)=\text { constant }=G\left(\gamma, P_{0}, T_{0}\right)$ (15)

在流体闪蒸之前为单相流, 压力损失主要包括重力造成的压降、摩擦压降和加速压降。由于不考虑通过井筒的热量损失, 在闪蒸发生前, 流体的温度不变, 式（18）中流体的比容是不变的^{[20, 21]}。

$\Delta P_{\mathrm{t}}-\left(\Delta P_{\mathrm{a}}+\Delta P_{\mathrm{g}}+\Delta P_{\mathrm{f}}\right)=0$ (16)

$\Delta P_{\mathrm{g}}=\rho g \Delta L$ (17)

$\Delta P_{\mathrm{a}}=\left(\frac{M_{\mathrm{t}}}{A}\right)^{2}\left(v_{1}-v_{2}\right)$ (18)

$\Delta P_{\mathrm{f}}=\frac{\lambda \Delta L}{2 D \rho}\left(\frac{M_{\mathrm{t}}}{A}\right)^{2}$ (19)

总的体积流量：

$Q_{\mathrm{t}}=Q_{\mathrm{g}}+Q_{1}$ (20)

$V_{\mathrm{t}}=\frac{Q_{\mathrm{t}}}{A}$ (21)

流型判断参数^{[20, 21]}：

$V_{\mathrm{gd}}=\frac{Q_{\mathrm{g}}}{A \sqrt[4]{\frac{\rho_{1}}{g \sigma}}}$ (22)

$L_{\mathrm{B}}=1.071-0.7277 \frac{V_{\mathrm{t}}^{2}}{D}$ (23)

式中：L_B— bubble-slug转变边界, 无量纲, L_B ≥ 0.13。

$L_{\mathrm{S}}=50+36 V_{\mathrm{gd}} \frac{Q_{1}}{Q_{\mathrm{g}}}$ (24)

式中：L_S— slug-transition转变边界, 无量纲。

$L_{\mathrm{M}}=75+84\left(V_{\mathrm{gd}} \frac{Q_{1}}{Q_{\mathrm{g}}}\right)^{0.75}$ (25)

式中：L_M— transition-mist转变边界, 无量纲。

流型判断准则：

$ \frac{Q_{\mathrm{g}}}{Q_{\mathrm{t}}}< L_{\mathrm{B}} bubble $ (26)

$ \left.\begin{array}{l}\frac{Q_{\mathrm{g}}}{Q_{\mathrm{t}}}> L_{\mathrm{B}} \\V_{\mathrm{gd}}< L_{\mathrm{S}}\end{array}\right\} slug $ (27)

$ L_{\mathrm{S}}< V_{\mathrm{gd}}< L_{\mathrm{M}} transition $ (28)

$ V_{\mathrm{gd}}> L_{\mathrm{M}} mist $ (29)

假如流型是bubble, 按如下公式计算

$F_{\mathrm{g}}=\frac{1}{2}\left[1+\frac{Q_{\mathrm{t}}}{V_{\mathrm{s}} A}-\sqrt{\left(1+\frac{Q_{\mathrm{t}}}{V_{\mathrm{s}} A}\right)^{2}-\frac{4 Q_{\mathrm{g}}}{V_{\mathrm{s}} A}}\right]$ (30)

$\bar{\rho}=\left(1-F_{\mathrm{g}}\right) \rho_{1}+F_{\mathrm{g}} \rho_{\mathrm{g}}$ (31)

$\tau_{\mathrm{f}}=\lambda \rho_{1} \frac{u_{1}^{2}}{2 D}$ (32)

$u_{1}=\frac{Q_{1}}{A_{1}}=\frac{Q_{1}}{A\left(1-F_{\mathrm{g}}\right)}$ (33)

假如流型是slug, 按如下公式计算：

$R e=\frac{\rho_{1} V_{\mathrm{t}} D}{\mu_{1}}$ (34)

$R e_{\mathrm{b}}=\frac{\rho_{1} V_{\mathrm{b}} D}{\mu_{1}}$ (35)

假如$R e_{\mathrm{b}} \leq 3000$

$V_{\mathrm{b}}=\left(0.546+8.74 \times 10^{-6} \operatorname{Re}\right) \sqrt{g D}$ (36)

假如$3000< R e_{\mathrm{b}}< 8000$

$V_{\mathrm{bi}}=\left(0.251+8.74 \times 10^{-6} \mathrm{Re}\right) \sqrt{g D}$ (37)

$V_{\mathrm{b}}=\frac{1}{2}\left(V_{\mathrm{b} \mathrm{i}}+\sqrt{V_{\mathrm{bi}}^{2}+\frac{11170 \mu_{1}}{\rho_{1} \sqrt{D}}}\right)$ (38)

假如$N_{\mathrm{b}} \geq 8000$

$V_{\mathrm{b}}=\left(0.35+8.74 \times 10^{-6} \operatorname{Re}\right) \sqrt{g D}$ (39)

$\bar{\rho}=\frac{M_{\mathrm{t}}+\rho_{1} A V_{\mathrm{b}}}{Q_{\mathrm{t}}+A V_{\mathrm{b}}}+\Gamma \rho_{1}$ (40)

$\tau_{\mathrm{f}}=\frac{\lambda \rho_{1} u_{\mathrm{t}}^{2}}{2 D}\left(\frac{Q_{1}+A V_{\mathrm{b}}}{Q_{\mathrm{t}}+A V_{\mathrm{b}}}+\Gamma\right)$ (41)

两个截面之间的压力损失为：

$\Delta P=\left(\frac{\bar{\rho} g+\tau_{\mathrm{f}}}{1-\frac{M_{\mathrm{t}} Q_{\mathrm{g}}}{A^{2} \bar{P}}}\right) \Delta L$ (42)

上述方程有两种求解方法, 一是已知井底参数（压力、温度、总质量流量、二氧化碳含量）, 由井底逐步向井口方向求解, 确定各个截面的参数, 称为Down-Top算法^[20]; 二是已知井口参数（压力、温度、干度、总流量、二氧化碳含量）, 由井口逐步向井底和热储方向求解, 称为Top-Down。本文以Down-Top算法为例, 简要介绍求解方法。

（1）根据井筒长度L, 将井筒从上到下等距离分成若干份, 每份长度Δ L;

（2）根据流体温度计算水蒸气饱和蒸汽压, 再根据式（3）, 已知二氧化碳含量计算其分压;

（3）根据式（6）计算闪蒸开始的压力;

（4）根据式（16）~ 式（19）, 计算从井底到闪蒸点的距离, 确定闪蒸位置;

（5）对于两相流压降的计算, 首先假设下一点的压力, 根据假设的压力, 通过式（14）和式（15）求解该点的温度;

（6）待温度求解平衡后, 根据温度和假设的压力, 利用式（7）~ 式（13）, 更新干度和各相的流量以及物性;

（7）根据两相流的判定准则以及压降计算公式, 计算假设点的压力;

（8）比较假设压力和计算的压力, 如果偏差小于设定值, 进入下一点继续计算; 如果大于设定值, 继续计算, 直至满足要求;

（9）输出各个截面的压力、温度、干度、流量等参数。

如果是已知井口参数, 计算步骤与上述类似, 先从井口判断两相流流型, 确定压降, 逐步向下计算到单相流和闪蒸点。

文献[17]中, 在二氧化碳质量含量为0.5%时, 其计算的闪蒸位置为1 270 m, 用到的参数如表1所示。根据表1的数据, 按照1.4节的方法求解方程, 计算得到的闪蒸位置为1 257 m, 与文献[17]的相对误差为1.02%。

表1

Table 1

表1(Table 1)

表1 计算参数表 Table 1 Parameter list used for calculation 参数 单位 数值 井底压力 bar 75 井底温度 ℃ 260 质量流量 kg/s 50 井筒直径 m 0.2 井深 m 1 500 井管表面粗糙度 m 4.6× 10-5 二氧化碳质量含量 % 0.5

表1 计算参数表 Table 1 Parameter list used for calculation

热储的下降因子由下式计算：

$ C_{\mathrm{D}}=\frac{P_{\mathrm{R}}-P_{\mathrm{wb}}}{M}$ (43)

下降因子是热储的固有特性, 可以通过两个稳态流动工况进行确定：调节井口压力分别为P_wh1和P_wh2, 待系统流动平衡后, 对应的流量和井底压力分别为M₁、M₂和P_wb1、P_wb2。根据井口成分和上述两相流理论, 通过井口压力可以计算出对应的井底压力。则有：

$ C_{\mathrm{D}}=\frac{P_{\mathrm{R}}-P_{\mathrm{wb} 1}}{M_{1}}$ (44)

$ C_{\mathrm{D}}=\frac{P_{\mathrm{R}}-P_{\mathrm{wb} 2}}{M_{2}}$ (45)

整理上述方程可得：

$ C_{\mathrm{D}}=\frac{P_{\mathrm{wb} 2}-P_{\mathrm{wbl}}}{M_{1}-M_{2}}$ (46)

$ P_{\mathrm{R}}=\frac{M_{2} P_{\mathrm{wb} 1}-M_{1} P_{\mathrm{wb} 2}}{M_{2}-M_{1}}$ (47)

式（46）和式（47）中井底压力可由井口压力计算获得, 因此, 可以通过井口的压力和流量计算下降因子和热储压力。另外, 下降因子由下述参数确定：

$ C_{\mathrm{D}}=\frac{\mu_{\mathrm{R}} \ln \left(\frac{r_{\mathrm{R}}}{r_{\mathrm{W}}}\right)}{2 \pi K L_{\mathrm{R}} \rho_{\mathrm{R}}}$ (48)

上述下降因子的表达式中, 仅有热储渗透率、热储厚度和半径未知。因此, 测出三个参数中的两个, 可以求解另一个, 或者测出一个, 可以求出另两个的组合值。在不同的年份计算多个稳态工况下的下降因子和热储压力, 可以画出二者随时间的变化规律, 以此判断热储的衰减程度和后续开采能力。

质量流量和井口压力关系密切, 如图1a所示。当井口压力逐渐调大时, 质量流量逐渐减小。当质量流量减小到180 t/h时, 井口压力出现最大值5.28 bar。再继续减小流量, 井口压力不但没增大反而减小了, 这与文献[20]中的模拟趋势是一致的。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 （a）质量流量与井口压力的关系; （b）质量流量与闪蒸深度的关系; （c）井口温度、二氧化碳分压和干度与质量流量的关系Fig. 1 (a) Relationship between mass flow rate and wellhead pressure; (b) variation of flashing depth with mass flow rate; (c) variation of wellhead temperature, CO2partial pressure and dryness with mass flow rate

质量流量和闪蒸深度的关系见图1b。由图1b可知, 随着质量流量的增大, 闪蒸深度逐渐变大。由于热储的下降因子不变, 增大质量流量, 导致井底的压力变小。在井筒内从井底向上的流动过程中, 摩擦阻力也随着流量的增大而增大。因此, 在流体温度和二氧化碳含量不变的情况下, 闪蒸点的压力是不变的, 而流体的压力损失随流量而增大, 导致闪蒸提早发生, 因此出现闪蒸点随流量增加而下移的规律。实际工程中, 结垢位置发生在闪蒸位置以上, 阻垢剂的加注一般在闪蒸位置以下100 m, 因此, 确定闪蒸位置至关重要。

由图1a的分析可知, 当流量大于180 t/h时, 井口压力随流量增大而减小。在热储温度和二氧化碳含量不变的情况下, 井口压力越小, 导致越多的液体水闪蒸为水蒸气, 致使井口干度增大、温度降低和二氧化碳分压减小, 如图1c所示。

图2反映了在质量流量为200 t/h时, 流体温度、干度和压力随深度的变化。由于热储压力和下降因子不变, 当流量不变时, 井底压力也保持恒定。在流体从井底向井口流动的过程中, 在未闪蒸前, 流体温度不变, 压力损失主要是重力和摩擦引起的。由图2a可知, 从井底3 000 m深度, 到闪蒸点深度794 m, 流体压力线性降低, 流体温度保持不变。在闪蒸点, 流体总压小于二氧化碳分压与流体温度对应的饱和水蒸气压力之和, 出现闪蒸汽化现象。在闪蒸点附近, 流体温度和压力均出现较大变化：由于闪蒸汽化吸热, 流体温度突然降低; 由于气相密度降低, 流体压降梯度较单相流变小, 如图2a所示。自闪蒸点开始, 流体从单相流进入两相流, 流体的压力损失按照两相流计算。图2b中, 流体的干度从闪蒸点到井口逐渐增加, 越向上, 干度随深度的变化梯度越大, 这说明越向上, 液体闪蒸为气体的量越大。液体闪蒸为气体的量越大, 流体温度降低也越大, 从图2a和图2c可知, 干度变化和温度变化的斜率是一致的。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 （a）流体压力和温度随深度的变化; （b）流体干度随深度的变化; （c）总压、分压和温度随深度的变化Fig. 2 (a) Variation of pressure and temperature with depth; (b) variation of dryness with depth; (c) variation of total pressure, partial pressure and temperature with depth

地热水因溶解了CO₂而具有侵蚀性, 能在热储中和固态碳酸钙岩发生溶蚀作用。同样, 在地热流体运移过程中, 由于压力减小（地热流体从热储开采到地面, 温度是逐渐降低的, 而温度的降低能促进碳酸钙的溶解, 在本文中暂不考虑温度降低对碳酸钙结垢的影响）, CO₂从液相逸出, 造成了碳酸钙结垢。因此, 研究CO₂含量对流动和结垢的影响具有重要的意义。

CO₂含量增加, 在温度不变的情况下, 气相二氧化碳分压增大, 闪蒸点压力变大。当热储压力、下降因子和流量不变时, CO₂含量大时, 热储压力与闪蒸点压力的差就变小, 即可供消耗的压损小。在单相流体流动时, 重力压损和摩擦压损超过可供消耗的压损就会发生闪蒸。因此可以得出CO₂含量越大闪蒸深度也越大的结论, 如图3a所示。由图3a和图3b中井口干度和温度的变化趋势可知, 二者变化趋势相反, 但恰恰符合变化规律。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 （a）CO2质量含量对井口干度和闪蒸深度的影响; （b）CO2质量含量对井口温度、压力和二氧化碳分压的影响; （c）不同CO2含量条件下, 流体温度随深度的变化Fig. 3 (a) Effect of CO2 content on wellhead dryness and flashing depth; (b) effect of CO2 content on wellhead temperature, pressure and CO2 partial pressure; (c) variation of temperature with depth and CO2 content

图3c反映了不同二氧化碳含量时, 流体温度随深度的变化, 仅仅画出了闪蒸点以后的变化趋势。从图3c可知, 二氧化碳含量低时, 井口温度也低, 说明液相地热水的汽化量大, 干度大, 这与图3a和图3b的结论一致。

由图4a可知, 热储温度对井口压力和井口温度有较大影响, 二者均随热储温度的升高而增大。闪蒸深度受热储温度的影响较小, 当热储温度在90 ~ 150℃之间变化时, 闪蒸深度在790 m附近变化不大。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 （a）井口温度、压力和闪蒸深度与热储温度的关系; （b）井口压力和CO2分压与热储压力的关系; （c）热储压力对井口干度、温度和闪蒸深度的影响Fig. 4 (a) Variation of wellhead temperature, pressure and flashing depth with reservoir temperature; (b) relationship of wellhead pressure and CO2 partial pressure with reservoir pressure; (c) effect of reservoir pressure on wellhead dryness, temperature and flashing depth

由图4b和图4c可知, 随热储压力的增加, 井口流体总压和二氧化碳分压均增加, 而闪蒸深度变浅, 井口温度升高。由于流体温度和二氧化碳含量不变, 闪蒸压力保持不变。从热储到闪蒸点之间的压损, 随热储压力的增大而增大。对单相流而言, 在温度和流量不变的情况下, 压损大代表流体流过的竖直高度大, 闪蒸深度变浅。

由图5a可知, 管壁粗糙度越大, 闪蒸深度越大, 井口压力越小。这是由于在热储压力、温度、流量和二氧化碳含量不变的工况下, 闪蒸点压力也不变, 管壁粗糙度越大, 压损越大, 越容易到达闪蒸压力。不论是对于单相流还是两相流, 管壁越粗糙, 摩擦阻力越大, 导致井口压力越小。井口压力的减小致使更多的液相地热水汽化到气相, 导致井口干度增加, 井口温度降低, 如图5b所示。

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 （a）井口压力和闪蒸深度与井管表面粗糙度的关系; （b）井口温度和干度与井管表面粗糙度的关系Fig. 5 (a) Relationship of wellhead pressure and flashing depth with the surface roughness of well tube; (b) relationship of wellhead temperature and dryness with the surface roughness of well tube

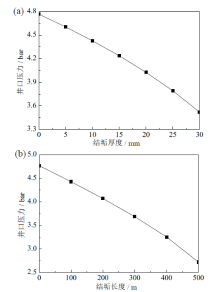
研究了两种工况下结垢对流动的影响：一种是结垢从闪蒸点开始延续长度100 m, 结垢厚度从0 mm到30 mm变化; 另一种是结垢厚度为10 mm, 结垢从闪蒸点开始延续长度从0 m到500 m变化。从图6a可知, 在结垢延续长度不变的工况下, 随着结垢厚度的增加, 井口压力降低。这是由于结垢厚度越大, 井管流通面积越小, 其流速越大, 导致摩擦压降增加。图6b说明, 在结垢厚度不变的工况, 结垢延续长度越大, 井口压力越小。下一步, 本课题组将重点研究结垢厚度和长度对流量和生产的影响。

图6

Fig. 6

	Figure Option ViewDownloadNew Window
	图6 （a）结垢厚度对井口压力的影响; （b）结垢长度对井口压力的影响Fig. 6 (a) Effect of scale thickness on wellhead pressure; (b) effect of scale length on wellhead pressure