引用本文
樊苗苗, 顾涛, 李念思, 余本东. 光热复合催化Trombe墙性能及百叶角度调控策略研究[J]. 新能源进展, 2024,12(1): 40-47
FAN Miaomiao, GU Tao, LI Niansi, YU Bendong. Performance Analysis of the Photo-Thermal Composite Catalytic Trombe Wall and the Angle Control Strategy of Blinds[J]. ADV NEW RENEWABLE EN, 2024,12(1): 40-47.  
Doi: 10.3969/j.issn.2095-560X.2024.01.005
Permissions
Copyright©2024, 《新能源进展》编辑部
版权所有 © 《新能源进展》编辑部
光热复合催化Trombe墙性能及百叶角度调控策略研究
樊苗苗1,2, 顾涛2, 李念思2, 余本东1,2,†
1.安徽建筑大学,建筑能效控制与评估教育部工程研究中心,合肥 230601
2.南京工业大学 城市建设学院,南京 210009
†通信作者：余本东,E-mail：yubendonglns@163.com

作者简介：樊苗苗（1998-）,女,硕士研究生,主要从事太阳能光热催化洁净与建筑一体化技术研究。余本东（1991-）,男,博士,教授,主要从事太阳能光电光热综合利用研究。

收稿日期: 2023-07-10 修订日期: 2023-09-13
基金项目: 建筑能效控制与评估教育部工程研究中心开放课题/主任基金资助项目（AHJZJN-2021-03）; 江苏省自然科学面上基金项目（BK20221315）; 国家自然科学基金项目（52238004,52278111）
摘要

太阳能热催化技术利用太阳全光谱产生集热和降解甲醛,太阳能光热复合催化技术是一种可以同时利用光和热产生热量并降解甲醛的高效技术。分别将热催化、光热复合催化百叶技术应用到Trombe墙系统,实现采暖的同时,能够利用太阳光降解室内气态污染物。建立热催化、光热复合催化百叶Trombe墙传热传质模型并进行实验验证,基于模型探究热催化百叶Trombe墙和光热复合催化百叶Trombe墙在南京和北京冬至日（9:00—17:00）气象参数下百叶全天最佳调控策略。结果表明,建立的传热传质模型预测与实验数据符合度较高。同一百叶Trombe墙系统,不同地区的最佳百叶角度不同;对于热催化百叶Trombe墙,南京全天最佳百叶角度下,产生的热量和干净空气量分别为5.6 MJ/d、196.7 m3/d,北京分别为4.6 MJ/d、167.9 m3/d;对于光热复合催化百叶Trombe墙,南京全天最佳百叶角度下,产生的热量和干净空气量分别为6.7 MJ/d、205.6 m3/d,北京分别为5.4 MJ/d、174.8 m3/d;在全天最佳百叶角度调控策略下,其南京冬至日产生的热量和干净空气量分别为热催化百叶Trombe墙系统的1.20倍和1.05倍;系统位于北京时,分别为热催化百叶Trombe墙系统的1.17倍和1.04倍。

关键词: Trombe墙; 光热复合催化; 热催化; 净化百叶; 采暖; 甲醛
中图分类号:TK519;TU18 文献标识码:A 文章编号:2095-560X（2024）01-0040-08
Performance Analysis of the Photo-Thermal Composite Catalytic Trombe Wall and the Angle Control Strategy of Blinds
FAN Miaomiao1,2, GU Tao2, LI Niansi2, YU Bendong1,2,†
1. Engineering Research Center of Building Energy Efficiency Control and Evaluation, Ministry of Education, Anhui University of Architecture, Hefei 230601, China
2. College of Urban Construction, Nanjing Tech University, Nanjing 210009, China
Abstract

Solar thermal catalytic technology can use the sun's full spectrum to generate heat collection and purify formaldehyde. Photo-thermal composite catalytic technology is a highly efficient technology that can use solar light and heat to generate heat and formaldehyde degradation simultaneously. Thermal catalysis and photo-thermal composite catalytic technology composite blinds were applied to the Trombe wall system, which used sunlight to degrade indoor gaseous pollutants while heating. This paper established the heat and mass transfer model of the Trombe wall with thermal/photo-thermal composite catalytic blinds, and experimental verification was carried out. Based on the model, the optimal control strategy of blinds for the Trombe walls was explored under the meteorological parameters of Nanjing and Beijing winter solstice (9:00-17:00). The results demonstrated excellent agreement between the established heat and mass transfer model predictions and experimental data. Notably, regions require different optimal blind angles for identical Trombe wall systems with blinds. The heat generated and clean air at the best optimal blinds for the Trombe wall with thermal catalytic blinds were 5.6 MJ/d and 196.7 m3/d, respectively. In Beijing, they were 4.6 MJ/d and 167.9 m3/d, respectively. For the Trombe wall with photo-thermal catalytic blinds system, the heat generated and clean air at the best optimal blinds were 6.7 MJ/d and 205.6 m3/d, respectively. In Beijing, they were 5.4 MJ/d and 174.8 m3/d, respectively. Under the optimal louver angle control strategy, the heat and clean air generated in the winter in Nanjing was 1.20 and 1.05 times that of the Trombe wall with photo-thermal catalytic blinds system, and 1.17 and 1.04 times that of the Trombe wall with thermal catalytic blinds system when the system was located in Beijing.

Key words: Trombe wall; photo-thermal composite catalytic; thermal-catalytic; purification blind; space heating; formaldehyde
0 引言

Trombe墙是一种具有采暖和通风功能的系统, 具有结构单一和运行维护成本较低的优点[1]。然而, 传统的Trombe墙仍然具有功能单一和太阳能利用效率较低的问题[2]。为解决上述问题, LEANG等[3]在Trombe墙中集成了相变材料, 提高了墙体的热性能。SHEN等[4]提出了一种复合Trombe墙系统, 该系统采用绝缘墙体, 增加了墙体的热阻, 减少了传统Trombe墙体系统的能量损失。为解决Trombe墙夏季过热的问题, STAZI等[5]在Trombe墙系统通风道内悬挂了百叶卷帘, 保证Trombe墙系统夏季的热舒适性。HU等[6]提出一种具有通风功能的百叶Trombe墙系统, 可以实现夏季降低室内温度和冬季采暖的功能。此外, 在气流通道中加入垂直翅片, 可以有效提高Trombe墙系统对太阳能的利用率[7]。

Trombe墙在冬季运行模式下容易出现室内空气污染物积累等问题。太阳能热催化技术与光催化技术是太阳能系统中常用的净化技术。热催化氧化（thermal catalytic oxidation, TCO）技术利用太阳全光谱发生热催化氧化反应, 具有去除污染物效率高、无二次污染等优点[8]。将热催化氧化技术集成到Trombe墙系统中, 提出热催化型Trombe墙系统, 该系统具有净化、采暖和保温的功能[9]。光催化氧化（photocatalytic oxidation, PCO）技术利用太阳光谱中的紫外部分, 反应可在常温常压下进行[10]。将光催化氧化技术和传统Trombe墙系统结合, 提出光催化型Trombe墙系统[10], 具有杀菌、降解甲醛和采暖的功能。此外, 还可将光/热催化技术与太阳能光伏光热综合利用技术结合在Trombe墙系统上, 提出光/热催化型光伏光热复合墙系统, 能够实现发电、采暖和净化的功能[11, 12]。

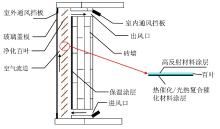
如图1所示, 在夏季, 将百叶具有高反射材料的一面朝向室外, 反射大部分太阳辐射能量; 当空气流道温度达到百叶催化涂层的启动温度时, 百叶另一面将会发生催化净化反应, 因此, 系统具有遮阳和净化的功能。在冬季, 将具有催化涂层的百叶朝向室外, 涂层吸收太阳辐射能量, 同时加热流道中的空气, 从而实现净化和采暖的功能。然而, 单一的催化净化效率不高, 太阳能光热复合催化技术不仅可以同时利用太阳光和热驱动光催化反应和热催化反应, 而且发生了光热协同效应, 提高了降解污染物的效率[13]。因此, 将光热复合催化剂喷涂在百叶型Trombe墙系统的百叶上, 提出了光热复合催化百叶Trombe墙系统, 通过调整百叶角度能够提高墙体对太阳能的利用率。

图1 热/光热复合催化百叶Trombe墙系统Fig. 1 Trombe wall with thermal/photo-thermal composite catalytic blinds

本文首先建立热催化/光热复合催化百叶Trombe墙的传热传质模型, 并进行实验验证, 然后基于模型探究热催化百叶Trombe墙和光热复合催化百叶型Trombe墙在南京和北京冬至日（9:00— 17:00）气象参数下百叶全天最佳调控策略, 并分析两种百叶型Trombe墙在最佳百叶调控策略下的最佳热性能和净化性能。

1 系统模型

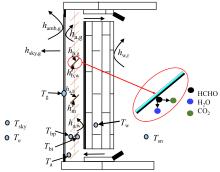
图2为百叶Trombe墙系统的传热传质模型。传热模型包括玻璃盖板、净化百叶、空气流道和蓄热墙体四个部分。

图2 百叶Trombe墙系统传热传质模型Fig. 2 Heat and mass transfer model of the blinds Trombe wall system

图2中, 传质模型为空气流道和净化百叶表面的甲醛的质量传递模型。提出如下假设：①将空气流道中的空气流动过程和甲醛降解过程视为一维过程; ②由于甲醛浓度低, 忽略气态甲醛的光热复合催化氧化的催化反应热; ③所有热物理参数均假定为常数[14]。

对于玻璃盖板, 热平衡方程式如下：

$\begin{align} & mc\frac{\text{d}{{T}_{\text{g}}}}{\operatorname{d}t}=A{{h}_{\text{e, g}}}\left( {{T}_{\text{e}}}-{{T}_{\text{g}}} \right)+A{{h}_{\text{sky, g}}}\left( {{T}_{\text{sky}}}-{{T}_{\text{g}}} \right)+ \\ & A{{h}_{\text{g, a}}}\left( {{T}_{\text{a}}}-{{T}_{\text{g}}} \right)+A{{h}_{\text{g, b}}}\left( {{T}_{\text{b}}}-{{T}_{\text{g}}} \right)+{{\alpha }_{\text{g}}}AG \\ \end{align}$ (1)

${{T}_{\text{sky}}}=0.0552{{T}_{\text{e}}}^{1.5}$ (2)

${{h}_{\text{g, b}}}=\frac{4\sigma {{\left( \frac{{{T}_{\text{g}}}+{{T}_{\text{b}}}}{2} \right)}^{3}}}{\left( {1}/{F}\; \right)+\left( 1-{{\varepsilon }_{\text{g}}} \right)/{{\varepsilon }_{\text{g}}}+\left( 1-{{\varepsilon }_{\text{b}}} \right)/{{\varepsilon }_{\text{b}}}}$ (3)

玻璃窗和百叶之间的角系数, 可通过以下公式计算[15]：

$F=1-\sin \left( \frac{{{90}^{\circ }}-\theta }{2} \right)$ (4)

玻璃与空气流道内气流之间的自然对流传热系数和辐射传热系数参考文献[16], 其经验公式如下：

$\left\{ \begin{align} & Nu=0.68+\frac{0.670R{{a}^{1/4}}}{{{\left[ 1+{{\left( 0.492/Pr \right)}^{^{9/16}}} \right]}^{4/9}}}\text{ }Ra< \text{1}{{0}^{\text{9}}} \\ & Nu={{\left\{ 0.825+\frac{0.387R{{a}^{1/4}}}{{{\left[ 1+{{\left( 0.492/Pr \right)}^{^{9/16}}} \right]}^{8/27}}} \right\}}^{2}}\text{ } Ra> \text{1}{{0}^{\text{9}}} \\ \end{align} \right.$(5)

对于空气流体, 考虑了传热和传质过程。这里假设对流热和质量均匀分布在空气流道中。热量和质量平衡方程式如下：

$mc\frac{\partial {{T}_{a}}}{\partial t}=A{{h}_{\text{b, a}}}\left( {{T}_{\text{b}}}-{{T}_{\text{a}}} \right)+A{{h}_{\text{g, a}}}\left( {{T}_{\text{g}}}-{{T}_{\text{a}}} \right)-mcu\frac{\partial {{T}_{\text{a}}}}{\partial y}$ (6)

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial y}+{{h}_{\text{m}}}\left( {{C}_{\text{s}}}-C \right)=0$ (7)

空气流速的计算基于压力平衡, 其表达式如下：

$u=\sqrt{\frac{g\beta \left( {{T}_{\text{a }\!\!\_\!\!\text{ out}}}-{{T}_{\text{a }\!\!\_\!\!\text{ in}}} \right)H}{{{f}_{\text{in}}}{{\left( A/{{A}_{\text{in}}} \right)}^{2}}+{{f}_{\text{out}}}{{\left( A/{{A}_{\text{out}}} \right)}^{2}}+f\left( H/d \right)}}$ (8)

从主流空气到催化剂传质与催化剂界面处的热催化和光热复合催化反应之间的传质平衡[17], 表达式如下：

${{r}_{\text{HCHO}}}\text{=}{{K}_{\text{app}}}{{C}_{\text{s}}}={{h}_{\text{m}}}\left( C-{{C}_{\text{s}}} \right)$ (9)

催化反应速率可根据双分子朗缪尔-欣谢尔伍德（Langmuir-Hinshelwood, L-H）动力学模型计算, 本课题组之前的研究已经验证了该动力学, 公式如下[18]：

${{r}_{\text{HCHO}}}=\frac{{{k}_{\text{HCHO}}}{{K}_{\text{HCHO}}}{{C}_{\text{HCHO}}}}{{{\left( 1+{{K}_{\text{HCHO}}}{{C}_{\text{HCHO}}} \right)}^{2}}}$ (10)

$Sh=NuL{{e}^{1/3}}$ (11)

对于净化百叶, 由于厚度非常薄, 假设每个百叶的温度是均匀的。因此, 传热方程表示如下：

$\begin{align} & mc\frac{\text{d}{{T}_{\text{b}}}}{\text{d}t}=A{{h}_{\text{b, a}}}\left( {{T}_{\text{a}}}-{{T}_{\text{tb}}} \right)+A{{h}_{\text{g, b}}}\left( {{T}_{\text{g}}}-{{T}_{\text{b}}} \right)\text{+} \\ & \text{ }A{{h}_{\text{w, b}}}\left( {{T}_{\text{w}}}-{{T}_{\text{b}}} \right)\text{+}{{\tau }_{\text{g}}}{{\alpha }_{\text{b}}}{{X}_{1}}GA \\ \end{align}$ (12)

$\left\{\begin{array}{l} \left\{\begin{array}{l} X_{1}=1 \\ X_{2}=1-\left[\sin \theta+\cos \theta \tan \left(h^{\prime}\right)\right] \end{array} \begin{array}{l} X_{1} \geq 1 \text { 时 } \end{array}\right. \\ \left\{\begin{array}{l} X_{1}=\frac{1}{\sin \theta+\cos \theta \tan \left(h^{\prime}\right)} \quad X_{1}＜1 \text { 时 } \\ X_{2}=0 \end{array}\right. \end{array}\right.$(13)

${h}'=\arctan \left[ \frac{\sin \left( {{h}_{\text{s}}} \right)}{\cos \left( {{a}_{\text{s}}}-{{a}_{\text{w}}} \right)\cos \left( {{h}_{\text{s}}} \right)} \right]$ (14)

对于墙体, 能量方程表示如下：

$\rho c\frac{\partial {{T}_{\text{w}}}}{\partial t}=\lambda \frac{{{\partial }^{2}}{{T}_{\text{w}}}}{\partial {{x}^{2}}}$ (15)

墙体外表面和内表面的边界条件如下：

$\left\{ \begin{align} & x=0:-\lambda \left( \frac{\partial {{T}_{\text{w}}}}{\partial x} \right)={{h}_{\text{a, w}}}\left( {{T}_{\text{w}}}-{{T}_{\text{a}}} \right)+{{h}_{\text{w, b}}}\left( {{T}_{\text{w}}}-{{T}_{\text{b}}} \right)+{{\tau }_{\text{g}}}{{\alpha }_{\text{w}}}G{{F}_{2}}\cdot A \\ & x={{\delta }_{\text{w}}}:-\lambda \left( \frac{\partial {{T}_{\text{w}}}}{\partial x} \right)={{h}_{\text{w, r}}}\left( {{T}_{\text{w}}}-{{T}_{\text{room}}} \right) \\ \end{align} \right.$(16)

空气采暖热效率为：

${{\eta }_{\text{th}}}=\frac{{{m}_{\text{a}}}{{c}_{\text{a}}}\left( {{T}_{\text{out}}}-{{T}_{\text{in}}} \right)}{S{{G}_{\text{solar}}}}$ (17)

甲醛的单次通过率$\varepsilon $计算公式如下：

$\varepsilon =\frac{{{C}_{\text{in}}}-{{C}_{\text{out}}}}{{{C}_{\text{out}}}}\times 100%$ (18)

洁净空气输出率（clean air delivery rate, CADR）计算公式如下：

${{R}_{\text{CAD}}}=Q\varepsilon $ (19)

2 百叶Trombe系统性能分析
2.1 实验和模型验证

采用沉淀法制备了热催化剂MnOx-CeO2, 光催化剂是粒径为4 nm的TiO2[19]。将光催化剂和热催化剂按照摩尔比为1∶ 9的比例机械搅拌混合, 制成光热复合催化剂。采用喷涂的方法将热催化剂和光热复合催化剂涂在百叶板上, 常温干燥12 h。如图3所示, 在南京工业大学江浦校区搭建了热催化百叶Trombe墙系统和光热复合催化百叶Trombe墙系统的实验台, 分别进行了相关性能探究实验。

图3 热/光热复合催化百叶Trombe墙系统实验测试装置Fig. 3 Experimental test setup of the blinds Trombe wall system

采用模拟光源为系统提供太阳辐射, 光源辐射强度和入口处气体不变。如图3, 在系统入口处通入含有一定甲醛浓度的气体, 在模拟的太阳光源照射下, 热催化百叶Trombe墙系统表面发生热催化反应, 净化空气。在系统出口处得到被系统净化后的干净空气, 测量出口处甲醛浓度。

此外, 用实际太阳光替代模拟太阳光, 进行了实验。该通风墙面朝南, 测试时间为上午9时到下午5时, 选择了2022年11月的三天, 气象数据相似, 平均太阳辐射强度分别为396、386、362 W/m2, 平均环境温度均接近18.6β ℃。分别于11月20日、24日和25日, 在15° 、45° 和75° 三个不同角度下的光热复合催化百叶Trombe墙系统进行实验, 来探究系统的热效率和甲醛降解性能。

基于南京工业大学搭建的光热复合催化百叶Trombe墙系统的实验, 将实验与模拟的数据进行了对比和计算, 如图4, 模型计算的结果与实验数据较为吻合。热催化百叶Trombe墙系统出口空气温度和热效率的均方根差（root-mean-square deviation, RMSD）分别为0.1%和1.5%; 甲醛的单次通过率和CADR的RMSD分别为0.8%和0.1%。光热复合催化百叶Trombe墙系统的出口空气温度和空气热效率的RSMD值分别为9.1%和85%; 甲醛单次转化率和CADR的RSMD值分别为8.9%和8.6%[20]。

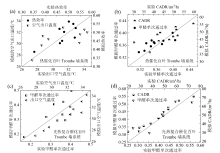图4 热催化百叶Trombe墙系统出口空气温度和热效率之间的关系（a）、甲醛单次通过率和CADR之间的关系（b）; 光热复合催化百叶Trombe墙系统出口空气温度和甲醛单次通过率之间的关系（c）、甲醛单次通过率和CADR之间的关系（d）[20]Fig. 4 The relationship between outlet air temperature and thermal efficiency (a), and the relationship between formaldehyde single-through conversion and CADR (b) of Trombe wall with thermal catalytic blinds; the relationship between outlet air temperature and formaldehyde single-through conversion (c), and the relationship between formaldehyde single-through conversion and CADR (d) of Trombe wall with photo-thermal composite catalytic blinds[20]

2.2 不同百叶角度下的性能

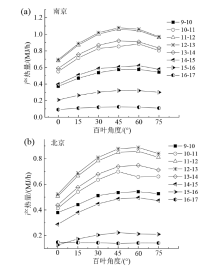
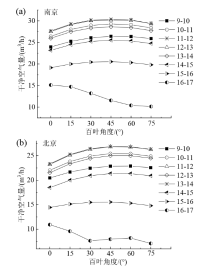
为了探究净化百叶系统的性能, 选择了南北两个典型的城市（南京和北京）典型日的气象参数进行了模拟。如图5所示, 时刻为9时至17时, 以1 h为一个时间段, 探究百叶角度分别为0° 、15° 、30° 、45° 、60° 、75° 时热催化百叶Trombe墙系统在南京冬至日（典型日）每小时的产热量。当百叶角度为0° 时, 此时百叶与水平面平行。

图5 不同百叶转角下, 热催化百叶Trombe墙系统在南京（a）和北京（b）冬至日每小时的产热量Fig. 5 Heat production per hour of Trombe wall with thermal catalytic blinds system on the winter solstice in Nanjing (a) and Beijing (b) under different blind corners

从曲线图可以看出, 随着百叶角度增加, 系统每小时的产热量呈抛物线趋势变化。由于经纬度不同, 太阳高度角不同, 百叶吸收的太阳辐射不同, 从而导致不同城市不同时刻的最佳百叶角度不同。在时间段为9-10、10-11、11-12、12-13、13-14、14-15、15-16、16-17时, 南京系统的最佳百叶角度分别为60° 、60° 、45° 、45° 、45° 、60° 、45° 、30° ; 产热量分别为0.58、0.88、1.06、1.08、0.92、0.62、0.32、0.88 MJ/h。当系统位于北京时, 在模拟的时间段内, 每小时系统的最佳百叶角度分别为60° 、45° 、60° 、60° 、60° 、60° 、45° 、0° ; 产热量分别为0.54、0.69、0.86、0.89、0.75、0.49、0.22、0.15 MJ/h。

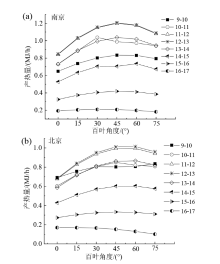
图6为南京在不同百叶翻转角度下冬至（典型日）光热复合催化百叶Trombe墙系统每小时的产热量。图中可见, 随着百叶角度的增加, 百叶Trombe墙系统每小时的产热量先逐渐增加, 而后逐渐减少。在时刻为9-17时, 每小时内系统的最佳百叶角度分别为45° 、30° 、45° 、45° 、45° 、60° 、45° 、30° ; 产热量分别为0.83、1.03、1.20、1.21、1.04、0.74、0.42、0.21 MJ/h。系统位于北京时, 在模拟的时间段内, 每小时内系统的最佳百叶角度分别为75° 、45° 、60° 、60° 、60° 、60° 、45° 、0° , 每小时产热量分别为0.25、0.32、0.39、0.40、0.34、0.22、0.10、0.06 MJ/h。

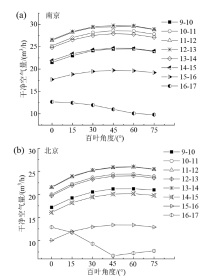
图6 不同百叶转角下, 光热复合催化百叶Trombe墙系统在南京（a）和北京（b）冬至日每小时的产热量Fig. 6 Heat production per hour of Trombe wall with photo-thermal composite catalytic blinds system on the winter solstice in Nanjing (a) and Beijing (b) under different blind corners

如图7所示, 当热催化百叶Trombe墙系统位于南京, 时刻为9-16时, 随着百叶角度的增加, 百叶Trombe墙系统每小时产生的干净空气量先逐渐增大, 而后逐渐减少。16-17时, 系统产生的干净空气量逐渐减少。在时刻为9-17时, 每小时的最佳百叶角度为60° 、45° 、45° 、45° 、45° 、45° 、45° 、0° , 每小时产生的干净空气量分别为24.5、28.6、29.5、29.7、27.9、24.7、19.7、12.7 m3/h。当系统位于北京时, 16-17时系统产生的干净空气量先减少后增加。在时刻为9-17时, 最佳百叶角度分别为60° 、60° 、60° 、60° 、60° 、60° 、45° 、0° , 每小时产生的干净空气量分别为21.2、24.4、25.8、25.9、25.0、20.1、13.4、12.9 m3/h。

图7 不同百叶转角下, 热催化百叶Trombe墙系统在南京（a）和北京（b）冬至日每小时的产生的干净空气量Fig. 7 The amount of clean air produced by Trombe wall with thermal catalytic blinds system on the winter solstice in Nanjing (a) and Beijing (b) under different blind corners

如图8所示, 当光热复合催化百叶Trombe墙系统位于南京, 在时刻为9-16时, 百叶Trombe墙系统产生的干净空气量呈抛物线趋势变化; 在16-17时, 系统产生的干净空气量逐渐减少。在9-17时, 最佳百叶角度分别为45° 、45° 、45° 、45° 、45° 、45° 、45° 、0° , 每小时产生的干净空气量分别为26.4、29.3、30.2、30.4、28.6、24.5、20.5、15.1 m3/h。当系统位于北京, 时刻为16-17时, 系统产生的干净空气量先变小后变大。时刻为9-17时每小时的最佳百叶角度为60° 、60° 、60° 、60° 、60° 、60° 、45° 、0° , 每小时产生的干净空气量分别为22.9、25.4、26.8、26.9、25.0、21.4、15.5、10.9 m3/h。

图8 不同百叶转角下, 光热复合催化百叶Trombe墙系统在南京（a）和北京（b）冬至日每小时的产生的干净空气量Fig. 8 The amount of clean air produced by Trombe wall with photo-thermal composite catalytic blinds system on the winter solstice in Nanjing (a) and Beijing (b) under different blind corners

2.3 百叶翻转角度的最佳调控策略

根据上述研究, 百叶翻转角度对百叶Trombe墙系统的节能性能和净化性能起着重要作用。如表1所示, 为了获得系统的最佳综合性能, 探讨了两种百叶Trombe墙系统在南京和北京的百叶翻转角的最佳运行策略。

表1 百叶Trombe墙系统在南京和北京的百叶翻转转角的最佳百叶调控策略 Table 1 Best louver control strategy for louver flipping corner of blind Trombe wall system in Nanjing and Beijing

以南京为例, 系统产生最大干净空气量和最多热量的百叶角度不同, 不能仅考虑热催化百叶Trombe墙系统的产热量, 其净化性能也同样重要。热催化百叶Trombe墙系统在16-17时刻, 百叶角度为60° 时, 产热量最大为0.13 MJ/h, 此时干净空气量为10.1 m3/h; 百叶角度为0° 时, 产生的干净空气量最大, 为12.7 m3/h, 此时产热量为0.92 MJ/h; 百叶角度为30° 时, 产热量为0.12 MJ/h, 此时干净空气量为12.0 m3/h; 在这种情况下, 综合考虑其性能, 选择30° 作为南京冬至日16-17时刻的百叶最佳角度。因此, 考虑两种系统的综合性能, 在时刻为9-17时百叶的最佳调控策略如表1所示。

根据表1中百叶最佳调控策略, 计算了两种百叶Trombe墙系统位于南京和北京时, 一天内产热量和干净空气量。当热催化百叶Trombe墙系统位于南京时, 基于百叶最佳调控策略, 冬至日产热量为5.6 MJ/d, 干净空气量为196.7 m3/d; 系统位于北京时, 基于百叶最佳调控策略, 冬至日产热量为4.6 MJ/d, 干净空气量为167.9 m3/d。对于光热复合催化百叶Trombe墙系统而言, 系统位于南京时, 基于百叶最佳调控策略, 冬至日产热量为6.7 MJ/d, 干净空气量为205.6 m3/d, 分别是热催化百叶Trombe墙系统的1.20倍和1.05倍; 系统位于北京时, 基于百叶最佳调控策略, 冬至日产热量为5.4 MJ/d, 干净空气量为174.8 m3/d, 分别是热催化百叶Trombe墙系统的1.17倍和1.04倍。

3 结论

（1）随着百叶角度的改变, 百叶Trombe墙系统产热量和干净空气量不同。同一百叶Trombe墙系统, 不同地区的最佳百叶角度不同。

（2）对于热催化百叶Trombe墙系统, 在冬至日9-17时刻, 南京的最佳百叶角度分别为60° 、60° 、45° 、45° 、45° 、60° 、45° 、30° , 在最佳调控策略下产热量和干净空气量分别为5.6 MJ/d、196.7 m3/d; 北京为60° 、45° 、60° 、60° 、60° 、60° 、45° 、0° , 在最佳调控策略下产热量和干净空气量分别为4.6 MJ/d、167.9 m3/d。

（3）对于光热复合催化百叶Trombe墙系统, 在冬至日9-17时刻, 南京的最佳百叶角度分别为45° 、30° 、45° 、45° 、45° 、60° 、45° 、15° , 最佳调控策略下产热量和干净空气量分别为6.7 MJ/d、205.6 m3/d; 北京为75° 、45° 、60° 、60° 、60° 、60° 、45° 、0° , 最佳调控策略下产热量和干净空气量分别为5.4 MJ/d、174.8 m3/d。

（4）光热复合催化百叶Trombe墙系统在一天中的最佳百叶角度调控策略下, 其南京冬至日产热量和干净空气量分别为热催化型Trombe墙系统的1.20倍和1.05倍; 北京冬至日产热量和干净空气量分别为热催化型Trombe墙系统的1.17倍和1.04倍。

符号表：

A 面积, m2

C 空气流道甲醛浓度, µ g/m3

c 比热容, J/(kg∙ K)

F 玻璃窗和百叶之间的视角系数

f 摩擦损失系数

G太阳辐射强度, W/m2

H 高度, m

h 换热系数, W/(m2∙ K)

m 质量, kg

r 反应速率, mg/s

S 太阳能接收面积, m2

T 温度, ℃

U 空气流速, m/s

Q空气体积流量, m3/h

X2 太阳能接收面积与总面积之比

α 吸收率

ε 单次通过率

θ 百叶翻转角度, °

δ 厚度, m

τ 透射率

β 空气的热膨胀系数, K-1

d 空气流道的水力学直径, m

Nu 努塞尔数

Ra 瑞利数

Pr 普朗特数

Le 路易斯数

Kapp表观反应系数

k 反应平衡常数

K 吸附平衡常数

X1 百叶表面无阴影的面积与热催化层的总面积的比值

下角标：

g 玻璃盖板

a 空气

e 环境

b 百叶

bp 百叶上表面

bt 百叶下表面

sky 天空

s 表面

m 催化剂内部扩散

sn 室内

w 墙体

in 入口

out 出口

HCHO 甲醛

参考文献
[1] SAADATIAN O, SOPIAN K, LIM C H, et al. Trombe walls: a review of opportunities and challenges in research and development[J]. Renewable and sustainable energy reviews, 2012, 16(8): 6340-6351. DOI: 10.1016/j.rser.2012.06.032. [本文引用:1]
[2] OMRANY H, GHAFFARIANHOSEINI A, GHAFFARIANHOSEINI A, et al. Application of passive wall systems for improving the energy efficiency in buildings: a comprehensive review[J]. Renewable and sustainable energy reviews, 2016, 62: 1252-1269. DOI: 10.1016/j.rser.2016.04.010. [本文引用:1]
[3] LEANG E, TITTELEIN P, ZALEWSKI L, et al. Numerical study of a composite Trombe solar wall integrating microencapsulated PCM[J]. Energy procedia, 2017, 122: 1009-1014. DOI: 10.1016/j.egypro.2017.07.467. [本文引用:1]
[4] SHEN J B, LASSUE S, ZALEWSKI L, et al. Numerical study on thermal behavior of classical or composite Trombe solar walls[J]. Energy and buildings, 2007, 39(8): 962-974. DOI: 10.1016/j.enbuild.2006.11.003. [本文引用:1]
[5] STAZI F, MASTRUCCI A, DI PERNA C. Trombe wall management in summer conditions: an experimental study[J]. Solar energy, 2012, 86(9): 2839-2851. DOI: 10.1016/j.solener.2012.06.025. [本文引用:1]
[6] HU Z T, HE W, HONG X Q, et al. Numerical analysis on the cooling performance of a ventilated Trombe wall combined with venetian blinds in an office building[J]. Energy and buildings, 2016, 126: 14-27. DOI: 10.1016/j.enbuild.2016.05.016. [本文引用:1]
[7] WU S Y, YAN R R, XIAO L. A novel passive solar vertical-finned-thermocatalytic-Trombe wall system for air purification and heating[J]. Journal of cleaner production, 2022, 374: 134065. DOI: 10.1016/j.jclepro.2022.134065. [本文引用:1]
[8] BAI B Y, QIAO Q, LI J H, et al. Progress in research on catalysts for catalytic oxidation of formaldehyde[J]. Chinese journal of catalysis, 2016, 37(1): 102-122. DOI: 10.1016/S1872-2067(15)61007-5. [本文引用:1]
[9] YU B D, HE W, LI N S, et al. Experimental and numerical performance analysis of a TC-Trombe wall[J]. Applied energy, 2017, 206: 70-82. DOI: 10.1016/j.apenergy.2017.08.171. [本文引用:1]
[10] YU B D, HOU J X, HE W, et al. Study on a high-performance photocatalytic-Trombe wall system for space heating and air purification[J]. Applied energy, 2018, 226: 365-380. DOI: 10.1016/j.apenergy.2018.05.111. [本文引用:2]
[11] YU B D, LIU X Y, LI N S, et al. The performance analysis of a purified PV/T-Trombe wall based on thermal catalytic oxidation process in winter[J]. Energy conversion and management, 2020, 203: 112262. DOI: 10.1016/j.enconman.2019.112262. [本文引用:1]
[12] YU B D, ZHONG D, LIU J X, et al. A novel solar PV/T driven air purification system based on heterogeneous photocatalytic reaction principles: a short review and preliminary investigation[J]. Energy conversion and management, 2020, 210: 112697. DOI: 10.1016/j.enconman.2020.112697. [本文引用:1]
[13] WEI L F, YU C L, YANG K, et al. Recent advances in VOCs and CO removal via photothermal synergistic catalysis[J]. Chinese journal of catalysis, 2021, 42(7): 1078-1095. DOI: 10.1016/S1872-2067(20)63721-4. [本文引用:1]
[14] YU B D, LI N S, JI J. Performance analysis of a purified Trombe wall with ventilation blinds based on photo-thermal driven purification[J]. Applied energy, 2019, 255: 113846. DOI: 10.1016/j.apenergy.2019.113846. [本文引用:1]
[15] HE W, HU Z T, LUO B Q, et al. The thermal behavior of Trombe wall system with venetian blind: an experimental and numerical study[J]. Energy and buildings, 2015, 104: 395-404. DOI: 10.1016/j.enbuild.2015.06.078. [本文引用:1]
[16] ZHOU F, JI J, CAI J Y, YU B D. Experimental and numerical study of the freezing process of flat-plate solar collector[J]. Applied thermal engineering, 2017, 118: 773-784. DOI: 10.1016/j.applthermaleng.2017.02.111. [本文引用:1]
[17] VERBRUGGEN S W, LENAERTS S, DENYS S. Analytic versus CFD approach for kinetic modeling of gas phase photocatalysis[J]. Chemical engineering journal, 2015, 262: 1-8. DOI: 10.1016/j.cej.2014.09.041. [本文引用:1]
[18] LI N S, GU T, XIE H, et al. The kinetic and preliminary performance study on a novel solar photo-thermal catalytic hybrid Trombe-wall[J]. Energy, 2023, 269: 126839. DOI: 10.1016/j.energy.2023.126839. [本文引用:1]
[19] 余本东. 新型太阳能光热催化型Trombe墙系统的实验和数值研究[D]. 合肥: 中国科学技术大学, 2018. [本文引用:1]
[20] LI N S, GU T, LI Y L, et al. The performance investigation on a multifunctional wall with photo-thermal catalytic blinds for heating, shading and formaldehyde removal[J]. Energy, 2023, 279: 127996. DOI: 10.1016/j.energy.2023.127996. [本文引用:1]