作者简介:虞启辉(1983-),男,博士,教授,主要从事压缩空气储能技术、新能源技术开发和利用研究。孙国鑫(1990-),男,博士,讲师,主要从事控制理论与控制工程,新能源装备与利用研究。
压缩空气储能系统可以有效减少因风能和太阳能随机性造成的弃风弃光现象,但其动态响应时间长,且存储规模配置不合理会影响其发展。为此首先提出液流电池与压缩空气储能组成混合储能系统解决并网型风光互补发电系统输出波动不稳定的问题;其次基于典型小时负荷、风力机发电功率和光伏发电功率,针对不同场景,以系统最大收益为目标函数,利用猫群算法优化压缩空气储能系统的容量配置;最后分析压缩空气储能系统的额定容量与额定功率对系统最大收益的影响,验证算法可靠性。结果表明,基于风力机与光伏系统的装机功率分别为20 MW和3.42 MW的场景,压缩空气储能系统容量配置为4 MW和46.5 MW∙h时,其经济性最佳,每周可节约购电成本183 688.24元,周最大收益为30 543.86元。
Compressed air energy storage systems can effectively reduce the phenomenon of wind and solar energy being abandoned due to their randomness. However, their dynamic response time is long, and the unreasonable configuration of storage scale will affect its development. Therefore, this paper first proposes a hybrid energy storage system composed of liquid flow battery and compressed air energy storage to solve the problem of output fluctuation instability of grid-connected wind-solar complementary power generation systems. Secondly, based on typical hour load, wind turbine generating power, and photovoltaic generating power, a system maximum profit objective function is established for different scenarios, and the capacity configuration of the compressed air energy storage system is optimized using a cat swarm algorithm. Finally, the impact of the rated capacity and rated power of the compressed air energy storage system on the system's maximum profit is analyzed to verify the reliability of the algorithm. The results show that when the installed capacity of the wind turbine and photovoltaic system is 20 MW and 3.42 MW, respectively, and the capacity configuration of the compressed air energy storage system is 4 MW and 46.5 MW∙h, respectively, achieving its best economy, and 183 688.24 yuan can be saved every week in electricity purchase costs, with a maximum weekly profit of 30 543.86 yuan.
风能、太阳能作为重要的可再生能源, 将在未来能源系统中发挥重要作用。由于风力和太阳能发电功率在时间尺度上具有互补的特性[1], 在一定程度上提高了风光联合发电系统的电能质量, 但其间歇性、波动性对电能质量的影响仍无法忽视, 而储能是提高新能源电能质量的一种有效方法[2]。
与其他储能形式相比, 压缩空气储能(compressed air energy storage, CAES)具有寿命长、环保、成本低以及储能时间长等优点[2]。但CAES响应时间长、经济效益低, 影响其商业化推广及应用。为了缩短CAES的响应时间, 提高经济效益, ZHAO等[3]设计一种由CAES和飞轮储能组成的混合储能系统, 仿真结果表明, 混合储能系统能较好地满足负荷需求, 提高风电的渗透率; JIANG等[4]提出一种由CAES和超级电容器组成的混合储能系统, 结果表明该系统既能发挥出CAES容量大的优势又能弥补CAES响应时间长的劣势。上述研究中飞轮储能和超级电容储能虽然能缓解CAES响应时间长的问题, 但两者放电时间较短(秒-分钟), 而液流电池和两者相比, 不仅响应时间和功率相同, 且放电时长为小时级[2], 更有利于储能系统稳定性。齐晓光等[5]提出一种CAES和液流电池组成的混合储能系统, 结果表明该系统不仅能缩短储能系统响应时间, 也能满足电网多性能需求。但上述模型对经济性的考虑较少。
不同的容量配置会影响储能系统的经济效益, 譬如JAVED等[6]构建了以系统总成本最小为目标函数, 以供电损失率为评价指标的风光储联合发电系统容量优化模型, 分析了评价指标对容量与成本的影响。HOU等[7]以净现值最小为目标函数, 以可再生能源利用率及负荷缺失率为评价指标进行优化, 并将混合储能容量优化结果与传统储能做对比, 验证实用性。上述文献在进行经济分析时, 只考虑容量对目标函数的影响, 未考虑储能功率对经济性的影响。
为了缩短CAES系统响应时间, 提高系统经济性, 提出一种由液流电池与CAES组成的混合储能系统。在此基础上考虑风电与光伏不确定性对CAES系统规模优化配置的影响, 并基于风电、光伏及负荷需求的典型周数据进行算例分析, 验证优化模型的可靠性。
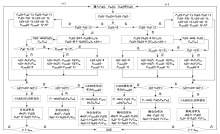
风电耦合混合储能系统由风电场、光伏电站、电网、等压绝热压缩空气储能系统(isothermal adiabatic compressed air energy storage system, IA-CAES)、液流电池、负荷需求中心等组成, 其结构示意图见图1。
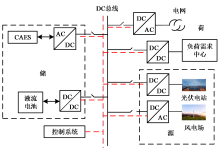 | 图1 并网型风光耦合混合储能系统结构示意图Fig. 1 Structure diagram of grid-connected wind-coupled hybrid energy storage system |
IA-CAES具有系统效率高及能量密度高等优点[7], 系统示意图如图2所示, 其主要部件由压缩机、膨胀机、换热器、储热罐、储冷罐及恒压储气室组成, 热流体与冷流体介质均为水。
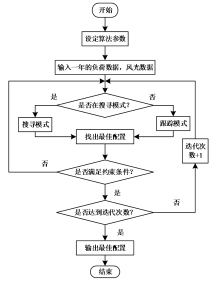
混合储能系统运行策略如图3所示, 以充电为例, 在t时刻当负荷需求功率PB小于风电场功率PWt与光伏电站功率PPv时, 系统会计算出CAES和液流电池在t0(t0 = 3 600 s)时间内充电达到容量上限所需功率分别为Pca和Pfb, Δ t1和Δ t2分别为达到CAES额定转速和额定功率所用时间, t1和t2分别为达到CAES所需转速和功率所用时间; PCAES、PCra和CCra和分别为CAES的实时功率、额定功率和额定容量; PFra和CFra和分别为液流电池的额定功率和额定容量; tmax为仿真最长时间; Δ P为CAES启动阶段1秒中功率变化值; 容量上限和下限分别为0.9和0.1。CAES充电主要有三种工况:工况1, 当压缩机未到达所需转速时, 仅液流电池工作, 工作功率为P1, 弃电功率为 |P1-PD|; 工况2, 当压缩机到达所需转速且未到达所需功率P2时, 液流电池与CAES同时工作, 液流电池与CAES工作功率分别为P1和PCAES, 弃电功率为 |P1+PCAES-PD|; 工况3, 当压缩机到P2时, 仅CAES工作, 工作功率为P2, 弃电功率为 |P2-PD|。
为了简化系统工作过程数学模型, 做如下假设:在各环节气体流通中不考虑漏气; 忽略流体在流动和换热过程中的变化及化学反应; 不考虑流体在管道中的热量损失和压力损失; IA-CAES的转速与功率为线性关系。
1.1.1 压缩阶段
储能阶段, 第i级压缩机的出口压力为:
${{p}_{\text{c}, \text{out}, i}}={{\lambda }_{i}}{{p}_{\text{c}, \text{in}, i}}$ (1)
式中:pc, in, i和λ i分别是第i级压缩机入口压力和压缩比。
第i级压缩机的等熵出口温度为:
${{T}_{\text{c}, \text{out}, i}}={{T}_{\text{c}, \text{in}, i}}+{{{T}_{\text{c}, \text{in}, i}}\left[ {{\left( {{\lambda }_{i}} \right)}^{\frac{\gamma -1}{\gamma }}}-1 \right]}/{{{\eta }_{\text{c}}}}\; $ (2)
式中:γ 为绝热指数; Tc, in, i为第i级压缩机入口温度。
非设计工况下等熵效率[8]为:
${{\eta }_{\text{c}}}=\eta _{\text{c}}^{0}\left[ 1-{{a}_{4}}{{\left( 1-{{{\bar{n}}}_{\text{c}}} \right)}^{2}} \right]\left( {{{{\bar{n}}}_{\text{c}}}}/{{{{\bar{m}}}_{\text{c}}}}\; \right)\left( 2-{{{{\bar{n}}}_{\text{c}}}}/{{{{\bar{m}}}_{\text{c}}}}\; \right)$ (3)
其中$\bar{m}_{c}$与$\bar{n}_{c}$的表达式分别为:
${{\bar{m}}_{\text{c}}}=\frac{{{{m}_{\text{c}}}\sqrt{T_{\text{c}, \text{in}, i}^{0}}}/{{{p}_{\text{c}, \text{in}, i}}}\; }{{m_{\text{c}}^{0}\sqrt{T_{\text{c}, \text{in}, i}^{0}}}/{p_{\text{c}, \text{in}, i}^{0}}\; }$ (4)
${{\bar{n}}_{\text{c}}}=\frac{{{{n}_{\text{c}}}}/{\sqrt{{{T}_{\text{c}, \text{in}, i}}}}\; }{{n_{\text{c}}^{0}}/{\sqrt{T_{\text{c}, \text{in}, i}^{0}}}\; }$ (5)
式中:nc和mc分别为压缩机实际转速与实际质量流量; 上标0代表设计工况条件。
压缩阶段压缩机组做功为:
${{W}_{\text{c}}}=\int_{0}^{{{t}_{\text{c}}}}{{{c}_{p, \text{a}}}\sum\limits_{i=1}^{3}{{{m}_{\text{c}}}\left( {{T}_{\text{c}, \text{out}, i}}-{{T}_{\text{c}, \text{in}, i}} \right)}}\text{d}t$ (6)
式中:cp, a为空气比热容; tc为充电时间。
换热器的有效性系数定义为[9]:
$\varepsilon =\frac{1-exp\left[ \left( -{{N}_{\text{TU}}} \right)\left( 1+{{C}_{\text{r}}} \right) \right]}{1-{{C}_{\text{r}}}\exp \left[ \left( -{{N}_{\text{TU}}} \right)\left( 1+{{C}_{\text{r}}} \right) \right]}$ (7)
其中Cr与NTU的表达式分别为:
${{C}_{\text{r}}}=\frac{{{\left( {{c}_{p, \text{a}}}{{m}_{\text{c}}}, {{c}_{p, \text{w}}}{{m}_{\text{w}}} \right)}_{\min }}}{{{\left( {{c}_{p, \text{a}}}{{m}_{\text{c}}}, {{c}_{p, \text{w}}}{{m}_{\text{w}}} \right)}_{\max }}}$ (8)
${{N}_{\text{TU}}}=\frac{{{U}_{\text{A}}}}{{{\left( {{c}_{p, \text{a}}}{{m}_{\text{c}}}, {{c}_{p, \text{w}}}{{m}_{\text{w}}} \right)}_{\min }}}$ (9)
式中:cp, w和mw分别为工作流体的比热容和质量流量。UA为2 500 W/K[9]。
i+1级压缩机入口温度为:
${{T}_{\text{c}, \text{in}, i+1}}=\left( 1-\varepsilon \right){{T}_{\text{c}, \text{out}, i}}+\varepsilon {{T}_{\text{cold}}}$ (10)
式中:Tcold为低温储热罐的温度。
1.1.2 等压储气阶段
压缩空气储气罐中的空气质量为:
${{M}_{\text{car}}}={{M}_{\text{car}}}\left( 0 \right)+\int_{0}^{t}{\left( {{m}_{\text{c}}}-{{m}_{\text{t}}} \right)}\ \text{d}t$ (11)
式中:Mcar(0)为初始状态下储存罐中的空气质量; mt为膨胀机中空气质量流量。
储气容量的表达式为:
${{S}_{\text{ca}}}\left( t \right)=\frac{{{M}_{\text{car}}}\left( t \right)-{{M}_{\min }}}{{{M}_{\max }}-{{M}_{\min }}}$ (12)
式中:Mmax和Mmin分别为储气罐最大和最小空气质量。
1.1.3 释能阶段
释能过程膨胀机的入口温度为:
${{T}_{\text{t}, \text{in}, j}}=\left( 1-\varepsilon \right){{T}_{\text{t}, \text{out}, j-1}}+\varepsilon {{T}_{\text{hot}}}$ (13)
式中:Tt, out, j-1为第j-1级膨胀机出口温度; Thot为高温储热罐的温度。
第j级膨胀机出口压力为:
${{p}_{\text{t}, \text{out}, j}}=\frac{{{p}_{\text{t}, \text{in}, j}}}{{{\lambda }_{j}}}$ (14)
式中:λ j为膨胀机的压缩比。
非设计工况下膨胀机的等熵效率为:
${{\eta }_{\text{t}}}=\eta _{\text{t}}^{0}\left[ 1-0.3{{\left( 1-{{{\bar{n}}}_{\text{t}}} \right)}^{2}} \right]\left( {{{{\bar{n}}}_{\text{t}}}}/{{{{\bar{m}}}_{\text{t}}}}\; \right)\left( 2-{{{{\bar{n}}}_{\text{t}}}}/{{{{\bar{m}}}_{\text{t}}}}\; \right)$ (15)
其中$\bar{m}_{t}$与$\bar{n}_{t}$的表达式分别为:
${{\bar{m}}_{\text{t}}}=\sqrt{1.4-0.4\frac{{{n}_{\text{t}}}}{n_{\text{t}}^{0}}}\sqrt{\frac{{{\left( {{{p}_{\text{t}, \text{out}, j}}}/{{{p}_{\text{t}, \text{in}, j}}}\; \right)}^{2}}-1}{{{\left( {p_{\text{t}, \text{out}, j}^{0}}/{p_{\text{t}, \text{in}, j}^{0}}\; \right)}^{2}}-1}}$ (16)
${{\bar{n}}_{\text{t}}}=\frac{{{{n}_{\text{t}}}}/{\sqrt{{{T}_{\text{t}, \text{in}, j}}}}\; }{{n_{\text{t}}^{0}}/{\sqrt{T_{\text{t}, \text{in}, j}^{0}}}\; }$ (17)
式中:nt为膨胀机转速。
第j级膨胀机出口温度为[8]:
${{T}_{\text{t}, \text{out}, j}}={{T}_{\text{t}, \text{in}, j}}-{{\eta }_{\text{t}}}{{T}_{\text{t}, \text{in}, j}}\left[ 1-{{\left( \frac{{{p}_{\text{t}, \text{out}, j}}}{{{p}_{\text{t}, \text{in}, j}}} \right)}^{\frac{\gamma -1}{\gamma }}} \right]$ (18)
膨胀阶段的输出功为:
${{W}_{\text{t}}}=\int_{0}^{{{t}_{\text{dis}}}}{{{c}_{p, \text{a}}}\sum\limits_{j=1}^{3}{{{m}_{\text{t}}}\left( {{T}_{\text{t}, \text{out}, j}}-{{T}_{\text{t}, \text{in}, j}} \right)}}\text{d}t$ (19)
式中:tdis为放电时间。
液流电池采用恒定功率来储能和释能, 其表达式为[10]:
${{S}_{\text{fb, ch}}}\left( t \right)={{S}_{\text{fb}}}\left( t-1 \right)+\left( \frac{{{\eta }_{\text{ch}}}}{{{C}_{\text{Fra}}}}\int_{0}^{{{t}_{_{\text{F1}}}}}{{{P}_{\text{Fch}}}\text{d}t} \right)$ (20)
${{S}_{\text{fb, dis}}}\left( t \right)={{S}_{\text{fb}}}\left( t-1 \right)-\left( \frac{{{\eta }_{\text{dis}}}}{{{C}_{\text{Fra}}}}\int_{0}^{{{t}_{_{\text{F2}}}}}{{{P}_{\text{Fdis}}}\text{d}t} \right)$ (21)
式中:Sfb, ch(t)和Sfb, dis(t)分别为充电和放电后t时刻的液流电池储能容量; Sfb(t-1)为t-1时刻的液流电池储能容量; PFch、PFdis、η ch、η dis分别为液流电池的充电功率、放电功率、储能效率和释能效率; tF1、tF2分别为液流电池的储能时间和释能时间。
以混合储能系统的最大收益为目标函数, 其表达式为:
$U=\max \left[ \begin{align} & {{Y}_{\text{SE}}}+{{Y}_{\text{EP}}}-{{C}_{\text{BE}}}- \\ & \left( {{C}_{\text{IN}}}+{{C}_{\text{OM}}} \right)\times 7/{{N}_{\text{days}}} \\ \end{align} \right]$ (22)
式中:YSE为售电收益; YEP为环保收益; CIN为安装成本; CBE为购电成本; COM为维护成本; Ndays为一年系统工作天数。其中式(22)中各项参数表达式为:
$\left\{\begin{aligned} Y_{\mathrm{SE}}+ & Y_{\mathrm{EP}}-C_{\mathrm{BE}}=P_{\mathrm{yh}}(t) c_{\mathrm{gs}}(t)+P_{\mathrm{L}}(t) c_{\mathrm{gb}}(t)+ \\ & {\left[P_{\mathrm{L}}(t)-P_{\mathrm{G}}(t)\right] c_{\mathrm{En}}+P_{\mathrm{G}}(t) R_{\mathrm{s}}(t) } \\ C_{\mathrm{IV}}= & \left(\begin{array}{l} N_{\mathrm{Wt}} R_{\mathrm{Wt}}+S_{\mathrm{Pv}} R_{\mathrm{Pv}}+P_{\mathrm{Cra}} c_{\mathrm{Inv}, \mathrm{p} 1}+ \\ C_{\mathrm{Cra}} c_{\mathrm{Inv}, \mathrm{cl}}+P_{\mathrm{Fra}} c_{\mathrm{Inv}, \mathrm{p} 2}+C_{\mathrm{Fra}} c_{\mathrm{Inv}, \mathrm{c} 2} \end{array}\right) \frac{r(1+r)^{L}}{(1+r)^{L}-1} \\ C_{\mathrm{OM}}= & C_{\mathrm{Cra}} O_{\mathrm{M}, \mathrm{C}}+C_{\mathrm{Fra}} O_{\mathrm{M}, \mathrm{F}}+R_{\mathrm{Wt}} O_{\mathrm{M}, \mathrm{Wt}}+R_{\mathrm{Pv}} O_{\mathrm{M}, \mathrm{Pv}} \end{aligned}\right.$(23)
式中:Pyh(t)、cgs(t)、PL(t)、cgb(t)、PG(t)分别为t时刻的售电功率、售电价格、负荷功率、上网电价及购电功率; cEn为环保收益[7]; NWt、RWt分别为风力机数量和单位价格; SPv、RPv分别为光伏面积和单位价格; cInv, c1和cInv, p1分别为IA-CAES单位功率和容量的安装成本; cInv, c2和cInv, p2分别为液流电池单位功率和容量的安装成本; r为投资利率; L为混合储能系统寿命; OM, C、OM, F、OM, Wt、OM, Pv分别为IA-CAES、液流电池储能系统、风机和光伏系统的单位容量维护成本。
系统的功率约束是优化容量配置的重要因素之一。该系统功率及容量约束为:
$\left\{ \begin{align} & {{P}_{\text{Wt}}}\left( t \right)+{{P}_{\text{Pv}}}\left( t \right)+{{P}_{\text{t}}}\left( t \right)+{{P}_{\text{Fdis}}}\left( t \right){{\eta }_{\text{F}}}+{{P}_{\text{G}}}= \\ & {{P}_{\text{B}}}\left( t \right)+{{P}_{\text{c}}}\left( t \right)+{{P}_{\text{Fch}}}\left( t \right)/{{\eta }_{\text{ch}}}+{{P}_{\text{du}}}(t)\text{ } \\ & 0\le {{P}_{\text{c}}}\left( t \right)+{{P}_{\text{t}}}\left( t \right)\le {{P}_{\text{Cr}}} \\ & 0\le {{P}_{\text{Fch}}}\left( t \right)+{{P}_{\text{Fdis}}}\left( t \right)\le {{P}_{\text{Fr}}} \\ & 0\le {{W}_{\text{Wt}}}+{{W}_{\text{Pv}}}+{{W}_{\text{ca}}}+{{W}_{\text{fb}}}\le 10P_{\text{B}}^{\max } \\ \end{align} \right.$ (24)
式中:Wwt、WPv、Wca、Wfb分别为风力机、光伏系统、IA-CAES和液流电池的额定容量。混合储能系统的容量约束为最大负荷的10倍[7]。
选取内蒙古某地区(N 39° 61′ 、E 109° 78′ )为参考, 参照文献[12]选取典型日的方法, 建立典型周数据模型, 该地区一周典型小时负荷需求曲线如图5所示。风电场与光伏电站的数学模型参考文献[6]。单台额定功率为2.5 MW的风力机与1 m2额定功率为0.4 kW的光伏系统平均每小时输出功率分别为0.89 MW、0.15 kW, 采用85% + 15%风光出力比例[13], 并综合考虑实际发电量与需求负荷的影响, 确定具有可行性的风力发电与光伏发电调度策略, 场景设置见表1。
| 表1 场景设置 Table 1 Scene setting |
表2为风电耦合混合储能系统的基本参数。IA-CAES和液流电池初始储能容量为额定储能容量的50%, 且储能容量范围限制在10% ~ 90%; IA-CAES以0.5 MW∙ h和0.5 MW的步长在约束范围内全局寻优。出售电价与上网电价执行2022年内蒙古自治区的电网电价。
不同数量的风力机和光伏系统共同作用下, 风光耦合混合储能系统的经济效益情况见表3。根据求解算法得到不同场景下IA-CAES最佳容量配置, 在此基础上, 随着风力机和光伏系统数量的增加, 系统购电量、减少弃电量及最大收益均为先增大后减少。场景1中风电场与光伏电站每小时实际输出功率仅为6.28 MW, 远小于负荷需求, 购电量为减少弃电量的2.77倍, 使得最大收益为负; 场景2中风电场与光伏电站每小时实际输出功率为7.33 MW, 小于负荷需求, 购电量成本增加, 使得最大收益较小; 场景3中风电场与光伏电站每小时实际输出功率为8.38 MW, 接近负荷需求8.82 MW, 在IA-CAES最佳配置下, 可减少弃电量147.32 MW∙ h, 购电量仅为5.71 MW, 最大收益为30 543.86元; 场景4和场景5由于风力机与光伏系统数量过多, 使系统投资及运行成本增加, 但减少的弃电量急速下降, 出现最大收益下滑的现象。综上, 针对负荷需求的变化, 确定合理的风力机与光伏系统运行数量, 并配置最佳的IA-CAES容量存储规模可有效提升系统的经济效益。对于典型小时负荷为8.82 MW的工厂用户, 采用8台风力机与8 547 m2光伏系统(风力机与光伏系统的装机功率分别为20 MW和3.42 MW)是可行的。下面将进一步分析IA-CAES的额定容量与功率对系统收益的影响。
| 表3 多场景最大收益分析 Table 3 Multi-scenario maximum benefit analysis |
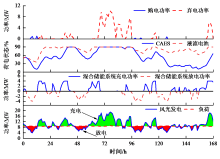
液流电池仅在IA-CAES系统充电和放电过程中发挥作用, 最大作用时间为5 min, 设计液流电池的额定功率与额定容量分别为8 MW和1.5 MW∙ h。压缩机与膨胀机额定转速皆为8 000 r/min[9], 图6是在场景3中压缩机需要以4 MW功率充电时混合储能系统功率响应曲线。在压缩机未达8 000 r/min时, 液流电池进行充电; 当压缩机达到8 000 r/min且未达到4 MW时, IA-CAES与液流电池共同充电; 当压缩机达到4 MW时, 液流电池停止充电。
在场景3中, 风光耦合混合储能系统的电力调度如图7所示, 一周中购电量仅为5.71 MW∙ h, 弃电功率为146.49 MW∙ h, 弃电区间占总时长的10.71%。图中液流电池未达到最低容量且仅有5.95%时间容量低于50%, 所选容量符合设计要求; 压缩空气储能处于容量上限和下限的时间占总时间的百分比为15.47%, 且一周循环后容量大于50%, 确保了混合储能系统周期性、可重复利用的功效, 验证了模型的可靠性。
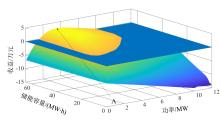
IA-CAES系统容量优化配置过程如图8所示, 其中蓝色平面表示收益为0的曲面, 随着额定容量与额定功率的增加, 系统最大收益先增大后减小, 表明在A点收益最大, 此点额定容量为46.5 MW∙ h、额定功率为4 MW时, 可获得最大收益30 543.86元。
为改善风光波动性、需求负荷不确定性及IA-CAES动态响应慢等问题, 建立了非工况IA-CAES系统模型, 以液流电池作为改善IA-CAES 动态响应慢的问题, 并采用猫群算法求解以最大收益为优化目标的最佳容量配置, 算例分析表明:
(1)风力机数量会影响风光耦合系统的经济效益, 风力机数量增多会增加系统弃电量, 并使投资成本增加; 风力机数量减少会增加大额的购电成本。综合分析结果显示选择风力机与光伏系统的装机功率分别为20 MW和3.42 MW时经济效益最佳。
(2)对于IA-CAES和液流电池配置额定功率分别为4 MW、8 MW, 额定容量分别为46.5 MW∙ h、1.5 MW∙ h时可满足用户小时负荷8.82 MW的电力需求, 每周可节约购电成本183 688.24元, 周最大收益为30 543.86元。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|