作者简介:解非(1997-),男,硕士研究生,主要从事智能微电网技术中的电力电子研究。舒 杰(1969-),男,博士,研究员,主要从事分布式可再生能源发电、智能微电网技术研究。
针对三有源桥变换器解耦控制中工况远离稳态点解耦矩阵变化时控制性能较差的问题,提出一种基于线性二次型调节器(LQR)的三有源桥变换器控制方法。通过电路等效变换和端口功率传输方程建立状态空间模型,进一步设计基于状态反馈的LQR控制方法,在实现功率潮流控制的同时保持端口电压的稳定,通过仿真控制验证所提出方法的控制性能,对比传统PI解耦控制,在工况变化时,该控制方法具有更好的动态性能。
To improve the dynamic performance in the decoupling control of triple-active bridge converter when the working condition is far from the operating point and the decoupling matrix changes, a control method of triple-active bridge based on linear quadratic regulator (LQR) is proposed. The state-space model is established by circuit equivalent transformation and power transmission equation among each port, and the LQR control method based on state feedback is further designed to control the power flow while maintaining the stability voltage of each port irrespective of the operating point. The control performance of the method proposed in this paper is verified by simulation control. Compared with traditional PI decoupling control, the proposed method has better control performance when working conditions change.
为了适应新能源发电的广泛接入和分布式储能的大力推广[1], 具有变压、电气隔离、功率传输与控制, 高功率密度和效率, 可直接接入可再生能源与储能系统等特点的电力电子变压器(power electronic transformer, PET)成为研究关注的重点[2]。多端口直流PET可以同时连接分布式电源、储能系统与直流负载, 实现功率的控制与传输, 实现可再生能源的就地消纳, 避免了在电能转换与传输环节的损耗。多端口直流PET从拓扑上可分为共直流母线型[3]和共交流母线型。共直流母线型PET由各端口连接变换器后直接接入到公共直流母线上, 可以对每个端口变换器单独进行控制以实现功率传输的控制, 且端口可以拓展, 控制较简单, 缺点是变换器的数量多, 电能需要经过多级转换, 效率和可靠性都会降低[4]。共交流母线型PET也可称为多有源桥型变换器[5], 通过共用高频多绕组变压器的磁链, 各绕组经有源桥电路整流提供直流输出, 直接连接各端口, 具有端口间相互隔离、开关器件少、电能只经过一级转换、功率密度和效率高等特点[6], 但由于共用磁链, 不同端口间的功率相互耦合, 在控制上较为复杂。
研究人员针对有源桥型变换器的控制开展了大量的研究工作。ZHAO等[7]通过小信号分析, 在控制中增加前馈解耦矩阵, 实现比例积分(proportional-integral, PI)解耦控制, 但解耦矩阵随着电路的工作情况改变而实时变化[8], 只在解耦的稳态点附近能取得较好的控制效果[9], 在解耦矩阵变化时控制效果较差。宋家康等[9]提出了一种基于神经网络的三有源桥(triple-active bridge, TAB)变换器解耦矩阵计算方法, 得到不同工况的解耦矩阵后以查表法提供控制参数, 提升了解耦控制性能, 但需要离线计算解耦矩阵的参数并额外存储, 实现较复杂。杨旭等[10]在全桥中加入LC串联谐振网络, 通过硬件解耦减小了端口功率的耦合, 但对变换器的工作范围有一定限制。现代控制理论的方法也被应用于多端口变换器控制中, 年珩等[11]通过模型预测控制提升了端口的动态响应能量但求解移相角计算复杂, 自抗扰控制(active disturbance rejection control, ADRC)[12]和滑模控制[13]在TAB控制中也实现了较好的解耦控制效果, 但均未考虑变换器启动时的过冲且控制较为复杂。
对于TAB变换器的多输入多输出耦合系统, 相比传统的PI控制, 线性二次型调节器(linear quadratic regulator, LQR)控制基于状态反馈, 通过特征值的预设[14], 能使系统获得期望的性能, 具有更快的动态响应速度, 被广泛应用于多输入多输出系统的控制设计中[15]。
基于上述研究, 针对TAB变换器解耦控制依赖于稳态点且解耦矩阵变化时控制性能较差的问题, 提出一种基于LQR的TAB变换器的端口电压控制方法, 通过建立TAB变换器的状态空间模型, 设计TAB变换器的LQR最优控制器, 实现TAB变换器的端口电压控制, 提升响应速度与控制性能, 最后通过仿真对研究内容进行验证。
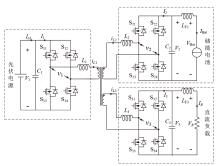
TAB变换器拓扑如图1所示, 三个直流端口分别接光伏电源、储能电池与直流负载。Vi为端口i的全桥输入直流电压; Io1为端口1的输入电流; Ii为端口i的全桥输入电流; 辅助电感Li为各个端口的功率传输电感与对应绕组的漏感之和; Ci和LFi是端口i直流侧的稳压滤波电容与电感; 各端口由共磁链的三绕组高频变压器连接, Ni为高频变压器绕组i的匝数; vi为端口i对应的全桥电路逆变输出的高频方波电压; iLi为端口i对应的辅助电感Li上的电流, 电路中的器件均为理想元件。
经电路等效变换后可得TAB变换器的等效电路如图2所示[16]。
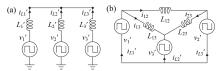 | 图2 TAB变换器等效电路:(a)星形电路; (b)三角形电路Fig. 2 Equivalent circuit of TAB converter: (a) star equivalent circuit; (b) mesh equivalent circuit |
以端口1为参考, 将第k端口的各参数折算到端口1后的全桥电路输出的高频方波电压, 电感电流和辅助电感的大小分别记为vk′ 、ik′ 和Lk′ , k= 1 ~ 3, 计算公式如下:
$\left\{ \begin{align} & {{v}_{k}}\prime =\left( \frac{{{N}_{1}}}{{{N}_{k}}} \right){{v}_{k}} \\ & {{i}_{Lk}}\prime =\left( \frac{{{N}_{k}}}{{{N}_{1}}} \right){{i}_{Lk}} \\ & {{L}_{k}}\prime ={{\left( \frac{{{N}_{1}}}{{{N}_{k}}} \right)}^{2}}{{L}_{k}} \\ \end{align} \right.$ (1)
图2(b)中各端口间等效电感Lij表达式为:
${{L}_{ij}}={{L}_{i}}\prime {{L}_{j}}\prime \left( \sum\limits_{k=1}^{n}{\frac{1}{{{L}_{k}}\prime }} \right)$ (2)
为了方便分析与计算, 令各绕组匝比都相同, 记N= N1=N2=N3, 令各端口之间电感也相同, 记L= L12= L13= L23。
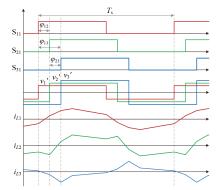
TAB 变换器通常采用移相调制, 所有开关的频率f相同, 以对称占空比导通关断, 同一全桥中相同桥臂上的开关管驱动信号互补, 对角开关管驱动信号互补, 经全桥电路逆变输出高频方波电压。以端口1开关管驱动信号为参考, 端口2、3驱动信号滞后的移相角分别记为φ 12和φ 13, 则端口2、3之间的移相角为φ 23= φ 13- φ 12, 其工作原理波形如图3所示, Ts为一个开关周期, Ts = 1/f。
此时, 结合图2(b)的等效电路, TAB变换器各端口传输的功率Pi可以等效为三组双有源桥(dual-active bridge, DAB)变换器间单移相控制下传输的功率叠加, 其表达式为:
$\left\{ \begin{align} & {{P}_{1}}=\frac{{{V}_{1}}{{V}_{2}}{{\varphi }_{12}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{12}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)+\frac{{{V}_{1}}{{V}_{3}}{{\varphi }_{13}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{13}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ & {{P}_{2}}=-\frac{{{V}_{1}}{{V}_{2}}{{\varphi }_{12}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{12}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)+\frac{{{V}_{2}}{{V}_{3}}{{\varphi }_{23}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{23}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ & {{P}_{3}}=-\frac{{{V}_{1}}{{V}_{3}}{{\varphi }_{13}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{13}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)-\frac{{{V}_{2}}{{V}_{3}}{{\varphi }_{23}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{23}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ \end{align} \right.$ (3)
从式(3)中可以看出, TAB变换器任意端口传输功率的变化不仅与当前端口的移相角和电压有关, 还受到其余各个端口的移相角和电压的影响, 当其中一个端口的传输功率或者移相角发生变化时, 会引起其余端口传输功率及端口电压与电流的波动, 即各端口的传输功率之间存在耦合关系。由上式可得到各端口的电流Ii为:
$\left\{ \begin{align} & {{I}_{1}}=\frac{{{V}_{2}}{{\varphi }_{12}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{12}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)+\frac{{{V}_{3}}{{\varphi }_{13}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{13}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ & {{I}_{2}}=-\frac{{{V}_{1}}{{\varphi }_{12}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{12}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)+\frac{{{V}_{3}}{{\varphi }_{23}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{23}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ & {{I}_{3}}=-\frac{{{V}_{1}}{{\varphi }_{13}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{13}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)-\frac{{{V}_{2}}{{\varphi }_{23}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{\left| {{\varphi }_{23}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ \end{align} \right.$ (4)
在变换器工作过程中, 一般需要保持端口电压的稳定, 即以端口电压的给定参考值作为控制目标, 端口2接储能电池作为功率平衡端口, 在光伏电源输出大于负载所需功率时吸收多余功率充电, 在光伏电源输出不足时输出功率放电保证负载正常工作, 其电流参考值IBat* 可由功率守恒得到。
当电路工作在稳态时, 将稳态点的参数记为端口2电流IBat* 、端口2电压VBat* 、端口3电流IR* 、端口3电压VR* 、端口驱动信号移相角φ k* , 以端口1作为参考, 令φ 1= 0, 同时忽略端口1的电压波动, 设小信号扰动分别为Δ Ik、Δ Vk、Δ φ k, k= 2, 3代入式(4)中, 展开后忽略高阶小项, 将式(4)中的电流变化表示为各端口直流电压变化和移相角变化的函数的线性化模型为:
$\left\{ \begin{align} & \Delta {{I}_{2}}={{G}_{22}}\Delta {{\varphi }_{2}}+{{G}_{23}}\Delta {{\varphi }_{3}}+{{H}_{22}}\Delta {{V}_{2}}+{{H}_{23}}\Delta {{V}_{3}} \\ & \Delta {{I}_{3}}={{G}_{32}}\Delta {{\varphi }_{2}}+{{G}_{33}}\Delta {{\varphi }_{3}}+{{H}_{32}}\Delta {{V}_{2}}+{{H}_{33}}\Delta {{V}_{3}} \\ \end{align} \right.$ (5)
其中系数为:
$\left\{ \begin{align} & {{G}_{ik}}=\frac{\partial {{I}_{i}}}{\partial {{\varphi }_{k\ne i}}}=\frac{{{V}_{k}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{2\left| {{\varphi }_{k}}-{{\varphi }_{i}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ & {{G}_{ii}}=\frac{\partial {{I}_{i}}}{\partial {{\varphi }_{i}}}=-\sum\limits_{j\ne i}^{n}{\frac{{{V}_{j}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( 1-\frac{2\left| {{\varphi }_{j}}-{{\varphi }_{i}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right)} \\ & {{H}_{ij}}=\frac{\partial {{I}_{i}}}{\partial {{V}_{j}}}=\frac{{{V}_{j}}}{2\text{ }\!\!\pi\!\!\text{ }fL}\left( {{\varphi }_{j}}-{{\varphi }_{i}} \right)\left( 1-\frac{\left| {{\varphi }_{j}}-{{\varphi }_{i}} \right|}{\text{ }\!\!\pi\!\!\text{ }} \right) \\ \end{align} \right.$ (6)
将端口驱动信号移相角变化定义为控制变量:
$\begin{matrix} {{u}_{1}}=\Delta {{\varphi }_{2}}={{\varphi }_{2}}-\varphi _{2}^{* } & {{u}_{2}}=\Delta {{\varphi }_{3}}={{\varphi }_{3}}-\varphi _{3}^{* } \\ \end{matrix}$ (7)
将端口电压与电流定义为状态量与输出量:
$\begin{matrix} {{x}_{1}}={{y}_{1}}={{V}_{2}}-V_{\text{Bat}}^{* } & {{x}_{2}}={{y}_{2}}={{V}_{3}}-V_{R}^{* } \\ {{x}_{3}}={{y}_{3}}={{I}_{\text{Bat}}}-I_{\text{Bat}}^{* } & {{x}_{4}}={{y}_{4}}={{I}_{R}}-I_{R}^{* } \\ \end{matrix}$ (8)
将其写为状态空间方程的形式:
$\dot{x}=Ax\text{+}Bu$ (9)
结合图1中电路关系与上式可以推出系统矩阵A和控制矩阵B分别为:
$\begin{matrix} \mathsf{A}=\left[ \begin{matrix} \frac{{{H}_{22}}}{{{C}_{2}}} & \frac{{{H}_{23}}}{{{C}_{2}}} & \frac{-1}{{{C}_{2}}} & 0 \\ \frac{{{H}_{32}}}{{{C}_{3}}} & \frac{{{H}_{33}}}{{{C}_{3}}} & 0 & \frac{-1}{{{C}_{3}}} \\ \frac{1}{{{L}_{\text{F2}}}} & 0 & 0 & 0 \\ 0 & \frac{1}{{{L}_{\text{F3}}}} & 0 & 0 \\ \end{matrix} \right] & \mathsf{B}=\left[ \begin{matrix} \frac{{{G}_{22}}}{{{C}_{2}}} & \frac{{{G}_{23}}}{{{C}_{2}}} \\ \frac{{{G}_{32}}}{{{C}_{3}}} & \frac{{{G}_{33}}}{{{C}_{3}}} \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right] \\ \end{matrix}$ (10)
输出矩阵C与直接转移矩阵D为:
$\begin{matrix} \mathsf{C}={{\mathsf{I}}_{4\times 4}} & \mathsf{D}={{0}_{4\times 4}} \\ \end{matrix}$ (11)
通过引入代价函数J的概念对系统的控制性能进行评价:
$J=\frac{1}{2}\int_{{{t}_{\text{0}}}}^{\infty }{\left( {{x}^{\text{T}}}Qx+{{u}^{\text{T}}}Ru \right)\text{d}t}$ (12)
LQR控制的本质是通过设计出的状态反馈控制器K使代价函数J取得最小值, 即找到一组控制量u使得同时有x足够小(系统达到稳定状态)且u足够小(控制量尽量小的变化), 即通过最小的控制代价使系统达到最终的控制目标, 得到最佳的控制效果。式(12)中Q与R分别为代价函数中状态量和控制量的权重矩阵, 决定着控制的收敛速度和能耗, K由矩阵Q与R唯一决定, 构造满足下式的矩阵P:
$\frac{\text{d}}{\text{d}t}\left( {{x}^{\text{T}}}Px \right)=-{{x}^{\text{T}}}\left( Q\text{+}{{K}^{\text{T}}}RK \right)x$ (13)
将式(13)代入式(12)中, 当代价函数J取得最小值时, 矩阵P为Riccati方程式(14)的解:
${{A}^{\text{T}}}P\text{+}PA\text{+}Q-PB{{R}^{-\text{1}}}{{B}^{\text{T}}}P=0$ (14)
可以进一步得到系统的状态反馈控制量为:
$u=-{{R}^{-\text{1}}}{{B}^{\text{T}}}Px=-Kx$ (15)
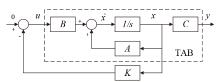
TAB变换器的LQR控制框图如图4所示。
代价函数J对系统的状态量和控制量进行了综合评价, 通过对Q与R中元素的调整可以改变系统的特征值位置, 从而改变系统的控制性能。在LQR控制下, 每个控制动作给出的控制量即端口驱动信号移相角φ 2与φ 3的偏差都尽可能小, 最小化控制过程中带来的影响, 以实现系统控制的最优解。
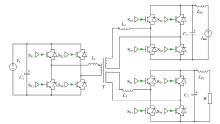
利用Simulink/PLECS联合仿真, 搭建基于LQR控制的TAB变换器模型如图5所示, 具体仿真参数如表1所示。
| 表1 仿真参数 Table 1 Simulation parameters |
为验证本文提出的TAB变换器LQR控制方法的控制效果, 选择前馈解耦的PI控制方法[7]作为对比, 两种控制方法的仿真中电路元件基本参数设置完全相同。PI解耦控制的PI控制器参数与LQR的反馈矩阵K参数设计如表2所示。
| 表2 控制器参数 Table 2 Controller parameters |
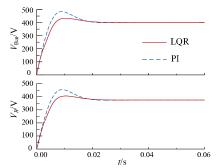
TAB变换器电路启动时两种控制方法下各端口电压变化情况如图6所示。图中可见, TAB变换器启动时各端口电压在LQR控制与PI解耦控制下经过约0.03 s后达到稳态, 但LQR控制下电压超调量明显较小, 端口2最大超调量为28 V, 端口3最大超调量为18 V; PI解耦控制下端口2最大超调量为85 V, 端口3最大超调量为72 V, 显然LQR控制在TAB电路启动时具有更好的控制效果。
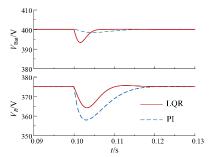
TAB变换器负载突变时两种控制方法下各端口电压变化情况如图7所示。电路处于稳态时, 在t= 0.1 s时刻, 端口3负载R由30 Ω 突变为15 Ω , 由图7可知, 在PI解耦控制下各端口电压经过约0.02 s后再次达到稳态, 在LQR控制下各端口电压经过约0.013 s后再次达到稳态, LQR控制的响应速度较快, 但在PI解耦控制下, 由于在控制中加入了前馈解耦矩阵, 故端口2电压受到端口耦合的影响较小, 最大超调量为2.6 V, 端口3最大超调量为18.6 V; LQR解耦控制下端口2最大超调量为6.6 V, 为端口2电压参考值的1.65%, 在可接受的偏差范围之内, 端口3最大超调量为11.8 V, 比PI解耦控制下的电压偏差更小, 从整体上看LQR控制具有更好的动态响应能力。
针对TAB变换器在解耦矩阵变化较大时控制效果较差的问题, 提出基于线性二次型(LQR)最优的控制策略。通过电路等效变换建立了TAB变换器的状态空间模型, 设计了LQR控制器, 并对比传统的PI解耦控制对电路工况突变的情况进行了仿真。结果表明, 与传统的PI解耦控制相比, LQR控制在TAB电路启动时超调量小, 具有更好的控制效果, 在端口负载突变时超调量相差不大, 但具有更快的响应速度, 在工况变化时具有更好的动态响应能力。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|