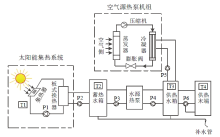
太阳能-热泵双水箱复合供暖系统组成及原理如图1所示。系统由太阳能集热子系统、热泵系统、蓄热水箱、供热水箱及供暖末端系统组成。在太阳光照射强度不充分时, 系统优先使用太阳能, 热泵机组可通过对供热水箱中的水加热进行供热。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 太阳能-热泵复合供暖系统组成及原理Fig. 1 Composition and principle of solar-heat pump composite heating system

根据室外太阳辐射状况及气候不同, 系统采用温差循环控制, 制热时可分为三种模式。第一种, 太阳能集热系统与水源热泵联合供热：当天气晴朗, 太阳能充足时, 集热器将太阳能转换为热能, 水泵P1、P2开启, 将热量储存到储热水箱至温度达到某一设定值时, 水源热泵启动, P3、P4开启, 水源热泵从储热水箱中吸收热量至供热水箱中, 向室内末端进行供暖。第二种, 空气源热泵独立供热：无光照或雨雪等极端条件时, 太阳能集热系统停止运行, 水源热泵关闭。水泵P5开启, 空气源热泵吸收空气中热量至供热水箱中, 通过供热水箱向室内末端进行供暖。第三种, 太阳能集热系统 + 水源热泵 + 空气源热泵供暖模式：在多云或太阳光照不足时, 太阳能集热系统和水源热泵联合供热无法满足供热需求时, 空气源热泵开始进行辅助制热, 其工作方式是模式1和模式2相结合。上述三种运行模式通过不同阀门之间的切换可实现运行模式的自主转换, 满足太阳能系统与热泵系统之间的结合与匹配, 系统可充分利用太阳能, 以满足供暖期各种气候条件的需要。

2.1.1 空气源热泵

在复合供暖系统中, 空气源在运行过程通过吸收空气中的热量对供热水箱中的水进行加热, 在该过程中消耗一定的功。空气源热泵制热时能量平衡方程如下：

$ Q_{\mathrm{e}}=Q_{\mathrm{h}}-P_{\mathrm{com}}$ (1)

空气源热泵制热性能系数（coefficient of performance, COP）为：

$ \varepsilon_{\mathrm{a}}=\frac{Q_{\mathrm{h}}}{P_{\mathrm{b}}+P_{\mathrm{con}}+P_{\mathrm{com}}}$ (2)

式中：$ Q_{\mathrm{e}}$为热泵制冷剂在热源侧的吸热量, kJ/h; $ Q_{\mathrm{h}}$为空气源热泵机组制热量, kJ/h; $ P_{\mathrm{com}}$为热泵机组压缩机的额定功率, kJ/h; $ P_{\mathrm{b}}$为风机额定功率, kJ/h; $ P_{\text {con }}$为控制器额定功率, kJ/h。

2.1.2 平板集热器

太阳能平板集热器在集热过程中会损失一部分能量, 由能量守恒定律, 该过程热平衡方程为^[13]：

$ Q=F_{\mathrm{R}} A_{\mathrm{c}}\left[I_{\mathrm{t}}(\tau \alpha)_{\mathrm{e}}-U_{\mathrm{L}}\left(T_{\mathrm{i}}-T_{\mathrm{a}}\right)\right]$ (3)

式中：$ Q$为太阳能集热器有效得热量, W; $ F_{\mathrm{R}}$为太阳能集热器转移因子; $ A_{c}$为太阳能集热器面积, m²; $ I_{\mathrm{t}}$为倾斜面总辐照度, W/m²; $ (\tau \alpha)_{\mathrm{e}}$为玻璃盖板透射比与吸热板吸收比之积; $ U_{\mathrm{L}}$为太阳能集热器总损失热系数, W/(m²∙ K); $ T_{\mathrm{i}}$为进口温度, ℃; $ T_{\mathrm{a}}$为环境温度, ℃。

2.1.3 倾斜面太阳辐照量

系统选用平板型集热器时, 投射到集热器表面上的太阳能总辐照量包括直射辐射、散射辐射及地面的反射辐射三部分。

$ I_{\mathrm{t}}=I_{\mathrm{b}} R_{\mathrm{b}}+I_{\mathrm{d}}\left(\frac{1+\cos \beta}{2}\right)+\left(I_{\mathrm{b}}+I_{\mathrm{d}}\right) \rho_{\mathrm{G}}\left(\frac{1-\cos \beta}{2}\right)$ (4)

式中：$ I_{\mathrm{b}}$为水平面上的太阳总辐射强度, W/m²; $ I_{\mathrm{d}}$为水平面上的散射辐射强度, W/m²; β 为太阳能集热器倾角, ° ; $ \rho_{\mathrm{G}}$为地表反射率; $ R_{\mathrm{b}}$为倾斜面上直射辐射修正因子。

若太阳能集热器向南安置, 此时, 集热器倾斜面上的直射辐射修正因子按下式进行计算：

$ R_{\mathrm{b}}=\frac{\cos (\varphi-\beta) \cos \delta \cos \omega+\sin (\varphi-\beta) \sin \delta}{\cos \varphi \cos \delta \cos \omega+\sin \varphi \sin \delta}$ (5)

式中：$ \omega$为太阳时角, ° ; $ \delta$为当地太阳赤纬角, ° ; $ \varphi$为当地纬度, ° 。

太阳能集热器迁移因子计算公式为：

$ F_{\mathrm{R}}=\frac{m_{\mathrm{c}} \mathcal{C}_{p}}{A_{\mathrm{c}} U_{\mathrm{L}}}\left[1-\exp \left(-\frac{U_{\mathrm{L}} F^{\prime} A_{c}}{m_{\mathrm{c}} \mathcal{C}_{p}}\right)\right]$ (6)

式中：$ m_{\mathrm{c}}$为太阳能集热器循环流量, kg/s; $ c_{p}$为水的比热容, kJ/(kg∙ ℃); $ F^{\prime}$为太阳能集热器效率因子。

集热器效率是指液体通过集热器的吸热总量与集热器表面太阳辐射总量的比, 其数学模型为^[14]：

$ \eta=F_{\mathrm{R}}(\tau \alpha)_{\mathrm{e}}-F_{\mathrm{R}} U_{\mathrm{L}} \frac{T_{\mathrm{i}}-T_{\mathrm{a}}}{I_{\mathrm{t}}}-F_{\mathrm{R}} U_{\mathrm{L} / \mathrm{T}} \frac{\left(T_{\mathrm{i}}-T_{\mathrm{a}}\right)^{2}}{I_{\mathrm{t}}}$ (7)

式中：$ F_{\mathrm{R}}(\tau \alpha)_{\mathrm{e}}$为截距效率; $ F_{\mathrm{R}} U_{\mathrm{L}}$为斜率效率, W/(m²∙ K); $ F_{\mathrm{R}} U_{\mathrm{L} / \mathrm{T}}$为曲率效率, W/(m²∙ K²)。

2.1.4 蓄热水箱

在供热系统中, 在太阳能不足的情况下, 蓄热水箱为水源热泵提供热源, 是整个系统中的重要部件。多节点温度分层水箱模型被应用于蓄热水箱^[7]。在模型中, 假设水箱中的水被分成若干层, 每层温度分布均匀, 但不同层间有温差, 对于节点i, 其能量平衡方程^[15]如下：

$ \begin{array}{c} M_{i} c \frac{\mathrm{d} T_{i}}{\mathrm{~d} t}=\alpha_{i} m_{\mathrm{n}} c\left(T_{1}-T_{i}\right)+\beta_{i} m_{\mathrm{L}} c\left(T_{2}-T_{i}\right)+ \\ (U A)_{i}\left(T_{\mathrm{a}}-T_{i}\right)+K \end{array}$ (8)

$ g_{i}> 0$时 $ i=1, \cdots, N \cdots K=\gamma_{i}\left(T_{i-1}-T_{i}\right) c_{p}$

$ g_{i}< 0$时 $ i=1, \cdots, N \cdots K=\gamma_{i}\left(T_{i}-T_{i+1}\right) c_{p}$

式中：$ M_{i}$为第i个节点水层的质量, $ \mathrm{kg} / \mathrm{s}$; c为液体的比热容, kJ/(kg∙ ℃); $T_1$为热源入口温度, ℃; $T_2$为补水侧流入水箱的水的温度, ℃; $(U A)_{i}$为对应蓄热水箱的热损失系数, W/℃; $\gamma_{i}, g_{i}$为与第i个节点相邻的温度节点间的热、质交换控制参数; $m_{\mathrm{n}}, m_{\mathrm{L}}$为板式换热器二次侧、水箱侧的质量流量, $\mathrm{kg} / \mathrm{s}$; $T_{i}$为第i个节点的水温, ℃; $\alpha_{i}, \beta_{i}$为板式换热器、蓄热水箱的流量控制参数。

2.1.5 水源热泵

在复合供暖系统中, 水源热泵通过吸收热源侧储热水箱中的热量, 经过热泵进一步做功后, 对供热水箱中的水进行加热。水源热泵制热工况下吸热量如下：

$Q_{\text {absorded }}=Q_{\text {heating }}-P_{\text {heating }}$ (9)

水源热泵的制热性能系数为：

$\varepsilon_{\mathrm{w}}=\frac{Q_{\text {heading }}}{P_{\text {heading }}}$ (10)

式中：$Q_{\text {absorded }}$为热泵热源侧吸热量, kW; $Q_{\text {heating }}$为水源热泵制热量, kW; $P_{\text {heating }}$为热泵制热功率, kW。

2.2.1 系统参数

太阳能-热泵复合供暖系统以太阳能系统为主, 热泵系统为辅。系统各部件根据《太阳能集中热水系统选用与安装》^[16]、《民用建筑节水设计标准》^[17]设计参数, 对模型中主要组件初始参数设置见表1。

表1

Table 1

表1(Table 1)

表1 仿真模型部件参数设定 Table 1 Parameters setting of simulation model components 部件 参数 数值 太阳能平板集热器 面积/m2 倾角/(° ) 375 50 供热水箱 容积/m3 保温系数/[W/(m2∙ K)] 4 3 循环水泵 额定流量/(kg/s) 0.1 蓄热水箱 容积/m3 保温系数/[W/(m2∙ K)] 5 3

表1 仿真模型部件参数设定 Table 1 Parameters setting of simulation model components

2.2.2 系统模型

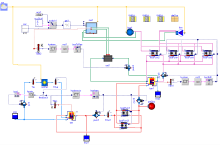
系统由Dymola平台通过各个模块的组合搭建实现系统仿真, 其组件有集热器模型、气象数据模型、水箱模型、热泵模型及水泵模型, 其仿真模型可视化界面如图2所示, 结合系统的运行模式对其进行供热模拟。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 太阳能-热泵复合供暖系统仿真模型Fig. 2 Simulation model of solar-heat pump combined heating system

2.3.1 实验装置

实验在宁夏固原市彭阳县新集乡卫生院进行, 供暖建筑是宿舍楼和门诊楼, 供暖面积为3 000 m², 宿舍楼共2层, 建筑结构采用混砖结构, 无内外保温, 无遮阳, 建筑周围均与大气接触。门诊楼共3层, 建筑结构为框架结构。系统的实验装置主要包括平板太阳能集热器、热泵热水机组及水箱等, 系统实物图如图3所示。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 实验平台现场图：（a）空气源热泵机组; （b）蓄热水箱; （c）平板太阳能集热器Fig. 3 Field diagram of the experimental platform: (a) air source heat pump unit; (b) heat storage tank; (c) flat plate solar collector

2.3.2 实验设备及测试仪器

实验测试主要对系统的温度、电量等参数进行测量, 将采集到的实时数据记录并存储到物联网大数据平台。实验过程中室内温度测点放置在距离供暖系统最远的宿舍楼二层最西边的房间, 温度测点位置与墙体水平距离大于1 m, 距离地面2 m。实验时间为2021年供暖季11月1日至次年3月1日, 太阳能-热泵双水箱复合供暖系统主要设备及型号参数见表2, 实验测试过程中所需测试仪器见表3。

表2

Table 2

表2(Table 2)

表2 实验主要设备 Table 2 Main experimental equipment 系统设备 型号或参数说明 平板太阳能集热器 P-G/0.6-T/L-HM-2.83-1, 集热面积3 m3, 循环工质为防冻液 高温水源热泵 YCTGS-DKFXRS-100II, 额定功率25 kW, 制热量90 kW 空气源热泵 YGFG-DKFXRS-100II, 额定制热量75 kW 空气源热泵循环泵 扬程11 m, 流量86 m3/h, 功率7.5 kW 水源热泵循环泵 扬程17 m, 流量52.2 m3/h, 功率5.5 kW 蓄热水箱 方型不锈钢制开式水箱体积5 m3

表2 实验主要设备 Table 2 Main experimental equipment

表3

Table 3

表3(Table 3)

表3 实验测试主要仪器 Table 3 Main instruments for experimental testing 仪器 型号 量程 精度 温度传感器 PT100 -60 ~ 260 ℃ 0.15 ℃ 压力变送器 PCM300 0 ~ 40 kPa 0.5% 涡街流量传感器 SLDLB 15 ~ 220 m3/h 1级 三项多功能电能表 DTSD1352 3 × 10(80) A 0.2%

表3 实验测试主要仪器 Table 3 Main instruments for experimental testing

为验证仿真模型的可靠性, 现以1月13日为典型日, 将该天的气象数据加载至系统仿真模型进行模拟, 选取系统中运行过程中的储热水箱、供热水箱温度以及集热器温度的实验数据与仿真数据进行对比, 如图4所示。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 模拟与测试结果对比图：（a）蓄热水箱温度; （b）供热水箱温度; （c）集热器温度Fig. 4 Comparison of simulation and test results: (a) heat storage tank temperature; (b) heating water tank temperature; (c) collector temperature

由图4可知, 该仿真模型模拟数据与系统实际实验数据的变化规律基本保持一致。储热水箱实际平均温度为17.2 ℃, 模拟值的平均温度为15.6 ℃, 误差率为9.3%。集热器温度实际平均值为26.7 ℃, 模拟值的平均温度为23.6 ℃, 误差率为11.6%。供热水箱实际平均温度为59.3 ℃, 模拟值的平均温度为57.6 ℃, 误差率为2.9%。综上, 仿真模型误差在8%左右, 说明所建立仿真模型的准确性高。

全生命周期成本（life cycle costing, LCC）是设备在其整个生命期限内（从设计、研发、生产、使用和维修到报废处理）所需的全部资金, 以确保其正常运行和发挥功能^[12]。选择太阳能-热泵双水箱复合供暖系统的目标函数为全生命周期成本^[14]：

$\min \left(C_{\mathrm{LCC}}\right)=\min \left(C_{\mathrm{CRF}} \cdot n \cdot C_{\mathrm{in}}+C_{\mathrm{om}}-C_{\mathrm{rc}}\right)$ (11)

式中：$C_{\text {in }}$为设备初投资, 元; $C_{\text {om }}$为设备运行资金, 元; $C_{\text {CRF }}$为资本回收系数; n为设备年限, 15 a; $C_{\text {rc }}$为设备回收时的剩余价值, 元。

设备初投资为：

$C_{\text {in }}=C_{\text {ashp }} \cdot P_{\text {ashp }}+C_{\text {solar }} \cdot A_{\mathrm{c}}+C_{\text {tank }} \cdot V_{\text {tank }}+C_{\text {wshp }} \cdot P_{\text {wshp }}$ (12)

式中：$C_{\text {ashp }}$为空气源热泵单位输入功率成本, 元/kW; $C_{\text {solar }}$为太阳能集热器面积的单位成本, 元/m²; $C_{\text {tank }}$为蓄热水箱容积的单位成本, 元/kW; $C_{\text {wshp }}$为水源热泵输入功率的单位成本, 元/kW; $ P_{\text {ashp }}$为空气源热泵输出功率, kW; $A_c$为集热器面积, m²; $ V_{\text {tank }}$为蓄热水箱容积, m³; $ P_{\text {whp }}$为水源热泵的输入功率, kW。

系统的运行费用包括在供热过程中消耗的电量费用和设备维护费用, 其数学表达式为：

$ C_{\mathrm{om}}=C_{\mathrm{e}} \cdot \sum_{n=1}^{n} W_{\mathrm{p}}+C_{\mathrm{in}} \cdot \psi$ (13)

式中：$ W_{\mathrm{P}}$为系统年耗电量, kW∙ h; $ \psi$设备维护费用系数, 一般取值为设备初投资的2%^[14]; $ C_{\mathrm{e}} j$为当地电价, 元/(kW∙ h)。

资本回收系数计算公式如下：

$ C_{\mathrm{CRF}}=\frac{i(1+i)^{n}}{(1+i)^{n}-1}$ (14)

式中：i为利率, 取8%^[18]。设备回收对应的剩余价值一般取初投资的3% ~ 5%^[19]。其数学表达式为：

$ C_{\mathrm{rc}}=C_{\text {in }} \cdot r$ (15)

式中：r为剩余价值在初始投资中的占比, 取4%^[19]。

优化变量的选取是优化问题中的关键部分, 其不同会导致最终优化结果具有较大的差异, 因此优化变量的合理选取至关重要。在太阳能-热泵复合系统中, 系统性能会受到多个变量的影响, 这些变量相互耦合, 当这些变量不同组合时, 系统性能也有所差异。

选取系统中集热器倾角、热泵功率、水箱容积、太阳能集热器面积4个重要参数作为优化变量。在模型优化中, 设定太阳能集热器面积时, 要确保在供暖季内太阳能保证率的范围在0% ~ 100%。根据文献[20], 在太阳能供暖系统中, 集热器的采光面积所对应的蓄热水箱容积按50 ~ 150 L/m²范围选取。太阳能集热器的安装倾角在当地纬度的 ± 10° 范围内进行选择。在冬季最冷月的工况下, 空气源热泵机组按照满足供暖的需求, 根据其设计工作时间所需制热量确定热泵功率^[21]。由于所选的空气源热泵仅用于供热, 因此其容量仅与采暖热负荷有关。

3.3.1 能量平衡约束

能量平衡约束表示热量的供需关系, 供热系统要满足任意时刻的能量平衡, 因此在$ \tau$时刻系统应满足：

$ \begin{array}{c} Q_{\mathrm{HX}}(\tau)+Q_{\mathrm{HP} \beta}(\tau)+Q_{\text {ass }}(\tau)-Q_{\mathrm{h}}(\tau)- \\ Q_{\mathrm{sX}}(\tau)-Q_{\text {loss }}(\tau)=0 \end{array}$ (16)

式中：$ Q_{\mathrm{HX}}(\tau)$为集热系统在τ 时刻的供热量, W; $ Q_{\mathrm{HP} \beta}(\tau)$为热泵机组在τ 时刻的制热量, W; $ Q_{\mathrm{ass}}(\tau)$为辅助热源在τ 时刻的制热量, W; $ Q_{\mathrm{h}}(\tau)$为建筑在τ 时刻的热需求量, W; $ Q_{\mathrm{sx}}(\tau)$为蓄热水箱在τ 时刻的蓄热量, W; $ Q_{\text {loss }}(\tau)$为在τ 时刻水箱向外界损失的热量, W。

3.3.2 初始约束

假设在系统运行初期, 水箱水温取45 ℃, 辅助热源处于关闭状态。

$ \left\{\begin{array}{l} T_{\mathrm{sx}}(\tau=1)=45 \\ S_{\mathrm{ass}}(\tau=1)=0 \\ \frac{1}{2} \cdot \frac{Q_{\mathrm{h}, \max }}{\varepsilon_{\mathrm{a}}} \leq P_{\mathrm{ashp}} \leq \frac{Q_{\mathrm{h}, \max }}{\varepsilon_{\mathrm{a}}} \\ 0 \leq A_{\mathrm{co}} \leq A_{f=1} \\ 0.5 \leq V_{\mathrm{sx}} \leq 0.25 A_{f=1} \\ 40 \leq T_{\min } \leq 45 \\ 45 \leq T_{\max } \leq 55 \\ 40^{\circ} \leq \beta \leq 50^{\circ} \\ 0< n \leq 15 \end{array}\right.$ (17)

式中：$ T_{\mathrm{sx}}$为水箱温度, ℃; $ S_{\mathrm{ass}}$为辅助热源启停状态, 关闭为0, 开启为1; $ Q_{\mathrm{h}, \max }$为供暖期内建筑在每小时热负荷的最大值, kW/h; $ A_{c o}$为太阳能集热器设计面积, m²; $ A_{f=1}$为由规范标准计算, 当太阳能保证率为100%得出的集热器面积, m²; $ V_{\mathrm{sx}}$为水箱容积, m³; $ T_{\min }$为热泵启停最低温度, ℃; $ T_{\max }$为热泵启停最高温度, ℃。

已有的文献多数利用Hooke-Jeeves算法进行多参数优化^[22]。由于Hooke-Jeeves算法会陷入部分最优, 即优化结果对定义的初始值依赖性较强。然而, 考虑到复合供暖系统的优化问题归于非线性、不可微和多极值问题, 则使用其他方法进行求解时, 会更困难, 但通过遗传算法（genetic algorithm, GA）进行求解会得到较好的结果^[19]。

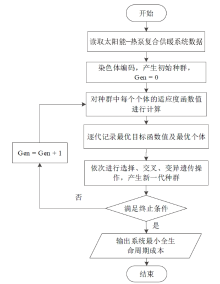
遗传算法是通过模拟自然界中生物的进化过程而形成的一种可搜索最优解的算法, 其与传统算法不同, 具有很高的鲁棒性和广泛性, 目前在组合优化、图像处理和遗传编码等多个领域已被应用^[23], 利用遗传算法结合所建模型进行优化计算, 流程如图5所示。

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 遗传算法优化计算流程Fig. 5 Genetic algorithm to optimization calculation flow

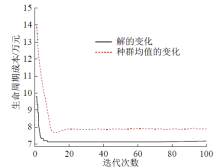
从图6遗传算法优化过程中可以看出, 迭代至10次时已经基本收敛, 当迭代计算为100次时已全部收敛, 此时生命周期成本最低是717 528元, 收敛时对应的最佳变量分别是太阳能集热器面积为356 m²、集热器最佳倾角为43° 。

图6

Fig. 6

	Figure Option ViewDownloadNew Window
	图6 遗传算法优化过程Fig. 6 Genetic algorithm optimization process

4.2.1 优化前后对比分析

按4.1优化结果, 系统中变量优化前后对比见表5, 系统优化后运行能耗可节省52 kW∙ h, 比优化前节省6.9%, 系统COP提高10.3%, 且水箱的平均温度提高3.8%, 说明该系统经优化后, 结构可靠且具有较好的节能效果。

表5

Table 5

表5(Table 5)

表5 系统优化前后参数对比 Table 5 Comparison of parameters before and after optimization 参数 耗电量/(kW∙ h) 平均温度/℃ 系统平均COP 空气源热泵功率/kW 集热器面积Ac/m2 集热器倾角/(° ) 优化前 757.2 52.70 2.9 37 375 50 优化后 705.0 54.71 3.2 35 356 43 变化率 -6.9% +3.8% +10.3% -5.4% -5.3% -14%

表5 系统优化前后参数对比 Table 5 Comparison of parameters before and after optimization

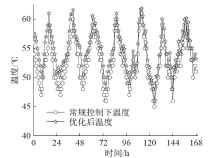
为验证寻优算法结果的有效性, 优化前系统运行控制策略采用温差循环控制。在系统容量一定的前提下, 以宁夏地区为例选取最冷月1月为模拟对象, 为避免存在典型日的随机性和不准确性, 选择1月8日至1月14日连续7天的运行情况进行模拟。运行优化前后, 水箱的平均温度如图7所示, 由图可知优化前最高温度为59 ℃, 最低温度为45 ℃; 优化后水箱最高温度为61 ℃, 最低温度为46 ℃, 运行优化后水箱温度均高于优化前。

图7

Fig. 7

	Figure Option ViewDownloadNew Window
	图7 运行优化前后水箱逐时水温Fig. 7 Tank-by-tank water temperature before and after operation optimization

4.2.2 系统节能效益分析

节能性是指复合供暖系统相对于传统燃煤供暖方式所消耗的一次能源节能率。通过最大限度地利用太阳能, 降低复合供暖系统的运行能耗, 并将优化后的系统节能效果和优化前及传统供暖系统进行对比, 并进行节能性评价。将不同供暖方式的能源消耗量转换为标准煤的形式进行对比, 可使节能效果更加直观。计算公式如下：

$ m=\frac{Q}{q_{j} \cdot \eta}$ (18)

式中：m为耗煤量, t; Q为一次能源消耗量, MJ; $ q_{j}$为不同能源燃料折算为标准煤后的热值; $ \eta$为燃煤锅炉效率, 取60%。

以宁夏某地区复合供暖系统实际工程为对象, 2021— 2022年度系统供暖季总能耗为168 784 kW∙ h, 由式（18）分别计算得到, 系统总耗电量换算为标准煤是34.6 t; 优化后, 系统总能耗为166 312 kW∙ h, 换算为标准煤是34 t。而该项目采用传统燃煤供暖方式时, 每年所需标准煤平均在45 t左右。

因此, 在整个供暖期中, 优化后的复合供暖系统比优化前的系统更节省能源, 节能率为1.8%; 而相比于传统燃煤锅炉, 优化后的系统更加节省能源消耗, 节能率为24.4%。由此可见, 优化后系统的节能性具有明显提升。

4.2.3 环保效益分析

环保效益是由供热系统排放的污染物来反映, 传统燃煤供暖排放的污染物会对周围环境造成严重的污染。本研究提出的太阳能-热泵双水箱复合供暖系统可同时减少污染物SO₂、CO₂、NO_x及烟尘等排放。该系统污染物减排量数学公式如下：

$ m_{\mathrm{p}}=B \cdot F_{\mathrm{r}}$ (19)

式中：$ m_{\mathrm{p}}$为各污染物排放量, t; B为供热系统所需燃料的消耗量, t; $ F_{\mathrm{r}}$为标准煤的污染物排放因子。

污染物的排放因子见表6^[25]。

表6

Table 6

表6(Table 6)

表6 污染物排放因子[25] Table 6 Pollutants emission factors[25] 污染物 Fr SO2 0.074 CO2 2.418 NOx 0.037 烟尘 0.680

表6 污染物排放因子[25] Table 6 Pollutants emission factors[25]

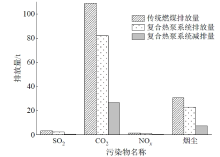
系统优化后在整个供暖季的节能量换算为标准煤是11 t。由式（19）计算得到传统燃煤和复合热泵系统各类污染物的排放量及减排量如图8所示。

图8

Fig. 8

	Figure Option ViewDownloadNew Window
	图8 两种供暖方式供暖季污染物排放量Fig. 8 Pollutants emission during the heating season for both types of heating

由图8可知, 此次建立的太阳能-热泵双水箱复合供暖系统减少了有害气体SO₂、CO₂、NO_x及烟尘的排放, 其减排量分别为0.82、26.6、0.41、7.48 t, 与传统燃煤锅炉相比, 减碳效果显著, 环保效益大大提升。