引用本文
戴春江, 李帅旗, 李江峰, 吕杰, 宋文吉, 冯自平. 车用跨临界CO2空调系统变工况㶲分析 [J]. 新能源进展, 2024,12(4): 388-399
DAI Chunjiang, LI Shuaiqi, LI Jiangfeng, LÜ Jie, SONG Wenji, FENG Ziping. Exergy Analysis of Trans-Critical CO2 Air Conditioning System for Vehicle [J]. ADV NEW RENEWABLE EN, 2024,12(4): 388-399.  
Doi: 10.3969/j.issn.2095-560X.2024.04.004
Permissions
Copyright©2024, 《新能源进展》编辑部
版权所有 © 《新能源进展》编辑部
车用跨临界CO2空调系统变工况㶲分析
戴春江1,2, 李帅旗2,†, 李江峰3, 吕杰2, 宋文吉1,2, 冯自平1,2
1.中国科学技术大学 能源科学与技术学院,广州 510640
2.中国科学院广州能源研究所,广州 510640
3.比亚迪汽车工业股份有限公司,广东 深圳 518118
† 通信作者：李帅旗,E-mail：lisq@ms.giec.ac.cn

作者简介：戴春江（2000-）,男,硕士研究生,主要从事汽车热泵空调系统研究。李帅旗（1991-）,男,博士,工程师,主要从事先进热泵技术研究及应用研究。

收稿日期: 2023-12-18 修订日期:: 2024-2-11
基金项目: 重庆市城市建设科技计划项目（城科字2023第2-9号）
摘要

为了确定影响车用跨临界CO2空调系统性能的因素,构建了车用跨临界CO2空调系统的仿真模型,并利用仿真数据对系统及各部件进行了热力学分析。研究了不同的压缩机转速、气体冷却器进风风速、气体冷却器进风温度、蒸发器进风量和蒸发器进风温度对系统㶲损、㶲效率和各部件相对㶲损的影响。结果表明：在所研究的工况范围内,压缩机转速、气体冷却器进风风速和温度对系统㶲损影响较大;系统最大的㶲损来自膨胀阀,在各工况下平均占系统总㶲损的36.54%,其次分别是气体冷却器、压缩机和蒸发器,分别占系统总㶲损的24.24%、20.47%和18.81%;系统的总㶲损随压缩机转速增加和气体冷却器进风温度升高而增大,随气体冷却器进风风速增加和蒸发器进风温度升高而减小,随蒸发器进风风速的增加先减后增;系统的㶲效率随压缩机转速增加和蒸发器进风温度升高而降低,随气体冷却器进风风速增加和风温的升高而升高,随蒸发器进风风速先增后减。

关键词: 跨临界CO2; 车用空调; 㶲损; 㶲效率
中图分类号:TB61+1;TK123 文献标识码:A 文章编号:2095-560X（2024）04-0388-12
Exergy Analysis of Trans-Critical CO2 Air Conditioning System for Vehicle
DAI Chunjiang1,2, LI Shuaiqi2,†, LI Jiangfeng3, LÜ Jie2, SONG Wenji1,2, FENG Ziping1,2
1. School of Energy Science and Engineering, University of Science and Technology of China, Guangzhou 510640, China
2. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China
3. BYD Auto Industry Company Limited, Shenzhen 518118, Guangdong, China
Abstract

To determine the factors affecting the performance of the vehicular trans-critical CO2 air-conditioning system, the simulation model of trans-critical CO2 air-conditioning system for vehicle is established, and the thermodynamic analysis of the system and its components is carried out by using the simulation data. This paper studies the effects of variable compressor speed, air inlet speed of gas cooler, air inlet temperature of gas cooler, air inlet volume of evaporator, and air inlet temperature of evaporator on exergy loss and efficiency of the system and relative loss of each component. The results show that the compressor's rotating speed, air inlet velocity and temperature greatly influence the system's exergy loss. The maximum exergy loss of the system comes from the expansion valve, which accounts for 36.54% of the total exergy loss of the system on average under each working condition, followed by the gas cooler, compressor, and evaporator, which accounts for 24.24%, 20.47% and 18.81% of the total exergy loss of the system respectively. The total exergy loss of the system increases with the increase of the compressor speed and the air inlet temperature of the gas cooler, decreases with the increase of the air inlet velocity of the gas cooler and the air inlet temperature of the evaporator, decreases first and then increases with the increase of the inlet air speed of the evaporator. The exergy efficiency of the system decreases with the increase of the compressor speed and the inlet air temperature of the evaporator, and increases with the increase of the inlet air speed and temperature of the gas cooler, and increases first and then decreases with the inlet air speed of the evaporator.

Key words: trans-critical CO2; air conditioning for vehicle; exergy loss; exergy efficiency
0 引言

近年来, 由于制冷剂泄漏导致的全球变暖问题逐渐受到重视, 《蒙特利尔议定书》及其修正案已经被全球大多数国家接受, 将逐渐限制氢氯氟烃制冷剂的使用[1]。使用对环境友好的天然制冷剂逐渐成为了研究热点, 其中CO2由于其绿色环保、价格低廉、无毒不燃、密度高、良好的流动性和传热特性受到制冷行业广泛关注[2]。

20世纪90年代, LORENTZEN等[3]率先提出将跨临界CO2空调系统运用于汽车空调, 随后大量学者针对CO2制冷剂在汽车空调系统中的应用展开了广泛研究。刘洪胜等[4]研究了CO2充注量对汽车空调性能的影响, 发现存在使系统性能系数（coefficient of performance, COP）最大的CO2充注量。KAUF[5]和LIAO等[6]通过数值模拟研究发现存在最优排气压力使得系统COP最大, 并分析了影响最优排气压力的因素。KIM等[7]对跨临界CO2汽车空调进行了实验研究, 发现在最佳气体冷却器压力下, 系统在变工况下均具有较好的制冷性能。对于跨临界CO2循环的优化, CHO等[8]和BAEK等[9]研究了带中间补气的跨临界CO2循环, 发现带补气的跨临界CO2循环拥有更高的制冷、制热性能。董丽玮等[10]研究了带引射器的跨临界CO2机械过冷热泵系统, 发现引射器可以减少系统能量损失, 提升系统COP。方健珉等[11]研究了回热器对汽车跨临界CO2系统的影响, 结果表明回热器的使用可以有效提高系统性能, 同时会引起压缩机压比增大和排气温度的升高。

蒸汽压缩热泵空调系统的评价一般是基于能耗分析的结果, 对于跨临界CO2循环的热力学分析, YANG等[12]对比了带节流阀与膨胀机的跨临界CO2制冷循环, 研究表明带膨胀机的跨临界CO2制冷循环COP平均比带节流阀的高33%。然而, 与能耗分析相比, 㶲分析方法作为能量品质和数量的有效评价方法, 能够更加准确地展示系统各部件的损耗情况, 已被广泛应用于各类热力循环系统中[13, 14, 15, 16], 可为热力系统的优化提供方向。

汽车空调不同于家用空调系统, 由于其空间可移动性决定了系统运行工况处于不断变化中, 跨临界CO2空调系统的制冷性能受外界环境影响较大, 当制冷性能不佳时将导致电动汽车续航里程下降。本文根据电动汽车空调系统构建跨临界CO2循环模型, 通过仿真研究变工况下系统的运行性能。利用仿真数据对车用跨临界CO2空调系统及其系统部件进行㶲分析, 探讨变压缩机转速、变气体冷却器进风风速、变气体冷却器进风温度、变蒸发器进风量和变蒸发器进风温度对系统㶲损和㶲效率及各部件相对㶲损的影响, 以期为电动汽车跨临界CO2空调系统的优化和设计提供参考。

1 模型建立

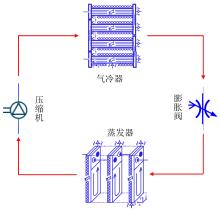
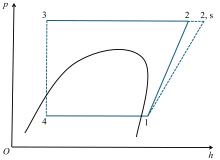
图1和图2分别展示了跨临界CO2循环热泵系统简图和压焓（p-h）图。系统主要由压缩机、气体冷却器、蒸发器和膨胀阀构成。

图1 跨临界CO2循环热泵系统简图Fig. 1 Diagram of trans-critical CO2 cycle heat pump system

图2 跨临界CO2循环图Fig. 2 Diagram of trans-critical CO2 cycle

1.1 压缩机模型

压缩机模型由等熵效率（η is）、容积效率（η v）、制冷剂流量（${{\dot{m}}_{\text{r}}}$）和压缩机耗功（Wcomp）所构成：

${{\eta }_{\text{is}}}=\text{0}\text{.9611}-\text{0}\text{.052}\frac{{{p}_{\text{dis}}}}{{{p}_{\text{suc}}}}$ (1)

${{\eta }_{\text{v}}}=\text{0}\text{.8882}-\text{0}\text{.04185}\frac{{{p}_{\text{dis}}}}{{{p}_{\text{suc}}}}$ (2)

${{\dot{m}}_{\text{r}}}={{\rho }_{1}}{{\eta }_{\text{v}}}V{{n}_{\text{com}}}$ (3)

${{W}_{\text{comp}}}=\frac{{{{\dot{m}}}_{\text{r}}}\left( {{h}_{2}}-{{h}_{1}} \right)}{{{\eta }_{\text{is}}}{{\eta }_{\text{me}}}}$ (4)

式中：pdis、psuc分别为压缩机的排气压力和吸气压力, MPa; ${{\dot{m}}_{\text{r}}}$为制冷剂质量流量, kg/s; ${{\rho }_{1}}$为压缩机入口制冷剂密度, kg/m3; V为压缩机的排量, cm3; ncom为压缩机的转速, r/min; Wcomp为压缩机耗功, kW; h1、h2分别为压缩机入口和出口的制冷剂焓值, kJ/kg; η me为压缩机机械效率, 取0.9。

1.2 换热器模型

对换热器中制冷剂的流动和换热进行了简化, 采用离散微元（空气/壁面、壁面和翅片以及制冷剂/壁面）进行建模。

对于换热器内部的制冷剂侧：

${{Q}_{\text{int, }i}}={{h}_{\text{int, }i}}{{A}_{\text{r, }i}}\left( {{T}_{\text{r, }i}}-{{T}_{\text{w, }i}} \right)+{{\dot{m}}_{\text{r}}}{{L}_{\text{vap}}}$ (5)

${{h}_{\text{int}}}=N{{u}_{\text{r}}}\frac{{{\lambda }_{\text{r}}}}{{{D}_{\text{r}}}}$ (6)

$N{{u}_{\text{r}}}=\frac{\left( f/\text{8} \right)\left( Re-\text{1000} \right)Pr}{\text{1}+\text{12}\text{.7}\sqrt{f/\text{8}}\left( P{{r}^{2/3}}-\text{1} \right)}$ (7)

$f=8{{\left\{ {{\left( \frac{8}{Re} \right)}^{12}}+{{\left[ {{\left\{ 2.45\ln \left[ \frac{1}{{{\left( {7}/{Re}\; \right)}^{0.9}}+0.27{{\varepsilon }_{0}}} \right] \right\}}^{16}}+{{\left( \frac{37530}{Re} \right)}^{16}} \right]}^{-{3}/{2}\; }} \right\}}^{{1}/{12}\; }}$ (8)

式中：Qint, i为换热器内部第i个微元段制冷剂的换热量, kW; hint, i为换热器第i个微元段内制冷剂与管壁的对流换热系数, kJ/(m2∙K); Ar, i为换热器内部第i个微元段制冷剂的换热面积, m2; Tr, i为第i个微元段内制冷剂的温度, ℃; Tw, i第i个微元段内换热器的壁温, ℃; Lvap为微元段内的制冷剂蒸发潜热, kJ/kg; hint为换热器内部制冷剂与管壁的对流换热系数, kJ/(m2∙K); Nur为制冷剂的努塞尔数; λ r为制冷剂的导热系数, kJ/(m∙K); Dr为换热器制冷剂侧特征长度, m; Re为雷诺数; Pr为普朗特数; f为阻力系数; ε 0为管壁的相对粗糙度, 取5 μm。

对于换热器外部的空气侧：

${{Q}_{\text{ext, }i}}={{\eta }_{\text{fin, }i}}{{h}_{\text{ext, }i}}{{A}_{\text{a, }i}}\left( {{T}_{\text{w, }i}}-{{T}_{\text{a, }i}} \right)$ (9)

${{h}_{\text{ext}}}={{\lambda }_{\text{a}}}N{{u}_{\text{a}}}/{{D}_{\text{a}}}$ (10)

$N{{u}_{\text{a}}}={{\eta }_{\text{fin}}}R{{e}^{\text{0}\text{.8}}}P{{r}^{\text{0}\text{.3}}}$ (11)

${{\eta }_{\text{fin}}}={{\lambda }_{\text{w}}}/{{e}^{\text{* }}}$ (12)

式中：Qext, i为换热器外部第i个微元段空气的换热量, kW; η fin, i为翅片第i个微元段的肋效率; hext, i为换热器第i个微元段内空气与管壁的对流换热系数, kJ/(m2∙K); Aa, i为换热器外部第i个微元段空气的换热面积, m2; Ta, i为第i个微元段内空气的温度, ℃; hext换热器外部空气与管壁的对流换热系数, kJ/(m2∙K); λ a为空气的导热系数, kJ/(m∙K); Da为换热器空气侧特征长度, m; Nua为空气的努塞尔数; η fin为翅片的肋效率; λ w为管壁的导热系数, kJ/(m∙K); e* 是几何参数。

换热器壁温：

$\frac{\text{d}{{T}_{\text{w, }i}}}{\text{d}t}=\frac{{{Q}_{\text{int, }i}}+{{Q}_{\text{ext, }i}}}{{{m}_{i}}{{C}_{p\text{, }i}}}$ (13)

式中：mi为换热器第i个微元段质量, kg; Cp, i为换热器第i个微元段比热容, kJ/(kg∙K)。

1.3 膨胀阀模型

制冷剂经过膨胀阀是等焓节流过程, 制冷剂质量流量计算如下：

${{\dot{m}}_{\text{r}}}={{C}_{\text{D}}}{{A}_{\text{C}}}\sqrt{\text{2}{{\rho }_{\text{exp}}}\text{ }\!\!\Delta\!\!\text{ }p}$ (14)

式中：CD为制冷剂通过膨胀阀的流量系数; AC为膨胀阀的流通截面积, m2; ρ exp为膨胀阀入口处制冷剂的密度, kg/m3; ∆ p为膨胀阀进出口的压差, MPa。

1.4 系统仿真平台

在AMESim软件中搭建了电动汽车跨临界CO2空调系统, 系统参数见表1, 仿真工况见表2。设定蒸发器出口过热度为5 ℃, 夏季的环境温度（T0）为室外气体冷却器进风温度, 压力为标准大气压。通过仿真得到了跨临界CO2系统分别在不同的压缩机转速、室外气冷器迎面风速、室外气冷器进风温度、空调箱进风量和不同空调箱进风温度下的运行数据。

表1 跨临界CO2空调系统参数 Table 1 Parameters of trans-critical CO2 air conditioning system
表2 跨临界CO2空调系统仿真工况 Table 2 Simulation conditions of trans-critical CO2 air conditioning system
2 㶲分析

在没有核效应、磁、电和表面张力的情况下, 物质流的㶲可表达为：

$\dot{E}={{\dot{E}}_{\text{k}}}+{{\dot{E}}_{\text{p}}}+{{\dot{E}}_{\text{ph}}}+{{\dot{E}}_{\text{ch}}}$ (15)

式中：${{\dot{E}}_{\text{k}}}$为动能㶲; ${{\dot{E}}_{\text{p}}}$为势能㶲; ${{\dot{E}}_{\text{ph}}}$为物理㶲; ${{\dot{E}}_{\text{ch}}}$为化学㶲。由于动能和势能的变化在制冷空调系统内造成的影响较小, 因此在热泵系统内可忽略动能㶲和势能㶲。化学㶲与系统的化学成分偏离其化学平衡有关, 制冷过程不涉及化学物质的混合和化学反应, 化学㶲可忽略不计。因此在整个制冷系统中只需要考虑其物理㶲。

对于单一工质的物理㶲$\psi $可表达为：

$\psi =\left( h-{{h}_{\text{0}}} \right)-{{T}_{\text{0}}}\left( s-{{s}_{\text{0}}} \right)$ (16)

式中：T0为环境温度; h和s为该工况点下工质的焓和熵; h0和s0为环境工况下工质的焓和熵。

系统内的进出口流动㶲的差异为系统的不可逆损失, 即㶲损, 可由㶲平衡方程表示：

$\text{ }\!\!\Delta\!\!\text{ }\dot{E}=\sum {{\dot{E}}_{\text{in}}}-\sum {{\dot{E}}_{\text{out}}}$ (17)

式中：${{\dot{E}}_{\text{in}}}$和${{\dot{E}}_{\text{out}}}$为通过系统进出口的质量和功所传递的总流动㶲, 将公式（17）展开可得：

$\begin{align} & \Delta \dot{E}=\sum\nolimits_{\text{in}}{{{{\dot{m}}}_{\text{r}}}\psi }-\sum\nolimits_{\text{out}}{{{{\dot{m}}}_{\text{r}}}\psi }+\sum\nolimits_{\text{in}}{{{{\dot{m}}}_{\text{a}}}\psi }- \\ & \ \ \ \ \ \ \ \ \sum\nolimits_{\text{out}}{{{{\dot{m}}}_{\text{a}}}\psi }+\sum\nolimits_{\text{in}}{{\dot{W}}}-\sum\nolimits_{\text{out}}{{\dot{W}}} \\ \end{align}$ (18)

式中：$\psi $为对应工质的物理㶲, kJ/kg; ${{\dot{m}}_{\text{a}}}$为空气质量流量, kg/m3; $\dot{W}$为流体的流动功, kW。

根据表达式（18）和热力学第一定律, 可得跨临界CO2系统各部件的㶲损失。

蒸发器：

$\begin{aligned} &\Delta\dot{E}_{\mathrm{e}}&& =\dot{m}_\mathrm{r}\left(\psi_4-\psi_1\right)+\dot{m}_\mathrm{ae}\left(\psi_\mathrm{in}-\psi_\mathrm{out}\right) \\ &&&=\begin{cases}\dot{m}_\mathrm{r}\left[\left(h_4-h_1\right)-T_0\left(s_4-s_1\right)\right]+\\\dot{m}_\mathrm{ae}\left[\left(h_\mathrm{aei}-h_\mathrm{aeo}\right)-T_0\left(s_\mathrm{aei}-s_\mathrm{aeo}\right)\right]\end{cases} \end{aligned}$ (19)

式中：${{\dot{m}}_{\text{ae}}}$为蒸发器中空气质量流量, kg/m3; h4为蒸发器入口处制冷剂焓值, kJ/kg; h1为蒸发器出口处制冷剂焓值, kJ/kg; s4为蒸发器入口处制冷剂熵值, kJ/(kg∙K); s1为蒸发器出口处制冷剂熵值, kJ/(kg∙K); haei为蒸发器入口处空气焓值, kJ/kg; haeo为蒸发器出口处空气焓值, kJ/kg; saei为蒸发器入口处空气熵值, kJ/(kg∙K); saeo为蒸发器出口处空气熵值, kJ/(kg∙K)。

压缩机：

$\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{comp}}}={{\dot{m}}_{\text{r}}}\left( {{\psi }_{\text{1}}}-{{\psi }_{\text{2}}} \right)+{{W}_{\text{comp}}}$ (20)

压缩机耗功：

${{W}_{\text{comp}}}={{\dot{m}}_{\text{r}}}\left( {{h}_{\text{2}}}-{{h}_{\text{1}}} \right)$ (21)

公式（20）可表达为：

$\begin{align} & \text{ }\!\!\Delta\!\!\text{ }{{{\dot{E}}}_{\text{comp}}}={{{\dot{m}}}_{\text{r}}}\left[ \left( {{h}_{\text{1}}}-{{h}_{\text{2}}} \right)-{{T}_{\text{0}}}\left( {{s}_{\text{1}}}-{{s}_{\text{2}}} \right) \right]+{{{\dot{m}}}_{\text{r}}}\left( {{h}_{\text{2}}}-{{h}_{\text{1}}} \right) \\ & \ \ \ \ \ \ \ \ \ \ ={{T}_{\text{0}}}\left( {{s}_{\text{2}}}-{{s}_{\text{1}}} \right) \\ \end{align}$ (22)

气冷器：

$\begin{aligned} &\Delta\dot{E}_{\mathrm{g}}&& =\dot{m}_\mathrm{r}\left(\psi_2-\psi_3\right)+\dot{m}_\mathrm{ag}\left(\psi_\mathrm{in}-\psi_\mathrm{out}\right) \\ &&&=\begin{cases}\dot{m}_\mathrm{r}\left[\left(h_2-h_3\right)-T_0\left(s_2-s_3\right)\right]+\\\dot{m}_\mathrm{ag}\left[\left(h_\mathrm{agi}-h_\mathrm{ago}\right)-T_0\left(s_\mathrm{agi}-s_\mathrm{ago}\right)\right]\end{cases} \end{aligned}$ (23)

式中：${{\dot{m}}_{\text{ag}}}$为气冷器中空气质量流量, kg/m3; h2为气冷器入口处制冷剂焓值, kJ/kg; h3为气冷器出口处制冷剂焓值, kJ/kg; s2为气冷器入口处制冷剂熵值, kJ/(kg∙K); s3为气冷器出口处制冷剂熵值, kJ/(kg· K); hagi为气冷器入口处空气焓值, kJ/kg; hago为气冷器出口处空气焓值, kJ/kg; sagi为气冷器入口处空气熵值, kJ/(kg∙K); sago为气冷器出口处空气熵值, kJ/(kg∙K)。

膨胀阀：

$\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{v}}}={{\dot{m}}_{\text{r}}}\left[ \left( {{h}_{\text{3}}}-{{h}_{\text{4}}} \right)-{{T}_{\text{0}}}\left( {{s}_{\text{3}}}-{{s}_{\text{4}}} \right) \right]$ (24)

膨胀阀为等焓节流过程, 其中：

${{h}_{\text{3}}}={{h}_{\text{4}}}$ (25)

公式（24）可表达为：

$\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{v}}}={{T}_{\text{0}}}\left( {{s}_{\text{4}}}-{{s}_{\text{3}}} \right)$ (26)

系统总㶲损为：

$\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{tot}}}=\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{e}}}+\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{comp}}}+\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{g}}}+\text{ }\!\!\Delta\!\!\text{ }{{\dot{E}}_{\text{v}}}$ (27)

系统各部件的相对㶲损为：

${{\delta }_{i}}=\frac{\text{ }\!\!\Delta\!\!\text{ }{{{\dot{E}}}_{i}}}{\text{ }\!\!\Delta\!\!\text{ }{{{\dot{E}}}_{\text{tot}}}}\times 100\%$ (28)

跨临界CO2循环的制冷㶲效率表示为：

$\begin{aligned} &\eta_{\mathrm{ex}}&& =\frac{\dot{E}_{\mathrm{gain}}}{\dot{E}_{\mathrm{pay}}}\times100\%=\frac{\left|\dot{m}_{\mathrm{ae}}\left(\psi_{\mathrm{out}}-\psi_{\mathrm{in}}\right)\right|}{\dot{m}_{\mathrm{r}}\left(h_{2}-h_{1}\right)}\times100\% \\ &&&=\frac{\left|\dot{m}_{\mathrm{ae}}\left[\left(h_{\mathrm{aeo}}-h_{\mathrm{aei}}\right)-T_{0}\left(s_{\mathrm{aeo}}-s_{\mathrm{aei}}\right)\right]\right]}{\dot{m}_{\mathrm{r}}\left(h_{2}-h_{1}\right)}\times100\% \end{aligned}$ (29)

式中：Egain、Epay分别为跨临界CO2循环制冷的收益㶲和投入㶲。

3 㶲分析结果与讨论
3.1 压缩机转速的影响

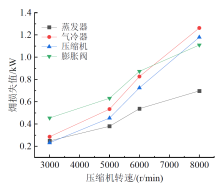
在表2所列的工况1下, 压缩机转速对系统各部件的㶲损失和相对㶲损的影响如图3、图4所示。由图3可知, 随着压缩机转速的增加, 系统各部件㶲损失均增大。其中气冷器与压缩机的㶲损失值受压缩机转速变化影响更大, 当压缩机转速由3 000 r/min逐渐增加至8 000 r/min时, 气冷器与压缩机的㶲损失值由0.286、0.232 kW增至1.262、1.180 kW, 分别增加了341.26%、408.62%。而膨胀阀与蒸发器的㶲损失值由0.455、0.249 kW增至1.110、0.698 kW, 仅增加了143.96%、180.32%。

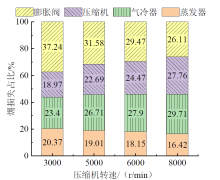图3 压缩机转速对系统各部件㶲损值的影响Fig. 3 The effects of compressor speed on the exergy loss of system components

图4 压缩机转速对系统各部件相对㶲损的影响Fig. 4 The effects of compressor speed on the relative exergy loss of system components

由图4可知, 随着压缩机转速的增加, 气冷器和压缩机的相对㶲损增大, 膨胀阀和蒸发器的相对㶲损减小。压缩机转速较低时, 膨胀阀的相对㶲损最大, 压缩机的相对㶲损最小, 当压缩机转速为3 000 r/min时, 膨胀阀、气冷器、蒸发器和压缩机的相对㶲损分别是37.24%、23.4%、20.37%和18.97%。随着压缩机转速的增加, 气冷器的相对㶲损最大, 蒸发器的相对㶲损最小, 当压缩机转速为8 000 r/min时, 气冷器、压缩机、膨胀阀和蒸发器的相对㶲损分别为29.71%、27.76%、26.11%和16.42%。表3展现了不同的压缩机转速下各部件的平均相对㶲损。由表可知, 膨胀阀的平均相对㶲损最大, 平均占比31.10%, 其次是气冷器和压缩机, 平均占比分别为26.93%和23.47%, 蒸发器的相对㶲损最小, 平均占比18.49%。

表3 不同的压缩机转速下系统各部件平均相对㶲损 Table 3 Average relative exergy loss of system components at different compressor speeds

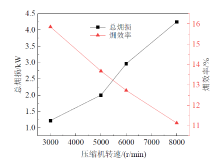
图5展示了压缩机转速对系统总㶲损和㶲效率的影响。由图可知, 随着压缩机转速增加, 系统的总㶲损逐渐大幅度增大, 㶲效率逐渐减小。当压缩机转速从3 000 r/min增加至8 000 r/min时, 系统总㶲损从1.22 kW增大至4.25 kW, 㶲效率从15.85%减小至11.13%。这是由于随着压缩机转速的增加, 压缩机的排气温度逐渐升高, 压缩机和气冷器内由于与环境之间的换热造成的不可逆损失逐渐增加, 㶲损逐渐增加, 其相对㶲损逐渐增大, 而膨胀阀和蒸发器的温度更接近环境温度, 压缩机转速变化导致的温度变化相对于压缩机和气冷器较小, 因此膨胀阀和蒸发器的㶲损增加幅度相对较小, 其相对㶲损逐渐减小。由于压缩机转速的提升, 系统的制冷剂流量大幅增加, 系统总㶲损增加。同时, 系统获得的冷量㶲增加, 但压缩机功耗提升更显著, 因此系统㶲效率随压缩机转速增加而降低。

图5 压缩机转速对㶲效率和总㶲损的影响Fig. 5 The effects of compressor speed on the exergy efficiency and total exergy loss of system

3.2 气体冷却器进风风速的影响

在表2所列的工况2下, 气冷器进风风速对系统各部件㶲损失和相对㶲损的影响如图6、图7所示。由图6可知, 随着气冷器进风风速的增加, 蒸发器㶲损失值逐渐增大, 气冷器、压缩机、膨胀阀㶲损失值逐渐减小, 但变化幅度均减小, 逐渐趋于平稳。当气冷器进风风速由1 m/s增加至5 m/s时, 气冷器、压缩机与膨胀阀的㶲损失值分别由0.443、0.381、0.708 kW降至0.286、0.232、0.455 kW, 分别减小了35.44%、39.11%、35.73%, 蒸发器㶲损失值由0.181 kW增至0.249 kW, 增加了37.57%。

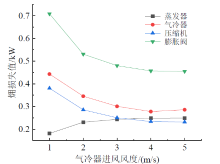图6 气冷器进风风速对系统各部件㶲损值的影响Fig. 6 The effects of air inlet speed of gas cooler on the exergy loss of system components

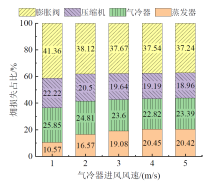图7 气冷器进风风速对系统各部件相对㶲损的影响Fig. 7 The effects of air inlet speed of gas cooler on the relative exergy loss of system components

由图7可知, 随着气冷器进风风速的增加, 气冷器、压缩机和膨胀阀的相对㶲损先减小, 后趋于平稳, 蒸发器的相对㶲损先增加后趋于平稳。气冷器进风风速较低时, 膨胀阀的相对㶲损最大, 蒸发器的相对㶲损最小, 当气冷器进风风速为1 m/s时, 膨胀阀、气冷器、压缩机和蒸发器的相对㶲损分别为41.36%、25.86%、22.22%和10.57%。随着气冷器进风风速的增加, 膨胀阀的相对㶲损仍最大, 压缩机的相对㶲损最小。当气冷器进风风速为5 m/s时, 膨胀阀、气冷器、蒸发器和压缩机的相对㶲损分别为37.24%、23.39%、20.42%和18.96%。表4展现了不同的气冷器进风风速下各部件的平均相对㶲损, 由表可知, 膨胀阀的相对㶲损最大, 平均占比38.39%, 其次是气冷器和压缩机, 平均占比分别为24.10%和20.10%, 蒸发器的相对㶲损最小, 平均占比17.42%。

表4 不同的气冷器进风风速下系统各部件平均相对㶲损 Table 4 Average relative exergy loss of system components at different air inlet speed of gas cooler

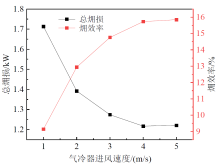
图8展示了气冷器进风风速对系统总㶲损和㶲效率的影响。由图可知, 随着气冷器进风风速的增加, 总㶲损先快速减小后趋于平缓, 㶲效率先快速增大后趋于平缓。当气冷器风速从1 m/s增加到5 m/s时, 总㶲损从1.71 kW减小到1.22 kW, 㶲效率从9.14%增加到15.85%。这是由于随着气冷器进风风速的增加, 气冷器对处于超临界状态的CO2制冷剂冷却效果越显著, 气冷器出口的制冷剂温度降低, 为维持系统设定的5 ℃过热度, 膨胀阀开度增大, 压缩机的压比减小。压缩机和膨胀阀内制冷剂的平均温度减小, 与环境换热造成的不可逆损失减小, 相应的㶲损减小。气冷器内的制冷剂平均温度减小, 而气冷器外的空气温度略有降低, 但由于空气温度降幅较小且与环境温度相差较小, 综合两者因素, 气冷器由于与环境换热的不可逆损失减小, 相应㶲损减小。蒸发器内制冷剂温度减小, 增大了与空气的换热温差, 因此蒸发器与空气换热的不可逆损失增大, 相应㶲损增大。虽然蒸发器的㶲损随着气冷器出风温度的升高而增大, 但压缩机、膨胀阀和气冷器的㶲损减小, 在各部件的综合影响下, 系统的总㶲损减小。随着蒸发器空气温度的降低, 系统获得的㶲增加, 系统付出的㶲即压缩机功耗减小, 系统的㶲效率增大。由于气冷器体积的确定, 其最大换热能力受限, 当接近最大换热能力时, 继续增加气冷器进风风速不能使气冷器内的制冷剂降温, 系统的运行状态变化较小, 因此当气冷器进风风速继续增加时, 总㶲损和㶲效率变化逐渐缓慢, 直至相对平缓。

图8 气冷器进风风速对总㶲损和㶲效率的影响Fig. 8 The effects of air inlet speed of gas cooler on the exergy efficiency and total exergy loss of system

3.3 气体冷却器进风温度的影响

在表2所列的工况3下, 气冷器进风温度对系统各部件㶲损失和相对㶲损的影响如图9、图10所示。由图9可知, 随着气冷器进风温度的升高, 蒸发器㶲损失值逐渐减小, 膨胀阀、气冷器、压缩机㶲损失值逐渐增大, 其中, 膨胀阀㶲损失值受气冷器进风温度变化影响最大, 气冷器㶲损失值受影响最小。当气冷器进风温度由30 ℃升高至46 ℃时, 膨胀阀㶲损失值由0.369 kW增至0.676 kW, 增加了83.20%, 气冷器、压缩机㶲损失值分别由0.281、0.199 kW增至0.295、0.301 kW, 分别增加了4.98%、51.26%, 蒸发器㶲损失值由0.276 kW降至0.187 kW, 减小了32.24%。

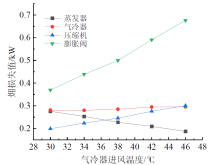图9 气冷器进风温度对系统各部件㶲损值的影响Fig. 9 The effects of air inlet temperature of gas cooler on the exergy loss of system components

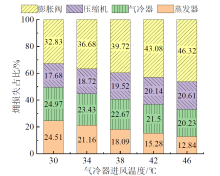图10 气冷器进风温度对系统各部件相对㶲损的影响Fig. 10 The effects of air inlet temperature of gas cooler on the relative exergy loss of system components

由图10可知, 随着气冷器进风温度的升高, 膨胀阀和压缩机的相对㶲损增加, 气冷器和蒸发器的相对㶲损减小。气冷器进风温度较低时, 膨胀阀的相对㶲损最大, 压缩机的相对㶲损最小, 当气冷器进风温度为30 ℃时, 膨胀阀、气冷器、蒸发器和压缩机的相对㶲损分别为33.16%、25.22%、24.75%和17.86%。随着气冷器进风温度的升高, 膨胀阀的相对㶲损仍最大, 蒸发器的相对㶲损较小, 当气冷器进风温度为46 ℃时, 膨胀阀、压缩机、气冷器和蒸发器的相对㶲损分别为46.32%、20.61%、20.23%和12.84%。表5展现了不同的气冷器进风温度下各部件的平均相对㶲损, 由表可知, 膨胀阀的相对㶲损最大, 平均占比39.73%, 其次是气冷器和压缩机, 平均占比分别为22.56%和19.33%, 蒸发器的相对㶲损最小, 平均占比18.38%。

表5 不同的气冷器进风温度下系统各部件平均相对㶲损 Table 5 Average relative exergy loss of system components at different air inlet temperature of gas cooler

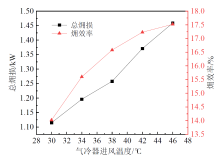
图11展示了气冷器进风温度对系统总㶲损和㶲效率的影响。由图可知, 随着气冷器进风温度的升高, 总㶲损和㶲效率逐渐增大。当气冷器进风温度从30 ℃升高至46 ℃时, 总㶲损从1.12 kW增加到1.46 kW, 㶲效率从14.02%增加到17.52%。这是由于随着气冷器进风温度的升高, 气冷器出口的制冷剂温度也随之升高, 为维持系统设定的5 ℃过热度, 膨胀阀开度减小, 压缩机的压比增大。压缩机和膨胀阀内制冷剂的平均温度升高, 与环境温度温差增大, 不可逆损失增加, 由于膨胀阀开度减小, 膨胀阀内的损耗更大, 相应的㶲损增幅更显著。气冷器内制冷剂的平均温度升高, 但是由于环境温度（即气冷器进风温度）同时升高, 因此气冷器内制冷剂和外侧空气的平均温度与环境温度的温差上升较低, 㶲损增加较小, 相较于膨胀阀和压缩机的增长, 其相对㶲损减小。蒸发器内制冷剂与外侧空气的平均温度升高, 换热温差减小, 不可逆损失减小, 相应的㶲损降低。在各部件的综合影响下, 系统的总㶲损随气冷器进风温度的升高而增大。随着气冷器进风温度的升高, 系统的制冷性能减弱, 压缩机耗功增加, 但气冷器温度的升高意味着环境温度也升高, 环境温度的升高会导致系统获得的冷量㶲增加, 综合影响下, 系统㶲效率随着气冷器进风温度的升高而增大。

图11 气冷器进风温度对总㶲损和㶲效率的影响Fig. 11 The effects of air inlet temperature of gas cooler on the exergy efficiency and total exergy loss of system

3.4 蒸发器进风量的影响

在表2所列的工况4下, 蒸发器进风量对系统各部件㶲损失和相对㶲损的影响如图12、图13所示。由图12可知, 随着蒸发器进风量的增加, 膨胀阀㶲损失值逐渐增大, 气冷器与压缩机㶲损失值逐渐减小, 蒸发器㶲损失值先减小后增大。随着蒸发器进风量由300 m3/h增加至700 m3/h, 膨胀阀㶲损失值由0.424 kW增至0.455 kW, 增加了7.31%; 气冷器与压缩机㶲损失值由0.313、0.276 kW降至0.286、0.232 kW, 分别减小了8.63%、15.94%; 蒸发器㶲损失值先由0.254 kW降至0.230 kW, 减小了9.45%, 之后又增加至0.249 kW, 增加了8.26%。

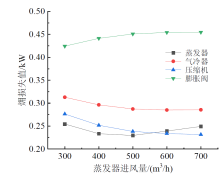图12 蒸发器进风量对系统各部件㶲损值的影响Fig. 12 The effects of air inlet volume of evaporator on the exergy loss of system components

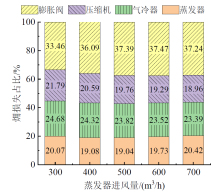图13 蒸发器进风量对系统各部件相对㶲损的影响Fig. 13 The effects of air inlet volume of evaporator on the relative exergy loss of system components

由图13可知, 随着蒸发器进风量的增加, 膨胀阀的相对㶲损先增大后趋于平稳, 气冷器和压缩机的相对㶲损减小, 蒸发器的相对㶲损先减小后增大。蒸发器进风量较低时, 膨胀阀的相对㶲损最大, 蒸发器的相对㶲损最小, 当蒸发器进风量为300 m3/h时, 膨胀阀、气冷器、压缩机和蒸发器的相对㶲损分别为33.46%、24.68%、21.79%和20.07%。随着蒸发器进风量的增加, 膨胀阀的相对㶲损仍最大, 压缩机的相对㶲损最小, 当蒸发器进风量为700 m3/h时, 膨胀阀、气冷器、蒸发器和压缩机的相对㶲损分别为37.24%、23.39%、20.42%和18.96%。表6展示了不同的蒸发器进风量下各部件的平均相对㶲损失, 由表可知, 膨胀阀的相对㶲损最大, 平均占比36.33%, 其次是气冷器和压缩机, 平均占比分别为23.93%和20.08%, 蒸发器的相对㶲损最小, 平均占比19.67%。

表6 不同的蒸发器进风量下系统各部件平均相对㶲损 Table 6 Average relative exergy loss of system components at different air inlet volume of evaporator

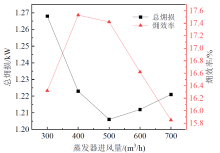
图14展现了蒸发器进风量对总㶲损和㶲效率的影响。由图可知, 随着蒸发器进风量的增加, 总㶲损先减小后增大, 㶲效率先增大后减小。当蒸发器进风量从300 m3/h增加至700 m3/h时, 总㶲损先从1.268 kW减小到1.206 kW, 再增加到1.221 kW, 㶲效率先从16.32%增加到17.53%, 再减小到15.85%。这是由于随着蒸发器进风量的增加, 蒸发器的换热能力逐渐增强, 为维持系统设定的5 ℃过热度, 膨胀阀开度增大, 压比减小, 蒸发温度上升, 制冷剂流量增加。压缩机、气冷器内制冷剂的平均温度降低, 换热造成的不可逆损失减小, 相应的㶲损减小。虽然膨胀阀进出口制冷剂的温度逐渐接近环境温度, 但是膨胀阀由换热温差造成的不可逆损失影响较小, 由于制冷剂质量流量的增加, 膨胀阀的㶲损在综合影响下增加。蒸发器内制冷剂的温度逐渐升高, 外侧的空气温度逐渐升高, 换热温差逐渐缩小, 蒸发器的㶲损减小, 但蒸发器的换热能力受限, 蒸发器进风量增加到一定量时, 蒸发温度变化较小, 外侧空气的出风温度逐渐升高, 制冷剂与空气的温差增大, 且制冷剂的质量流量增加, 综合影响下蒸发器的㶲损当进风量到达一定值后逐渐增大。由于蒸发器的换热能力受限, 系统的总㶲损整体呈现先减小后增大。蒸发器外侧的空气温度逐渐升高, 单位质量下系统获得的冷量㶲减少, 压缩机压比减小, 压缩机耗功减小, 综合影响下, 蒸发器的㶲效率随着蒸发器进风温度的升高呈现先增加后减小。

图14 蒸发器进风量对总㶲损和㶲效率的影响Fig. 14 The effects of air inlet volume of evaporator on the exergy efficiency and total exergy loss of system

3.5 蒸发器进风温度的影响

在表2所列的工况5下, 蒸发器进风温度对系统各部件㶲损失和相对㶲损的影响如图15、图16所示。由图15可知, 随着蒸发器进风温度的升高, 膨胀阀与蒸发器㶲损失值逐渐增大, 气冷器与压缩机㶲损失值逐渐减小。当蒸发器进风温度由20 ℃升高至28 ℃时, 膨胀阀与蒸发器㶲损失值分别由0.439、0.230 kW增至0.465、0.257 kW, 分别增加了5.92%、11.74%, 气冷器与压缩机㶲损失值由0.305、0.257 kW降至0.271、0.215 kW, 分别减小了11.15%、16.34%。

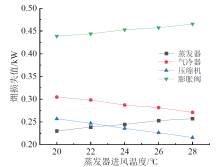图15 蒸发器进风温度对系统各部件㶲损值的影响Fig. 15 The effects of air inlet temperature of evaporator on the exergy loss of system components

由图16可知, 随着蒸发器进风温度的升高, 膨胀阀和蒸发器的相对㶲损增加, 压缩机和气冷器的相对㶲损减少。蒸发器进风温度较低时, 膨胀阀的相对㶲损最大, 蒸发器的相对㶲损最小。当蒸发器进风温度为20 ℃时, 膨胀阀、气冷器、压缩机和蒸发器的相对㶲损分别为35.67%、24.77%、20.88%和18.69%。随着蒸发器进风温度的升高, 膨胀阀的相对㶲损仍最大, 压缩机的相对㶲损最小。当蒸发器进风温度为28 ℃时, 膨胀阀、气冷器、蒸发器和压缩机的相对㶲损分别为38.50%、22.41%、21.27%和17.82%。表7展现了不同的蒸发器进风温度下各部件的平均相对㶲损。由表可知, 膨胀阀的相对㶲损最大, 平均占比37.00%, 其次是气冷器和蒸发器, 平均占比分别为23.62%和20.04%, 压缩机的相对㶲损最小, 平均占比19.34%。

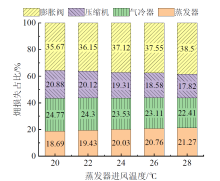图16 蒸发器进风温度对系统各部件相对㶲损的影响Fig. 16 The effects of air inlet temperature of evaporator on the relative exergy loss of system components

表7 不同的蒸发器进风温度下系统各部件平均相对㶲损 Table 7 Average relative exergy loss of system components at different air inlet temperature of evaporator

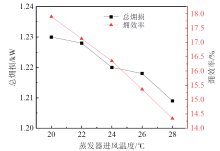
图17展示了蒸发器进风温度对总㶲损和㶲效率的影响。由图可知, 随着蒸发器进风温度的升高, 㶲损和㶲效率逐渐降低。当蒸发器进风温度从20 ℃升高至28 ℃时, 总㶲损从1.230 kW减小到1.209 kW, 㶲效率从17.90%减小到14.34%。这是由于随着蒸发器进风温度的升高, 进风温度与制冷剂温差增大, 换热器换热能力增加, 为维持系统设定的5 ℃过热度, 膨胀阀开度增大, 压比减小。压缩机和气冷器内制冷剂的平均温度降低, 不可逆损失减小, 相应的㶲损降低。由于压比的减小, 压缩机的容积效率增加, 系统的制冷剂质量流量增加, 虽然膨胀阀内的制冷剂平均温度略有降低, 但在制冷剂流量增加的影响下膨胀阀的总㶲损微弱增加。蒸发器内制冷剂与外侧空气温度均升高, 换热温差增大, 同时在制冷剂流量增加的影响下㶲损略微增加。在各部件的综合影响下, 系统总㶲损随着蒸发器进风温度的升高而略微减小。由于蒸发器进风温度的升高, 虽然压缩机耗功减小, 但系统获得的冷量㶲降低, 导致㶲效率随蒸发器出风温度升高而降低。

图17 蒸发器进风温度对总㶲损和㶲效率的影响Fig. 17 The effects of air inlet temperature of evaporator on the exergy efficiency and total exergy loss of system

4 总结

构建了车用跨临界CO2空调系统, 通过仿真对系统的变工况性能进行了研究, 在仿真数据基础上对系统进行了㶲分析, 得到以下结论：

（1）随着压缩机转速的提升, 系统各部件㶲损失均增大, 压缩机和气体冷却器的相对㶲损增加, 膨胀阀和蒸发器的相对㶲损减小, 系统的总㶲损增大, 㶲效率降低。膨胀阀平均㶲损占比最大, 平均相对㶲损为31.10%, 蒸发器平均相对㶲损最小, 为18.49%。

（2）随着气体冷却器进风风速的增加, 气冷器、压缩机、膨胀阀㶲损失和相对㶲损减小, 蒸发器㶲损失和相对㶲损增大, 系统的总㶲损减小, 㶲效率升高, 增加和降低趋势逐渐缓慢。膨胀阀平均㶲损占比最大, 平均相对㶲损为38.39%, 蒸发器平均相对㶲损最小, 为17.42%。

（3）随着气体冷却器进风温度的升高, 气冷器、压缩机、膨胀阀㶲损失增大, 蒸发器㶲损失减小, 膨胀阀和压缩机的相对㶲损增加, 气体冷却器和蒸发器的相对㶲损减小, 系统的总㶲损增大, 㶲效率升高。膨胀阀平均㶲损占比最大, 平均相对㶲损为39.79%, 蒸发器平均相对㶲损最小, 为18.42%。

（4）随着蒸发器进风量的增加, 气冷器和压缩机㶲损失和相对㶲损减小, 膨胀阀㶲损失和相对㶲损增大, 蒸发器㶲损失和相对㶲损先减后增, 系统总㶲损先减后增, 㶲效率先增后减。膨胀阀平均㶲损占比最大, 平均相对㶲损为36.37%, 蒸发器平均相对㶲损最小, 为19.67%。

（5）随着蒸发器进风温度的升高, 气冷器和压缩机㶲损失和相对㶲损减小, 膨胀阀和蒸发器㶲损失和相对㶲损增大, 系统总㶲损减小, 㶲效率降低。膨胀阀平均㶲损占比最大, 平均相对㶲损为37.05%, 压缩机平均相对㶲损最小, 为19.34%。

综上, 在车用跨临界CO2空调系统中, 膨胀阀和气体冷却器内的㶲损占比最大, 同时, 气体冷却器进风风速和进风温度对㶲损影响较大。因此在优化车用跨临界CO2空调系统时需要重点关注节流过程和气体冷却器内的冷却过程, 搭建跨临界CO2空调系统时需要重点关注气体冷却器进风风速和进风温度与气体冷却器大小的匹配。

参考文献
[1] 刘援, 孙丹妮, 张建君, 等. 中国履行《蒙特利尔议定书(基加利修正案)》减排三氟甲烷的对策分析[J]. 气候变化研究进展, 2018, 14(4): 423-428. DOI: 10.12006/j.issn.1673-1719.2017.237. [本文引用:1]
[2] 李慧, 曹祥, 张春路. 二氧化碳热泵技术的发展及应用案例分析[J]. 化工进展, 2016, 35(S2): 421-426. DOI: 10.16085/j.issn.1000-6613.2016.s2.074. [本文引用:1]
[3] LORENTZEN G, PETTERSEN J. A new, efficient and environmentally benign system for car air conditioning[J]. International journal of refrigeration, 1993, 16: 4-12. DOI: 10.1016/0140-7007(93)90014-Y. [本文引用:1]
[4] 刘洪胜, 陈江平, 陈芝久. CO2充注量对跨临界轿车空调系统性能的影响[J]. 化工学报, 2005, 56(8): 1426-1432. DOI: 10.3321/j.issn:0438-1157.2005.08.009. [本文引用:1]
[5] KAUF F. Determination of the optimum high pressure for transcritical CO2-refrigeration cycles[J]. International journal of thermal sciences, 1999, 38(4): 325-330. DOI: 10.1016/S1290-0729(99)80098-2. [本文引用:1]
[6] LIAO S M, ZHAO T S, JAKOBSEN A. A correlation of optimal heat rejection pressures in transcritical carbon dioxide cycles[J]. Applied thermal engineering, 2000, 20(9): 831-841. DOI: 10.1016/S1359-4311(99)00070-8. [本文引用:1]
[7] KIM S C, WON J P, KIM M S. Effects of operating parameters on the performance of a CO2 air conditioning system for vehicles[J]. Applied thermal engineering, 2009, 29(11/12): 2408-2416. DOI: 10.1016/j.applthermaleng.2008.12.017. [本文引用:1]
[8] CHO H, BAEK C, PARK C, et al. Performance evaluation of a two-stage CO2 cycle with gas injection in the cooling mode operation[J]. International journal of refrigeration, 2009, 32(1): 40-46. DOI: 10.1016/j.ijrefrig.2008.07.008. [本文引用:1]
[9] BAEK C, LEE E, KANG H, et al. Experimental study on the heating performance of a CO2 heat pump with gas injection[C]//International Refrigeration and Air Conditioning Conference at Purdue. West Lafayette: Purdue University, 2008. [本文引用:1]
[10] 董丽玮, 李敏霞, 姚良, 等. 带引射器的跨临界CO2机械过冷热泵系统性能分析[J]. 化工进展, 2021, 40(10): 5431-5440. DOI: 10.16085/j.issn.1000-6613.2020-2077. [本文引用:1]
[11] 方健珉, 王静, 孙西峰, 等. 回热器对电动汽车跨临界CO2制冷系统影响的实验研究[J]. 西安交通大学学报, 2020, 54(6): 155-160. DOI: 10.7652/xjtuxb202006020. [本文引用:1]
[12] YANG J L, MA Y T, LI M X, et al. Exergy analysis of transcritical carbon dioxide refrigeration cycle with an expand er[J]. Energy, 2005, 30(7): 1162-1175. DOI: 10.1016/j.energy.2004.08.007. [本文引用:1]
[13] ÖZGÜR A E, KABUL A, KIZILKAN O. Exergy analysis of refrigeration systems using an alternative refrigerant (hfo-1234yf) to R-134a[J]. International journal of low-carbon technologies, 2014, 9(1): 56-62. DOI: 10.1093/ijlct/cts054. [本文引用:1]
[14] YANG M H, YEH R H. Performance and exergy destruction analyses of optimal subcooling for vapor-compression refrigeration systems[J]. International journal of heat and mass transfer, 2015, 87: 1-10. DOI: 10.1016/j.ijheatmasstransfer.2015.03.085. [本文引用:1]
[15] 马进伟, 方浩, 陈茜茜, 等. 基于焓-熵-㶲平衡的无盖板PV/T系统热力学分析与优化[J]. 化工进展, 2022, 41(4): 1840-1847. DOI: 10.16085/j.issn.1000-6613.2021-2135. [本文引用:1]
[16] 赵维维, 娄德仓, 钟世林. 基于㶲分析和代偿损失的热管理系统性能评价方法[J]. 航空动力学报, 2023, 38(12): 2829-2836. doi: 10.13224/j.cnki.jasp.20220121. [本文引用:1]