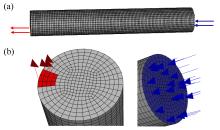
气化装置主要由气化炉、蓄热系统和供风系统组成。气化炉形制为上吸式, 炉体呈圆柱形, 内径150 mm, 高约1 000 mm, 包括上料斗、进料螺旋、燃气出口、宝塔式炉排、灰室。上料斗位于炉体顶端, 燃气出口位于炉体顶部侧面, 炉排与灰室位于炉体底部; 蓄热系统包括位于气化炉下部的环形蓄热腔室, 腔室内填充有蓄热材料; 供风系统包括鼓风机和位于环形蓄热腔室内的供风盘管; 其余已配备的辅助构件包括输运气体所需的管路, 监测气化炉内以及管路关键节点处温度与压力的热电偶、压力计, 风机、流量计、小型燃烧室、电箱和控制终端等, 气化装置示意图如图1所示。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
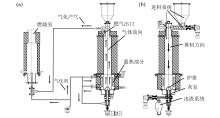	图1 气化装置示意图：（a）整体系统; （b）气化炉Fig. 1 Gasification device schematic diagram: (a) whole system; (b) gasifier

本装置应用了蓄热技术^{[18, 19]}, 在炉下方化学反应剧烈、温度较高的氧化还原区外部增设蓄热腔室, 内部填充蓄热材料（实验中使用直径约2 mm的钢球）使其与炉内气化过程进行能量传递, 吸收、储存与释放炉内产生的热量, 稳定炉内温度场, 进而维持反应过程稳定。工作原理如图2所示。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
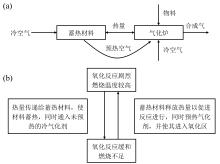	图2 气化装置工作原理：（a）工作流程; （b）蓄热部分反馈-控温环节Fig. 2 Working principle of gasification device: (a) flow chart; (b) thermal energy storage feedback-temperature control link

对于该气化装置的实验和已进行过的部分数值模拟工作, 前期研究^[17]已阐明, 并通过模拟结果与实验的对比证明了本研究中所用模拟方法的准确性, 其内容在本研究中不再赘述。本文采用的固废原料为木质生物质, 由林业固废压缩成型制成, 呈圆柱形, 直径5 ~ 7 mm, 高为直径的3 ~ 5倍, 其工业分析与元素分析结果见表2。

表2

Table 2

表2(Table 2)

表2 木质生物质固废原料工业分析和元素分析 Table 2 Industry analysis and elemental analysis of woody biomass solid waste raw material 工业分析/% 元素分析/% 挥发分 固定碳 灰分 C H N 82.951 16.677 0.372 48.00 6.35 0.02

表2 木质生物质固废原料工业分析和元素分析 Table 2 Industry analysis and elemental analysis of woody biomass solid waste raw material

原料灰分极少, 模拟中将不考虑灰分的影响; 元素分析测得原料中N含量仅为0.02%, 可忽略不计, 即认为原料中只含C、H、O（其中O含量为45.65%）三种元素。则本固废原料完全燃烧的原料质量与所需气化剂（空气）质量比为1∶ 6.34。本装置设计原料处理量为3 ~ 5 kg/h, 本研究取3.6 kg/h, 即0.001 kg/s, 相应的过量空气系数对应的气化剂流率依此算出。

1.2.1 网格划分

采用CFD-DDPM模型将气化炉几何模型简化为一圆柱形筒体, 采用结构化网格对气化炉进行网格划分, 在保留气化炉重要几何特征的同时规避了网格质量差的风险。

炉体上部设置一扇形合成气压力出口, 炉底为气化剂质量流量入口, 炉膛底部（0.126 m）至约0.4 m处外壁设置为蓄热壁面。为验证研究中所用网格在数值计算中的准确性和精确性, 进行了网格数量敏感性分析。将气化炉分为三个不同尺寸的网格（小尺寸网格数为360 000, 中等尺寸网格数为155 100, 大尺寸网格数为32 967）, 计算流速随炉膛高度的变化, 结果如图3所示, 三套网格的流速几乎保持不变, 证明了网格划分的合理性。本研究选择尺寸最大的网格进行计算。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
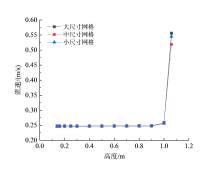	图3 不同尺寸网格中流体流度随装置高度的变化Fig. 3 The variation of fluid velocity with device height in meshes of different sizes

网格模型总计32 967个网格, 35 608个节点, 101 340个网格面, 最小网格质量0.84, 远大于网格质量的最小阈值（0.3左右）, 可以很好地完成气化过程的计算。气化炉网格划分如图4所示, 网格尺寸在5 ~ 15 mm左右。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 气化炉网格划分：（a）整体划分; （b）局部划分Fig. 4 Gasifier meshing: (a) global meshing; (b) local meshing

1.2.2 连续相数学模型

（1）质量守恒

$\frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{{\vec{u}}}_{\text{f}}} \right)={{S}_{\text{m}}}$ (1)

式中：t为时间, s; ε _f为流体体积分数; ρ _f为流体密度, kg/m³; ${{\vec{u}}_{\text{f}}}$为流体速度, m/s; S_m为流体与颗粒间的质量传递速率, kg∙ m^-3∙ s^-1。

（2）动量守恒

$\begin{align} & \frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{{\vec{u}}}_{\text{f}}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{{\vec{u}}}_{\text{f}}}{{{\vec{u}}}_{\text{f}}} \right)=-{{\varepsilon }_{\text{f}}}\nabla p+ \\ & \nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{{\bar{\bar{\tau }}}}_{\text{f}}} \right)+{{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}\vec{g}+{{K}_{\text{sf}}}\left( {{{\vec{u}}}_{\text{s}}}-{{{\vec{u}}}_{\text{f}}} \right)+{{S}_{\text{mom}}} \\ \end{align}$ (2)

式中：p为流体压力, Pa; ${{\bar{\bar{\tau }}}_{\text{f}}}$为偏应力张量, kg∙ m^-1∙ s^-2; $\vec{g}$为重力加速度, m/s²; K_sf为流体与颗粒间相互作用的曳力系数, kg∙ m^-3∙ s^-1; ${{\vec{u}}_{\text{s}}}$为颗粒速度, m/s; S_mom为包含颗粒与流体相互传递质量造成的动量改变, kg∙ m^-2∙ s^-2。

（3）能量方程

$\begin{align} & \frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{H}_{\text{f}}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{{\vec{u}}}_{\text{f}}}{{H}_{\text{f}}} \right)={{\varepsilon }_{\text{f}}}\frac{\partial p}{\partial t}+{{{\bar{\bar{\tau }}}}_{\text{f}}}:\nabla {{{\vec{u}}}_{\text{f}}}+ \\ & \ \ \ \ \ \ \nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{\lambda }_{\text{f}}}\nabla {{T}_{\text{f}}} \right)+\underset{i=1}{\overset{m}{\mathop \sum }}\, \left[ {{h}_{\text{f, }}}_{i}{{A}_{\text{s}}}\left( {{T}_{\text{s}}}-{{T}_{\text{f}}} \right) \right]+{{S}_{\text{en}}} \\ \end{align}$ (3)

式中：H_f为流体的焓, kJ/kg; λ _f为导热系数, kJ∙ m^-2∙ K^-1∙ s^-1; h_{f, i}为颗粒与流体组分i间的传热系数, kJ∙ m^-5∙ K^-1∙ s^-1; A_s为颗粒表面积, m²; T_s为颗粒温度, K; T_f为流体温度, K; S_en为流体中由于化学反应及辐射产生或吸收的热量, kJ∙ m^-3∙ s^-1。

（4）组分输运方程：

$\begin{align} & \frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{Y}_{j}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{{\vec{u}}}_{\text{f}}}{{Y}_{j}} \right)= \\ & \nabla \cdot \left( {{\varepsilon }_{\text{f}}}{{\rho }_{\text{f}}}{{D}_{\text{eff, f}}}\nabla {{Y}_{j}} \right)+{{S}_{j\text{, hom}}}+{{S}_{j\text{, hete}}} \\ \end{align}$ (4)

式中：Y_j为流体中组分j的质量分数; D_{eff, f}为质量扩散系数; S_{j, hom}为组分j均相反应的组分质量交换, kg∙ m^-3∙ s^-1; S_{j, hete}为组分j异相反应的组分质量交换, kg∙ m^-3∙ s^-1。

1.2.3 离散相数学模型

动量守恒

${{m}_{\text{s}}}\frac{\text{d}{{{\vec{u}}}_{\text{s}}}}{\text{d}t}={{m}_{\text{s}}}\vec{g}+{{V}_{\text{s}}}{{K}_{\text{fs}}}\left( {{{\vec{u}}}_{\text{f}}}-{{{\vec{u}}}_{\text{s}}} \right)+{{\vec{F}}_{\text{s}}}+{{\vec{F}}_{\text{other}}}$ (5)

式中：${{m}_{\text{s}}}$为颗粒质量, kg; ${{V}_{\text{s}}}$为颗粒体积, m³; K_fs为颗粒与流体间相互作用的曳力系数; ${{m}_{\text{s}}}\vec{g}$表示重力; ${{V}_{\text{s}}}{{K}_{\text{fs}}}\left( {{{\vec{u}}}_{\text{f}}}-{{{\vec{u}}}_{\text{s}}} \right)$表示流体与颗粒间相互作用力; ${{\vec{F}}_{\text{s}}}$为颗粒间作用力; ${{\vec{F}}_{\text{other}}}$为剩余形式的粒子力, 如压力梯度力、虚拟质量力等。本研究中颗粒基本处于静止状态, 颗粒密度远大于流体密度, 颗粒额外受力${{\vec{F}}_{\text{other}}}$影响极小, 因此不考虑这些力的影响^[20]。

对于流体与颗粒间相互作用力, 如何确定曳力系数是计算流固两相动量耦合的关键。本文采用非均相的、基于介尺度结构的能量最小多尺度（energy minimization multi-scale, EMMS）曳力模型, 相比于均相曳力模型, EMMS曳力模型能够更好地分辨网格尺度内的曳力变化^{[21, 22]}, 相关模型及参数由文献[21, 23-24]给出。

关于离散相间相互作用力${{\vec{F}}_{\text{s}}}$的计算, DDPM模型有两种处理方式, 一种是采用基于颗粒动理学理论（kinetic theory of granular flow, KTGF）通过模型化离散相间作用力来封闭方程组^[25], 一种是耦合DEM软球模型, 直接求取单个颗粒上的作用力进行计算^[26]。本研究采用耦合DEM的方法。关于颗粒碰撞过程中所需的参数及其取值, 由参考文献[26, 27, 28]给出。

颗粒升温后, 经历水分蒸发、挥发分热解及焦炭还原的过程。当颗粒温度高于373.15 K时, 含有水分的颗粒水分蒸发。颗粒热解过程可表示为：

$生物质(干燥)\to a{{\text{H}}_{\text{2}}}+b\text{C}{{\text{H}}_{\text{4}}}+c\text{C}{{\text{O}}_{\text{2}}}+d\text{CO}+\text{C}\left( \text{s} \right)$ (6)

文献[29]总结了数种常见的生物质类型固废的挥发分组分质量分数, 其材料特性与本研究所用原料类似, 均为木质生物质, 同时热解温度相近, 因此本研究对其结果取平均值处理, 作为挥发分中各组分质量分数选取依据, 见表3。忽略焦油的影响, 将焦油等液态产物计入CH₄中。

表3

Table 3

表3(Table 3)

表3 挥发分各组分质量分数 Table 3 Mass fraction of volatile species 组分 质量分数/% H2 2.225 CH4 18.850 CO 37.650 CO2 41.275

表3 挥发分各组分质量分数 Table 3 Mass fraction of volatile species

热解反应速率采用单步反应速率^[26]进行计算：

$-\frac{\text{d}{{m}_{\text{s}}}}{\text{d}t}={{k}_{\text{pyro}}}\left[ {{m}_{\text{s}}}-\left( 1-{{f}_{\text{v, 0}}} \right)\left( 1-{{f}_{\text{w, 0}}} \right){{m}_{\text{s, 0}}} \right]$ (7)

式中：f_{v, 0}为挥发分质量分数; f_{w, 0}为水分质量分数; m_{s, 0}为颗粒初始质量, kg; k_pyro为热解反应速率常数。

动力学速率可表示为^[26]：

${{k}_{\text{pyro}}}={{A}_{\text{pyro}}}\exp \left( -\frac{{{E}_{\text{pyro}}}}{R{{T}_{\text{p}}}} \right)$ (8)

式中：A_pyro和E_pyro分别为热解反应的指前因子与活化能, 取值参考文献[27], 其中A_pyro = 5 × 10⁶ s^-1, E_pyro = 1.2 × 10⁸ J/kmol。

热解后焦炭异相表面反应速率为^{[26, 28, 30]}：

$\frac{\partial {{m}_{\text{c}\left( \text{s} \right)}}}{\partial t}=-{{A}_{\text{s}}}{{Y}_{j\text{, f}}}\frac{R{{\rho }_{\text{f}}}{{T}_{\text{f}}}}{{{M}_{j}}}\frac{{{k}_{j}}{{k}_{\text{diff, }}}_{j}}{{{k}_{j}}+{{k}_{\text{diff, }}}_{j}}$ (9)

焦炭异相表面反应速率由与颗粒表面气体扩散速率相关的扩散反应速率和与温度相关的动力学反应速率两个反应速率控制。

其中, 扩散反应速率为^[28]：

${{k}_{\text{diff, }j}}={{C}_{j}}\frac{{{\left[ 0.5\left( {{T}_{\text{s}}}+{{T}_{\text{f}}} \right) \right]}^{0.75}}}{{{d}_{\text{s}}}}$ (10)

式中：C_j为扩散速率常数, 取值为5 × 10^-12 s∙ K^-0.75[26]; d_s为颗粒直径, m。

动力学反应速率为：

${{k}_{j}}={{A}_{\text{hete}}}{{T}_{\text{s}}}\text{exp}\left( -\frac{{{E}_{\text{hete}}}}{R{{T}_{\text{s}}}} \right)$ (11)

异相反应考虑焦炭与CO₂、H₂O的反应, 其指前因子A_hete与活化能E_hete取值如表4所示。

表4

Table 4

表4(Table 4)

表4 异相反应参数[27] Table 4 Heterogeneous phase reaction parameters[27] 反应 Ahete/(s∙ m-1∙ K-1) Ehete/(J/kmol) C(s) + H2 → H2 + CO 45.6 4.37 × 107 C(s) + CO2 → 2CO 8.3 4.37 × 107

表4 异相反应参数[27] Table 4 Heterogeneous phase reaction parameters[27]

均相反应考虑三个还原反应及三个氧化反应, 有限速率模型参数^{[27, 31]}如表5所示。

表5

Table 5

表5(Table 5)

表5 均相反应参数 Table 5 Homogeneous phase reaction parameters 反应 Ahomo/(kmol/m3) Ehomo/(J/kmol) CO + H2O → CO2+ H2 2.780 × 103 1.260 × 107 CO2 + H2 → CO + H2O 9.590 × 104 4.660 × 107 CH4 + H2O → 3H2+ CO 3.000 × 108 1.260 × 108 CO + 0.5O2 → CO2 3.987 × 1014 1.674 × 108 CH4 + 2O2 → CO2 + 2H2O 1.585 × 1013 2.025 × 108 H2 + 0.5O2 → H2O 1.995 × 1012 1.092 × 108

表5 均相反应参数 Table 5 Homogeneous phase reaction parameters

前期研究^[17]中, 颗粒初始温度、组分等物理量一致, 未在炉内形成随气化程度不同而产生的不同颗粒物性分布梯度, 致使模拟结果较为片面, 对整体气化状态的还原存在不足。因此在本研究中, 考虑上吸式固定床气化反应的特性, 于前处理阶段设计五种颗粒, 使其存在含水率、温度梯度及挥发分含量的差异, 颗粒相关设置见表6, 颗粒呈现出下部温度较高, 气化进程逐渐加深的状态。颗粒设计为直径3 mm的球形颗粒, 按前处理中颗粒设置的顺序依次落下, 最终呈固定床形态填充于炉中, 如图5所示。

表6

Table 6

表6(Table 6)

表6 颗粒基础参数设置 Table 6 Particles basic parameter settings 颗粒种类 含水率/% 挥发分含量/% 初始温度/K 释放时刻/s 固废1 0 30.0 773.15 0.2 固废2 0 60.0 625.15 0.4 固废3 0 83.0 500.15 0.6 固废4 10 74.7 400.15 0.8 焦炭 0 0.0 1 173.15 0.0

表6 颗粒基础参数设置 Table 6 Particles basic parameter settings

图5

Fig. 5

	Figure Option ViewDownloadNew Window
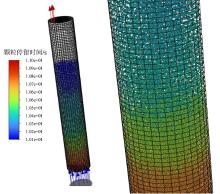	图5 颗粒呈固定床形式填充炉内（右侧为局部放大图）Fig. 5 Particles in the form of a fixed bed filling the furnace (localized enlargement on the right)

待颗粒全部落入炉内后, 通入1 100 K高温氮气10 s加热颗粒, 促进颗粒水分蒸发和热解, 使不同颗粒的温度梯度减小。随后通入温度为1 173.15 K的空气作为气化剂, 计算时间为50 s。根据前期研究^[17]的经验, 气化剂流率过大会导致炉内物理场失稳, 出现不合理的温度、组分分布, 同时降低气化产气中可燃气体的质量分数, 因此本研究取较低气化剂流率, 过量空气系数α 分别取0.1、0.2、0.3、0.4。本研究所用CFD软件为Fluent, 其余相关的数值模拟模型及参数取值见表7。

表7

Table 7

表7(Table 7)

表7 模型及参数设置 Table 7 Model and parameter settings 相关模型及参数 模型选择及参数取值 湍流模型 Realizable k-ε 辐射模型 Discrete Ordinates (DO) 蓄热部分壁面温度/K 1 000 流体时间步长/s 2 × 10-4 离散相时间步长/s 2 × 10-5

表7 模型及参数设置 Table 7 Model and parameter settings

由图6可知, 过量空气系数越高, 炉内流速及其局部波动越大, 流速增长主要集中于颗粒床层区域。由图7可知, 不同时刻炉内流速在分布和数值上变化不大, 气化过程较为稳定。不同工况下流速分布相似, 均迅速增大至炉高约0.4 m处后趋于平稳。随着过量空气系数的增加, 流速分别稳定在约0.8、1.1、1.3、1.6 m/s附近; 而在炉高0.7 ~ 0.8 m处, 流速则略微增大（增幅约0.1 m/s）, 这是由于此处颗粒含水, 干燥过程增加了流体动量。

图6

Fig. 6

	Figure Option ViewDownloadNew Window
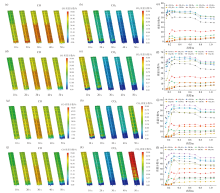
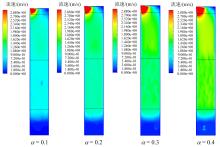	图6 45 s时不同过量空气系数下流速分布云图Fig. 6 Cloud diagrams of velocity distribution under different excess air coefficients at 45 s

图7

Fig. 7

	Figure Option ViewDownloadNew Window
	图7 不同时刻流速分布Fig. 7 Velocity distribution at different times

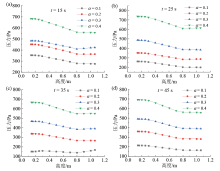
由图8、图9可知, 气体压力沿炉膛轴线方向自下而上缓慢下降, 颗粒床层区域气体压力的持续下降为合成气向炉顶部燃气出口的流动提供了动力, 而颗粒床层上部的气体压力较为平稳。不同过量空气系数下, 气体压力的绝对数值不同, 但压降的幅度相近。从气化剂进入炉底到气体流出颗粒床层的过程均产生了约50 ~ 75 Pa的压降, 说明结构与高度相同的颗粒床层是影响气体压降的主要原因。不同工况下压力分布场相似, 气体压力在较长的模拟时间内并无明显变化, 压力场稳定, 这与前期模拟所得结果^[17]有较大差别。压力与速度的计算结果均在较长模拟时间内保持稳定, 表明本研究前处理设置有效, 气化过程呈现出准稳态特征。

图8

Fig. 8

	Figure Option ViewDownloadNew Window
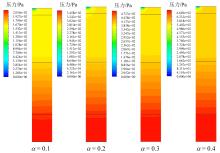	图8 45 s时不同过量空气系数下气体压力分布云图Fig. 8 Cloud diagrams of gas pressure distribution under different excess air coefficients at 45 s

图9

Fig. 9

	Figure Option ViewDownloadNew Window
	图9 不同时刻气体压力分布Fig. 9 Gas pressure distribution at different times

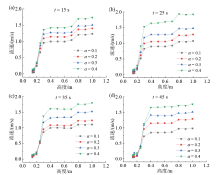
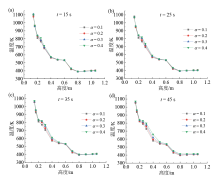
由图10可知, 不同工况下炉内温度场分布相似, 上吸式固定床气化具有的干燥-热解-还原氧化分区较为清晰, 从炉顶到炉底逐渐升高的温度分布基本形成, 炉温在350 ~ 1 100 K之间, 未出现不合理的极高温或极低温区域。

图10

Fig. 10

	Figure Option ViewDownloadNew Window
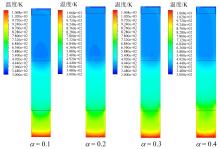	图10 45 s时不同过量空气系数下温度分布云图Fig. 10 Cloud diagrams of temperature distribution under different excess air coefficients at 45 s

由图11可知, 炉温随着时间推移无明显变化, 各工况温度曲线几乎重叠, 呈现出较为统一的拐点特征。第一个拐点在约0.2 m处, 此处为底部炭层与固废颗粒交界处, 温度自炉底至此处迅速从约1 100 K下降至800 K左右, 这是由于在炭层中大量焦炭与CO₂发生还原反应吸热, 而当气体进入固废颗粒区域后, 焦炭数量减少, 还原反应减弱, 导致后续温度变化趋于平缓。第二个拐点在0.4 m处, 此区间（0.2 ~ 0.4 m）大致为炭层顶部至蓄热部分与炉中上部交界, 温度从800 K下降至约550 K, 蓄热壁面温度较高, 固废颗粒热解基本在此处进行, 颗粒吸收大量热量, 温度下降较快, 而相比于下层还原反应区温度梯度小。第三个拐点位于0.6 m处, 在0.4 ~ 0.6 m间温度下降不足50 K, 此段炉壁面为绝热壁面, 不具备高温的边界条件, 导致颗粒热解反应速率慢, 吸热速率减小。经过0.6 m处后温度梯度增大, 在0.6 ~ 0.8 m范围内, 温度由520 K下降至约400 K。第四个拐点在0.8 m处, 此时气体已脱离颗粒区域, 温度曲线平缓, 无明显变化。四个拐点将炉体划分为五个不同的区间：氧化还原区（≤ 0.2 m）-快速热解区（0.2 ~ 0.4 m）-慢速热解区（0.4 ~ 0.6 m）-干燥区（0.6 ~ 0.8 m）-燃气流出区（≥ 0.8 m）。

图11

Fig. 11

	Figure Option ViewDownloadNew Window
	图11 不同时刻温度分布Fig. 11 Temperature distribution at different times

综合而言, 温度场的模拟结果符合理想情况下上吸式固定床固废气化应有的温度分布区间, 较先前研究^[17]更为合理。温度与流速、压力的模拟结果随时间变化均较小, 实现了炉内准稳态气化, 证明了本研究优化后的前处理设置成功复现了气化过程稳定持续产气的阶段。

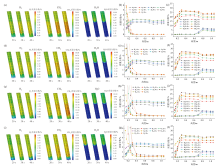
由图12可知, 炉内CO质量分数随着时间的推移表现出先升高后降低的趋势, 而CO₂则相反。在相同时刻, CO的质量分数沿炉膛高度先升高后降低。炉底部炭层中, 焦炭与CO₂反应生成大量CO, 同时炭层上部固废颗粒热解也生成大量CO, 因此CO质量分数持续增大, 并在约0.3 m处达到峰值, 随后保持稳定（约40% ~ 60%）, 成为炉中下部的主要气体产物。在0.7 m以上, CO质量分数明显下降（降幅约10% ~ 15%）, 最终稳定在35% ~ 55%之间。下降的主要原因是水分的蒸发导致大量H₂O生成, 同时CO与H₂O反应生成CO₂。在不同的过量空气系数下, CO₂质量分数呈现出随时间变化的相似规律, 在计算前20 s时, CO₂自炉底快速生成, 在约0.225 m处达到峰值（10% ~ 25%）, 随后小幅下降并保持稳定, 并有小幅增长（≤ 5%）, 且过量空气系数越大, 增长幅度越小。而在后20 s, CO₂质量分数快速增长至0.4 m处后保持平稳且小幅增长。当α = 0.1时, 炉中上部CO₂平均质量分数基本在10%以下, 到α = 0.4时, CO₂质量分数已增长至15% ~ 30%。总体而言, CO质量分数大于CO₂, 分别维持在35% ~ 65%及5% ~ 30%之间。在相同时刻, 随着过量空气系数的增加, CO整体含量降低而CO₂含量升高。

图12

Fig. 12

	Figure Option ViewDownloadNew Window
	图12 不同过量空气系数下CO、CO2在不同时刻的质量分数分布：（a ~ c）α = 0.1; （d ~ f）α = 0.2; （g ~ i）α = 0.3; （j ~ l）α = 0.4Fig. 12 The mass fraction distribution of CO and CO2 at different times under different excess air coefficients: (a-c) α = 0.1; (d-f) α = 0.2; (g-i) α = 0.3; (j-l) α = 0.4

由图13可知, 不同过量空气系数下H₂的质量分数分布类似, 在 ≤ 0.3 m时快速增大, 之后趋于平稳, 各工况均维持在2% ~ 3%之间, 不同时刻变化幅度不超过1%, 在 ≥ 0.8 m小幅增长（≤ 0.3%）。O₂基本只存在于炉底部, 0.4 m后几乎完全被消耗（≤ 1%）, 过量空气系数越大, O₂扩散的区域越大。CH₄在 ≤ 0.3 m时快速增大, 在0.7 m处小幅降低, 总体维持在18% ~ 25%之间。由于水分蒸发, H₂O从0.6 m处开始大量产生, 直至0.8 m处到达峰值（5% ~ 7.5%）后逐渐下降。随着时间推移, 相同位置处H₂O质量分数逐渐下降, 过量空气系数越大, H₂O质量分数降幅越大。自α = 0.1 ~ 0.4, H₂O质量分数降幅在3% ~ 7%左右。

图13

Fig. 13

	Figure Option ViewDownloadNew Window
	图13 不同过量空气系数下H2、CH4、H2O、O2在不同时刻的质量分数分布：（a ~ c）α = 0.1; （d ~ f）α = 0.2; （g ~ i）α = 0.3; （j ~ l）α = 0.4Fig. 13 The mass fraction distribution of H2, CH4, H2O, and O2 at different times under different excess air coefficients: (a-c) α = 0.1; (d-f) α = 0.2; (g-i) α = 0.3; (j-l) α = 0.4

总体而言, 炉中下部（0.3 ~ 0.7 m）各气体组分质量分布变化较小, 而在0.7 ~ 0.8 m区间由于水分蒸发, 除H₂O外其余气体质量分数均小幅减少, 尤其是可燃气体H₂、CH₄、CO均展现相似的分布特征。炉底部存在大量焦炭和O₂, 可燃气体进行氧化反应生成H₂O及CO₂, 同时焦炭与H₂O和CO₂发生还原反应, 氧化反应与还原反应区域集中于炉底部, 因此在本装置中氧化区与还原区界限并不明显。各组分质量分数变化最大的区域为炉底至快速热解区（≤ 0.4 m）, 固废颗粒大量析出挥发分, 而在离开蓄热壁面后, 颗粒缺少热量, 热解过程减缓。对于本装置而言, 温度及组分分布与蓄热部分关系紧密。

由图14可知, 随着时间的推移, 产气CO质量分数先增后降, 在低过量空气系数（α ≤ 0.3）条件下维持在40% ~ 50%之间, 较为稳定, 而在α ≤ 0.4时则在计算后期明显下降; H₂质量分数在2% ~ 3%之间; CH₄质量分数在15% ~ 23%之间; CO₂质量分数先降后升, 浮动较大, 最高达30%, 最低降至10%以下; N₂质量分数在低气化剂流率下较为稳定, 约为10% ~ 15%, 在高气化剂流率下有小幅下降, 从20%缓慢降至10%, 证明高气化剂流率促进了颗粒的热解; O₂基本被耗尽, 表明氧化反应效果明显, 燃气出口几乎不含O₂; H₂O小幅下降, 最终在5%以下。

图14

Fig. 14

	Figure Option ViewDownloadNew Window
	图14 不同时刻出口气体质量分数Fig. 14 Mass fraction of outlet gas at different times

总体而言, 过量空气系数越大, 各气体组分波动越大, 这与前期模拟结果^[17]相同。当α ≤ 0.2时, 不同过量空气系数下燃气出口组分质量分数随时间变化曲线类似; 而α = 0.3时, 在模拟时间的最后20 s, CO₂质量分数明显增大, 而在α = 0.4时, CO、CH₄在模拟后15 s均出现小幅减少, CO₂出现大幅增大, 这表明在该工况下消耗的可燃气体质量较高, 出现对气化反应不利的情况。

取50 s内不同过量空气系数下出口处H₂质量分数的平均值与所有工况的总平均值, 与实验结果进行比较, 结果如图15所示。所有数据的误差均小于10%, 其中总平均值误差小于5%, 表明模拟结果与实验结果较为符合, 验证了模拟结果的准确性。

图15

Fig. 15

	Figure Option ViewDownloadNew Window
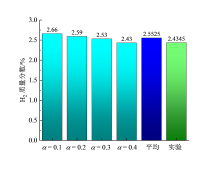	图15 不同过量空气系数下出口处H2质量分数及平均值与实验平均值对比Fig. 15 Comparison of H2 mass fraction and average value at the outlet with experimental average under different excess air coefficients

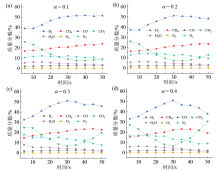
取出口气体组分质量分数的平均值进行分析, 如图16所示。在较长时间的气化过程中, 发现不同过量空气系数下H₂、CH₄质量分数相差不多, 分别维持在2.5% ~ 3%、19% ~ 20%之间。相较于前期研究^[17]的模拟结果, 两者的质量分数均有一定程度的提升。H₂含量的提升归因于焦炭与H₂O的还原反应以及炉上部CO与H₂O反应的共同作用, H₂为热值最高的可燃气体, 其提升对提高燃气质量有利; CH₄主要来源于颗粒热解, 其含量的升高表明热解程度的加深, 对整体反应有利。CO的质量分数随着过量空气系数的增加而小幅减小, 平均降幅在1%左右, 总体维持在43% ~ 47.5%之间; 与此同时, CO₂质量分数有小幅提升, 总体维持在13% ~ 17%, 大部分CO₂被还原, CO/CO₂转化效果良好, 表明该炉设计较为成功。总体而言, 过量空气系数的增加对合成气气体组分影响不大, 表明在本研究选取的低过量空气系数区间, 气化剂流率调整的灵活性较高, 可在较低的过量空气系数区间进行产气流量调节而无需承担气体热值过低的代价。

图16

Fig. 16

	Figure Option ViewDownloadNew Window
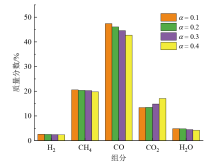	图16 不同过量空气系数出口处各气体质量分数平均值Fig. 16 The average mass fraction of each gas at the outlet with different excess air coefficients

在气化过程中, 气化产气的H₂的质量分数和CO/CO₂质量分数之比十分重要。H₂的质量分数越高, CO/CO₂比值越大, 气体热值越高, 产气热值高对气化结果有利, 特别是H₂, 其单位质量具有较高的热值, 氧化反应产物是H₂O, 是清洁、性能优越的可燃气体。对大量上吸式固定床气化的研究结果进行了比较, 详见表8。对每个研究中气化产生的H₂、CO和CO₂的质量分数进行平均, 并以三种气体的质量分数之和作为基准, 得出H₂、CO和CO₂的相对质量分数。

表8

Table 8

表8(Table 8)

表8 当前工作与以往研究中气体组分质量分数的比较 Table 8 Comparison of gas species mass fractions between current work and previous research 文献 固废类型 气化剂种类 气体组分质量分数/% H2 CO CO2 本文 生物质 空气 3.92 72.50 23.58 [15] 煤 空气-水蒸气 2.27 68.60 29.13 [32] 生物质 空气 1.46 51.64 46.90 [14] 生物质 空气 1.31 68.80 29.89 [8] 生物质 空气 1.36 51.00 47.64 [1] 生物质 空气; 空气-水蒸气 3.00 63.47 33.53 [33] 生物质 水蒸气 5.90 11.30 82.80

表8 当前工作与以往研究中气体组分质量分数的比较 Table 8 Comparison of gas species mass fractions between current work and previous research

通过对比表8, 当原料均为生物质类固废且气化剂为空气时, 本研究所用的气化装置产气的H₂质量分数比其他研究高约1.3 ~ 3倍, 具有显著优势。这种新设计的气化装置有利于增加H₂产量, 这可能是由于本装置实现了对炉内温度及气化过程的稳定控制, 促进了H₂O的重整。在最后两项研究中, H₂的质量分数很高, 归因于气化剂中存在水蒸气, 而本研究的装置在不使用水蒸气作为气化剂的情况下实现了高H₂产率。该装置中气体的CO/CO₂质量分数之比也有大幅提升, 同样也有利于提升燃气热值。综上, 燃气热值的提升证明了装置设计的优越性。