引用本文
刘猛, 沈宇豪, 颜应文, 田泽民. 典型丙醚二级加氧产物的氢转移裂解反应理论研究[J]. 新能源进展, 2024,12(5): 580-587
LIU Meng, SHEN Yuhao, YAN Yingwen, TIAN Zemin. Theoretical Study on the H-Transfer Reaction Combining with Dissociation for the Typical Intermediates of Secondary O2-Addition for Propyl Ethers [J]. ADV NEW RENEWABLE EN, 2024,12(5): 580-587.  
Doi: 10.3969/j.issn.2095-560X.2024.05.009
Permissions
Copyright©2024, 《新能源进展》编辑部
版权所有 © 《新能源进展》编辑部
典型丙醚二级加氧产物的氢转移裂解反应理论研究
刘猛, 沈宇豪, 颜应文, 田泽民†
南京航空航天大学 能源与动力学院,南京 210016
†通信作者：田泽民,E-mail：tzm@nuaa.edu.cn

作者简介：刘 猛（1998-）,男,硕士研究生,主要从事替代燃料低温氧化研究。田泽民（1991-）,男,博士,副教授,硕士生导师,主要从事化学反应动力学研究。

收稿日期: 2024-01-04 修订日期:: 2024-03-25
基金项目: 江苏省自然科学青年基金项目（BK20200451）
摘要

低温燃烧是一种有前景的高效清洁燃烧技术。其关键问题之一在于可靠地构建燃料低温氧化化学动力学机理。丙醚作为一种可再生清洁燃料,在低温燃烧方面有较高应用潜力,然而,其关键低温氧化反应的研究却十分缺乏。基于量子化学和过渡态理论,考虑物种的多重构象效应,计算三种典型的正丙醚/异丙醚二级过氧化物OOQOOH经过氢转移-裂解生成氢过氧化物醛酮类物质和OH基的反应势能面、热力学数据和反应速率常数。结果表明,多重构象效应对物种的焓、熵、定压比热容及速率常数有明显影响,计算时不可忽略。获得的热力学数据和反应速率常数可用于完善丙醚燃料低温氧化机理。

关键词: 二级加氧反应; 势能面; 丙醚; 速率常数; 量子化学
中图分类号:TK421 文献标识码:A 文章编号:2095-560X（2024）05-0580-08
Theoretical Study on the H-Transfer Reaction Combining with Dissociation for the Typical Intermediates of Secondary O2-Addition for Propyl Ethers
LIU Meng, SHEN Yuhao, YAN Yingwen, TIAN Zemin†
School of Energy and Power, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
Abstract

Low-temperature combustion is a promising efficient and clean combustion technology. One of the key problems is constructing reliable chemical kinetic mechanism of low-temperature oxidation for practical fuels. Propyl ethers, a renewable clean fuel, have great potential in low-temperature combustion. However, there is a shortage of its low-temperature chemical kinetics studies. This work investigated three typical reactions of secondary O2-addition intermediates related to n-/iso-propyl ethers, denoting as OOQOOH, forming ketohydroperoxides plus OH, based on quantum chemistry and transition state theory. Potential energy surfaces, thermodynamic data and rate constants were obtained and refined using the multi-structure method. It was shown that the multi-structure torsional anharmonicity exerts notable influences on thermodynamic data and rate constants, which can be further used to improve the low-temperature chemical mechanism of propyl ethers.

Key words: secondary O2-addition reaction; potential energy surface; propyl ether; rate constant; quantum chemistry
0 引言

发展高效清洁的燃烧技术一直是动力装置燃烧部件的主旨之一。近年来, 我国提出了“ 碳达峰” 目标, 使清洁燃烧技术的需求更为迫切[1]。传统的汽油、柴油等化石燃料的主要成分是链烷烃, 燃烧不完全易生成碳烟、未燃碳氢等污染物[2]。

以醚类为代表的含氧燃料可由生物质转化而来, 具有可再生的优势, 其分子中含有氧原子, 相比烷烃含碳更少, 更容易实现完全燃烧; 产生的CO2更少, 是一类清洁燃料[3]。

实现清洁燃烧的另一途径是发展新型燃烧技术。关于均质压燃着火（homogeneous charge compression ignition, HCCI）、反应控制压燃着火（reactivity controlled compression ignition, RCCI）等燃烧技术的大量研究表明, 在内燃机中采用此类燃烧技术能够同时实现燃烧效率的提高和污染物排放的降低[4, 5, 6]。然而这些技术的瓶颈之一在于, 必须实现燃料低温着火过程的精准控制, 因此必须掌握燃料的低温氧化特性。醚类燃料低温氧化性能高, 适合此类低温燃烧技术。因此, 研究醚类燃料的低温氧化特性具有明确的潜在应用价值[7]。

二甲醚是最简单醚类燃料, 其相关研究丰富[8, 9, 10]。但作为小分子气态燃料, 其体积能量密度低, 不易与液态燃油混用。以丙醚为代表的C6醚类燃料一定程度上能够克服这些问题, 是醚类燃料的研究焦点。

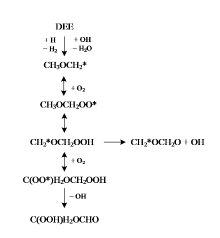
SERINYEL等[11, 12]利用射流搅拌反应器研究了正丙醚的低温裂解过程, 提出了详细的低温氧化机理。UYUMAZ等[13]测试了HCCI模式下, 添加不同比例二异丙醚对气缸压力、燃烧持续时间、制动扭矩等参数的影响, 结果表明, 添加异丙醚后火焰向爆震区和部分燃烧区扩展。图1以乙醚（diethyl ether, DEE）为例展示了醚类燃料复杂的低温氧化路径, 以往低温氧化研究[11, 12, 14, 15, 16, 17]主要集中在一级加氧的低温反应路径。二级加氧过程, 即一级加氧反应生成的过氧化物（QOOH）进一步加氧生成过氧基过氧化物（OOQOOH）反应路径的相关研究十分稀少。

图1 乙醚低温氧化的主要路径Fig. 1 Main paths of low temperature oxidation for DEE

丙醚有正丙醚和异丙醚两种同分异构体, 本文针对两者反应生成的代表性OOQOOH自由基, 开展其最重要的反应路径— — 氢转移裂解生成氢过氧化物醛酮类物质（ketohydroperoxide, KHP）和OH的基元反应特征研究, 获得相应反应的速率常数。

1 计算方法

采用量子化学方法对基元反应的反应物、过渡态及产物的分子结构进行优化, 并计算其单点能。然后基于过渡态理论计算其速率常数。

另一方面, 分子内CH2、OOH基团的空间排布使每个分子具有多种空间异构构象, 与之相关的基团内转动具有振-转非谐耦合特性。以往研究表明这种效应对物种热力学参数和基元反应速率常数有显著影响[18, 19, 20]。为了考虑这种影响机制, 需要在分子的内转动自由度内计算所有空间构象。具体的计算步骤如下：①获得能量计算可靠的密度泛函方法; ②搜索优化所有物种的空间异构结构; ③优化和计算所有结构的分子能量和振动频率; ④考虑多结构效应, 计算热力学数据; ⑤基于过渡态理论, 计算基元反应速率常数。

1.1 量子化学方法

使用一种密度泛函[M062-X/6-311++g(d, p)]方法, 对反应物、过渡态和产物的能量最低的构象进行结构优化, 并利用CCSD(T)-F12a/jun-cc-pVTZ[21, 22]方法计算电子能。同时, 针对每个物种, 使用5种密度泛函方法：M05-2X[23]、TPSSH、BHHLYP、WB97X-D[24]、B3LYP; 并搭配选用6个不同基组：MG3S、def2-TZVPP、cc-pVTZ、aug-cc-pVTZ、jul-cc-pVTZ、jun-cc-pVTZ[25], 即使用30种不同的计算方法, 优化其分子结构并计算单点能。比较这些方法获得的单点能与基准方法获得的单点能差异的平均值, 选择偏差最小的方法作为全局计算方法。各方法对比结果如表1所示, 通过比较特定反应36个数据的平均误差, 发现BHHLYP/cc-pVDZ与CCSD(T)-F12a/jun-cc-pVTZ的差值仅为1.55 kJ/mol, 要明显低于其他计算方法的结果, 因此选用BHHLYP/cc-pVDZ和基组作为最优的结构优化和频率计算方法。获得的单点能作为基准, 用于筛选能够较好计算物种能量的密度泛函方法。

表1 相对于CCSD(T)-F12a/jun-cc-pVTZ的平均误差 Table 1 Average error relative to CCSD(T)-F12a/jun-cc-pVTZ

分子空间构象的计算方法是：独立旋转每个除甲基外的C— C键二面角获得大量的初猜分子结构, 然后利用选定的密度泛函方法, 即BHHLYP/cc-pVDZ方法, 对所有结构进行优化, 删去收敛到相同构象的计算结果, 即获得了优化计算后的所有空间异构的分子结构。同时, 也获得了所有分子结构的单点能和振动频率。至此, 完成①②③步。

所涉及的构象搜索使用Mstor[26, 27]程序完成, 所有的量子化学计算均使用ORCA软件[28, 29]。

1.2 热力学数据及速率常数计算

基于统计热力学相关理论, 物种的热力学参数（熵、焓、定压比热容）可以通过分子的配分函数获得。分子的配分函数是分子的平动配分函数、振-转配分函数及电子能配分函数的乘积。考虑多结构效应的分子配分函数计算方法如式（1）所示：

${{Q}^{\text{MS-T}}}=\underset{j=1}{\overset{N}{\mathop{\sum }}}\, {{Q}_{\text{rot}, j}}\exp \left( -\frac{{{U}_{j}}}{{{k}_{\text{B}}}T} \right)Q_{j}^{\text{QH}}\underset{\tau =1}{\overset{t}{\mathop{\prod }}}\, {{f}_{j, \tau }}$ (1)

其中：T为温度; ${{k}_{\text{B}}}$为波尔兹曼常数; $\tau $为耦合扭转的势函数; ${{Q}^{\text{MS-T}}}$为分子振-转配分函数; j为该分子的一个空间构象; ${{Q}_{\text{rot}, j}}$为该分子构象的转动配分函数; ${{U}_{j}}$为该构象相对于最稳定构象的能量差值; $Q_{j}^{\text{QH}}$为该构象的振动简谐配分函数; ${{f}_{j, \tau }}$为该结构振-转耦合效应的影响。使用该方法获得的热力学数据用MS-T表示; 若不考虑振-转耦合效应, 即${{f}_{j, \tau }}$取1, 则记为MS-LH; 若仅考虑分子能量最低的构象的配分函数, 获得的结果记为SS-HO。

基元反应的速率常数基于过渡态理论计算, 并利用多结构效应进行校正。速率常数${{k}^{\text{MS-T/TST}}}$由基于过渡态理论获得的速率常数${{k}^{\text{TST}}}$与多重构象校正因子$F_{\text{act}}^{\text{MS-T}}$乘积获得：

${{k}^{\text{MS-T/TST}}}=F_{\text{act}}^{\text{MS-T}}{{k}^{\text{TST}}}$(2)

式（3）给出过渡态理论计算速率常数的方法：

${{k}^{\text{TST}}}=\kappa \frac{{{k}_{\text{B}}}T}{h}\frac{{{Q}^{\ddagger }}}{{{Q}_{\text{R}}}}\exp \left[ -{{E}_{0}}/\left( {{k}_{\text{B}}}T \right) \right]$ (3)

式中：${{Q}^{\ddagger }}$和${{Q}_{\text{R}}}$分别对应最低能量构象的过渡态、反应物的配分函数; E0为过渡态和反应物两者之间的能量差; $\kappa $为隧道效应因子。

$F_{\text{act}}^{\text{MS-T}}$作为反应的多重构象校正因子, 可由式（4）得到：

$F_{\text{act}}^{\text{MS-T}}=F_{\text{TS}}^{\text{MS-T}}/F_{\text{R}}^{\text{MS-T}}$ (4)

式中：$F_{\text{R}}^{\text{MS-T}}$、$F_{\text{TS}}^{\text{MS-T}}$分别为反应物和过渡态的多重构象影响因子, 其计算方法如下：

$F_{X}^{\text{MS-T}}=\frac{Q_{\text{rovib}}^{\text{MS-T}}\ \ \ (X)}{Q_{\text{rovib}}^{\text{SS-QH}}\ \ \ (X)}$ (5)

其含义是考虑多重构象效应获得的配分函数与最低能量结构获得的配分函数的比值。

2 结果和讨论
2.1 分子构象

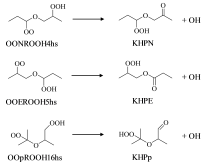
图2为所计算的三个基元反应。OOpROH16hs是异丙醚的低温氧化产物, 而OONROOH4hs、OOEROOH5hs是正丙醚的脱羟基产物。

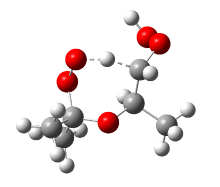
图2 三个OOQOOH物种及其反应产物Fig. 2 Three OOQOOH species and their reaction products

结果表明, 三个基元反应的反应物OOpROOH16hs、OONROOH4hs、OOEROOH5hs的构象数目分别为194、256、281, 其相应过渡态TS-p16、TS-N4、TS-E5的构象数目分别为6、21、25, 如图3所示。由于反应物分子结构的C— C键转动自由度大, 因此构象数目众多, 不同构象间的电子能差异最高可达到41.8 kJ/mol。而过渡态的构象数目大幅减少, 主要原因是过渡态结构中的氧原子与被吸取的氢原子形成了环状络合键显著限制了化学键的空间转动（图4）。

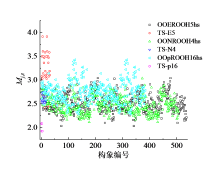
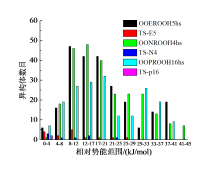图3 物种在每个相对势能范围内空间异构体的数量布居Fig. 3 The population of distinguishable isomers of different species within each relative potential energy range

图4 典型过渡态分子结构Fig. 4 Molecular structure of typical transition state

从本质上来讲, 分子不同构象对应基团绕C— C键转动一周产生的1个或数个极小值, 也称为物种的局域周期。而由于C— C键之间的耦合作用, 不同C— C键转动产生的极小值有相干性。因此, 在如图5所示的反应物和过渡态的局域周期数是介于2 ~ 3之间的非整数。

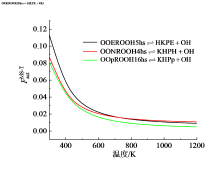
图5 物种的局域周期性Mj, τ Fig. 5 Local periodicity Mj, τ of species

2.2 热力学参数

根据分子的平动、振-转运动配分函数及其电子能配分函数获得其总配分函数, 从而可以直接计算该分子的热力学参数, 如熵、定压比热容、焓。图6给出了所涉及物种在298 ~ 1 200 K温度范围内的配分函数。图中可见, MS-LH和MS-T方法获得的配分函数相差较小, 前者比后者高24% ~ 36%。而根据SS-HO方法获得的配分函数远低于MS-T方法的结果, 并且随着温度升高, 差异越大。基于不同方法下的配分函数, 获得了各物种的热力学参数, 如表2所示。在室温下, 基于MS-T方法获得的焓值比MS-LH方法高0.63 kJ/mol, 当温度升高到1 200 K后, 前者比后者高0.35 kJ/mol, 总体而言, 差异变化较小。对比而言, SS-HO方法获得的焓值比MS-T方法获得的结果低9.2 ~ 18.4 kJ/mol, 具有显著差别。熵和定压比热容的对比结果与焓值的结果一致。由此可见, 对于长链物种, 采用MS-T方法考虑振-转非谐效应是十分必要的。

图6 利用不同方法计算获得的配分函数Fig. 6 The partition functions obtained using different methods

表2 使用不同方法计算得到的标准熵、定压比热容和相对焓 Table 2 Standard entropy, heat capacity, and relative enthalpy calculated using different methods
2.3 反应速率常数

图7为利用BHHLYP/cc-pVDZ方法获得的三个基元反应的势能面。其中, 用能量最低的构象代表每个物种, 势能面的能垒计算考虑了零点能效应。图中可见, 异丙醚相关的OOQOOH生成KHP + OH反应的能垒显著低于正丙醚相关物种的反应能垒。另一方面, 计算结果也表明三个基元反应是显著的放热反应, 也反映了该类反应对燃料低温氧化的促进作用。

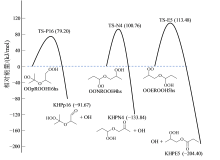图7 在BHHLYP/cc-pVDZ级别下最低能量构象的势能面Fig. 7 The potential energy surface of the lowest energy conformation at the BHHLYP/cc-pVDZ level

基元反应的速率常数受到反应物和过渡态结构配分函数的共同影响。表征其综合效应的参数$F_{\text{act}}^{\text{MS-T}}$随温度的变化结果如图8所示。图中可见, 对于三个反应, 该参数在300 K下取值约为0.1, 而后迅速降低到600 K时的0.02, 此后对温度不再敏感。其含义在于, 相比于常规的仅考虑反应物和过渡态的最低能量构象并将振动视为谐振的计算方法, 采用更为客观准确的多结构非谐耦合（MS-T）方法获得的结果低90% ~ 98%, 显示了多结构非谐效应对基元反应速率常数的突出影响。因此, 对于低温加氧反应及其他长链碳氢燃料的基元反应速率常数研究中, 参与反应的各物种的空间构象及非谐效应不可忽略。

图8 反应的多结构扭转非谐性因子Fig. 8 Multistructural torsional anharmonicity factor of reactions

图9显示了在298 ~ 1 200 K温度范围内, 三个反应$\text{OOEROOH5hs}\rightleftharpoons \text{HKPE}+\text{OH}$（简称RE5）、$\text{OONROOH4hs}\rightleftharpoons \text{KHPH}+\text{OH}$(简称RN4)、$\text{OOpROOH16hs}\rightleftharpoons \text{KHPp}+\text{OH}$（简称RP16）的速率常数。虚线是不考虑多重构象效应, 仅利用最低能量结构计算获得的速率常数; 实线是考虑多重构象效应后获得的结果。尽管经计算表明, 本文采用的密度泛函方法获得的能垒与高精度耦合簇方法相比, 偏差小于1.7 kJ/mol, 为了谨慎评估计算不确定度, 将各种影响因素折算成能垒偏差考虑, 可认为能垒的计算不确定度为 ± 4.2 kJ/mol。以速率常数最大的反应RP16为例, 获得了该反应速率常数随温度变化的不确定度：在300 K下为3.8倍, 而温度升高到1 200 K时降到1.5倍。因此, 可认为本文中速率常数的计算结果不确定度不超过4倍。

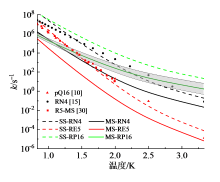图9 本文计算的高压极限速率常数（实线使用MS-CVT/SCT方法计算, 简称MS; 虚线使用SS-CVT/SCT方法计算, 简称SS）与文献中相似反应的速率常数的比较（pQ16取自文献[10], 与RP16比较; RN4取自文献[15], 与RN4比较; R5-MS取自文献[30], 与反应RE5比较）Fig. 9 High pressure limit rate constants in this work (solid lines: MS-CVT/SCT method, denoted as MS; dash lines: SS-CVT/SCT method, as SS) compared with literature data (pQ16 from ref. [10] versus RP16; RN4 from ref. [15] versus RN4; R5-MS from ref. [30] versus RE5)

对比图9中虚线与实线发现, 前者是后者的10 ~ 100倍, 随着温度升高, 二者的差异越大, 表明考虑多结构效应后, 基元反应速率常数变为原来的1% ~ 0.1%。这是由于考虑多重构象效应后, 反应物和过渡态的配分函数增大, 而反应物构象多, 受到更大的影响, 增幅更为显著。

另一方面, 通过对比不同OOQOOH反应的速率常数可以发现三者的差异。反应RP16的速率常数最高, RN4的次之, RN5的最低, 这主要取决于它们的能垒高低：反应RP16的能垒比反应RN4的能垒约低20.9 kJ/mol, 而反应RN4的能垒比反应RN5的能垒低12.5 kJ/mol。另外随着温度升高至超过1 000 K, 反应RN4的速率有反超反应RP16的趋势, 这是由于反应RN4的配分函数对速率常数的正向影响比RP16的更大。

在图9中对比了本文计算的RN4反应（图中黑色实线与虚线）与SERINYEL等[15]使用的正丙醚相同反应的速率常数（图中黑色点线）。SERINYEL等借用了乙醚一级加氧产物ROO氢转移反应的速率常数, 用于正丙醚二级加氧产物OOQOOH氢转移裂解反应。图中可见, 该反应速率与本文中不考虑多结构效应获得的计算结果较为接近（黑色虚线）, 而与考虑多结构效应后的结果有明显偏差（黑色实线）。这是由于, 相比于乙醚, 丙醚的碳链更长, 碳基团之间的振-转耦合作用更强, 空间异构构象的复杂度更高, 对速率常数的影响更为突出。由此也说明, 开展OOQOOH氢转移裂解反应速率常数的详细计算的必要性。同时, 也与XING等[30]针对二乙醚自由基二级加氧反应产物的氢转移裂解反应速率常数（图9, 红色方块）以及SAKAI等[10]针对二乙醚自由基一级加氧产物ROO氢转移反应（图9, 红色三角）的速率常数进行了比较。由图可见, 文献中二乙醚的结果与本文中相似反应的未考虑多结构效应的计算结果十分接近。由于丙醚的OOQOOH的多结构效应较为显著, 对速率常数有明显影响。

进一步, 将获得的三个基元反应的速率常数拟合成阿伦尼乌斯公式, 获得了指前因子A、温度指数n和活化能Ea, 如表3所示。表3中的数据可以直接用于完善丙醚详细低温氧化动力学机理。

表3 高压极限下的速率拟合阿伦尼乌斯三参数 Table 3 Rate fitting of Arrhenius three parameters under high pressure limit
3 结论

利用量子化学方法构建了三种典型丙醚二级加氧反应产物OOQOOH发生氢转移反应生成氢过氧化物醛酮类物质和OH基的势能面, 结果表明, 异丙醚的关联产物的反应势能垒最低。

考虑了物种的多重构象影响, 获得了反应物的配分函数, 进一步计算了298 ~ 1 200 K范围内的热力学数据。结果表明, 考虑多重构象效应时获得的焓值比不考虑时平均高8.3 kJ/mol。熵和定压比热容的差异也较为明显。

最后, 基于过渡态理论, 获得了三个基元反应的速率常数, 并拟合成可用于构建详细反应机理的阿伦尼乌斯形式, 获得了指前因子、温度指数和活化能三个参数。对比结果表明, 考虑多结构效应后, 速率常数降低10 ~ 100 倍。本文提供了计算结果小于文献中利用类比法获得的结果, 表明考虑多结构效应对二级加氧产物进一步裂解反应的速率常数的显著影响, 获得的速率常数更具可靠性。

参考文献
[1] 方雪昀. 传统能源企业向清洁能源转型的驱动因素与策略研究[J]. 商讯, 2023(24): 29-32. [本文引用:1]
[2] 王涛, 王小琛, 赵鹏云, 等. 柴油双喷射撞击喷雾和燃烧可视化研究[J]. 内燃机工程, 2023, 44(6): 28-37. DOI:10.13949/j.cnki.nrjgc.2023.06.004. [本文引用:1]
[3] 任露, 焦宇飞, 董素荣, 等. 含氧燃料在柴油机上的应用研究新进展[J]. 内燃机与配件, 2018(24): 201-204. DOI:10.19475/j.cnki.issn1674-957x.2018.24.103. [本文引用:1]
[4] HOANG A T, MURUGESAN P, ELUMALAI P, et al. Strategic combination of waste plastic/tire pyrolysis oil with biodiesel for natural gas-enriched HCCI engine: experimental analysis and machine learning model[J]. Energy, 2023, 280: 128233. DOI:10.1016/j.energy.2023.128233. [本文引用:1]
[5] XU L J, WANG F F, LI M, et al. Fabrication and abrasive wear property of high chromium cast iron with high vanadium and high nitrogen content (HCCI-VN)[J]. Wear, 2023, 523: 204828. DOI:10.1016/J.WEAR.2023.204828. [本文引用:1]
[6] DISASSA H D, ANCHA V R, NALLAMOTHU R B, et al. Experimental study on the effect of speed and port-injected fuel blend ratio on a reactivity-control compression ignition (RCCI) engine performance[J]. Energy conversion and management: X, 2023, 20: 100448. DOI:10.1016/j.ecmx.2023.100448. [本文引用:1]
[7] GAINEY B, LAWLER B. The role of alcohol biofuels in advanced combustion: an analysis[J]. Fuel, 2021, 283: 118915. DOI:10.1016/j.fuel.2020.118915. [本文引用:1]
[8] SUN W Y, WANG G Q, LI S, et al. Speciation and the laminar burning velocities of poly(oxymethylene) dimethyl ether 3 (POMDME3) flames: an experimental and modeling study[J]. Proceedings of the combustion institute, 2017, 36(1): 1269-1278. DOI:10.1016/j.proci.2016.05.058. [本文引用:1]
[9] LUO Y, HE Y T, LIU C Z, et al. Combustion characteristics of biodiesel with different dimethyl ether blending strategies[J]. Fuel, 2023, 332: 126078. DOI:10.1016/j.fuel.2022.126078. [本文引用:1]
[10] SAKAI Y, ANDO H, CHAKRAVARTY H K, et al. A computational study on the kinetics of unimolecular reactions of ethoxyethylperoxy radicals employing CTST and VTST[J]. Proceedings of the combustion institute, 2015, 35(1): 161-169. DOI:10.1016/J.PROCI.2014.05.099. [本文引用:2]
[11] SERINYEL Z, LAILLIAU M, DAYMA G, et al. A high pressure oxidation study of di-n-propyl ether[J]. Fuel, 2020, 263: 116554. DOI:10.1016/j.fuel.2019.116554. [本文引用:2]
[12] SERINYEL Z, LAILLIAU M, DAYMA G, et al. A detailed high-pressure oxidation study of di-isopropyl ether[J]. Proceedings of the combustion institute, 2023, 39(1): 561-569. DOI:10.1016/j.proci.2022.07.038. [本文引用:2]
[13] UYUMAZ A, AYDOĞAN B, CALAM A, et al. The effects of diisopropyl ether on combustion, performance, emissions and operating range in a HCCI engine[J]. Fuel, 2020, 265: 116919. DOI:10.1016/j.fuel.2019.116919. [本文引用:1]
[14] 范学峰, 刘仲铠, 杨斌. 正丙醚低温氧化特性的反应机理研究[J]. 工程热物理学报, 2021, 42(8): 2169-2174. [本文引用:1]
[15] SERINYEL Z, LAILLIAU M, THION S, et al. An experimental chemical kinetic study of the oxidation of diethyl ether in a jet-stirred reactor and comprehensive modeling[J]. Combustion and flame, 2018, 193: 453-462. DOI:10.1016/j.combustflame.2018.04.002. [本文引用:2]
[16] XU X F, PAPAJAK E, ZHENG J J, et al. Multi-structural variational transition state theory: kinetics of the 1, 5-hydrogen shift isomerization of the 1-butoxyl radical including all structures and torsional anharmonicity[J]. Physical chemistry chemical physics, 2012, 14(12): 4204-4216. DOI:10.1039/c2cp23692c. [本文引用:1]
[17] BELHADJ N, BENOIT R, DAGAUT P, et al. Oxidation of di-n-propyl ether: characterization of low-temperature products[J]. Proceedings of the combustion institute, 2021, 38(1): 337-344. DOI:10.1016/j.proci.2020.06.350. [本文引用:1]
[18] XING L L, WANG Z D, TRUHLAR D G. Multistructural anharmonicity controls the radical generation process in biofuel combustion[J]. Journal of the American chemical society, 2019, 141(46): 18531-18543. DOI:10.1021/jacs.9b09194. [本文引用:1]
[19] 邢利利. 典型替代燃料的低温氧化反应动力学理论研究[D]. 合肥: 中国科学技术大学, 2017. [本文引用:1]
[20] XING L L, BAO J L, WANG Z D, et al. Relative rates of hydrogen shift isomerizations depend strongly on multiple-structure anharmonicity[J]. Journal of the American chemical society, 2018, 140(50): 17556-17570. DOI:10.1021/jacs.8b09381. [本文引用:1]
[21] ADLER T B, KNIZIA G, WERNER H J. A simple and efficient CCSD(T)-F12 approximation[J]. The journal of chemical physics, 2007, 127(22): 221106. DOI:10.1063/1.2817618. [本文引用:1]
[22] KNIZIA G, ADLER T B, WERNER H J. Simplified CCSD(T)-F12 methods: theory and benchmarks[J]. The journal of chemical physics, 2009, 130(5): 054104. DOI:10.1063/1.3054300. [本文引用:1]
[23] ZHAO Y, SCHULTZ N E, TRUHLAR D G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions[J]. Journal of chemical theory and computation, 2006, 2(2): 364-382. DOI:10.1021/ct0502763. [本文引用:1]
[24] CHAI J D, HEAD-GORDON M. Long-range corrected double-hybrid density functionals[J]. The journal of chemical physics, 2009, 131(17): 174105. DOI:10.1063/1.3244209. [本文引用:1]
[25] PAPAJAK E, TRUHLAR D G. Convergent partially augmented basis sets for Post-Hartree-Fock calculations of molecular properties and reaction barrier heights[J]. Journal of chemical theory and computation, 2011, 7(1): 10-18. DOI:10.1021/ct1005533. [本文引用:1]
[26] ZHENG J J, MIELKE S L, CLARKSON K L, et al. MSTor computer program[R]. Minneapolis: University of Minnesota, Minneapolis, CPC Program Library, 2012. [本文引用:1]
[27] ZHENG J J, MIELKE S L, CLARKSON K L, et al. MSTor computer program[R]. Minneapolis: University of Minnesota, Minneapolis, 2013. [本文引用:1]
[28] NEESE F. The ORCA program system[J]. WIREs computational molecular science, 2012, 2(1): 73-78. DOI:10.1002/wcms.81. [本文引用:1]
[29] NEESE F. Software update: the ORCA program system, version 4. 0[J]. WIREs computational molecular science, 2018, 8(1): e1327. DOI:10.1002/wcms.1327. [本文引用:1]
[30] XING L L, LIAN L C, WANG X T, et al. Hydrogen shift isomerizations in the kinetics of the first and second oxidation mechanism of diethyl ether combustion[J]. Computational and theoretical chemistry, 2021, 1202: 113340. DOI:10.1016/j.comptc.2021.113340. [本文引用:1]