采用的研究模型为棱长40 mm的含针翅的复合石蜡腔体, 在其加热表面分别布置数量、尺寸、排布方式均相同的铜材质导热针翅。由于在之前的模拟中针翅越长, 导热作用越明显, 但会在一定程度上抑制腔体中的自然对流作用。为更好地展示复合方腔中对流作用对石蜡融化的影响, 选用高度为20 mm、底面直径d为4 mm的柱状针翅, 共计16根, 且均匀分布在加热面上。设定三种工况：工况1为腔体上方加热, 并在上方布置针翅; 工况2为腔体左侧加热, 并在左侧布置针翅; 工况3为腔体下方加热, 并在下方布置针翅。位于加热面四角的针翅距离加热面边界均为8 mm, 相邻针翅纵、横间距均为8 mm, 工况示意图和针翅的分布情况如图1所示。选取纯石蜡方腔底部加热作为对比进行分析。铜和石蜡的物性参数见表1。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 不同工况示意图和针翅分布图Fig. 1 Schematic diagram of different working conditions and distribution of needle fins

表1

Table 1

表1(Table 1)

表1 铜和石蜡的物性参数 Table 1 Physical parameters of copper and paraffin wax 材料 参数 数值 铜 比热容/[J/(kg∙ K)] 385.00 密度/(kg/m3) 8 960.00 热导率/[W(m∙ K)] 400.00 石蜡 相变温度/K 308.15 固相密度/(kg/m3) 900.00 液相密度/(kg/m3) 850.00 固相热导率/[W/(m∙ K)] 0.22 液相热导率/[W/(m∙ K)] 0.13 固相比热容/[J/(kg∙ K)] 1 780.00 液相比热容/[J/(kg∙ K)] 2 146.70 相变潜热/(kJ/kg) 113.00 体膨胀系数/K-1 0.09 × 10-3

表1 铜和石蜡的物性参数 Table 1 Physical parameters of copper and paraffin wax

在模拟时, 石蜡腔体和针翅的初始温度设置为298.15 K, 加热壁面的温度为338.15 K。由于35号石蜡相变温度为308.15 K, 取相变温度区间为303.15 ~ 313.15 K, 除加热壁面外其余壁面均视作热绝缘界面, 在模拟过程中考虑了重力影响。

由于添加针翅的石蜡腔体内部融化传热过程十分复杂, 为了便于计算进行以下假设：

（1）假定石蜡液体不可压缩, 并且在腔体内做非稳态层流流动;

（2）液态石蜡符合Boussinesq假设, 并且以此模拟浮力引起的自然对流;

（3）在传热过程中, 忽略加热面热阻、石蜡黏性耗散和内部热辐射的影响;

（4）规定石蜡和针翅物性参数为常数, 不随传热过程而改变。

基于上述假设, 对石蜡腔体针翅进行数值模拟, 其融化传热过程中的控制方程如下。

连续性方程：

$\frac{\partial \rho }{\partial t}+\frac{\partial \left( \rho u \right)}{\partial x}+\frac{\partial \left( \rho v \right)}{\partial y}+\frac{\partial \left( \rho w \right)}{\partial z}=0$ (1)

式中：u、v、w分别为x、y、z轴上的速度分量, m/s; ρ 为石蜡密度, kg/m³。

能量方程：

$\rho \left( \frac{\partial H}{\partial t}+u\frac{\partial H}{\partial x}+v\frac{\partial H}{\partial y}+w\frac{\partial H}{\partial z} \right)=\frac{\lambda }{{{C}_{p}}}\left( \frac{{{\partial }^{2}}H}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}H}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}H}{\partial {{z}^{2}}} \right)+\frac{\rho }{{{C}_{p}}}\cdot \frac{\partial H}{\partial t}$ (2)

式中：H为石蜡的相变比焓, J/kg; C_p为石蜡的定压热容, J/(kg∙ K); λ 为石蜡的导热系数, W/(m∙ K)。

动量方程：

$\rho \left( \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z} \right)=\mu \left( \frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{z}^{2}}} \right)-\frac{\partial p}{\partial y}+{{S}_{v}}$ (3)

$\rho \left( \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} \right)=\mu \left( \frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}} \right)-\frac{\partial p}{\partial x}+{{S}_{u}}$ (4)

$\rho \left( \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z} \right)=\mu \left( \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}w}{\partial {{z}^{2}}} \right)-\frac{\partial p}{\partial z}+{{S}_{w}}$ (5)

式中：p为石蜡的绝对压力, Pa; μ 为石蜡的动力黏度, 取0.043 4 Pa∙ s; S_u、S_v、S_w分别为x、y、z轴上施加的源项。

源项方程：

${{S}_{u}}=\frac{\left( 1-{{\beta }^{2}} \right)}{\left( {{\beta }^{2}}+\varepsilon \right)}{{A}_{\text{mush}}}u$ (6)

${{S}_{v}}=\frac{\left( 1-{{\beta }^{2}} \right)}{\left( {{\beta }^{2}}+\varepsilon \right)}{{A}_{\text{mush}}}v$ (7)

${{S}_{w}}=\frac{\left( 1-{{\beta }^{2}} \right)}{\left( {{\beta }^{2}}+\varepsilon \right)}{{A}_{\text{mush}}}w+\rho g\alpha \left( T-{{T}_{0}} \right)$ (8)

式中：ε 为防止分母为零添加的系数, 取1 × 10^-3; A_mush为糊状区连续参数, 取5 × 10⁴; α 为石蜡的体膨胀系数, K^-1, 取0.09 × 10^-3 K^-1; $\beta $为液相率; g为重力加速度, 9.8 m/s²; T为过程中任意时刻的温度, K; T₀为初始时刻的温度, K。

液相率计算公式：

$\beta =\left\{ \begin{matrix} 0 \\ \frac{\left( T-{{T}_{\text{s}}} \right)}{\left( {{T}_{\text{l}}}-{{T}_{\text{s}}} \right)} \\ 1 \\ \end{matrix} \right.\begin{matrix} \quad \left( T< {{T}_{\text{s}}} \right) \\ \quad \quad \quad \left( {{T}_{\text{s}}}< T< {{T}_{\text{l}}} \right) \\ \quad \left( {{T}_{\text{l}}}< T \right) \\ \end{matrix}$ (9)

式中：T_s为石蜡相变开始温度, K; T_l为石蜡相变停止温度, K。

平均努塞尔数（Nu）计算公式：

$Nu=\frac{hl}{{{\lambda }_{\text{pcm}}}}$ (10)

$h=\frac{{{Q}_{\text{total}}}}{A\left( {{T}_{\text{h}}}-{{T}_{\text{c}}} \right)\, {{t}_{n}}}$ (11)

傅里叶数（Fo）计算公式：

$Fo=\frac{{{\lambda }_{\text{pcm}}}}{\rho {{C}_{p}}}\cdot \frac{{{t}_{n}}}{{{L}^{2}}}$ (12)

式中：h为对流换热系数, W/(m²∙ K); l为壁面特征尺寸, m; λ _pcm为液相石蜡的导热系数, W/(m∙ K); Q_total为通过的总热量, J; A为流通面积, m²; T_h为加热温度, K; T_c为相变中心温度, K; t_n为融化过程进行的时间, s; L为加热面特征尺寸, m。

复合腔体的储热量、平均储热速率计算公式：

$Q=\left( {{T}_{\text{c}}}-{{T}_{0}} \right){{m}_{\text{p, s}}}{{C}_{p\text{, s}}}+\left( {{T}_{\text{ave}}}-{{T}_{\text{c}}} \right){{m}_{\text{p, l}}}{{C}_{p, \text{l}}}+{{m}_{\text{p, l}}}h+\left( {{T}_{\text{ave}}}-{{T}_{0}} \right){{m}_{\text{f}}}{{C}_{p, \text{f}}}$ (13)

${{P}_{\text{ave}}}=\frac{Q}{{{t}_{n}}}$ (14)

式中：m_{p, s}为固相石蜡质量, kg; m_{p, l}为液相石蜡质量, kg; T_ave为相变完成时刻平均温度, K; C_{p, s}、C_{p, l}分别为固相石蜡和液相石蜡的定压比热容, J/(kg∙ K); m_f为金属针翅的质量, kg; C_{p, f}为金属针翅的比热容, J/(kg∙ K)。

有限元软件通过将复杂结构或系统分割成大量小网格, 并在这些网格节点上建立方程, 在一定的时间步长上近似求解。网格划分越细致、时间步长越小, 计算越精确, 但计算时间就会越长。反之, 则相反。为选取更为合适的网格划分方式和时间步长, 同时证明网格、时间步长对模拟结果的影响可以忽略, 现进行无关化验证。

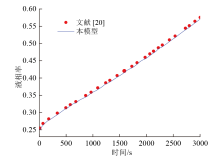
以工况1为例, 对石蜡腔体的液相率进行求解验证。采用三种不同精度的网格划分, 其对应的网格数分别为201 036个、536 900个、1 262 364个。图2为不同网格数下液相率与时间的关系曲线。结果表明, 三种网格划分方式下液相率曲线无明显差异, 三种划分方式的石蜡均在约4 000 s时完全融化。第二种划分方式与第一、三种划分方式的液相率平均误差分别为0.14%和0.06%。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 网格无关性验证Fig. 2 Verification of grid independence

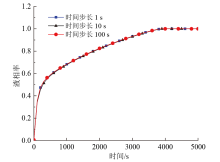
在选取合适的时间步长时, 分别设定了1、10、100 s三种时间步长。图3为不同时间步长条件下, 液相率随时间的变化曲线。由图可知, 液相率曲线趋势并无明显差别, 通过计算发现, 每10 s一个时间步长与每1 s、100 s一个时间步长的液相率平均误差分别为0.5%和0.61%。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 时间步长无关性验证Fig. 3 Verification of time step independence

综上所述, 为了兼顾本模拟的计算精度与准确性, 选取网格数536 900个、每10 s一个时间步长进行数值模拟。

为确保模拟的准确性, 本文与文献[20]进行模拟对比。文献[20]是在三维腔体中加入相变材料, 并且向相变腔体中添加不同体积分数的铝纳米颗粒, 数值模拟腔体内相变过程, 分析材料的融化特性。本文与文献的模型均为三维模型, 采用文献中边界条件进行模拟：左壁面加热40 ℃、其余壁面无滑移并且绝热、添加颗粒体积分数为0%, 即纯石蜡进行模拟验证。数值模拟得到了液相率随时间变化的曲线, 如图4所示。模拟结果与文献的结果基本一致, 模型验证的平均误差小于5%, 从而证明了本文计算模型的合理性。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 模型验证Fig. 4 Model validation

为了分析石蜡的融化过程, 引入液相率进行描述, 见式（9）。石蜡液相率是液相石蜡占石蜡总体积的比值, 液相率越大说明液相石蜡体积越大, 融化过程越深入。液相率为1时, 石蜡为液相, 液相率为0时, 为石蜡固相。

图5为在加热第100、300、500 s时, 分别在x = 20 mm、y = 20 mm处截取的yoz、xoz交叉平面的不同工况下复合石蜡腔体的液相分布云图, 图6为不同工况液相率随时间变化的曲线图。由液相率随时间变化的曲线可知, 在开始加热的第100 s时, 工况1、工况2、工况3和纯石蜡的液相率分别为0.34、0.35、0.37、0.10。此时, 热量由高温壁面快速传导到针翅, 较为均匀地排布在针翅根部, 相场分布非常相似, 针翅顶端的固相石蜡呈锯齿状分布。在加热第300 s时, 工况1的固液相交界线相对平滑, 只有部分区域的石蜡完全融化, 其中液相石蜡均分布在方腔上部, 液相率为0.51。工况2的液相石蜡主要分布在腔体上部, 由上向下逐渐减少, 液相率为0.60; 工况3中液相界面呈抛物线形状分布在腔体的中下部, 此时石蜡融化已经过半, 液相率为0.67。在加热第500 s时, 工况1出现了热量封锁现象, 热量全部集中在含有针翅的上半部分, 液相石蜡全部集中在方腔的中上部; 工况3固相石蜡基本融化完毕, 液相率为0.94。分析表明左侧加热且布置针翅和下方加热且布置针翅的融化速率都比纯石蜡融化效率高, 采取上方布置加热面会严重阻碍腔体内石蜡液体自然对流的形成, 完全融化时间比纯石蜡完全融化时间延长了1 610 s, 减缓了整个石蜡腔体的完全融化过程。

图5

Fig. 5

	Figure Option ViewDownloadNew Window
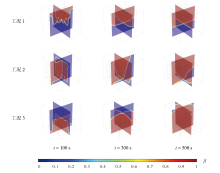	图5 不同工况下复合石蜡腔体的液相率云图Fig. 5 Liquid phase rate cloud for different working conditions of composite paraffin cavity

图6

Fig. 6

	Figure Option ViewDownloadNew Window
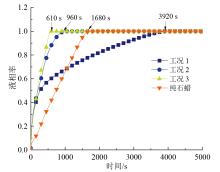	图6 不同工况下复合石蜡腔体的液相率曲线Fig. 6 Liquid fraction graph for different working conditions of composite paraffin cavity

由图6可知, 工况1融化时间最长, 为3 920 s; 工况2融化时间在二者之间, 960 s左右达到完全融化; 工况3融化时间最短, 610 s左右就已经完全融化。结果表明, 在腔体上方布置加热面和针翅抑制了腔体内热对流的发展与形成, 使腔体内部的相变材料只能通过导热的方式进行传热, 不利于整个融化过程的进行。在腔体下方布置加热面和针翅能够最大程度地促进自然对流的形成与发展, 针翅的存在可以显著增强相变材料周围流体的流动, 从而促进整个石蜡腔体的热对流过程, 热量可以更快速地通过热对流的方式传递给腔体内部的相变材料, 使其快速融化。

图7为在加热第100、300、500 s时, 在y = 20 mm处截取的xoz平面的不同工况下复合石蜡腔体的温度分布云图。由图可知, 在加热前期的第100 s时, 由于针翅的高导热性, 热量可以快速传导至腔体内部, 使得三种工况仅壁面和针翅区域的温度较高, 其余部分的石蜡腔体温度较低。在加热第300 s时, 工况1中, 高温区域只集中在方腔上部, 高低温区域有着明显的分界线, 并且高温区域未超过针翅顶部, 温度约为327.18 K; 工况2中, 高温区域主要分布在腔体上部, 随着高度的降低, 高温区域逐渐减小, 到腔体底部时, 只有壁面处温度较高, 低温区域主要集中在腔体的右下部; 工况3中, 高温区域呈对称式分布且温度分布均匀, 针翅端部区域温度约为338.13 K。在加热第500 s时, 工况1的整个腔体温度分布与第300 s时类似, 但是高温区域与低温区域的分界线更为平直, 能显著地区分出高低温区域; 工况2中, 超过多半的区域温度达到338 K, 低温区只集中在底部边角的区域, 称为死区部分; 工况3中, 腔体顶部四块边角区域温度较低, 其他区域温度分布十分均匀, 腔体中心温度约为338 K。

图7

Fig. 7

	Figure Option ViewDownloadNew Window
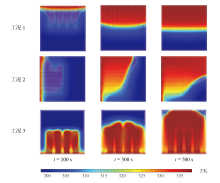	图7 不同工况下复合石蜡腔体的温度分布云图Fig. 7 Temperature cloud for different working conditions of composite paraffin cavity

结果表明, 在加热过程中, 热量首先由壁面传导至金属针翅, 随后通过金属针翅导入石蜡腔体, 石蜡受热逐渐融化, 腔体内的温度随之升高。液相石蜡的热对流效应对温度分布影响较大, 加热面和针翅在下方时, 热对流作用更容易形成, 腔体温度分布更为均匀。而加热面和针翅位在上方时, 由于热流体密度相对固相石蜡密度较小的缘故, 较高温度的液相石蜡只集中分布于腔体上层, 与下半部分无法形成热对流, 腔体底部的固相石蜡依靠导热传递热量, 石蜡的导热系数又非常低, 从而导致高低温区域形成明显的两极分化。

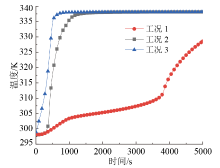
图8为各工况下复合石蜡腔体平均温度的上升曲线。由图可知, 工况1的温度呈逐渐上升的趋势, 但是温度上升较为缓慢, 在5 000 s时温度还未达到338 K, 前1 000 s的温升速率仅为5.25 K/s。这是由于方腔底部存在着低温固相石蜡, 重力对形成对流循环的助益较小, 导致温度上升较慢, 这一部分区域并没有得到充分的加热, 导致体平均温度较低。工况2的温度曲线启动比工况1慢约200 s, 但在1 500 s时温度达到338 K, 前1 000 s温升速率为37.40 K/s。工况3启动最快、升温最快, 在加热第910 s时就已经达到338 K, 前1 000 s平均温升速率为39.89 K/s。由此可知合理布置针翅以及加热面能使热量更加有效地在整个腔体内部传播, 对PCM温度分布均匀性影响较大。

图8

Fig. 8

	Figure Option ViewDownloadNew Window
	图8 不同工况下复合石蜡腔体的平均温度曲线Fig. 8 Average temperature curve for different working conditions of composite paraffin cavity

图9为在加热第100、300、500 s时, 在y = 20 mm处截取的xoz平面的不同工况下复合腔体的液相石蜡流动速度分布云图。由图可知, 在加热第100 s时, 所有工况的速度分布现象趋于一致, 融化后流速较高的石蜡液体分布在针翅之间, 均没有超出针翅顶端进入方腔深处。在加热第300 s时, 工况1中, 只有针翅顶端的液相石蜡流速较大, 其他部分的液相石蜡流速较低; 工况2中, 腔体顶部高流速区域较大, 腔体由上至下高流速区域逐渐减小; 工况3中, 腔体中下部液相石蜡流速较大且分布均匀, 流速约为6.077 4 × 10^-4 m/s。在加热第500 s时, 工况1由于加热面位于上方, 固体石蜡在腔体底部, 未能有效促进冷热流体的自然对流, 因此速度逐渐降低, 约为3.129 3 × 10^-4 m/s; 工况2中, 液相石蜡流速较高的区域主要分布在腔体中上部, 底部流速逐渐降低; 工况3的整个腔体加热充分, 高流速液相石蜡均匀布满腔体, 速度约为1.227 2 × 10^-3 m/s。

图9

Fig. 9

	Figure Option ViewDownloadNew Window
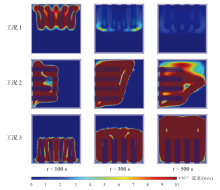	图9 不同工况下复合腔体的液相石蜡流动速度分布云图Fig. 9 Velocity cloud for different working conditions of liquid paraffin in composite cavity

结果表明, 在加热初期, 热量通过高导热针翅快速且均匀地传导至石蜡腔体浅层表面, 使得靠近针翅之间的固相石蜡快速地融化为液相石蜡, 液相石蜡流速逐渐增加。随着加热过程的进行, 更多的固相石蜡开始融化为液相石蜡。由于热对流原因, 液相石蜡部分受热, 温度高的液相石蜡密度减小, 向上升; 而温度较低、密度较大的液相石蜡则下沉, 形成热对流。加热面和针翅在下方最有利于自然对流的形成, 加热面和针翅在上方时最不利于冷热对流的形成, 才会导致液相石蜡两种截然不同的速度分布。加热面和针翅在左侧时, 腔体中形成由上至下的环流, 上方高流速区域大, 因此腔体上半部分石蜡融化的多, 底部融化较少。

为了更直观地分析不同工况下石蜡融化过程中自然对流的影响, 引入表征石蜡融化过程中自然对流强度的无量纲Nu和无量纲时间Fo进行分析, 见式（10 ~ 12）。

图10展示了不同布置方式对加热面对向壁面Nu的影响, 从整体上看工况1的Nu值一直保持在较低水平, 而工况2、3的Nu曲线随着Fo的增加先达到峰值再逐渐减小。加热过程刚开始, 热量并没有到达加热面的对向壁面, 因此在Fo约为0.016时, 三种工况的Nu均保持在1不变。工况1中, 加热面和针翅布置在方腔顶部, 抑制了石蜡融化后由密度差引起的自然对流, 温度较高的顶部区域只能通过导热的方式将热量传递到腔体底部低温区域, 在整个融化过程中几乎全部依靠导热传递热量, 因此Nu稳定趋于1。工况2中, 腔体顶部最先形成自然环流, 自左向右、自上而下发展液相石蜡的对流区域, 顶部的热流体先到达对向壁面, 因此Nu会比工况3提前增加。工况2最大峰值在Fo为0.019时, Nu为1.92。工况3由于底部加热使底边两侧最易形成瑞利-贝纳德对流, 小环流区域逐渐向中间靠拢、向上发展, 在Fo = 0.024时, Nu达到峰值5.65。随着加热过程的进行, 通过对向壁面的热量不断减小, 即Nu逐渐降低, Fo到达0.15之后整个加热过程更为稳定, 三种工况的Nu逐渐趋于稳定, 并不断接近于1, 表明由对流作用占主导的传热方式向热传导转变。

图10

Fig. 10

	Figure Option ViewDownloadNew Window
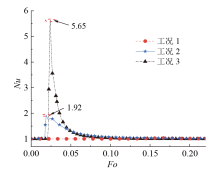	图10 不同工况下复合腔体的对向壁面NuFig. 10 Nusselt number of opposite wall surfaces for different working conditions of composite paraffin cavity

综上所述, 下方布置加热面和针翅时, 底部加热导致热的液相石蜡向上运动, 冷流体从四周下沉, 重力作用让液相石蜡下沉时更有优势, 最利于自然对流的形成以及对流区域的发展。左壁面布置加热面和针翅介于顶面布置和底面布置两种工况之间, 其效果优于顶部布置加热面和针翅。上方布置加热面和针翅时高温液相石蜡被封锁在腔体上部, 抑制腔体形成自然对流, 只能依靠纯导热传递热量几乎不体现对流作用, 其Nu数值一直保持较低水平。

复合腔体的储热速率是储热的关键指标之一, 完全储热所需时间越短说明储热速率越大, 即单位时间内储热越多, 以此为依据对不同工况进行储能效果分析, 引入储热量、储热速率分析指标, 见式（13）、式（14）。

添加16根针翅能够增加约4 220.16 mm²的换热面积, 能够加快热量的传导和储存。整个复合腔体中的石蜡以及金属针翅的体积分数保持一致, 因此针翅所增加的换热面积在各工况中相同。由于完全融化时的体中心温度是不同的, 因此三种工况的储热量存在差异。工况1、工况2、工况3完全融化时的储热量分别为9.49、10.22、10.09 kJ。工况3比工况1增加了6.3%的储热容量。图11展示了不同位置布置加热面和针翅腔体储热量、储热速率、完全融化时间的数据, 工况1石蜡腔体完全融化时间最长, 储热速率最小, 仅为2.42 W; 工况2融化时间为960 s, 储热量最大10.22 kJ; 工况3腔体完全融化时间最短, 为610 s, 储热速率达到了16.55 W, 是工况1的6.84倍, 是工况2的1.56倍, 储热速率最大。结果表明在下方布置加热面和针翅相较于其他两种工况能够更好地促进自然对流的形成, 强化腔体内部换热效率, 加快石蜡的融化, 最大限度地提高储热速率。同时, 添加金属针翅可以增加一部分高导热面积, 进一步提高整个腔体的传热速度, 促进整个相变储热过程的快速进行。

图11

Fig. 11

	Figure Option ViewDownloadNew Window
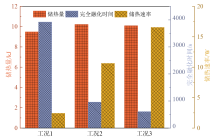	图11 针翅布置对复合方腔储热效果的影响Fig. 11 Impact of needle-fin arrangement on heat storage effect of composite paraffin cavity

向石蜡基相变储热材料中添加高导热翅片, 有效提升了储热速率, 对于建筑节能和太阳能热利用系统的热效率提升尤为关键。未来, 该技术在电力系统储能、电动汽车电池热管理和航空航天器的精确热控制等新兴领域, 因其出色的储热特性, 有着更广泛的应用潜力。