1.1.1 风力机几何模型

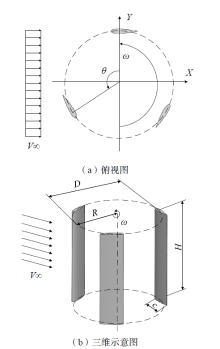
用于CFD计算结果验证的垂直轴风力机是参照ELKHOURY等^[10]的试验模型建立的, 风力机模型相关几何参数列于表1。图1为风力机模型的俯视图及三维示意图。

表1

Table 1

表1(Table 1)

表1 风力机结构参数 Table 1 Structural parameters of the wind turbine 参数 数值 叶轮直径D/mm 800 叶片高度H/mm 800 叶片弦长c/mm 200 叶片数量n 3 叶轮实度σ 0.75 叶片翼型 NACA 0018

表1 风力机结构参数 Table 1 Structural parameters of the wind turbine

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 风力机模型示意图Fig. 1 Schematic diagram of the wind turbine model

CFD数值计算结果验证是确保实验对象性能评估准确性的关键步骤。通过将CFD模拟得到的风力机性能参数与ELKHOURY等的试验数据进行比较能够确认数值模型的可靠性。这种验证不仅为后续的优化研究提供了一个可信的预测工具, 而且允许在不进行实际物理测试的情况下, 对风力机的设计进行快速迭代和性能评估。

1.1.2 计算域及边界条件设置

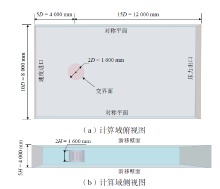
采用STAR-CCM+ 进行仿真计算, 计算域示意图如图2所示。该三维计算域由一个固定的长方体区域和一个圆柱体重叠区域组成, 计算域尺寸为20D × 10D × 5H, 重叠区域高度为2H, 直径为2D, 其中D为叶轮直径, H为叶片高度。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 计算域示意图Fig. 2 Schematic diagram of calculation domain

在计算域中, 速度进口设置为U₀ = 8 m/s的流速, 压力出口设置为P₀ = 0.0 Pa的恒定压力。动力黏度为1.855 08 × 10^-5 Pa∙ s, 相应的湍流速度尺度、湍流黏度比、湍流强度分别设置为1 m/s、10、0.8%。左右边界被设定为对称平面, 以避免边界反射; 上下边界被设定为滑移壁面, 叶片设置为无滑移壁面。

1.1.3 网格划分及求解器设置

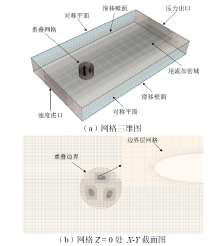
计算域均为棱柱层网格, 对叶轮旋转区域及尾流区域进行不同层次加密。采用重叠网格模拟垂直轴风力机旋转运动。在叶片附近生成高分辨率网格以保证边界流动的准确模拟, 创建尾迹加密区域以获得更详细的尾流场信息, 如图3所示。基于进口速度U₀ = 8 m/s及模型弦长c = 0.2 m的初始条件, 为了满足SST k-ω 对y+ < 1的要求, 棱柱层网格层数、增长率及总厚度分别设置为10层、1.25%和1.202 × 10^-3 m。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 计算域网格划分图Fig. 3 Grid division diagram of calculation domain

采用基于有限体积法的STAR-CCM+ 对三维非定常不可压缩流动进行数值模拟, 选择隐式非稳态分离流方法求解。采用SST k-ω 湍流模型求解Navier-Stokes方程。对流项采用二阶迎风格式, 时间离散采用二阶中心差分格式。利用重叠网格实现垂直轴风力机的旋转运动。

1.1.4 网格无关性验证

网格的质量和数量对预测风力机的空气动力学特性具有重要作用。考虑到风轮位于重叠区域, 为确保计算结果的准确性, 将重叠区域的网格尺寸设置为三个不同的值来计算不同网格精度下的功率系数（power coefficient, C_p）, 相关结果数据见表2。网格由中等细化到精细时, 相对误差（ε ）仅为0.4%, 进一步增加网格并不会提高结果精度。在综合考虑计算效率与精度的基础上, 选择中等分辨率的网格进行后续仿真。

表2

Table 2

表2(Table 2)

表2 不同网格精度下的网格数量、Cp值及相对误差 Table 2 Mesh number, Cp value and relative error under different mesh precision 网格精度 网格数量 计算Cp ε /% 粗糙 1 136 298 0.141 6 -18.0 中等 2 104 725 0.172 7 -0.4 精细 3 211 559 0.173 4 —

表2 不同网格精度下的网格数量、Cp值及相对误差 Table 2 Mesh number, Cp value and relative error under different mesh precision

1.1.5 风力机数值模型验证

数值仿真模拟结果与ELKHOURY等试验结果的对比如图4所示。从图中可以观察到, 本研究很好地复现了C_p随叶尖速比（λ ）的变化趋势, 与实验结果吻合良好。这表明当前的数值模型可以作为一种可靠的方法应用于后续的研究中。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
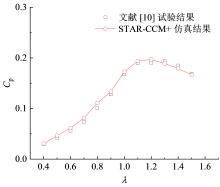	图4 CFD仿真结果与文献[10]试验结果对比Fig. 4 Comparison between CFD simulation result and test result

1.2.1 田口方法概念

田口方法的主要原理是基于质量损失函数, 利用参数偏离目标值的程度来评估产品质量优劣。实际工程里用信噪比（S/N比）代替质量损失函数对结果进行评估^[11]。S/N比越大, 表示品质特性受噪声因素的干扰越小, 产品质量越好。

如式（1）所示, y_i代表试验结果中的功率系数, S/N比越大, 则表示风力机风能利用率更高。

(1)

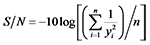式中：y_i为第i个工况的C_p值; n为试验样本总数。

1.2.2 正交工况设计

田口方法利用正交试验设计原则, 确保因素水平在试验空间中均匀分布, 实现因素间的全面对比。聚焦四因素四水平问题, 详细参数与水平配置见表3。相较于全因素试验所需的256个工况, 应用L16(4⁴) 正交表优化试验设计, 具体参数见表4, 仅需16个代表性工况, 显著提高了研究效率。

表3

Table 3

表3(Table 3)

表3 参数选择及水平设置 Table 3 Parameters selection and level setting 因素 参数 符号 水平 1 2 3 4 A 叶片数量 n 2 3 4 5 B 叶轮半径 R 1.0 1.5 2.0 2.5 C 叶片展弦比 μ 5 6 8 10 D 叶片安装角 β 0 3 6 9

表3 参数选择及水平设置 Table 3 Parameters selection and level setting

表4

Table 4

表4(Table 4)

表4 正交工况设计 Table 4 Orthogonal condition design 工况 因素 A B C D EC 1 2 1.0 5 0 EC 2 2 1.5 6 3 EC 3 2 2.0 8 6 EC 4 2 2.5 10 9 EC 5 3 1.0 6 6 EC 6 3 1.5 5 9 EC 7 3 2.0 10 0 EC 8 3 2.5 8 3 EC 9 4 1.0 8 9 EC 10 4 1.5 10 6 EC 11 4 2.0 5 3 EC 12 4 2.5 6 0 EC 13 5 1.0 10 3 EC 14 5 1.5 8 0 EC 15 5 2.0 6 9 EC 16 5 2.5 5 6

表4 正交工况设计 Table 4 Orthogonal condition design

1.2.3 广义加性模型

广义加性模型（generalized additive model, GAM）是一种灵活且应用广泛的统计模型, 用来估算因变量和多个自变量之间复杂的非线性关系, 基本形式见式（2）^[12]：

(2)

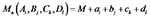式中：M_a为信噪比的估计值; M为正交试验中16次运行的平均S/N的平均值。下标i、j、k、l分别为与每个因子相关的水平, 其中a_i为正交试验表中A参数在i水平时的S/N比平均值与M的差值。

1.2.4 改进的加性模型

除了最初选定的因素外, 因素之间的交互作用也可能是影响垂直轴风力机（vertical axis wind turbine, VAWT）性能的重要因素。因此, 在田口方法的预测中必须考虑因素之间的交互作用。改进的加性模型（modified additive model, MAM）显示了两个因素之间的相互作用, 可以通过式（3）及式（4）来完成^[12]：

(3)

(4)

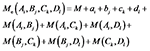式中：M_e为进一步考虑了因素间的交互作用后的信噪比估算值; M (A_i, B_j) 为同时包含i水平的参数A和j水平的参数B的所有工况对应的S/N比平均值。

不同工况下的额定尖速比λ _rated、风力机平均功率系数C_p及信噪比S/N的数据如表5所示。将四个因素的平均信噪比曲线绘制于图5。

表5

Table 5

表5(Table 5)

表5 正交试验工况中的计算结果 Table 5 Calculation results in orthogonal test conditions 工况 λ rated Cp S/N EC 1 1.1 0.187 8 -14.527 4 EC 2 2.1 0.298 9 -10.488 8 EC 3 2.7 0.335 5 -9.486 0 EC 4 3.1 0.323 2 -9.810 5 EC 5 1.3 0.251 2 -11.999 9 EC 6 1.5 0.308 6 -10.212 1 EC 7 2.3 0.322 0 -9.842 0 EC 8 2.4 0.374 6 -8.528 3 EC 9 1.1 0.228 7 -12.813 9 EC 10 1.7 0.290 3 -10.742 4 EC 11 1.8 0.251 3 -11.997 0 EC 12 2.3 0.274 5 -11.228 4 EC 13 1.0 0.184 4 -14.684 2 EC 14 1.6 0.185 8 -14.619 9 EC 15 1.7 0.281 3 -11.016 9 EC 16 1.7 0.316 0 -10.005 7

表5 正交试验工况中的计算结果 Table 5 Calculation results in orthogonal test conditions

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 四因素在不同水平上的平均信噪比值Fig. 5 Average signal-to-noise ratio of the four factors at different levels

结果显示, 参数A随着叶片数量的增加, 其平均信噪比首先从水平1上升至水平2的最大值, 随后持续下降, 表明叶片数量过多或过少都会对功率系数产生不利影响。参数B的平均信噪比值从水平1持续增加到水平4, 说明叶轮半径的增加对功率系数有积极影响。通过上述分析可知, 叶轮半径R对垂直轴风力机气动效率的影响最为显著, 这可以从叶轮半径在不同水平下信噪比的变化幅度中看出, 其变化幅度大于其他参数。具体来说, 影响程度排序依次为因素B（R）> 因素A（n）> 因素D（β ） > 因素C（μ ）。

采用GAM和MAM两种方法优化设计参数。首先通过GAM分析确定了不同设计参数下的最优和最差工况。然而, 这种方法未能考虑到参数间的交互作用, 可能导致预测结果不准确。为了解决这一问题, 引入了MAM模型, 该模型通过添加交互项来考虑参数间的交互作用, 从而提高了分析的精确度。通过MAM模型的分析, 得到了考虑参数交互后的最优和最差风力机结构, 列于表6, 并进行了仿真验证, 结果如图6所示。由图可知, 两台风力机的功率系数均随着叶尖速比的增大呈现出先增大后减小的趋势。MAM模型分析得出的最优模型在λ _rated= 2.4处达到最大平均功率系数0.374 6; 最差模型在λ _rated= 0.8处达到最大平均功率系数0.126 9。

表6

Table 6

表6(Table 6)

表6 改进的加性模型分析结果 Table 6 Analysis results of modified additive model 工况 A B C D 最优 3 2.5 8 3 最差 5 1.0 5 0

表6 改进的加性模型分析结果 Table 6 Analysis results of modified additive model

图6

Fig. 6

	Figure Option ViewDownloadNew Window
	图6 最优及最差构型风力机在不同叶尖速比下的功率系数Fig. 6 Power coefficients of optimal and worst wind turbines under different tip speed ratios

2.3.1 叶轮涡量场分析

在分析最优和最差构型的气动性能时, 涡量的分布情况提供了关键的洞察。最优构型[图7（a）]的叶片周围和风轮内部显示出较低的涡量水平, 且这些涡量呈现出均匀和有序的周期性分布。这种特征表明叶片与气流之间的相互作用更加协调, 促进了更高的能量转换效率。特别是在叶片中部与叶尖之间, 最优构型展现出明显的涡量梯度, 尽管叶尖部分产生较大涡量, 但中部区域涡量较小且稳定, 这有助于维持气流的流畅性。此外, 最优构型的负安装角有助于减少因动态失速而产生的涡流分离, 进一步降低了叶片间的相互干扰, 提升了气动效率。相比之下, 最差构型[图7（b）]由于较大的整体实度, 导致整个叶轮区域涡量显著增加, 叶片间产生的涡流发生强烈相互作用, 并伴随着高度不稳定性。这种强烈的涡流干扰和不稳定性导致了能量的损失, 从而降低了风力机的气动效率。整体而言, 最优构型在气动性能上优于最差构型, 主要归功于其较低的涡量水平、有序的涡量分布以及减少的叶片间干扰, 这些因素共同作用实现了更优的能量捕获和转换效率。

图7

Fig. 7

	Figure Option ViewDownloadNew Window
	图7 MAM最优构型λ = 2.4（a）和MAM最差构型λ = 0.8（b）的三维涡量图Fig. 7 Three-dimensional vorticity diagram under MAM optimal configuration λ = 2.4 (a) and MAM worst configuration λ = 0.8 (b)

2.3.2 叶轮尾流场分析

尾流速度云图可以展示风力机下游的流动特性。较小的速度亏损区域意味着较小的能量损失。在对比最优和最差构型的尾流速度云图（图8和图9）时, 可以观察到最优构型在下游区域速度亏损较小, 表明其能量损失较低, 流动特性更为理想。随着下游距离的增加, 最优构型的尾流速度逐渐减弱, 尤其是在叶片展弦的中部区域, 流速降低更为明显, 而两侧的低速区域则逐渐向两侧扩张, 显示出一种较为均匀的尾流发展趋势。尽管在X = 6D范围内速度亏损较为严重, 但整体而言, 最优构型展示出较小的速度亏损。相比之下, 最差构型在X = 6D的Y-Z平面中, 垂直轴风力机中部出现了较X = 4D更大的速度幅值亏损。从图9可以看出, 最差构型尾流速度影响范围达到10D左右, 在4D前出现了较为严重的速度亏损。这进一步凸显了最优构型在减少能量损失和改善尾流恢复方面的优越性。

图8

Fig. 8

	Figure Option ViewDownloadNew Window
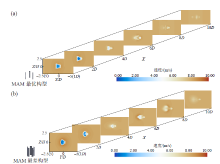	图8 MAM最优构型（a）和MAM最差构型（b）在Y-Z平面内不同距离处的尾流速度云图Fig. 8 Wake velocity cloud images of the MAM optimal configuration (a) and MAM worst configuration (b) at different distances in the Y-Z plane

图9

Fig. 9

	Figure Option ViewDownloadNew Window
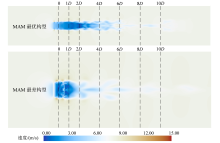	图9 MAM最优构型及MAM最差构型在X-Z平面内尾流速度云图Fig. 9 Wake velocity cloud images of the MAM optimal configuration and MAM worst configuration in the X-Z plane

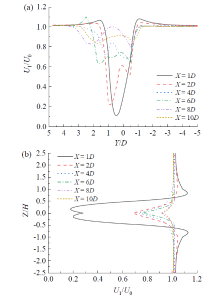
从图10、图11可以看出, 由于马格努斯效应致使风力机尾流在X-Y平面处偏离中心线, 但该现象随着尾迹距离的增加逐渐减弱。此外, 随着尾迹距离的增加, 同一平面内的速度亏损差值减小, 在X-Y平面中的影响范围逐渐扩大。从图10中可以观察到, 在X = 2D靠近中心处的速度亏损也要大于X = 1D处的值, 类似地还有在X = 6D靠近中心处的尾流速度恢复较快。造成该现象的原因可能是尾迹在发展过程中, 不同速度的涡相互作用或尾流与湍流场混合从而产生了混沌流动。在最优构型中, 尾迹速度亏损区域主要集中在X-Y平面中的 ± 1D及X-Z平面的 ± 1H附近, 周围区域的速度亏损较小, 这表明最优构型在减少能量损失和控制尾流影响范围方面表现更佳。相比之下, 图11可以观察到最差构型在X-Y平面上的影响范围更广, 从 -1D延伸至 +3D, 且在X-Z平面中的影响也较大, 这表明其尾流对下游气流的影响更显著, 导致更大的能量损失。因此, 最优构型通过较小的尾流影响范围和较低的速度亏损, 实现了更集中的能量转换, 减少了能量损失, 从而在气动性能上优于最差构型。

图10

Fig. 10

	Figure Option ViewDownloadNew Window
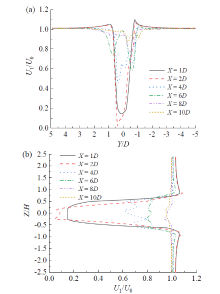	图10 最优构型不同距离下归一化平均尾流速度：（a）X-Y剖面; （b）X-Z剖面Fig. 10 Normalized average wake velocity at different distances in the optimal configuration: (a) X-Y profile; (b) X-Z profile

图11

Fig. 11

	Figure Option ViewDownloadNew Window
	图11 最差构型不同距离下归一化平均尾流速度：（a）X-Y剖面; （b）X-Z剖面Fig. 11 Normalized mean wake velocity at different distances in the worst configuration: (a) X-Y profile; (b) X-Z profile