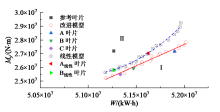引用本文
张祯, 许波峰, 李振, 范星星, 李奎, 汪亚洲. 基于非线性气弹模型的风力机长柔性叶片优化方法[J]. 新能源进展, 2024,12(6): 642-648
ZHANG Zhen, XU Bofeng, LI Zhen, FAN Xingxing, LI Kui, WANG Yazhou. Optimization Method of Wind Turbine Long Flexible Blades Based on Nonlinear Aeroelastic Model[J]. ADV NEW RENEWABLE EN, 2024,12(6): 642-648.  
Doi: 10.3969/j.issn.2095-560X.2024.06.003
Permissions
Copyright©2024, 《新能源进展》编辑部
版权所有 © 《新能源进展》编辑部
基于非线性气弹模型的风力机长柔性叶片优化方法
张祯1,2, 许波峰1,2,†, 李振3, 范星星1,2, 李奎4, 汪亚洲2
1.河海大学 新能源学院,江苏 常州 213200
2.河海大学苏州研究院,江苏 苏州 215100
3.浙江省新能源投资集团股份有限公司,杭州 310020
4.德力佳传动科技（江苏）股份有限公司,江苏 无锡 214105
† 通信作者：许波峰,E-mail：xubofeng@hhu.edu.cn

作者简介：张 祯（1999-）,男,硕士研究生,主要从事风力机叶片设计研究。许波峰（1985-）,男,博士,副教授,硕士生导师,主要从事风力机叶片设计与空气动力学研究。

收稿日期: 2024-05-31 修订日期: 2024-07-08
基金项目: 国家海上风力发电工程技术研究中心开放基金项目（HSFD22004）
摘要

当前大型风力机叶片朝着更长更柔的方向发展,其气动、结构综合性能优化对机组降本增效尤为关键。针对长柔性叶片的非线性特点,采用变步长变形差分法对线性欧拉-伯努利梁模型进行了非线性修正,基于修正的非线性结构模型与叶素动量理论耦合建立了一种兼顾仿真精度与效率的非线性气弹模型。以单机年发电量最大和叶根挥舞弯矩最小为优化目标,采用快速非支配排序遗传算法第二版对DTU 10 MW风力机叶片进行气动-结构一体化优化。通过分析得出非线性气弹模型作为评价函数比线性气弹模型作为评价函数的优化结果综合性能更优,在提升年发电量的基础上,叶根挥舞弯矩均有所降低。

关键词: 长柔性叶片; 优化设计; 非线性; 气弹模型; 遗传算法
中图分类号:TK89 文献标识码:A 文章编号:2095-560X（2024）06-0642-07
Optimization Method of Wind Turbine Long Flexible Blades Based on Nonlinear Aeroelastic Model
ZHANG Zhen1,2, XU Bofeng1,2,†, LI Zhen3, FAN Xingxing1,2, LI Kui4, WANG Yazhou2
1. College of Renewable Energy, Hohai University, Changzhou 213200, Jiangsu, China
2. Suzhou Institute of Hohai University, Suzhou 215100, Jiangsu, China
3. Zhejiang New Energy Investment Group Corporation Limited, Hangzhou 310020, China
4. Delijia Transmission Technology (Jiangsu) Co. Ltd., Wuxi 214105, Jiangsu, China
Abstract

Currently, large wind turbine blades are developing towards greater length and flexibility, making the optimization of their comprehensive aerodynamic and structural performance particularly critical for reducing costs and enhancing efficiency. In this paper, the Euler-Bernoulli beam theory is modified using the variable step deformation difference method for the nonlinear characteristics of long flexible blades. A nonlinear aeroelastic model that considers the simulation accuracy and efficiency is established based on the coupling of the corrected nonlinear structural model and the blade element momentum theory. With the optimization objectives of maximizing the annual power generation of a single machine and minimizing the blade root waving moment, the aerodynamic-structural integration optimization of the DTU 10 MW wind turbine blade was carried out using the non-dominated sorting genetic algorithm-II. The optimization objectives are to maximize annual energy production while minimizing the blade root flapping bending moment. The results indicate that the nonlinear aeroelastic model used as the evaluation function has better overall performance than the linear aeroelastic model used as the evaluation function. The former optimization results can increase the annual energy production and reduce the blade root flapping bending moment.

Key words: long flexible blade; optimized design; nonlinearity; aeroelastic model; genetic algorithm
0 引言

风能作为实现“ 双碳” 目标的关键力量, 未来仍具有巨大的发展空间。叶片是风电机组能量转换的关键部件, 为实现风电机组降本增效, 需要对叶片的气动外形与结构铺层参数展开不断的修改优化。采用传统的叶片气动和结构分开设计并相互迭代校核的设计方法, 不仅在工作量上给工程师带来了巨大的挑战, 还不能得到性能最佳的风力机叶片, 各个设计目标之间不能达成最佳平衡, 也会增加风电机组的制造成本。

梁理论和三维有限元方法（finite element method, FEM）分别具有计算效率高和仿真精度好的特点, 因此在进行考虑气弹耦合效应的叶片气动结构一体化设计时多采用这两种方法。王永志等[1]基于叶素动量（blade element momentum, BEM）理论耦合FEM, 以叶片气动和结构性能为约束, 以质量最小为目标, 采用多岛遗传算法对风力机叶片的叶根、盒型梁、前缘梁、尾缘梁、弦长、扭角等参数进行优化设计, 初步提出了复合材料风力机叶片的气动-结构一体化优化设计方法。KESHAVARZZADEH等[2]通过耦合BEM理论和FEM改进了一种考虑来流风不确定性的叶片优化设计方法。THAPA等[3]采用BEM理论耦合FEM的方法, 在叶尖挠度、固有频率等约束条件下, 对叶片的弦长、扭角和材料铺层参数展开了叶片质量最小与年发电量最大的两目标优化。上述FEM方法虽然提高了气弹仿真模型的计算精度, 获得了更加精确的叶片设计结果, 但受限于算法计算速度和集成开发难度, 在工程实践中难以推广。基于梁理论的气弹仿真模型[4]计算速度更快、易于集成开发, 且具有良好的普适性。郑玉巧等[5]基于BEM理论与线性梁理论建立了叶片静气弹耦合分析模型, 并采用遗传算法对叶片弦长、扭角与铺层厚度展开了叶片质量最小的单目标优化, 实现了1.2 MW机型叶片的降本增效设计。郭小峰等[6, 7]提出了叶片预弯型线设计方法, 以GH Bladed气弹仿真模型为核心, 采用MATLAB构建了预弯叶片的气动外形和铺层结构一体化优化设计模型, 并采用粒子群算法优化得到可满足主机不同匹配需求叶片的Pareto最优解集。风力机叶片的大型化使叶片柔度与弹性变形引起的几何非线性不断增强, 气弹耦合分析愈发被重视[8, 9, 10], “ BEM理论 + 线性梁” 已无法满足长柔性叶片气弹仿真精度的需求。“ BEM理论 + 几何精确梁” 能够考虑长柔性叶片结构的非线性特性, 其在气弹仿真建模中的应用已较为成熟[11, 12]。然而, 由于其复杂度且计算速度较慢, 在耦合多目标优化模型的应用仍很少见。

本文针对长柔性叶片的非线性特点, 基于BEM理论与改进的非线性欧拉-伯努利梁模型（modified Euler-Bernoulli beam theory, MEBBT）, 建立一种兼顾仿真精度与效率的气弹模型, 并通过与Open FAST计算结果比对验证该模型的准确性。以单机年发电量最大和叶根挥舞弯矩最小为优化设计目标, 考虑大变形对叶素径向位置的影响, 引入风轮缩放因子, 采用改进的非线性气弹模型作为评价函数, 发展一种适用于超长柔性叶片的气动-结构一体化多目标优化设计方法, 提高大型风电机组柔性叶片降本增效设计水平。

1 气动弹性仿真模型
1.1 考虑非线性的弹性动力学模型

由于风力机叶片的不断增长, 叶片近似于大型柔性构件, 其结构在复杂载荷作用下发生大变形, 呈现出较强的几何非线性特征。因此, 采用一种变步长变形差分法[13]（variable step deformation difference method, VSDDM）对传统的欧拉-伯努利梁进行修正。

大挠度梁的挠曲线基本方程为

(1)

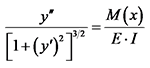式中：y为梁的挠度; x为梁的轴位置; 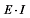为梁的抗弯刚度; M (x)为弯矩。

在满足精度需求的条件下, 式（1）可根据牛顿二项式定理化简为

(2)

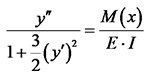在变形差分法中, 通常将梁分为n等分。连带虚拟节点共有n + 2个节点, 节点的序号分别为-1、0、1、2、…、n, 考虑到节点变形在x方向上投影位置的变化, 引入变步长来分析大挠度。步长用h0, h1, …, hi, …, hn表示, 其中h0为虚步长, i表示节点序号, 则：

(3)

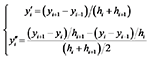将式（3）代入式（2）可得差分形式的大挠度方程：

(4)

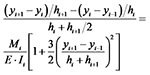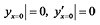
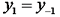
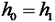
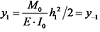
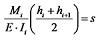
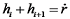
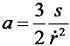
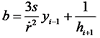
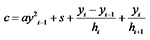
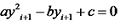
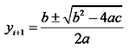结合悬臂梁的边界条件可得： , 由于 , 令 , 则有 。令 ; ; ; ; 。式（4）可化为 , 得到

(5)

1.2 空气动力学计算模型

采用BEM理论作为气动计算模型, 再结合轮毂-叶尖损失因子[14]、Du-S三维旋转效应模型[15]与Glauert修正[16]模型提高其仿真精度、扩展适用范围。

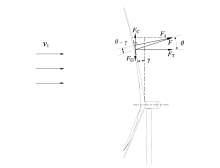
选择方位角0° 的位置对叶片载荷进行计算分析, 如图1所示。

图1 风轮载荷示意图Fig. 1 Schematic diagram of rotor load

叶素上的离心力dFc为：

(6)

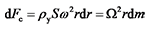式中：ρ y为叶片材料的密度, kg/m3; S为叶素横截面积, m2; dm为该叶素段的质量, kg。

该叶素段所受自身重力dG为：

(7)

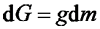式中：g为当地重力加速度, N/kg。

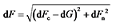
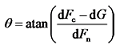
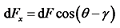
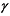
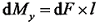
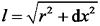
该叶素段所受合力 , Fn由BEM理论计算得到, dF与水平轴线的夹角 。风力机的叶片挥舞载荷 , 其中 为叶片锥角。该叶素段对叶根的挥舞弯矩 , 力臂 , dx为该叶素控制点到变桨轴线的变形量。

由于叶片在发生弹性大变形时叶片形成的扫风面积相对于初始状态有所改变, 仿真计算时的各叶素段径向绝对位置也发生变化。因此考虑叶片的大变形时就必须量化变形后的各叶素段绝对位置, 本文引入了风轮缩放因子Lf。

根据第一型曲线积分[17], 有：

(8)

(9)

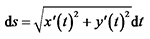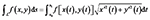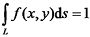
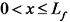
因此通过对叶片的原预弯曲线与变形后的挠曲线进行拟合建立参数化数学模型f (x, y); 曲线L长1.0, 即被积函数 ; , 即x0 = 0, x1= Lf; 可求得风轮缩放因子Lf的数值解。

单台机组年发电量W：

(10)

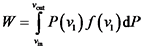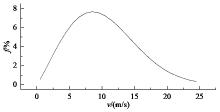
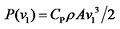
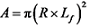
式中：vin为机组切入风速; vout为机组切出风速; P (v1)为来流风速v1下风轮输出功率, ; Cp为风能利用系数; ρ 为空气密度, kg/m3; A为实际扫风面积, ; f (v1)为给定风场Weibull分布风速概率密度函数（见图2）。

图2 风速频率分布Fig. 2 Wind speed frequency distribution

1.3 气弹耦合仿真模型

风力机叶片的气弹耦合仿真计算过程如图3所示。首先, 在叶片无形变的初始条件下, 采用多模型修正BEM理论计算各叶素段的气动载荷。随后, 将气动载荷施加在叶片结构上, 采用MEBBT计算得到各叶素段的变形量, 根据新的变形量重新计算各叶素气动载荷, 将修正后的气动载荷再施加给叶片结构, 求解新的叶片各叶素变形量, 直至叶尖挠度的代差收敛至设定的容许值。

图3 气弹耦合仿真模型Fig. 3 Aeroelastic simulation model

2 长柔性叶片优化设计

风力机叶片的设计涉及气动、结构等多系统的复杂优化问题, 存在众多的设计变量、约束条件和优化目标, 这些因素之间还有复杂的内在耦合关系, 因此在设计时要将其视为一个整体进行考虑。针对多目标优化问题（multi-objective optimization problem, MOP）[18, 19], 发展至今已形成多种能快速有效获得Pareto最优解[20]和解集的算法。Pareto最优状态反映了各目标之间的协调和平衡。多目标遗传算法（genetic algorithm, GA）就是目前被广泛使用的方法之一, 本文采用基于GA的快速非支配排序遗传算法（non-dominated sorting genetic algorithm-II, NSGA-II）[21, 22], 降低了算法的计算复杂度。

2.1 设计变量

叶片参数化建模是借助基本数学几何模型, 使用尽可能少的变量和参数来描述叶片的气动外形与结构特征的方法, 这些变量和参数就是优化设计的变量。气动外形考虑了弦长、扭角、预弯等参数的优化[23], 结构方面则考虑了挥舞刚度[24]。

2.2 约束条件与优化目标

风力机叶片的大挠度变形可能导致叶片与塔筒发生干涉, 因此在叶片设计时必须要约束最小叶片净空以保证风力机的安全运行。根据德国劳氏船级社（Germanischer Lloyd）《风力发电机组认证指南（2010）》的要求, 机组运行时的最小叶片净空Dc, min不得小于叶片未变形时初始净空Dc的30%[25]。

风力机叶片的设计涉及气动、结构等多个方面, 面临众多设计目标[20, 23]。长柔性叶片发生大变形会影响风轮的扫风面积[26], 进而对风轮输出功率和单机年发电量产生不利影响。如果刚度设计过大又会使叶片重量增大, 增加叶根载荷和机组成本。因此, 风力机单机年发电量最大和叶根挥舞弯矩最小之间存在矛盾, 两者需要通过多目标的协调和耦合优化, 以实现综合效益最优。

3 气弹模型验证
3.1 算例介绍

选用DTU 10 MW风力机作为参考算例, 基本参数见表1, 具体参数见文献[27]。

表1 DTU 10 MW风力机基本参数 Table 1 Basic parameters of DTU 10 MW wind turbine
3.2 气弹模型仿真结果

风力机叶片属于悬臂梁结构, 在小变形假设下悬臂梁的任一截面挠度可由线性叠加原理求出。随着风力机叶片的不断增长, 小变形假设条件暴露出了极大的局限性, 叶片挠曲线的仿真结果受到较大影响。考虑到叶片的柔性大变形具有非线性结构特性, 通过建立BEM模型与非线性EBBT模型以多模块接口数据传递技术耦合, 设置叶尖变形挠度值的收敛残差建立非线性气弹模型。为了验证模型的准确性与稳定性, 将非线性气弹模型仿真结果分别与Open FAST平台的AeroDyn + ElastoDyn（BEM耦合线性梁方法, 简称“ AE” ）、AeroDyn + BeamDyn（BEM耦合几何精确梁方法, 简称“ AB” ）气弹模型计算结果进行对比分析, 结果如图4所示。

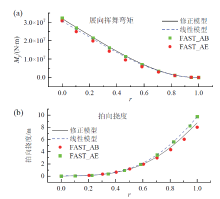图4 额定风速下10 MW风力机叶片的气弹响应Fig. 4 The aeroelastic response of 10 MW wind turbine blades at rated wind speed

由于AB气弹模型基于几何精确梁理论, 考虑了叶片变形所产生的较强的几何非线性, 叶片的挠度变形小于基于线性梁的AE模型, 从而导致叶片锥角大于AE模型, 叶片挥舞载荷大于AE模型。由于叶片刚度由叶根至叶尖不断减小, 使得叶片挥舞弯矩沿展向减小, 叶片的挠度则沿拍向增大。修正前的线性气弹模型与AE模型的仿真结果基本一致, 修正后的非线性气弹模型的挥舞弯矩与AB模型基本一致, 均略大于AE模型, 而叶片挠度介于二者之间, 本文的修正模型结果上更靠近FAST的几何精确梁模型, 表明非线性修正是有效的。

4 优化结果及分析

将建立的气弹仿真模型作为评价函数嵌入NSGA-II, 再引入优化目标、设计约束和设计参数, 即构建了超长柔性叶片气动-结构一体化优化设计平台。综合考虑多目标一体化优化算法的计算效率与优化质量, 优化种群规模为20、优化代数为100, 得到了如图5所示的Pareto最优解集, 其中黑色解集为线性气弹模型作为评价函数的优化结果, 红色解集为非线性气弹模型作为评价函数的优化结果。

图5 两目标优化设计结果Fig. 5 Two-objective optimization design results

图中曲线将优化目标分为I和II两个部分, 第I部分表示在约束条件下无法达到的理想解, 第II部分则表示约束条件下的可行解。最优解集所形成的单调递增特性表明单机年发电量的增加会导致叶根载荷的增大, 机组年发电量最大和叶片叶根挥舞弯矩最小两目标存在不可调和的冲突, 因此, 只能追求综合性能最佳的优化结果。

如图5所示, 参考叶片与优化所得到的Pareto最优解集相比, 其数据点在Pareto最优解集左侧的Ⅱ 区。由两组优化结果的回归分析曲线可知, 采用改进非线性气弹模型作为评价函数优化所得的Pareto最优解集, 较线性气弹模型作为评价函数优化所得的Pareto最优解集更接近 Ⅰ 区的理想解, 即该优化结果叶片综合性能要优于线性气弹模型作为评价函数的结果。

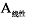
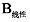
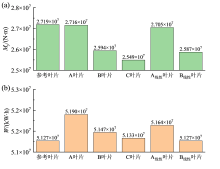
为了更好地解释两目标优化的Pareto最优解集, 在图5中取出了A、B、C、 和 五套性能最优的叶片, 同时采用改进的非线性气弹模型计算叶根挥舞弯矩和单机年发电量, 各叶片计算结果如图6和表2所示。

图6 叶片优化结果对比Fig. 6 Comparison of blade optimization results

表2 优化的A、B、C叶片性能量化分析 Table 2 Quantitative analysis of optimized A, B, and C blade performance

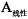
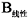
通过比较叶片A与叶片 、叶片B与叶片 , 发现在同等载荷情况下, 非线性优化得到的叶片单机年发电量更大。叶片C相较于叶片 , 尽管载荷较小, 其单机年发电量反而更大。

此外, 与初始叶片相比, 叶片A的单机年发电量最大, 较参考叶片增加了1.24%, 达到5.190 × 107 kW∙ h; 其叶根挥舞弯矩较参考叶片也减小了0.11%, 可能使机组制造成本进一步降低, 从而有效提升了该机组的经济性, 降低了单机度电成本。根据Pareto曲线可以推断, 在保证风力机单机年发电量继续升高的前提下, 通过优化能实现叶根载荷更大的下降, 如B叶片所示。叶片B在单机年发电量增加0.40%的前提条件下, 实现了叶根挥舞减小4.60%的目标, 实现了风力机叶片的降载增效设计, 是满足特定风场风资源条件下10 MW机型的理想叶片设计方案。C叶片在保证单机年发电量不低于参考叶片的前提下, 实现了叶片根部挥舞弯矩6.27%的降载目标, 这为DTU 10 MW风力机进一步降低叶片、传动链、塔架等部件的成本提供了可能。在图5所示的整个最优解集中, 符合预期目标的最优解并不是唯一的, 其他解也展现出比参考叶片更优异的性能。

5 结论

采用多模型修正的BEM气动模型与基于VSDDM的非线性大变形梁结构模型, 建立了适用于超长柔性叶片设计的非线性紧耦合气弹模型。以叶片弦长、扭角、预弯与挥舞刚度等为优化变量, 以机组单机年发电量最大与叶根挥舞弯矩最小为优化目标, 对基准算例DTU 10 MW风力机叶片展开了优化设计, 得出以下结论：

（1）采用变步长变形差分法改进的非线性欧拉-伯努利梁模型在超长柔性叶片气弹仿真中展现出结构非线性特征, 气弹模型仿真计算精度更高且效率较高。

（2）在超长柔性叶片气动结构一体化优化设计中, 将使用非线性气弹模型与使用线性气弹模型的优化结果进行对比, 发现使用非线性气弹模型作为评价函数的优化结果综合性能表现更优。

（3）优化所得的A、B、C三套叶片所适配的风电机组较基准算例都可实现单机年发电量的增加和叶根挥舞弯矩的降低。这为有效降低整机载荷并进一步降低度电成本提供了可行方案。

参考文献
[1] 王永志, 张卫民, 康传明, 等. 复合材料风力机叶片气动/结构一体化优化设计[J]. 太阳能学报, 2012, 33(8): 1301-1306. DOI: DOI:10.19912/j.0254-0096.2012.08.009. [本文引用:1]
[2] KESHAVARZZADEH V, GHANEM R G, TORTORELLI D A. Shape optimization under uncertainty for rotor blades of horizontal axis wind turbines[J]. Computer methods in applied mechanics and engineering, 2019, 354: 271-306. DOI: DOI:10.1016/j.cma.2019.05.015. [本文引用:1]
[3] THAPA M, MISSOUM S. Surrogate-based stochastic optimization of horizontal-axis wind turbine composite blades[J]. Structural and multidisciplinary optimization, 2022, 65(2): 41. DOI: DOI:10.1007/s00158-021-03114-8. [本文引用:1]
[4] 黄可, 张家应, 王青云. 基于非均匀梁模型的二维柔性机翼固有振动分析[J]. 力学学报, 2023, 55(2): 487-496. DOI: DOI:10.6052/0459-1879-22-551. [本文引用:1]
[5] 郑玉巧, 赵荣珍, 刘宏. 大型风力机叶片气动与结构耦合优化设计研究[J]. 太阳能学报, 2015, 36(8): 1812-1817. DOI: DOI:10.3969/j.issn.0254-0096.2015.08.004. [本文引用:1]
[6] 郭小锋, 郭士锐, 杨树峰, 等. 风力机预弯叶片多目标优化设计[J]. 可再生能源, 2017, 35(6): 875-883. DOI: DOI:10.3969/j.issn.1671-5292.2017.06.013. [本文引用:1]
[7] GUO X F, FU X L, SHANG H C, et al. Integrated aero-structural optimization design of pre-bend wind turbine blades[J]. Journal of mechanical science and technology, 2016, 30(11): 5103-5113. DOI: DOI:10.1007/s12206-016-1028-2. [本文引用:1]
[8] DOSE B, RAHIMI H, HERRÁEZ I, et al. Fluid-structure coupled computations of the NREL 5 MW wind turbine by means of CFD[J]. Renewable energy, 2018, 129: 591-605. DOI: DOI:10.1016/j.renene.2018.05.064. [本文引用:1]
[9] LEE K, HUQUE Z, KOMMALAPATI R, et al. Fluid-structure interaction analysis of NREL phase VI wind turbine: aerodynamic force evaluation and structural analysis using FSI analysis[J]. Renewable energy, 2017, 113: 512-531. DOI: DOI:10.1016/j.renene.2017.02.071. [本文引用:1]
[10] WANG L, LIU X W, KOLIOS A. State of the art in the aeroelasticity of wind turbine blades: aeroelastic modelling[J]. Renewable and sustainable energy reviews, 2016, 64: 195-210. DOI: DOI:10.1016/j.rser.2016.06.007. [本文引用:1]
[11] 钱晓航, 郜志腾, 王同光, 等. 百米级大柔性风电叶片非线性气弹响应分析[J]. 空气动力学学报, 2022, 40(4): 220-230. DOI: DOI:10.7638/kqdlxxb-2021.0321. [本文引用:1]
[12] 谢浩, 李德源, 曲珍壮, 等. 基于几何精确梁的风力机叶片动力学建模及动态特性分析[J]. 新能源进展, 2022, 10(3): 203-208. DOI: DOI:10.3969/j.issn.2095-560X.2022.03.003. [本文引用:1]
[13] YUAN G Q, CHEN Y. Geometrical nonlinearity analysis of wind turbine blade subjected to extreme wind loads[C]//Proceedings of the International Symposium on Computational Structural Engineering. Shanghai: Springer, 2009: 521-528. DOI: DOI:10.1007/978-90-481-2822-8_57. [本文引用:1]
[14] 唐新姿, 王效禹, 袁可人, 等. 风速不确定性对风力机气动力影响量化研究[J]. 力学学报, 2020, 52(1): 51-59. DOI: DOI:10.6052/0459-1879-19-214. [本文引用:1]
[15] 许波峰, 王同光, 张震宇. 风力机三维旋转效应模型研究[J]. 太阳能学报, 2014, 35(4): 562-567. DOI: DOI:10.3969/j.issn.0254-0096.2014.04.002. [本文引用:1]
[16] XU B F, WANG T G, YUAN Y, et al. A simplified free vortex wake model of wind turbines for axial steady conditions[J]. Applied sciences, 2018, 8(6): 866. DOI: DOI:10.3390/app8060866. [本文引用:1]
[17] 朱永志, 郑苏娟, 钮群, 等. 高等数学[M]. 南京: 河海大学出版社, 2016: 185. [本文引用:1]
[18] 董新洪, 孙鹏文, 张兰挺, 等. 风力机叶片铺层参数多目标优化设计[J]. 机械工程学报, 2022, 58(4): 165-173. DOI: DOI:10.3901/JME.2022.04.165. [本文引用:1]
[19] 覃锴, 伊鹏辉, 刘兆方, 等. 基于多岛遗传算法的钝尾缘翼型多目标优化设计[J]. 太阳能学报, 2022, 43(9): 218-225. DOI: DOI:10.19912/j.0254-0096.tynxb.2021-0253. [本文引用:1]
[20] 杨阳, 李春, 缪维跑, 等. 基于多目标遗传算法的风力机叶片全局优化设计[J]. 机械工程学报, 2015, 51(14): 192-198. DOI: DOI:10.3901/JME.2015.14.192. [本文引用:2]
[21] CHEN C, WANG L, NIU M H. Research on the application of improved NSGA-II in the structure design of wind turbine blade spar cap[J]. Frontiers in energy research, 2023, 11: 1160423. DOI: DOI:10.3389/fenrg.2023.1160423. [本文引用:1]
[22] WANG L, WANG T G, LUO Y. Improved non- dominated sorting genetic algorithm (NSGA)-II in multi-objective optimization studies of wind turbine blades[J]. Applied mathematics and mechanics, 2011, 32(6): 739-748. DOI: DOI:10.1007/s10483-011-1453-x. [本文引用:1]
[23] 许波峰, 李振, 朱紫璇, 等. 大型下风向柔性叶片参数化建模及两目标优化设计[J]. 太阳能学报, 2023, 44(3): 147-154. DOI: DOI:10.19912/j.0254-0096.tynxb.2021-1247. [本文引用:2]
[24] 廖明夫, 李岩, 王巧艳, 等. 大尺寸风力机叶片流固耦合特性研究[J]. 机械科学与技术, 2018, 37(4): 493-500. DOI: DOI:10.13433/j.cnki.1003-8728.2018.0401. [本文引用:1]
[25] Germanischer Lloyd Industrial Services GmbH. Guideline for the Certification of Wind Turbines[S]. Hamburg: Germanischer Lloyd, 2010. [本文引用:1]
[26] 唐新姿, 何文双, 郭颜威, 等. 顺桨风力机塔叶干涉翼型非稳气动力时频特性[J]. 力学学报, 2023, 55(3): 588-598. DOI: DOI:10.6052/0459-1879-22-554. [本文引用:1]
[27] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Golden: National Renewable Energy Laboratory, 2009. [本文引用:1]