引用本文
王世明, 张少童, 娄嘉奕. 基于CNN-LSTM-ARIMA的超短期风速预测[J]. 新能源进展, 2024,12(6): 688-695
WANG Shiming, ZHANG Shaotong, LOU Jiayi. Ultra-Short-Term Wind Speed Forecasting Based on CNN-LSTM-ARIMA[J]. ADV NEW RENEWABLE EN, 2024,12(6): 688-695.  
Doi: 10.3969/j.issn.2095-560X.2024.06.009
Permissions
Copyright©2024, 《新能源进展》编辑部
版权所有 © 《新能源进展》编辑部
基于CNN-LSTM-ARIMA的超短期风速预测
王世明1, 张少童1, 娄嘉奕2,†
1.上海海洋大学 工程学院,上海 201306
2.苏州市津泰海洋工程研究有限公司,江苏 常熟 215500
† 通信作者：娄嘉奕,E-mail：1301123213@qq.com

作者简介：王世明（1964-）,男,博士,教授,博士生导师,主要从事新能源发电研究。娄嘉奕（1999-）,男,硕士,工程师,主要从事新能源数据分析及预测模型研究。

收稿日期: 2023-09-29 修订日期: 2023-11-10
基金项目: 国家自然科学基金项目（41976194）; 上海市“科技创新行动计划”软科学研究项目（23692102600）; 上海市“科技创新行动计划”上海工程技术研究中心项目（19DZ2254800）
摘要

提升风速预测的精准度对于实时调整电力系统的管理策略及增强风电市场的竞争实力有着关键作用。提出一种基于卷积神经网络（CNN）、长短期记忆网络（LSTM）和自回归集成移动平均（ARIMA）模型的超短期风速预测方法,通过CNN卷积层捕捉时间序列数据中的模式和局部特征,利用LSTM模型对提取的特征进行学习训练,基于CNN-LSTM组合架构模型,预测未来风速并对比实际数据获得残差值,最终利用ARIMA分析历史残差来修正未来的预测误差值,实现对风速的超短期预测。以土耳其某个风电场的实际风速记录为基础,对未来10 min的风速进行预测。结果表明,与CNN-LSTM、双层LSTM传统神经网络模型相比,CNN-LSTM-ARIMA模型对风速预测结果的平均绝对误差分别下降了16.40%、26.92%,能显著提高预测精度。

关键词: 风速预测; 卷积神经网络; 长短期记忆网络; 自回归集成移动平均模型
中图分类号:TK81 文献标识码:A 文章编号:2095-560X（2024）06-0688-08
Ultra-Short-Term Wind Speed Forecasting Based on CNN-LSTM-ARIMA
WANG Shiming1, ZHANG Shaotong1, LOU Jiayi2,†
1. College of Engineering Science and Technology, Shanghai Ocean University, Shanghai 201306, China
2. Suzhou Jintai Ocean Engineering Research Co. Ltd., Changshu 215500, Jiangsu, China
Abstract

Improving wind speed prediction accuracy is important for timely adjustments in power system scheduling plans and enhancing competitiveness in the wind energy market. This paper presents an ultra-short-term wind speed forecasting method based on an ensemble of convolutional neural network (CNN), long short-term memory network (LSTM), and autoregressive integrated moving average (ARIMA). Firstly, CNN convolutional layers capture patterns and local features in time series data. Subsequently, it utilizes LSTM models to learn and train on the extracted features. Based on the CNN-LSTM composite architecture model, it predicts future wind speeds and compares them with actual data to obtain residuals. Finally, it employs ARIMA to analyze historical residuals to correct future prediction errors, achieving ultra-short-term wind speed forecasting. Using measured wind speed data from a wind farm in Turkey as an example, it predicts wind speeds for the next 10 minutes. The results indicate that compared to traditional neural network models like CNN-LSTM and LSTM-LSTM, the CNN-LSTM-ARIMA model has reduced the mean absolute error in wind speed forecasting by 16.40% and 26.92%, respectively, significantly enhancing the prediction accuracy.

Key words: wind speed prediction; convolutional neural networks; long short-term memory network; autoregressive integrated moving average model
0 引言

随着全球对可持续能源需求的不断增加, 越来越多的传统发电设备正在被可再生能源取代。风能是我国“ 十四五” 期间重点发展的主要能源之一, 因其产业日渐进步、发电成本低、绿色环保等优点而受到越来越多的关注[1]。但由于风速的多变特性, 可能影响电网运行的安全性, 不利于风能资源的合理利用[2]。风力发电的功率和稳定性与风速密切相关, 因此, 迅速且准确的风速预测可以为电网调度带来新的思路, 确保电力系统的平稳运转[3]。根据预测时间尺度, 风速预测可分为超短期预测、短期预测、中期预测和长期预测[4]。其中超短期预测主要指预测未来几秒钟到30 min内的风速[5]。准确稳定的超短期风速预测对于调度规划和运行安全具有重要价值。

近年来, 许多研究提出了多种风速预测方法, 可分为4类, 包括物理方法、统计方法、人工智能方法和混合方法[6]。物理方法是基于海拔、地形、温度和湿度等地理和气象信息模拟大气运动过程来预测风速。然而, 物理方法利用一些假设来近似和简化物理模型, 导致预测结果不够准确, 而且还需要额外的背景信息, 计算复杂, 不适合短期和超短期风速预测。统计方法是基于历史数据建立输入数据和输出数据的映射关系。例如, 自回归（autoregressive, AR）模型[7]、自回归滑动平均模型（auto-regressive moving average model, ARMA）[8]和自回归差分移动平均模型（autoregressive integrated moving average model, ARIMA）[9]等, 其特点是结构简单、稳定性高。但在统计方法中, 预测模型是由风速时间序列构建的, 因此限制了其通用性, 预测性能也会随着预测步长的增加而下降[10]。随着人工智能的快速发展, 人工智能方法已被广泛应用于风速预测中, 包括反向传播神经网络（back propagation neural network, BPNN）[11]、递归神经网络（recursive neural network, RNN）[12]和支持向量回归（support vector regression, SVR）[13]等。WANG等[14]总结了各种风速预测方法, 发现基于人工神经网络的风速预测模型通常比其他模型表现更好。与统计方法相比, 人工智能方法在拟合非线性曲线时表现更佳。然而, 人工智能模型的初始权重和阈值是随机生成的, 对预测结果有显著影响。为了克服单个模型的缺点, 实现更准确和稳定的预测值, 混合方法已成为研究热点。混合方法是集成单个预测模型以实现更好的预测值。例如, 将卷积神经网络（convolutional neural networks, CNN）的输出特征输入到长短期记忆网络（long short-term memory, LSTM）中, 以更好地从原始风速数据中提取时空特征[15]。YU等[16]提出了一种改进的小波变换（wavelet transform, WT）与Elman神经网络相结合的方法。SUN等[17]将LSTM、门控循环单元（gated recurrent units, GRU）和深度信念网络相结合, 提高了短期风速预测的性能。当前, 基于深度学习的混合预测模型已成为研究热点。其中, CNN-LSTM混合神经网络模型在垃圾焚烧炉烟气浓度预测[18]、电力负荷预测[19]、PM2.5浓度预测[20]等不同领域中得到了广泛应用。但对于超短期预测, 其为风电场实时调度提供参考, 因此对预测模型的计算效率、精确度提出了更高要求。为了提高CNN-LSTM模型的预测精度, 崔明勇等[21]提出了一种基于密度聚类的完全自适应噪声集合经验模态分解（complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN）和CNN-LSTM的混合模型, 通过密度聚类模态分解增强特征选择来提高短期风电功率预测精度。张培霄等[22]将变分模态分解（variational mode decomposition, VMD）与CNN-LSTM混合模型相结合, 基于VMD分解负荷序列以降低负荷波动性, 有效提高了短期负荷预测的精度。PAN等[23]提出一种基于自注意力机制的CNN-LSTM组合模型, 该模型采用CNN提取油井生产数据的时空特征, 利用LSTM提取油井生产数据的时间序列特征, 利用自注意力机制捕捉输入油井生产数据之间的内在相关性, 实现了更高的油井产量预测精度。

本文基于传统机器学习Boosting算法[24], 创新性提出CNN-LSTM-ARIMA模型来预测超短期风速, 旨在为降低风速预测误差提供新方法和新思路。引入ARIMA以捕捉时间序列数据中的风速波动, 将CNN-LSTM模型的预测值与实际观测值进行比较, 并计算预测值与实际值之间的残差。用ARIMA模型对这些残差进行建模以修正未来CNN-LSTM模型预测的误差, 从而得到更精确的风速预测值。

1 基础理论
1.1 LSTM模型

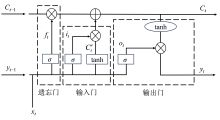
LSTM是对RNN的改进, 是一种可以学习和记忆长期序列信息的递归模型, 解决了长期序列训练中出现的梯度消失和梯度爆炸问题。LSTM模型引入了一种称为“ 门” 的机制, 该机制可以选择性地添加新信息并忘记先前的信息, 从而减少序列长度和网格层数。LSTM结构如图1所示, 主要包括输入门、输出门和遗忘门[25]。

图1 LSTM结构Fig. 1 Structure of LSTM

遗忘门决定t - 1时刻记忆细胞中信息的保留和丢弃, 即给定的信息值可以在内存中保留多长时间以及何时重置记忆单元。输出值介于0~1之间, 输出值接近于1, 保留; 输出值接近于0, 丢弃。相关公式如下：

(1)

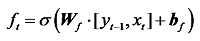式中：ft为遗忘门参数; Wf为遗忘门的权重; yt为隐藏层输出; xt为输入; bf为遗忘门的偏置项。

输入门用于确定哪些新信息可以输入到记忆单元中以更新细胞状态。相关公式如下：

(2)

(3)

(4)

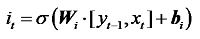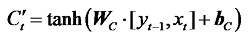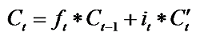式中：it为输入门参数; Wi为输入门的权重; WC为细胞状态的权重; bi为输入门的偏置项; bC为细胞状态的偏置项; 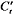为记忆单元的输入状态; tanh为双曲正切函数; Ct为细胞状态。

输出门用于过滤记忆单元中的信息, 并输出最需要的信息, 以预测未来的值。相关公式如下：

(5)

(6)

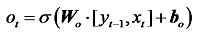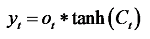式中：ot为输出门参数; σ 为sigmoid函数; Wo为输出门的权重; bo为输出门的偏置项。

1.2 CNN-LSTM模型

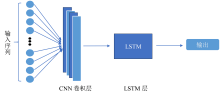
CNN是一种具有强大特征提取能力的前馈深度学习算法[26]。CNN-LSTM模型中, CNN通过卷积操作捕获时间序列数据中的空间特征, 然后将这些特征传递给LSTM, 使LSTM能够进一步对时间依赖性建模。CNN-LSTM混合模型允许模型同时考虑时间和空间信息, 适用于各种时间序列数据分析任务。CNN-LSTM结构如图2所示。

图2 CNN-LSTM结构Fig. 2 Structure of CNN-LSTM

CNN-LSTM具体流程如下。

（1）数据预处理：对数据进行清洗、规范化处理等。

（2）CNN层的应用：CNN层捕获时间序列数据中的空间特征。在CNN层, CNN的卷积操作会在时间序列上滑动卷积核, 从数据中提取特征。CNN通常会有多个卷积核, 每个卷积核用于检测不同的特征。这些卷积核可以是一维卷积核, 沿时间序列轴执行卷积操作。卷积核的大小（窗口大小）和数量是CNN层的关键参数。卷积核的大小决定了其在时间序列上滑动时要覆盖的时间步数量, 从而影响捕获的特征范围。卷积核的数量决定了提取的特征种类。

（3）CNN的输出：通常, CNN的输出会被展平或通过一些操作进行调整, 以匹配LSTM的输入要求。最终, LSTM将CNN的输出作为其时间序列输入。

（4）LSTM的进一步处理：LSTM将CNN的输出作为输入序列, 并在该序列上执行时间依赖性建模, 以捕获额外的时序特征。

1.3 ARIMA模型

ARIMA是一种用于预测和分析时间序列数据的统计模型。ARIMA模型将非平稳时间序列转换为平稳时间序列[27], 然后对因变量的滞后值、随机误差项的当前值和滞后值进行回归, 通过建立时间序列的线性关系来预测未来的值, 用于从单变量时间序列观测中构建时间序列模型。ARIMA模型由以下三部分组成。

（1）自回归（AR）部分：用来建立时间序列数据中的自相关性, 代表了当前值和过去值之间的关系, 根据过去的值以预测未来的值。

(7)

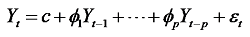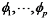
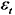
式中：Yt为时间序列的当前值; c为常数项; 为AR模型的参数; p为AR模型的阶数; 为时间t的白噪声误差。

（2）差分（integrated, I）部分：用于处理非平稳时间序列数据, 通过对时间序列数据进行d阶差分操作, 将其转化为平稳时间序列。差分操作是对当前值与前一个值之间的差异进行计算, 从而消除时间序列中的趋势和季节性影响。

（3）移动平均（moving average, MA）部分：负责时间序列数据中的滞后误差项之间的关系, 根据先前预测的误差来预测未来值。

(8)

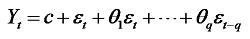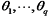
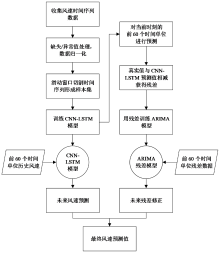
式中： 为MA模型的参数; q为MA模型的阶数。

2 风速预测流程

要预测未来10 min的风速, 需要采用滚动多步预测的方法, 考虑未来10~600 min（10 h）内每10 min的风速。CNN-LSTM-ARIMA模型的预测流程如图3所示。

图3 CNN-LSTM-ARIMA模型流程Fig. 3 Flowchart with CNN-LSTM-ARIMA model

（1）对原始风速数据集进行预处理, 包括数据集中的缺失值、重复值和异常值的清洗以及归一化。

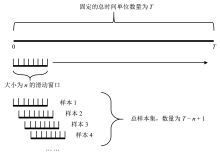
（2）采用滑动窗口对训练数据进行小样本划分。采用61个时间单位（10~610 min）内的风速作为滑动窗口, 如图4所示。选择第一个数据作为起始位置, 然后随着滑动窗口的移动而逐渐向右滑动。将窗口向右滑动一个步长, 即1个时间单位（10 min）的间隔, 然后生成下一个窗口, 并再次提取其中的数据。重复之前的步骤, 直到窗口滑动覆盖了整个时间序列数据集, 即获得多个不重叠的窗口块组成的数据集。

图4 滑动窗口示意图Fig. 4 Rolling window diagram

（3）将滑动窗口分割的时间序列数据用于训练CNN-LSTM模型。61个时间单位组成的样本中前60个时间单位数据作为输入, 最后一个单位的数据作为预测对象, 构建一个CNN-LSTM深度学习模型, 进行多轮次训练, 直到模型损失值不再有明显变化。

（4）将已训练好的CNN-LSTM模型对训练数据集进行预测, 为每个时间单位提供一个预测值, 将预测值与真实值相减得到残差数据。

（5）利用CNN-LSTM模型的残差数据, 训练一个ARIMA模型以捕捉残差的时间依赖性和趋势。基于60个时间单位的残差数据, ARIMA模型可以预测下一个时间点, 提供一个残差修正值。

（6）将CNN-LSTM模型的预测值和ARIMA模型的预测值相加, 得到下一个时间点的综合预测值, 即对风速的最终预测值。

（7）递归应用上述方法, 采用预测目标的前60个时间点的风速数据和残差数据, 代入CNN-LSTM和ARIMA模型, 融合两者预测结果获得目标预测值。每次迭代中, 采用先前时间点的预测值作为输入, 然后更新模型的输入数据并进行下一步预测, 直到预测所需的时间范围结束或者验证样本全部预测完成。

3 算例分析
3.1 数据来源及预处理

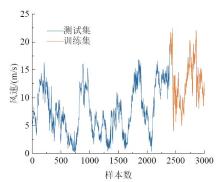
所用数据来自土耳其某风电场的实测数据, 选取时间段为2018年1月1日00:00至2018年1月21日11:30, 其采样间隔为10 min, 共3 000个实验数据。本文所用数据样本足够大, 其风速序列具有周期性和波动性, 能够支持所提模型进行风速预测。实验采用数据的前80%作为训练集, 剩余数据作为测试集。

本文所用数据存在异常风速值, 影响预测性能, 采用相邻数据互补法替换, 风速数据如图5所示。

图5 风速数据Fig. 5 Wind speed data

建立模型前, 为消除不同模型之间的量纲影响, 避免模型训练的复杂化, 采用最大最小归一化方法进行数据预处理, 使得预处理的数据介于0~1之间。

(9)

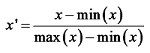式中：x'为归一化后数据; x为归一化前的原始数据; max(x)、min(x)分别为原始数据集的最大值和最小值。

3.2 模型评价标准

为了反映预测值与实际值之间的逼近程度, 采用平均绝对误差（mean absolute error, MAE）、均方根误差（root mean squared error, RMSE）、决定系数R2、平均绝对百分比误差（mean absolute percentage error, MAPE）来评价预测模型能否提高预测精度。其中MAE、RMSE、R2、MAPE的公式分别为：

(10)

(11)

(12)

(13)

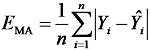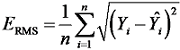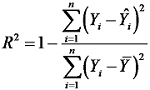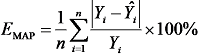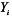
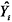
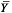
式中：n为样本数量; 为实测风速; 为预测风速; 为实际风速的均值。MAE、MAPE和RMSE越小, 或R2越接近1, 模型的预测性能越好。

3.3 结果分析

为了验证CNN-LSTM-ARIMA模型的精确性和有效性, 将该模型与LSTM模型、CNN-LSTM模型进行对比实验。

实验使用的双层LSTM模型与CNN-LSTM模型架构的不同点在于LSTM模型最上层的LSTM层被替换为CNN层, CNN-LSTM-ARIMA模型与CNN-LSTM模型的底层架构是相同的。实验对每个模型进行100轮的训练, 每次训练会随机使用256个样本。模型参数设置见表1。

表1 模型参数设置 Table 1 Parameters setting for each model

首先, 将归一化的数据代入各模型进行训练, 模型的训练最小样本长度为60, 即使用前60个时间单位的数据对第61个时间单位进行预测, 然后使用rolling window方法来预测未来值并且和验证数据集比较。将长度为600的验证数据进行分段展示, 如图6所示。

图6 不同模型预测效果对比：（a）0~199样本点; （b）200~399样本点; （c）400~599样本点Fig. 6 Prediction comparison of different models: (a) sample points 0 to 199; (b) sample points 200 to 399; (c) sample points 400 to 599

双层LSTM模型在风速起伏不大的情况下表现良好, 如图6（b）所示, 风速缓慢攀升时, 双层LSTM模型捕捉到该上升趋势, 由于LSTM模型具有记忆细胞和门控机制, 能够处理长期依赖关系, 因此对于序列中的渐变趋势能够较好地捕捉, 这使得双层LSTM模型能够对风速序列中的上升趋势做出准确的预测。然而, 如图6（a）所示, 双层LSTM模型在处理风速序列的不稳定振荡方面表现不佳。风速序列通常具有较强的波动性和小型周期性, 而双层LSTM模型可能无法充分捕捉到这些细节。LSTM模型虽然具有记忆机制, 但对于一些快速变化或高频率的波动, 可能会出现短视的情况, 导致预测结果不准确。相比之下, CNN-LSTM模型能够更好地捕捉时间序列的局部和全局信息, 因此无论是趋势还是波动都能兼顾。卷积层能够提取时间序列中的空间结构特征, 而LSTM层则能够对提取的特征进行序列建模, 这使得CNN-LSTM模型在预测风速序列时相对较好。为了弥补上述两个模型在周期性和波动性方面的短视问题, 提出了加入ARIMA模型进行残差修正的方法。ARIMA模型可以捕捉序列的趋势和季节性成分, 通过建立当前值和过去值之间的关系来进行预测, 这样可以提高对风速序列中周期性和波动性的预测能力。ARIMA模型中的AR部分建立了当前值和过去值之间的关系, 可以提供对序列趋势的预测, 而MA部分处理滞后误差项, 进一步提高对风速波动的预测能力。通过引入ARIMA模型, CNN-LSTM-ARIMA混合模型可以综合利用CNN-LSTM模型和ARIMA模型的优势, 从而更好地处理风速序列的趋势、波动和周期性, 能够综合考虑序列的局部和全局信息, 同时通过ARIMA模型对残差进行修正, 提高风速预测准确性。因此, CNN-LSTM-ARIMA混合模型在处理超短期风速预测中具有明显优势。不同模型的预测性能还需要从耗时和精准度来评估。

表2为三种模型的预测性能对比。由结果可知, CNN-LSTM-ARIMA模型的MAE较双层LSTM模型降低34.80%, 较CNN-LSTM模型降低24.51%; MAPE较双层LSTM模型降低26.92%, 较CNN-LSTM模型降16.40%; RMSE较双层LSTM模型降低29.40%, 较CNN-LSTM模型降低16.28%; R2较双层LSTM模型提高19.95%, 较CNN-LSTM模型提高7.62%。提出的CNN-LSTM-ARIMA模型具有最小的MAE、MAPE和RMSE误差, R2最接近1, 应用于超短期风速预测获得了更精确的结果。在训练时间上, 本文所提模型训练时间为76 s, 与CNN-LSTM模型训练时间相当, 但优于双层LSTM模型的178 s。在预测时间上, 双层LSTM模型和CNN-LSTM模型预测时间最短, 均为0.1 s, 但CNN-LSTM-ARIMA模型的预测时长较长（58 s）, 这是由于该模型需要额外对残差进行预测。

表2 不同模型预测性能对比 Table 2 Comparison of prediction performance of different models

综上, 针对预测模型的准确性, CNN-LSTM-ARIMA模型是最佳选择, 具有最低的误差和最高的R2。如果计算资源受限, 且需在短时间内进行实时预测, CNN-LSTM模型可能是更经济的选择。双层LSTM模型在训练时长方面相对较长, 但预测时长非常短, 精准度不如其他两个模型。

4 结论

针对传统神经网络风速时间序列预测模型在复杂多变的风速环境下无法准确预测风速变化、难以学习风速波动等问题, 提出了一种基于CNN-LSTM-ARIMA的风速预测模型, 仿真结果表明：

（1）在风速序列无明显波动时, LSTM、CNN-LSTM、CNN-LSTM-ARIMA的预测结果均拟合良好, 然而一旦风速出现较大波动, CNN-LSTM-ARIMA模型表现更好, 降低了风速的波动性和间歇性为风速预测带来的难度, 具有良好的范化能力, 可以有效捕捉风速的波动变化。

（2）与其他模型相比, CNN-LSTM-ARIMA风速预测模型的平均绝对误差（EMA = 0.045 9）、均方根误差（ERMS = 0.065 8）、平均绝对百分比误差（EMAP = 8.849 3%）最低, 其决定系数最接近1（R2 = 0.858 5）, 预测精度高于其他模型, 验证了所提模型在超短期风速预测方面的正确性和优越性。

（3）虽然所提模型预测精度更高, 但每次进行短期预测时运算时间较长, 成本较高。

在实际运用中, 还可以对模型采取每周更新的方式来应对宏观的季节周期变化导致的风速特性变化, 从而提升预测值的时效性。风速变化的准确预测能及时了解风机出力, 从而采取相应措施减少风电并网对电力运行系统的危害。未来, 若能研究更多优化算法来提高风速预测精度, 将有利于支持新颖的建模和能源模拟技术并提供更安全的全球新能源分配平台。

参考文献
[1] 马海鹏, 王芳, 梁会森, 等. 云南风电项目枯平期发电量占比计算方法探讨[J]. 新能源进展, 2022, 10(6): 573-583. DOI: DOI:10.3969/j.issn.2095-560X.2022.06.011. [本文引用:1]
[2] 李嘉文, 盛德仁, 李蔚, 等. 基于多目标优化和误差修正的短期风速预测[J]. 太阳能学报, 2022, 43(8): 273-280. DOI: DOI:10.19912/j.0254-0096.tynxb.2020-1312. [本文引用:1]
[3] 钱宇, 何益丰, 谢斌鑫, 等. 基于特征工程的XGboost风速短期预测[J]. 武汉大学学报(工学版), 2022, 55(10): 1057-1064. DOI: DOI:10.14188/j.1671-8844.2022-10-011. [本文引用:1]
[4] 赵泽妮, 云斯宁, 贾凌云, 等. 基于统计模型的短期风能预测方法研究进展[J]. 太阳能学报, 2022, 43(11): 224-234. DOI: DOI:10.19912/j.0254-0096.tynxb.2021-0500. [本文引用:1]
[5] LIU H, CHEN C. Data processing strategies in wind energy forecasting models and applications: a comprehensive review[J]. Applied energy, 2019, 249: 392-408. DOI: DOI:10.1016/j.apenergy.2019.04.188. [本文引用:1]
[6] TIAN C S, HAO Y, HU J M. A novel wind speed forecasting system based on hybrid data preprocessing and multi-objective optimization[J]. Applied energy, 2018, 231: 301-319. DOI: DOI:10.1016/j.apenergy.2018.09.012. [本文引用:1]
[7] POGGI P, MUSELLI M, NOTTON G, et al. Forecasting and simulating wind speed in Corsica by using an autoregressive model[J]. Energy conversion and management, 2003, 44(20): 3177-3196. DOI: DOI:10.1016/S0196-8904(03)00108-0. [本文引用:1]
[8] TORRES J L, GARCÍA A, DE BLAS M, et al. Forecast of hourly average wind speed with ARMA models in Navarre (Spain)[J]. Solar energy, 2005, 79(1): 65-77. DOI: DOI:10.1016/j.solener.2004.09.013. [本文引用:1]
[9] 易靖韬, 严欢. 基于小波分解和ARIMA-GRU混合模型的外贸风险预测预警研究[J]. 中国管理科学, 2023, 31(6): 100-110. DOI: DOI:10.16381/j.cnki.issn1003-207x.2021.1174. [本文引用:1]
[10] BRABEC M, CRACIUN A, DUMITRESCU A. Hybrid numerical models for wind speed forecasting[J]. Journal of atmospheric and solar-terrestrial physics, 2021, 220: 105669. DOI: DOI:10.1016/j.jastp.2021.105669. [本文引用:1]
[11] GUO Z H, WU J, LU H Y, et al. A case study on a hybrid wind speed forecasting method using BP neural network[J]. Knowledge-based systems, 2011, 24(7): 1048-1056. DOI: DOI:10.1016/j.knosys.2011.04.019. [本文引用:1]
[12] BARBOUNIS T G, THEOCHARIS J B, ALEXIADIS M C, et al. Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE transactions on energy conversion, 2006, 21(1): 273-284. DOI: DOI:10.1109/TEC.2005.847954. [本文引用:1]
[13] ZHOU J Y, SHI J, LI G. Fine tuning support vector machines for short-term wind speed forecasting[J]. Energy conversion and management, 2011, 52(4): 1990-1998. DOI: DOI:10.1016/j.enconman.2010.11.007. [本文引用:1]
[14] WANG Y, ZOU R M, LIU F, et al. A review of wind speed and wind power forecasting with deep neural networks[J]. Applied energy, 2021, 304: 117766. DOI: DOI:10.1016/j.apenergy.2021.117766. [本文引用:1]
[15] CHEN Y, ZHANG S, ZHANG W Y, et al. Multifactor spatio-temporal correlation model based on a combination of convolutional neural network and long short-term memory neural network for wind speed forecasting[J]. Energy conversion and management, 2019, 185: 783-799. DOI: DOI:10.1016/j.enconman.2019.02.018. [本文引用:1]
[16] YU C J, LI Y L, ZHANG M J. An improved wavelet transform using singular spectrum analysis for wind speed forecasting based on Elman neural network[J]. Energy conversion and management, 2017, 148: 895-904. DOI: DOI:10.1016/j.enconman.2017.05.063. [本文引用:1]
[17] SUN Z X, ZHAO M Y, ZHAO G H. Hybrid model based on VMD decomposition, clustering analysis, long short memory network, ensemble learning and error complementation for short-term wind speed forecasting assisted by Flink platform[J]. Energy, 2022, 261: 125248. DOI: DOI:10.1016/j.energy.2022.125248. [本文引用:1]
[18] 蔡庙辉, 吴昌子, 郇洪江, 等. 基于CNN-LSTM的垃圾焚烧炉烟气浓度预测方法[J/OL]. 化学工业与工程, (2023-10-10)[2023-11-05]. https://doi.org/10.13353/j.issn.1004.9533.20220814. [本文引用:1]
[19] HE W. Load forecasting via deep neural networks[J]. Procedia computer science, 2017, 122: 308-314. DOI: DOI:10.1016/j.procs.2017.11.374. [本文引用:1]
[20] HUANG C J, KUO P H. A deep CNN-LSTM model for particulate matter (PM2. 5) forecasting in smart cities[J]. Sensors, 2018, 18(7): 2220. DOI: DOI:10.3390/s18072220. [本文引用:1]
[21] 崔明勇, 董文韬, 卢志刚. 基于密度聚类模态分解的卷积神经网络和长短期记忆网络短期风电功率预测[J]. 现代电力, 2024, 41(4): 631-641. DOI: DOI:10.19725/j.cnki.1007-2322.2022.0337. [本文引用:1]
[22] 张培霄, 尹晓红, 李少远, 等. 基于VMD-CNN-LSTM的农业大棚园区用电负荷短期预测[J]. 信息与控制, 2024, 53(2): 238-249. DOI: DOI:10.13976/j.cnki.xk.2024.3021. [本文引用:1]
[23] PAN S W, YANG B, WANG S K, et al. Oil well production prediction based on CNN-LSTM model with self-attention mechanism[J]. Energy, 2023, 284: 128701. DOI: DOI:10.1016/j.energy.2023.128701. [本文引用:1]
[24] SCHAPIRE R E. A Brief Introduction to Boosting[C]// Proceedings of the 16th international joint conference on Artificial intelligence. Stockholm: Morgan Kaufmann Publishers Inc. , 1999: 1401-1406. [本文引用:1]
[25] CHEN Y R, WANG Y, DONG Z K, et al. 2-D regional short-term wind speed forecast based on CNN-LSTM deep learning model[J]. Energy conversion and management, 2021, 244: 114451. DOI: DOI:10.1016/j.enconman.2021.114451. [本文引用:1]
[26] 田鹏飞, 于游, 董明, 等. 基于CNN-SVM的高压输电线路故障识别方法[J]. 电力系统保护与控制, 2022, 50(13): 119-125. DOI: DOI:10.19783/j.cnki.pspc.211196. [本文引用:1]
[27] 关涛, 陈普瑞, 于浩. 高拱坝施工仿真参数ARIMA-LSTM时序概率预测方法[J]. 水力发电学报, 2023, 42(11): 146-156. DOI: DOI:10.11660/slfdxb.20231114. [本文引用:1]