开放科学（资源服务）标识码（OSID）： 
0 前言
近些年,椭圆形换热管作为一种强化换热元件日益受到人们的重视[4,5]。与常规圆管换热器相比,椭圆管换热器结构更为紧凑,可以有效减小换热器整体体积,并具有更低的流通阻力和更高的传热效率。目前,关于椭圆形换热器的研究,主要集中在传热和流通性能方面[6,7,8],而对其积灰特性的研究比较少。WALMSLEY 等[9]研究了10种换热管的形式对积灰特性的影响,结果表明椭圆管在抗积灰方面表现出明显的优势。WANG等[10]采用格子玻尔兹曼方法对椭圆形单管的积灰特性进行了数值模拟研究,结果表明,椭圆管的积灰量要明显小于圆管,而且随着椭圆度的增大,积灰量减少。HAN等[11]通过实验研究发现,椭圆管尾部涡流区相对圆管较为狭窄,因此飞灰颗粒进入尾涡区流量减少,飞灰沉积率大大减少。BOURIS等[12]研究表明,相比圆管管束,椭圆管束的沉积率和压降分别下降73%和81%。叶侠丰等[13]对比了圆形管束和椭圆形管束的积灰情况,通过分析流体在换热管附近的低速回流区的大小来研究管束的积灰特性,结果表明,椭圆管束的积灰量明显小于圆管束。由此可见,除了在传热和减阻力方面外,椭圆形换热管在抗积灰方面也有明显作用。但目前的研究较少关注椭圆管的结构和尺寸对飞灰颗粒沉积特性的影响。因此非常有必要进一步开展相关方面的研究,以此加强对椭圆管抗积灰性能的认识。
本文利用计算流体力学（computational fluid dynamics, CFD）商业软件FLUENT对含灰烟气外掠椭圆形换热管的积灰特性进行研究,考察了换热管的椭圆度、烟气流速和颗粒尺寸对飞灰颗粒的沉积特性的影响。该研究可为新型椭圆管换热器的设计和优化提供借鉴。
1 计算模型和方法
1.1 离散相模型
FLUENT软件自带的离散相模型采用欧拉-拉格朗日法的计算思路,以欧拉法来计算流场中的流体相（主相）,以拉格朗日法来计算颗粒相（离散相）。流体中的粒子离散成的一个个粒子,先计算连续相流场,再结合流场变量对每连续相流场中每个颗粒进行受力分析,获得颗粒的速度,从而求得每一个颗粒的轨迹。
在不考虑颗粒间的碰撞和旋转的情况下,认为颗粒主要受曳力、重力和附加力的作用。因此,单个颗粒的运动方程可以写为：
$\frac{\text{d}{{u}_{\text{p}}}}{\text{d}t}={{F}_{\text{D}}}\left( u-{{u}_{\text{p}}} \right)+\frac{g\left( {{\rho }_{\text{p}}}-{{\rho }_{\text{g}}} \right)}{{{\rho }_{\text{p}}}}+F$ (1)
式中：t为时间,s;u为流体的速度,m/s;${{u}_{\text{p}}}$为飞灰颗粒的速度,m/s;${{\rho }_{\text{p}}}$为飞灰颗粒的密度,kg/m3;${{\rho }_{\text{g}}}$为烟气的密度,kg/m3;${{F}_{\text{D}}}\left( u-{{u}_{\text{p}}} \right)$为单个颗粒所受到的曳力,N;$g$为重力加速度,9.81 m/s2;$F$为附加力,N。
在本文的模拟中,只考虑颗粒的曳力、重力、和热泳力的影响,忽略其他附加力的影响。
1.2 沉积模型
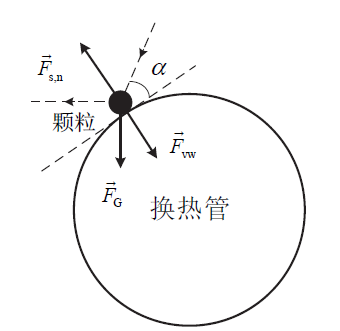
Fig. 1 Sketch of the force analysis on a particle colliding with a heat exchanger tube图1 颗粒撞击换热管时的受力分析简图 |
颗粒所受到的法向弹性反弹力可以表示为：
${{F}_{\text{s,n}}}=Kd_{\text{p}}^{2}\omega _{\text{p}}^{1.2}$ (2)
式中：${{d}_{\text{p}}}$为实际颗粒粒径,m;ωp为颗粒的法向速度,m/s;K的表达式为：
$K\left( {{d}_{\text{p}}} \right)=G{{\left( \frac{{{d}_{\text{p}}}}{{{d}_{\text{ref}}}} \right)}^{n}}$ (3)
式中：$G$为常数,取2;${{d}_{\text{ref}}}$为参考直径,取1 × 10-4 m;n为指数常数,取2.5。
范德华力可以表示为：
${{F}_{\text{vw}}}=\frac{B{{d}_{\text{p}}}}{6{{\delta }^{2}}}$ (4)
式中：$B$为Hanaker常数,取1.0 × 1017 kg∙m2∙s2;$\delta $为颗粒与沉积表面的距离,m。
颗粒所受到的重力可以表示为：
${{F}_{\text{G}}}=\frac{1}{6}\text{ }\!\!\pi\!\!\text{ }d_{\text{p}}^{3}{{\rho }_{\text{p}}}g$ (5)
2 物理模型和计算验证
2.1 模型和计算方法
2.1.1 物理模型及网格划分
采用的二维计算模型如图2所示。计算域的长和宽分别为2 000 mm和400 mm。含灰烟气从左侧进入,从右侧出去。换热管位于计算域的中心。计算区域的边界条件如下：入口采用速度入口边界条件,出口采用压力出口边界条件,换热管壁面采用壁面边界条件,上下边界采用对称边界条件。其中入口的烟气温度为873 K,换热管壁温为723 K。
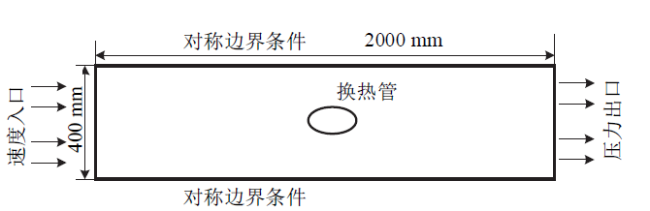
Fig. 2 Schematic diagram of the physical model图2 物理模型的示意图 |
颗粒从左侧以面源的方式喷入计算域中,并设定颗粒入口速度与气相速度相同。颗粒与管束碰撞表面设为反弹边界条件。颗粒的密度为1 692 kg/m3,颗粒的导热系数为0.5 W/(m∙K)。
采用前处理软件Gambit6.3.2对物理模型进行网格划分,采用非结构化网格中的三角形网格。为保证计算精度,采用Gambit自带的Size Function对换热管附近的网格进行加密处理。部分网格划分的示意图,如图3所示。
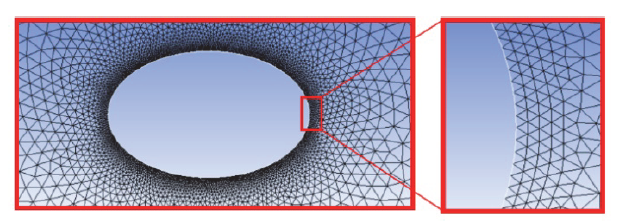
Fig. 3 Schematic diagram of the partial grid division of the computational domain图3 部分网格划分的示意图 |
2.1.2 计算方法
基于稳态数值模拟方法,采用SIMPLEC算法对连续相的压力和速度进行耦合,选择二阶迎风格式对能量控制方程、动量方程和k-ε方程中的对流项进行了离散化。考虑到低雷诺数的影响,湍流模型选择可实现 k-ε模型,壁面采用非平壁函数。辐射模型采用P-1辐射传热模型。在离散型模型中,考虑了离散型和连续相之间的相互影响,进行了双向耦合计算。通过使用随机轨道模型,考虑湍流扩散对颗粒的运动轨迹的影响。
具体的模拟流程如图4所示,首先对连续相流场进行求解,达到完全收敛条件后,投入颗粒,然后耦合求解,直到完全收敛,最后加载用户自定义函数来计算撞击量和沉积量,并将结果输出。
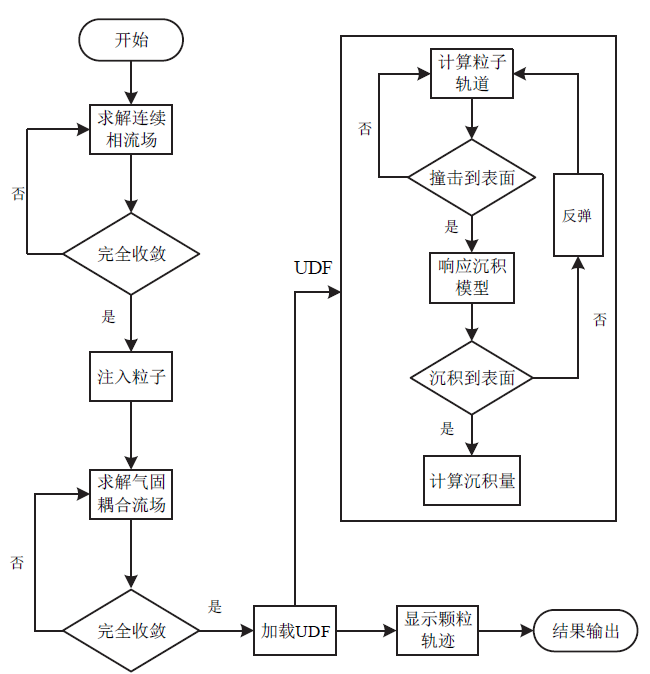
Fig. 4 Flow chart of calculating particle deposition图4 颗粒沉积计算流程 |
2.1.3 相关参数的定义
含灰烟气外掠换热管的示意图如图5所示。其中换热管的椭圆度定义为换热管的长轴与短轴的比值,即a/b。当含灰烟气外掠椭圆形换热管时,飞灰颗粒随烟气一起运动,在换热管附近烟气的运动会受换热管的影响而发生改变,运动惯性较小的颗粒会随烟气一起流动而远离换热管,而运动惯性较大的颗粒会与换热管碰撞,然后反弹或黏附到管壁上。
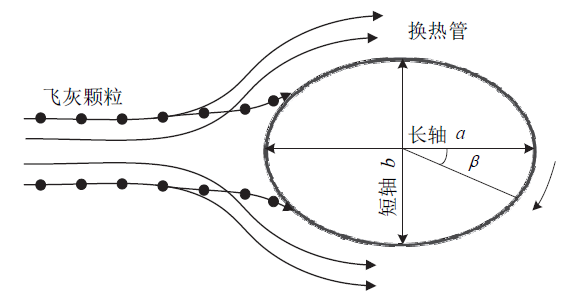
Fig. 5 Schematic diagram of ash-containing flue gas flowing across an elliptical heat exchanger tube图5 含灰烟气外掠椭圆形换热管的示意图 |
为便于分析和比较,引入撞击率、黏附率和沉积率这三个重要的参数,分别定义如下[15]：
$撞击率=\frac{撞击到换热管的颗粒总质量流}{投放到换热管对应的颗粒总质量流}$ (6)
$黏附率=\frac{沉积到换热管的颗粒总质量流}{撞击到换热管的颗粒总质量流}$ (7)
$沉积率=\frac{沉积到换热管的颗粒总质量流}{投放到换热管对应的颗粒总质量流}$ (8)
2.2 计算验证
2.2.1 网格无关性验证
Table 1 Comparisons of the impact efficiencies between the simulated and theoretical values for the cases with different grid nodes表 1 不同网格节点下撞击率模拟值和理论值对比 |
| 网格节点 | 节点尺寸 / mm | 撞击率 | 误差 / % | |
|---|---|---|---|---|
| 理论 | 模拟 | |||
| 24 | 5.236 | 0.108 | 0.075 | 30.6 |
| 48 | 2.618 | 0.108 | 0.101 | 6.5 |
| 96 | 1.309 | 0.108 | 0.115 | 6.5 |
| 192 | 0.654 | 0.108 | 0.098 | 9.3 |
| 384 | 0.327 | 0.108 | 0.110 | 1.9 |
| 768 | 0.164 | 0.108 | 0.106 | 1.9 |
2.2.2 颗粒撞击率验证
颗粒的运动轨道直接影响到颗粒的撞击率。可通过比较数值模拟获得的撞击率与理论计算的撞击率来验证颗粒轨道的可靠性。
颗粒的有效斯托克斯数定义如下[16]：
$St{{k}_{\text{eff}}}=\psi \frac{{{\rho }_{\text{p}}}{{V}_{\text{p}}}d_{\text{p}}^{2}}{9{{\mu }_{\text{g}}}D}$ (9)
式中：${{V}_{\text{p}}}$为颗粒的平均速度,m/s;${{\mu }_{\text{g}}}$为气体的运动黏度,kg·m/s;$D$为换热管直径,m;$\psi $为有效斯托克斯系数,其值与颗粒的雷诺数有关。
颗粒的理论撞击率表达式如下[16]：
${{\eta }_{\text{I}}}\approx {{\left[ \text{1}+b{{\left( St{{k}_{\text{eff}}}-a \right)}^{-\text{1}}}+c{{\left( St{{k}_{\text{eff}}}-d \right)}^{-3}} \right]}^{-1}}$ (10)
式中：a取0.125;b取1.25;c取0.014;d取5.08 × 10-5。
颗粒撞击率的模拟计算值与理论计算值的对比结果如表2所示。从表中可以看出,随着颗粒直径的增大,颗粒在换热管表面的撞击率在增大,而撞击率模拟值与理论值的误差逐渐减小,而且误差在允许范围内,这说明数值模拟颗粒在换热管上的撞击量是合理的。
Table 2 Comparison between the simulated and theoretical values of particle impact efficiencies表2 颗粒的撞击率的模拟计算值与理论计算值的对比 |
| 颗粒粒径 / μm | 撞击率 | 误差 / % | |
|---|---|---|---|
| 理论 | 模拟 | ||
| 3 | 0.097 | 0.093 | 3.85 |
| 5 | 0.329 | 0.316 | 3.91 |
| 10 | 0.696 | 0.708 | 1.76 |
| 15 | 0.840 | 0.835 | 0.69 |
| 20 | 0.905 | 0.917 | 1.38 |
| 30 | 0.955 | 0.954 | 0.15 |
| 35 | 0.967 | 0.969 | 0.21 |
2.2.3 飞灰沉积率验证
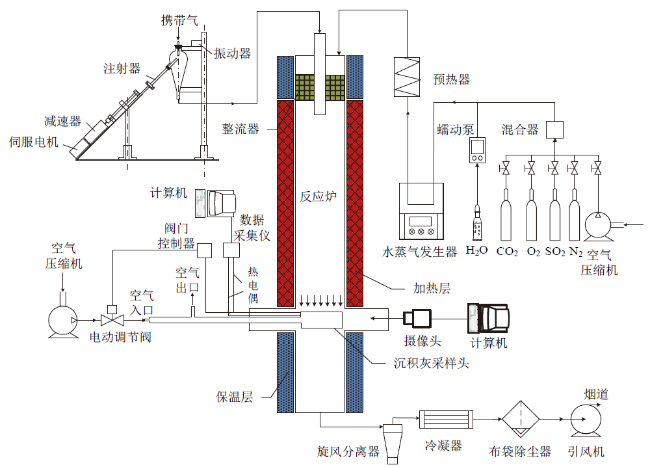
Fig. 6 System diagram of the thermal fly ash deposition test rig图6 热态飞灰沉积试验装置系统图 |
Table 3 Comparison between the simulation results and experimental results表3 模拟结果与实验结果的对比 |
| 入口速度 / (m/s) | 沉积效率 / % | 误差 / % | |
|---|---|---|---|
| 模拟 | 实验 | ||
| 1.14 | 9.44 | 8.64 | 8.47 |
| 1.57 | 8.10 | 7.80 | 3.70 |
| 2.00 | 5.45 | 5.34 | 2.02 |
3 结果与讨论
3.1 换热管椭圆度的影响
对短轴为40 mm,椭圆度分别为1.0、1.2、1.4、1.6、1.8和2.0的椭圆管进行数值模拟,研究了不同椭圆度对不同飞灰颗粒的撞击率、黏附率和沉积率的影响,结果如图7所示。此时,入口烟气速度为5 m/s,颗粒粒径范围为5 ~ 100 μm。
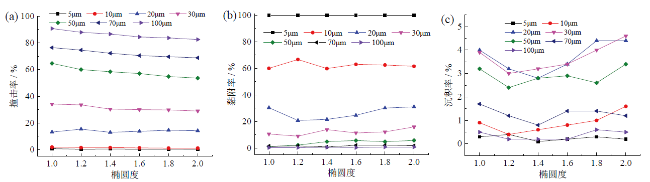
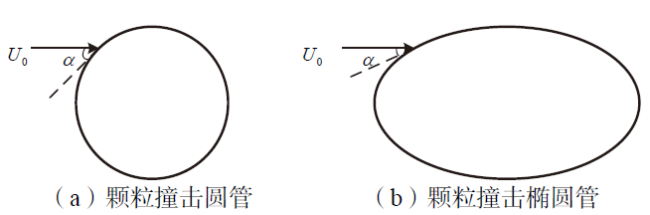
Fig. 7 Simulation results for the cases with different ellipticities: (a) impact efficiency; (b) sticking efficiency; (c) deposition efficiency图7 不同椭圆度下的模拟结果：（a）撞击率;（b）黏附率;（c）沉积率 |
从图7a中可以看出,随椭圆度的增大,10 μm以下颗粒的撞击率并没有显著的变化,但10 μm以上颗粒的撞击率总体上均呈现下降的趋势,而且随着颗粒直径的增大,这种下降的趋势更加明显。从图7b中可以发现,对于直径为5 μm和100 μm的颗粒,随着椭圆度的增大,其黏附率几乎没有变化,而对10 ~ 70 μm的颗粒,其黏附率受换热管椭圆度的影响比较明显,并随椭圆度的增大呈现微小波动的趋势。不同椭圆度下不同颗粒的沉积率如图7c所示。从图中可以看出,随着换热管椭圆度的增大,不同直径的颗粒的沉积率所呈现的规律并不一致。对于5 μm和100 μm的颗粒,椭圆度的变化对其沉积率的影响并不明显。而对于20 ~ 70 μm的颗粒,随着椭圆度的增大,颗粒的沉积率呈现不同的规律。对于50 μm颗粒,其沉积率的变化曲线呈现W形,而其他颗粒的变化曲线大体上呈现V形。另外,最小的沉积率对应的椭圆度大体分布在1.2 ~ 1.6之间。
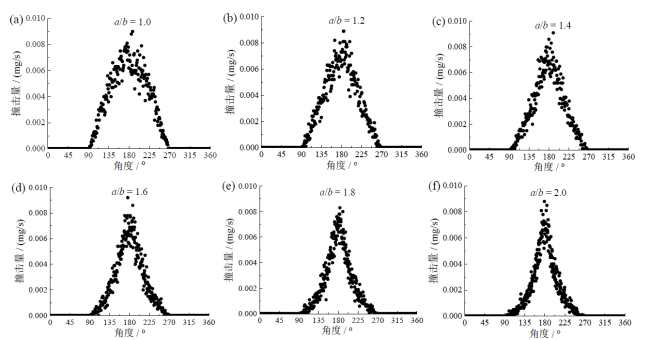
Fig. 8 Distribution of particle impact locations for the cases at different ellipticities图8 不同椭圆度下的颗粒撞击位置分布图 |
为了进一步解释椭圆度对颗粒沉积的影响,分析了颗粒撞击换热管的过程,如图9所示。当颗粒以速度U0撞向换热管时,其法向速度为${{U}_{0}}\cdot \sin \alpha $,而切向速度为${{U}_{0}}\cdot \cos \alpha $。随着椭圆管椭圆度的增大,一方面,撞击角α在减小,意味着气体的切向速度增大,颗粒更容易被气体携带而远离换热管,导致颗粒的撞击率会有所降低。另外一方面,颗粒的法向速度也随之减少,相应地,其法向反弹力会降低,从而导致颗粒易黏附到换热管表面。但是,影响颗粒沉积率的因素更加复杂,与颗粒的直径、烟气的速度和椭圆管的直径均有关系。因此,椭圆度对颗粒沉积率的影响需根据具体情况而定。
Fig. 9 Analysis on the impact process of one particle upon a heat exchanger tube图9 颗粒撞击换热管的过程分析图 |
Fig. 10 Velocity clouds of fluid around the heat exchanger tube for the cases with different ellipticities图10 不同椭圆度下换热管附近流体的速度云图 |
3.2 烟气流速的影响
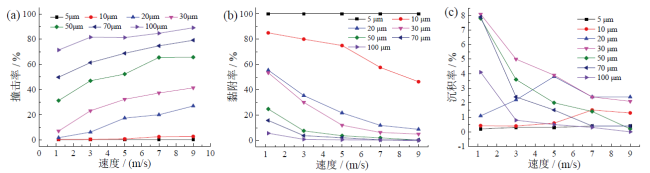
Fig. 11 Simulation results of the cases at different flue gas velocities: (a) impact efficiency; (b) sticking efficiency; (c) deposition efficiency图11 颗粒在不同烟气流速下的模拟结果：（a）撞击率;（b）黏附率;（c）沉积率 |
对于30 ~ 150 μm的颗粒,随着烟气流速的增大,颗粒的沉积率呈明显下降趋势。由此可见,烟气流速对颗粒沉积特性的影响与颗粒的直径有很大关系。对于30 μm以上的大颗粒,随着烟气流速的增大,颗粒的撞击率增大,但黏附率下降,最终沉积率呈下降趋势。
3.3 颗粒粒径的影响
以椭圆度为1.4的椭圆换热管为例,进一步考察了不同直径的颗粒在不同速度下的撞击率、黏附率和沉积率,结果如图12所示。从图12a中可以发现,在粒径5 ~ 150 μm范围内,随着颗粒粒径的增大,颗粒的撞击率不断增大。5 μm颗粒的撞击率趋于0,150 μm颗粒的撞击率接近100%。这是由于小颗粒受气体曳力的影响比较大,不容易撞击到换热管[20],而大颗粒惯性力比较大,容易撞击到换热管上。从图12b可以看出,随着颗粒粒径的增大,颗粒的黏附率急剧下降。由前面沉积模型的表达式可知,颗粒的法向反弹力与颗粒直径的平方成正比。这意味着颗粒直径越大,颗粒的法向反弹力越大,颗粒越容易反弹。图12c表明,在烟气流速为1.14 ~ 9 m/s范围内,随着颗粒直径的增大,5 ~ 150 μm颗粒的沉积率均呈先增大后减小的趋势。在烟气流速为3 ~ 9 m/s范围内,颗粒沉积率的峰值出现在粒径为20 ~ 30 μm之间。
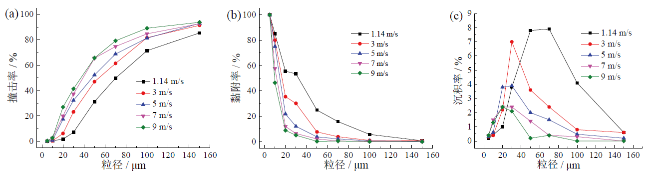
Fig. 12 Simulation results of the cases at different particle diameters: (a) impact efficiency; (b) sticking efficiency; (c) deposition efficiency图12 在不同颗粒直径下的模拟结果：（a）撞击率;（b）黏附率;（c）沉积率 |
图13是椭圆度为1.4、烟气流速为5 m/s条件下,不同粒径颗粒的运动轨迹图。从图中可以看出,随着颗粒粒径的增大,撞击换热管的颗粒数量明显增加。这与前面的模拟结果保持一致。小颗粒气流的跟随性比较好,而大颗粒由于惯性力作用容易撞击到换热管上。
Fig. 13 Trajectories of the particles with different particle sizes图13 不同粒径颗粒的运动轨迹图 |
4 结论
基于ANSYS FLUENT平台,采用用户自定义函数编写相应代码,运用数值模拟的方法对含灰烟气外掠椭圆形换热管的沉积特性进行研究,分别考察了换热管椭圆度、烟气流速以及颗粒粒径三种因素对颗粒的碰撞率、黏附率和沉积率的影响,得到如下结论：
（1）在5 m/s烟气流速下,对于5 μm和100 μm的颗粒,椭圆度的变化对颗粒的沉积率影响不明显,对于20 ~ 70 μm的颗粒,随着椭圆度的增大,颗粒的沉积率呈现不同的规律,但沉积率的最小值大体分布在椭圆度为1.2 ~ 1.6之间;
（2）当烟气流速在1.14 ~ 9 m/s变化,对于30 μm以下的颗粒,其沉积特性的变化规律并不一致,但对30 μm以上的颗粒,随着烟气流速的增大,颗粒的撞击率增大,但黏附率下降,最终沉积率呈下降趋势;
（3）当换热管的椭圆度为1.4,烟气流速控制在1.14 ~ 9 m/s变化时,随着颗粒直径的增大,颗粒的撞击率增大,黏附率下降,沉积率总体上呈现先增大后减小的变化规律,而且当烟气流速大于3 m/s时,颗粒沉积率的峰值出现在粒径为20 ~ 30 μm 之间。
