0 引言
声学法对堆积物料进行测温的应用对象主要是粮食和生物质。YAN等[2]采用实验标定法确定了粮食中声速和温度的物理关系,结合层析成像技术对温度场进行重建,验证了粮食声学法测温的可行性。GUO等[3]采用相同的方法对堆积木质颗粒的单路径声学测温进行了实验验证。此外,HU等[4]直接使用Miki模型探究生物质颗粒粒径等参数对声速的影响。然而,Miki模型只适用于分析孔隙率和曲折度非常接近1的多孔材料。对于孔隙率远小于1的木质颗粒,必须同时考虑流阻、孔隙率和曲折度三个参数对其声学特性的影响[5]。因此,Pàde近似模型（四参数模型）[6]、Johnson-Champoux-Allard（JCA）模型（五参数模型）[7,8]更适合分析堆积木质颗粒的声学特性。
多孔介质声学模型中的参数可以通过实验和参数反演来确定。实验法操作复杂,价格昂贵,很难实现高精度测量。参数反演只需通过一套实验装置测量多孔介质的声学特性指标如声表面阻抗,就可快速确定多孔材料的声学特征参数。BONFIGLIO等[9]对十种不同的多孔材料进行实验研究,通过理论分析探究了参数反演法计算结果的精度和可靠性。这些研究都集中在纤维型和泡沫型的多孔材料,关于尺寸较大的多孔材料如生物质颗粒的研究很少。
目前堆积生物质的声学测温模型是通过实验标定,不能用来分析生物质特性如孔隙率对温度测量的影响,而Miki模型是对纤维类吸声材料声学特性的描述,也不适用于木质颗粒。针对上述问题,有必要建立木质颗粒的声学模型,进而探究堆积木质颗粒中的声速机理。因此,本文采用阻抗管测量木质颗粒在低频声波垂直入射时的声表面特性阻抗和吸声系数,采用参数反演方法建立木质颗粒的JCA模型和Pàde近似模型,并基于JCA模型和Pàde近似模型探究木质颗粒中的声速特性。
1 物理参数反演方法
多孔材料的声表面阻抗Zs(ω)、吸声系数αn(ω)和复阻抗Zc(ω)、复波数kc(ω)存在如下关系[5]：
${{Z}_{\text{s}}}\left( \omega \right)=-j{{Z}_{\text{c}}}\left( \omega \right)\cot \left[ {{k}_{\text{c}}}\left( \omega \right)d \right]$ (1)
${{\alpha }_{\text{n}}}\left( \omega \right)=1-\left| \frac{{{Z}_{\text{s}}}\left( \omega \right)-{{\rho }_{0}}{{c}_{0}}}{{{Z}_{\text{s}}}\left( \omega \right)+{{\rho }_{0}}{{c}_{0}}} \right|$ (2)
式中：d是多孔材料的厚度,m;ρ0是空气密度,kg/m3;c0是自由空间里空气中的声速,m/s。
物理参数反演过程：首先计算JCA模型和Pàde近似模型不同频率下含待求参数的复阻抗和复波数,然后通过式（1）和式（2）分别计算声表面阻抗和吸声系数的模型值Zs,model、αn,model;阻抗管法获得生物质颗粒在声波垂直入射时的声表面阻抗和吸声系数的测量值Zs,meas、αn,meas;根据式（3）或式（4）计算代价函数（cost function, CF）[9],最后选择合适的优化算法计算代价函数最小值,从而确定模型中的物理参数。
$CF\left\{ \left| {{Z}_{\text{s}}} \right| \right\}=\sum\limits_{\omega }{\left| \left| {{Z}_{\text{s,meas}}}\left( \omega \right) \right|-\left| {{Z}_{\text{s,model}}}\left( \omega \right) \right| \right|}$ (3)
$CF\left\{ \left| {{\alpha }_{\text{n}}} \right| \right\}=\sum\limits_{\omega }{\left| {{\alpha }_{\text{n,mear}}}\left( \omega \right)-{{\alpha }_{\text{n,model}}}\left( \omega \right) \right|}$ (4)
1.1 JCA模型
$\rho \left( \omega \right)=\frac{{{\alpha }_{\infty }}{{\rho }_{0}}}{\varphi }\left( 1-j\frac{\sigma \varphi }{\omega {{\alpha }_{\infty }}{{\rho }_{0}}}\sqrt{1+j\frac{4\alpha _{\infty }^{2}\eta {{\rho }_{0}}\omega }{{{\sigma }^{2}}{{\Lambda }^{2}}{{\varphi }^{2}}}} \right)$ (5)
$K\left( \omega \right)=\frac{{\gamma {{P}_{0}}}/{\varphi }\;}{\gamma -\left( \gamma -1 \right){{\left( 1-j\frac{8\eta }{{{\rho }_{0}}\omega {{N}_{\Pr }}{{{{\Lambda }'}}^{2}}}\sqrt{1+j\frac{{{\rho }_{0}}\omega {{N}_{\Pr }}{{{{\Lambda }'}}^{2}}}{16\eta }} \right)}^{-1}}}$(6)
式中：σ是流阻,Pa∙s/m2;φ是孔隙率;α∞是曲折度;Λ是黏性特征长度,m;Λ' 是热特征长度,m;ω是角频率,rad/s;η是空气的动力黏度,Pa∙s;γ是比热比,空气取γ = 1.4;NPr是普朗特数,空气取NPr = 0.71;P0是环境大气压,Pa。温度在0 ~ 100℃范围内,查阅文献[10]得到不同温度下饱和空气的密度和动力黏度值,对其进行拟合结果如下：
${{\rho }_{\text{0}}}\text{=1}\text{.0743}\times \text{1}{{\text{0}}^{-5}}{{T}^{2}}-4.5\times {{10}^{-3}}T+1.2904$ (7)
$\eta ={{10}^{-6}}\left( 0.046T+17.1977 \right)$ (8)
式中：T是温度,℃。
复阻抗和复波数为：
${{Z}_{\text{c}}}\left( \omega \right)=\sqrt{\rho \left( \omega \right)K\left( \omega \right)}$ (9)
${{k}_{\text{c}}}\left( \omega \right)=\omega \sqrt{{\rho \left( \omega \right)}/{K\left( \omega \right)}\;}$ (10)
1.2 Pàde近似模型
刚性多孔介质的孔隙可以近似为具有固定截面形状的棱柱状孔隙,此时孔隙的孔径接近对数正态分布。多孔材料的动力黏度ρ(ω)和复合可压缩系数C(ω)可表示如下[6]：
$\rho \left( \omega \right)=\frac{{{\alpha }_{\infty }}}{\varphi }\left[ {{\rho }_{0}}+j\frac{\sigma \varphi }{\omega {{\alpha }_{\infty }}}F\left( \omega \right) \right]$ (11)
$C\left( \omega \right)=\frac{\varphi }{\gamma {{P}_{0}}}\left[ \gamma -\frac{{{\alpha }_{\infty }}{{\rho }_{0}}\left( \gamma -1 \right)}{\varphi \omega {{N}_{\Pr }}\rho \left( \omega \right)} \right]$ (12)
式中：F(ω)是黏度校正函数。本文中假定堆积生物质孔隙的横截面为圆形,则黏度校正函数的Pàde近似如下[6]：
$F\left( \omega \right)=1+\frac{\frac{\sqrt{2}}{2}{{\text{e}}^{\frac{3}{2}\ln _{2}^{2}\sigma _{\text{s}}^{\text{2}}}}\left( \frac{4}{3}{{\text{e}}^{4\ln _{2}^{2}\sigma _{\text{s}}^{\text{2}}}}-1 \right){{\varepsilon }^{2}}}{\frac{\sqrt{2}}{2}{{\text{e}}^{\frac{3}{2}\ln _{2}^{2}\sigma _{\text{s}}^{\text{2}}}}+\left( \frac{4}{3}{{\text{e}}^{4\ln _{2}^{2}\sigma _{\text{s}}^{\text{2}}}}-1 \right)\varepsilon }$ (13)
$\varepsilon =-j\frac{\omega {{\rho }_{0}}{{\alpha }_{\infty }}}{\sigma \varphi }$ (14)
式中：ε是复合无量纲的参数组合;σs为孔径分布的标准差。
Pàde近似模型中复阻抗和复波数为：
${{Z}_{\text{c}}}\left( \omega \right)=\sqrt{\frac{\rho \left( \omega \right)}{C\left( \omega \right)}}$ (15)
${{k}_{\text{c}}}\left( \omega \right)=\omega \sqrt{\rho \left( \omega \right)C\left( \omega \right)}$ (16)
1.3 最小化算法
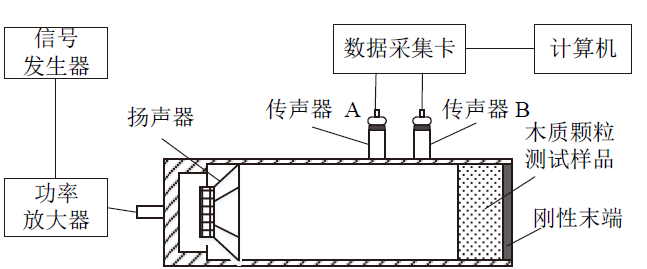
2 实验装置
Fig. 1 Schematic diagram of impedance tube for measuring the surface acoustic impedance and sound absorption coefficient图1 阻抗管法测量木质颗粒的声表面阻抗和吸声系数的硬件示意图 |
单个木质颗粒是圆柱体型的,直径和长度分别为8 mm和10 ~ 35 mm。图2所示为测量样品。颗粒被装在亚克力管内,两端用金属网格固定,其长度和外径均为100 mm,壁厚为2 mm。对三个样品进行测量,取平均值作为测量结果。实验时,环境大气压为101.7 kPa,温度为23℃。
Fig. 2 Test samples of wood pellets图2 木质颗粒测试样品 |
3 结果和分析
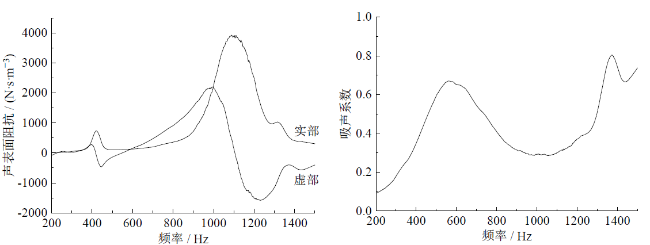
3.1 阻抗管测量结果
木质颗粒在声波垂直入射时的声表面阻抗和吸声系数测量结果如图3所示。声表面阻抗和吸声系数呈现一定的周期性。在实验频段内,声表面阻抗出现两个峰值,与堆积沙石（平均粒径15 ~ 20 mm）的声表面阻抗随频率的变化规律类似[5]。对于纤维型和泡沫型多孔材料,在该频段的声表面阻抗没有出现峰值,实部是接近平行于横轴的直线,虚部是单调递增的[5-6,11]。产生这种差异的原因主要在于圆柱体颗粒的平均粒径大小对流阻、孔隙率等参数的影响。纤维型和泡沫型的多孔材料骨架的平均粒径大概在100 μm数量级,而木质颗粒的平均粒径大概是它们的80倍。平均粒径越大,声表面阻抗的峰值往低频方向偏移,峰值变化周期缩短,因此可以在200 ~ 1 500 Hz频段内观察到两个峰值。吸声系数也表现出类似的变化,这与PEREIRA等[12]对不同粒径黏土颗粒的吸声系数的测量结果一致。
Fig. 3 (a) Measured values of surface acoustic impedance of wood pellets; (b) measured values of sound absorption coefficient of wood pellets图3 （a）木质颗粒的声表面阻抗测量值;（b）木质颗粒的吸声系数测量值 |
3.2 物理参数反演结果
物理参数反演方法确定JCA模型和Pàde近似模型中的物理参数,包括流阻、孔隙率、曲折度、黏性特征长度、热特征长度和孔径分布的标准差,计算结果如表1所示,表中Imp_JCA_NMSM表示基于声表面阻抗的采用NMSM算法进行参数反演确定JCA模型中的参数值,其余同理。从表中可以看到,虽然通过参数反演的方法不能得到物理参数的唯一值,但可以确定物理参数的大概取值范围。相比这些参数的具体取值,通过反演方法计算的木质颗粒的声表面阻抗和吸声系数的模型值和实验值的一致性更重要。
Table 1 Inversion results of physical parameters in JCA model and Pàde approximate model表1 JCA模型和Pàde近似模型中物理参数反演结果 |
| 编号 | 参数设置 | σ / (Pa·s·m-2) | φ | α∞ | Λ / μm | Λ' / μm | σs |
|---|---|---|---|---|---|---|---|
| 1 | Imp_JCA_NMSM | 1 698 | 0.496 | 1.90 | 344 | 385 | - |
| 2 | Imp_JCA_GA | 1 521 | 0.543 | 2.03 | 284 | 577 | - |
| 3 | Imp_Pàde_NMSM | 1 037 | 0.479 | 1.56 | - | - | 0.76 |
| 4 | Imp_Pàde_GA | 1 587 | 0.476 | 1.57 | - | - | 0.52 |
| 5 | Coe_JCA_NMSM | 1 532 | 0.627 | 1.58 | 174 | 301 | - |
| 6 | Coe_JCA_GA | 2 532 | 0.722 | 2.20 | 157 | 510 | - |
| 7 | Coe_Pàde_NMSM | 2 271 | 0.706 | 1.75 | - | - | 0.46 |
| 8 | Coe_Pàde_GA | 2 153 | 0.706 | 1.74 | - | - | 0.49 |
木质颗粒的声表面阻抗和吸声系数的模型值计算结果如图4和图5所示。对于声表面阻抗,木质颗粒的声表面阻抗测量值的实部在频率为400 Hz和1 100 Hz处均出现峰值,整个实验频段内呈现“双峰特性”,但木质颗粒的声表面阻抗模型值只能拟合出1 100 Hz处的峰值。这是由于木质颗粒在400 Hz处声表面阻抗实部测量值只有1 100 Hz处峰值的20%,两个峰值是随频率递增的,而JCA模型和Pàde近似模型计算的声表面阻抗实部的峰值呈现周期性衰减,不能拟合出峰值递增的状态。木质颗粒的吸声系数的模型值和实验值的一致性更好。频率在200 ~ 1 200 Hz范围内,木质颗粒吸声系数的模型值与测量值基本吻合。
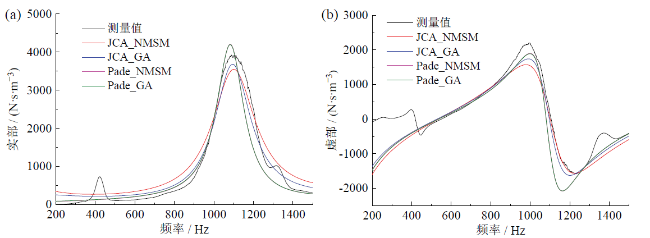
Fig. 4 Predicted values of surface acoustic impedance of wood pellets based on parameter inversion: (a) real part; (b) imaginary part图4 基于参数反演的木质颗粒的声表面阻抗模型值：（a）实部;（b）虚部 |
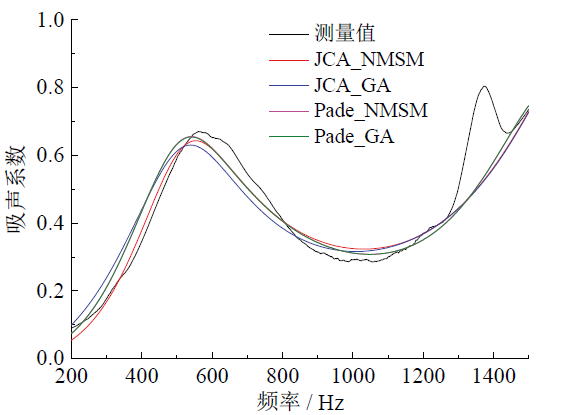
Fig. 5 Predicted values of sound absorption coefficient of wood pellets based on parameter inversion图5 基于参数反演的木质颗粒吸声系数模型值 |
3.3 木质颗粒中声波传播速度
多孔介质复波数的实部和声速存在如下关系：
${{c}_{f}}=\frac{2\text{ }\!\!\pi\!\!\text{ }f}{\operatorname{Re}\left( {{k}_{\text{c}}} \right)}$ (17)
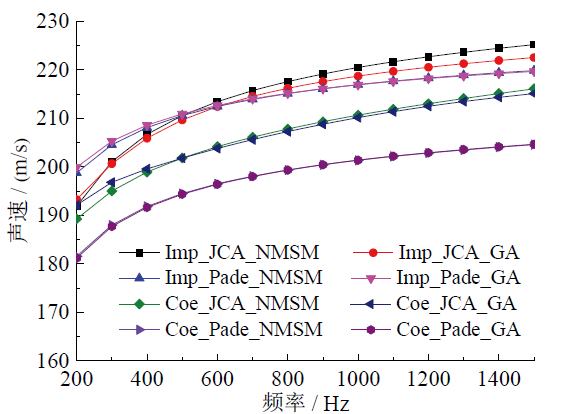
Fig. 6 Theoretical relationship between frequency and sound speed of wood pellets with T = 23oC图6 23℃时不同频率下木质颗粒的声速模型值 |
线性扫频信号是探究声学法测温时最常用的声源信号。在选择线性扫频信号作为声源时,测得声波速度是在实验频段里的平均声波速度。根据式（18）可以计算固定频率范围内的平均声波速度cm：
${{c}_{\text{m}}}=\frac{\int{{{c}_{f}}\text{d}f}}{\int{\text{d}f}}$ (18)
生物质内部因自加热温度超过80℃时,自燃风险达到预警点[1]。因此,应用声学法进行堆积生物质内部温度测量,要求声学法在20 ~ 80℃范围内的测温精度尽可能高。对于JCA模型和Pàde近似模型,由式（5）和式（6）、式（11）和式（12）可知,0 ~ 100℃温度范围内,随温度变化最大的参数是空气密度和空气动力黏度,其他参数随温度变化很小,可视为定值。根据式（7）和式（8）计算20 ~ 80℃的空气密度和空气动力黏度,然后代入JCA模型和Pàde近似模型计算复波数,最后根据式（17）和式（18）计算不同温度下木质颗粒孔隙中的声速,结果如图7所示。在同一温度下,木质颗粒中的声速远小于自由空间空气中的声速,数值约为自由空间中声速的三分之二。当温度发生变化时,自由空间中空气里的声速变化梯度比木质颗粒孔隙中更明显,大约是孔隙中声速的两倍。这个理论温度和声速关系和GUO等[3]和HU等[4]利用线性扫频信号测得的实验结果具有高度一致性。
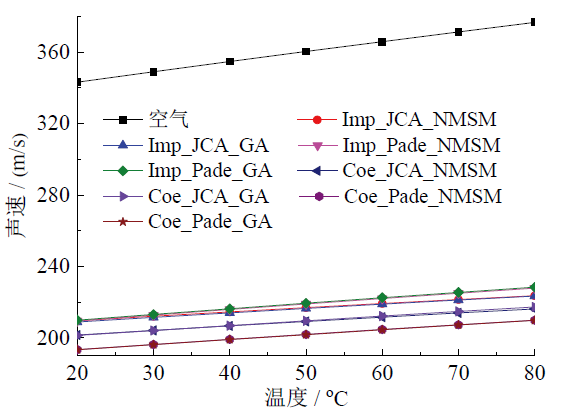
Fig. 7 Theoretical relationship between temperature and average sound speed of wood pellets with the frequency of sound waves (in the range of 200-1500 Hz)图7 200 ~ 1 500 Hz内木质颗粒的平均声速和温度关系 |
4 结论
提出了一种基于木质颗粒的声学特性建立声学测温模型的方法。首先使用阻抗管测量频率范围在200 ~ 1 500 Hz内木质颗粒的声表面阻抗和吸声系数,并且通过参数反演确定模型参数,其中木质颗粒样品的流阻取值范围是1 037 ~ 2 532 Pa∙s/m2,孔隙率取值范围是0.476 ~ 0.722,曲折度取值范围是1.56 ~ 2.22。JCA模型和Pàde近似模型能对木质颗粒的声学特性进行准确描述,验证了基于物理参数反演的多孔介质声学理论对堆积木质颗粒进行声学特性分析的可行性。根据建立的JCA模型和Pàde近似模型,结合空气密度、动力黏度和温度的关系计算得到不同温度下木制颗粒中的声速。室温23℃时,木质颗粒中的声速处于200 ~ 220 m/s范围内,此后随温度的升高,速度的变化梯度只有空气中声速随温度变化的一半,与已有研究的实验结果一致。该声学测温模型能准确地反映堆积木质颗粒中的声速规律。
