0 引言
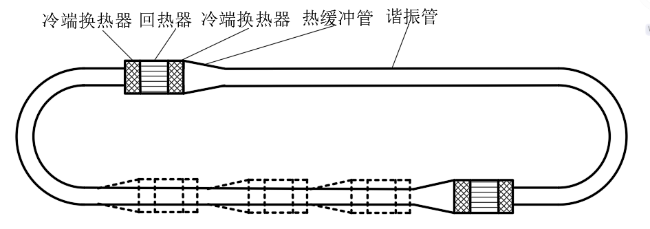
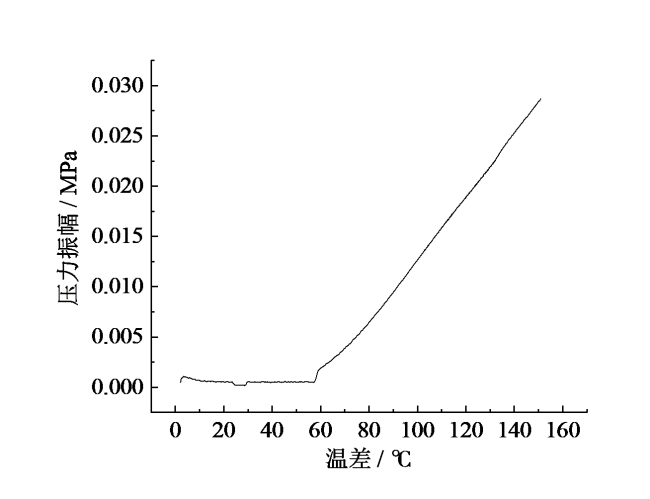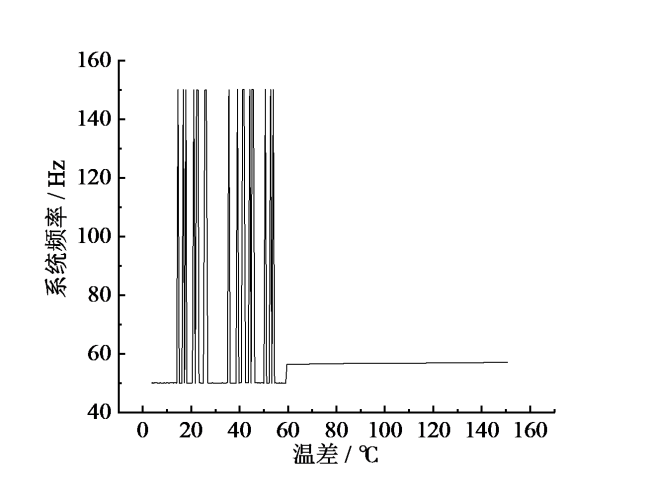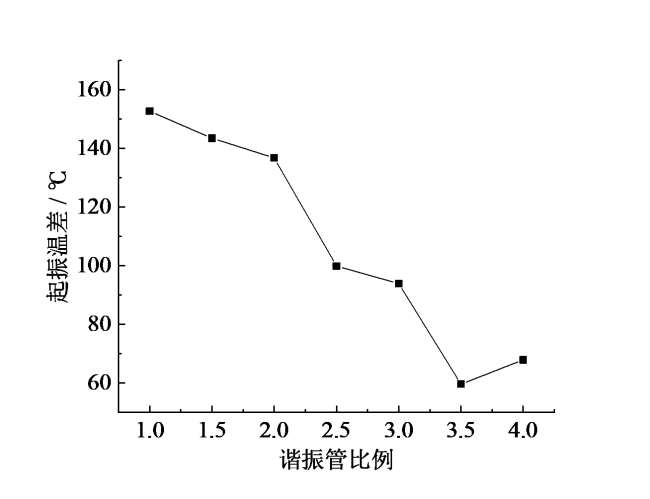利用热声效应[1,2]制造的热声热机具有传统热机无法比拟的优点,如结构简单无运动部件、工质环保无危害、使用寿命长、可利用低品位热源、应用范围广等特点[3,4],具有很好的发展潜力。1979年,CEPERLEY[5]首次提出行波热声热机概念。在行波热声热机中,气体压力波动和体积流率波动的相位差为零且忽略黏性损失,则气体经历了可逆的热力循环,因此,行波热声热机的理想效率可以达到卡诺循环的效率。CERPERLY在之后的研究中发现,为获得较高的热声转换效率,在保证回热器处于行波声场的前提下,还需要增加回热器处的声学阻抗,以减小气体速度过大引起的黏性损失[6,7]。2002年,SWIFT[8]介绍了一种级联式热声发动机,其由一个驻波发动机和两个行波发动机串联组成,大部分声功是在高效行波发动机中产生的,该发动机的热声转换效率为20%,但是通过理论计算该台发动机可以达到卡诺效率的35% ~ 40%。2010年,荷兰Aster热声公司的DE BLOK引入了多级行波热声热机的概念[9,10]并研制出一种包含四个热声热机单元的环路多级行波热声热机,该系统采用了较大横截面积的回热器单元,使得气体的振荡速率有效降低,从而提高了回热器处的声学阻抗,进而降低了气体通过回热器时的黏性损失。研究结果显示,当采用2.1 MPa的氩气作为工质时,系统可在回热器冷热端温差小于30 K的条件下起振。2017年浙江大学的杨睿等系统提出并建造了单级、双级、三级和四级低品位热源驱动的环路热声发动机[11,12],通过实验验证了利用低品位热源驱动的可行性。指出在环路结构的一种典型声场分布里,有四个相距大约1/4波长的纯行波点,这四个点都是安装回热器的潜在理想位置。当以1 MPa的CO2为工质时,三级和四级系统的起振温度可低至29℃（对应的起振温差为17℃）。
目前,大多数关于多级环路行波热声热机的文献基本都是属于热声核处于中心对称位置的相关研究,然而对于热声核位置非对称的研究相对较少,本文将通过理论分析和实验探究阐述双级环路行波热声热机的两个热声核从中心对称位置逐渐靠近时对热声系统的起振温度、谐振频率、压比等相关参数的影响,从而揭示双级环路行波热声热机系统在热声核位置非对称时的相关特性,可为今后多级行波热声热机系统的设计以及理论分析提供一定的指导,并为实际的工程应用奠定基础。
1 实验装置介绍
1.1 双级环路行波热声热机主体介绍
双级环路行波热声热机试验装置实物图如图1所示,该热声热机是由两个热声核和谐振管通过法兰连接成闭合回路,其中热声核是由冷端化热器、回热器、热端化热器以及热缓冲管构成。
Fig. 1 Physical picture of the two-stage traveling wave thermoacoustic engine图 1 双级行波热声发动机实物图 |
Table 1 Dimensions of the components of the two-stage traveling wave thermoacoustic heat engine表 1 双级行波热声热机各部件尺寸 |
| 部件名称 | 内径 / m | 长度 / m | 孔隙率 | 材质 |
|---|---|---|---|---|
| 冷端换热器 | 0.100 | 0.030 | 0.270 | 黄铜 |
| 回热器 | 0.100 | 0.060 | 0.068 | 不锈钢 |
| 热端换热器 | 0.100 | 0.030 | 0.270 | 黄铜 |
| 热缓冲管 | 0.100（直管段） | 0.090 | 1.000 | 不锈钢 |
| 大端0.100,小端0.050（锥形管段） | 0.090 | |||
| 谐振管 | 0.050 | 5.000 | 1.000 | 不锈钢 |
| 气库 | 0.080 | 0.080 | / | 不锈钢 |
图2所示是非对称双级环路行波热声发动机的示意简图,通过不断调整两个热声核单元的相对位置,使其连接两个热声核单元的谐振管长度按比例变化。本文对谐振管比例（连接两个热声核所使用的管道长度比例）分别为1:1、1:1.5、1:2、1:2.5、1:3、1:3.5、1:4进行实验研究。着重对起振温度和压比做了较为详细的说明。
Fig. 2 Schematic diagram of the relative position change of the thermoacoustic nucleus图 2 热声核相对位置变化示意简图 |
1.2 压力与温度测量
1.2.1 温度测量
在热声系统中通过在热声核的热端换热器和冷端换热器分别放置K型热电偶来测量热端温度和冷端温度。把热电偶所采集到的电信号接入到NI-9214温度采集卡中,然后将数据传输到LABVIEW软件中进行处理。
1.2.2 压力测量
在本热声系统中设置4个压力采集点,采用GE公司的动态压力传感器进行测量,其量程范围为0 ~ 5 MPa。将压力传感器所采集的电信号传输到压力采集卡中,然后将数据传输到LABVIEW软件中进行分析。
2 理论基础
2.1 热力学基础
从热力学的角度揭示热能与声能的转化机理,理想气体的多变过程关系式为[2]：
$\frac{{{T}^{n}}}{{{p}^{n-1}}}=C$ (1)
式中：T为温度;P为压力;n为多变指数;C为常数。对式（1）求导可得
$\frac{\text{d}T}{T}=\frac{n-1}{n}\frac{\text{d}p}{p}$ (2)
从式（2）可知,在多变过程中（除n = 1为等温过程,n = 0为等压过程）,当温度变化时压力必然也会发生相应的变化;同样,当压力变化时温度也会发生相应的变化。这也是热声效应能发生的热力学基础。
2.2 线性热声理论
基于可压缩黏性流体在连续介质的假设,热声系统中的流体在流动时需满足以下基本控制方程[2]。
连续性方程：
$\frac{\partial \rho }{\partial t}+\nabla \left( \rho u \right)=0$ (3)
动量方程：
$\rho \left( \frac{\partial u}{\partial t} \right)+\rho \left( \nabla u \right)u=-\nabla p+\mu {{\nabla }^{2}}u+\rho f$ (4)
能量方程：
$\begin{align} & \rho {{c}_{p}}\left( \frac{\partial T}{\partial t}+u\nabla T \right)=\beta T\left( \frac{\partial p}{\partial t}+u\nabla p \right)+ \\ & \nabla \left( k\nabla T \right)+\text{ }\!\!\Phi\!\!\text{ } \end{align}$ (5)
状态方程：
$\rho =\rho \left( T,p \right)$ (6)
式中：p为流体的压力;u为速度;ρ为密度;T为温度;${{c}_{p}}$为定压比热容;k为热导率;β为热膨胀系数;μ为动力黏度;f为体积力;$\text{ }\!\!\Phi\!\!\text{ }$为耗散项;t为时间。
为求解以上基本控制方程,基于以下假设对其进行频域内线性化处理：①固体介质为刚性材料;②运动工质为理想气体,不考虑径向的流体参数;③声场为小振幅振荡,振荡波为正弦形式;④流体热穿透深度、黏性穿透深度和系统各部件的径向尺寸远小于波长。
基于上述假设,基本控制方程的求解可用复数形式表达,以下波动量用复数表示为：
$p\left( x,t \right)={{p}_{\text{m}}}\left( x \right)+Re\left[ {{p}_{1}}\left( x \right){{\text{e}}^{i\omega t}} \right]$ (7)
$\rho \left( x,y,z,t \right)={{\rho }_{\text{m}}}\left( x \right)+Re\left[ {{\rho }_{1}}\left( x,y,z \right){{\text{e}}^{i\omega t}} \right]$ (8)
$T\left( x,y,z,t \right)={{T}_{\text{m}}}\left( x \right)+Re\left[ {{T}_{1}}\left( x,y,z \right){{\text{e}}^{i\omega t}} \right]$ (9)
$u\left( x,y,z,t \right)=Re\left[ {{u}_{1}}\left( x,y,z \right){{\text{e}}^{i\omega t}} \right]$ (10)
式中：ω为角频率;i为复数中的虚数单位;下标1为参数的一阶波动量;下标m为该参数的平均值。将式（7）~ 式（10）代入到式（3）~ 式（5）中,进行积分转换可以得到压力梯度方程、温度波动方程、速度梯度方程。
压力梯度方程：
$\frac{\text{d}{{p}_{1}}}{\text{d}x}=-\frac{i\omega {{\rho }_{\text{m}}}}{1-{{f}_{\mu }}}\frac{{{U}_{1}}}{A}$ (11)
式中：${{f}_{\mu }}$为黏性分布函数的截面平均积分函数;U1为截面平均体积流率。
温度波动方程：
$\begin{align} & {{T}_{1}}~~=\frac{1}{{{\rho }_{\text{m}}}{{c}_{p}}}\left( 1-{{h}_{k}} \right){{p}_{1}}- \\ & \frac{1}{i\omega A}\frac{\text{d}{{T}_{\text{m}}}}{\text{d}x}\frac{\left( 1-{{f}_{k}} \right)-\sigma \left( 1-{{h}_{\mu }} \right)}{\left( 1-{{f}_{\mu }} \right)\left( 1-\sigma \right)}{{U}_{1}} \end{align}$ (12)
式中：${{h}_{k}}$为热弛豫分布函数;${{f}_{k}}$为热弛豫分布函数的截面积分函数;hμ为黏性分布函数;$~\sigma $为普朗特数。
速度梯度方程：
$\begin{align} & \frac{\text{d}{{U}_{1}}}{\text{d}x}=-\frac{i\omega A}{\gamma {{p}_{\text{m}}}}\left[ 1+\left( \gamma +1 \right){{f}_{k}} \right]{{p}_{1}}+ \\ & \frac{\left( {{f}_{k}}-{{f}_{\mu }} \right)}{\left( 1-{{f}_{\mu }} \right)\left( 1-\sigma \right)}\frac{\text{d}{{T}_{\text{m}}}}{\text{d}x}\frac{{{U}_{1}}}{{{T}_{\text{m}}}} \end{align}$ (13)
式（12）和式（13）分别为线性热声理论的两大控制方程,即动量方程、连续性方程。这两个方程是分析热声现象的有力工具。
2.3 热声能量流理论
热声系统中的能量流分为声功流和总能流[2]。
2.3.1 声功流
声功流是表征单位时间内声波传播方向上截面平均的声功,其表达式如下：
$\begin{align} & {{{\dot{E}}}_{2}}\left( x \right)=\frac{\omega }{2\text{ }\!\!\pi\!\!\text{ }}\int Re\left[ {{p}_{1}}\left( x \right){{\text{e}}^{i\omega t}} \right]Re\left[ {{U}_{1}}\left( x \right){{\text{e}}^{i\omega t}} \right]\text{d}t \\ & =\frac{1}{2}Re\left[ {{p}_{1}}{{{\tilde{U}}}_{1}} \right]=\frac{1}{2}Re\left[ {{{\tilde{p}}}_{1}}{{U}_{1}} \right] \\ & =\frac{1}{2}\left| {{p}_{1}} \right|\left| {{U}_{1}} \right|\cos \theta \end{align}$ (14)
式中：$\left| {{p}_{1}} \right|$为压力振幅;$\left| {{U}_{1}} \right|$为体积流率振幅;${{\tilde{U}}_{1}}$、$\tilde{p}$分别为${{p}_{1}}$、${{U}_{1}}$的共轭复数;θ为${{p}_{1}}$、${{U}_{1}}$之间的相位差。
2.3.2 总能流
总能流是热声系统中涉及声功流和热量流的总和,结合热声线性理论,其表达式如下：
$ {{{\dot{H}}}_{2}}\left( x \right)=\frac{1}{2}Re\left\{ {{p}_{1}}{{{\tilde{U}}}_{1}}\left[ 1-\frac{{{f}_{k}}-{{f}_{\mu }}}{\left( 1-{{f}_{\mu }} \right)\left( 1+\sigma \right)} \right] \right\}+ \left[ \begin{align} & \frac{{{\rho }_{\text{m}}}{{c}_{p}}}{2\omega A\left( 1-{{\sigma }^{2}} \right){{\left| 1-{{f}_{\mu }} \right|}^{2}}}Im\left( \sigma {{f}_{\mu }}+{{f}_{k}} \right) \\ & -Ak-{{A}_{s}}{{k}_{s}} \\ \end{align} \right]\frac{\text{d}{{T}_{\text{m}}}}{\text{d}x} $ (15)
式中：${{A}_{s}}$为固体接触面积;${{k}_{s}}$为固体热传导系数;Re表示实部;Im表示虚部。
结合式（11）~ 式（15）即可求解热声系统中沿程分布的压力、体积流率、温度、压力振幅与体积流率之间的相位差以及声功等值。
本文采取的声功测量方法为可变负载法[2],其测量装置主要有压力传感器、针阀和气库构成,其中针阀是主要耗功部件,气库与热声发动机之间通过针阀连接。通过测量连接处热声发动机的压力波动值P1和气库内的压力波动值P2可以得到通过连接管路和针阀的体积流率U：
$U=\frac{i\omega V{{P}_{2}}}{\gamma {{P}_{\text{m}}}}$ (16)
式中：V为气库容积;P2气库内的压力幅值;$\gamma $为工质的热容比;Pm为工质的平均压力,消耗在针阀上的声功为：
$E=\frac{1}{2}Re\left[ {{{\tilde{p}}}_{1}}{{U}_{1}} \right]=\frac{\omega V\left| {{p}_{1}} \right|\left| {{p}_{2}} \right|\sin \varphi }{2\gamma {{p}_{\text{m}}}}$ (17)
式中：$\varphi $为P1和P2处压力波动的相位差。
3 实验结果与讨论
图3展示了谐振管比值为3.5时的双级行波热声热机起振过程的压力振幅变化。
Fig. 3 Pressure amplitude changes of the system when it vibrates图 3 系统起振时的压力振幅变化 |
当回热器热端与冷端的温差约为60℃时振幅突然增大,这是由于当热声热机起振后,其工作气体从起振前的无规则运动变为一定频率的振动,从而表现为振幅突然增大。之后随着温差的不断增大振幅也在持续增大,这说明当温差约为60℃时该热声系统开始起振。
图4展示了谐振管比值为3.5时的双级行波热声热机起振过程的频率变化。从图中可以看到在温差小于60℃时,系统的频率处于紊乱状态,当温差约为60℃时,系统的频率突变为一个定值,之后随着温差的持续增大,系统的频率略有增大,频率变化不到2 Hz,变化并不明显。说明温度对系统的频率变化影响很小。
Fig. 4 Frequency change when the thermoacoustic system vibrates图4 热声系统起振时的频率变化 |
图5展示了该双级行波热声系统的起振温差随谐振管比例的变化,从图中可以看出在谐振管比值为1时,即双级行波热声热机的两个热声核呈中心对称分布时,系统的起振温差高达153℃,这对该系统所能利用的热源温度要求较高,不利于对较低品位热源的利用。之后热声系统的起振温差随着谐振管的比值的增大先减小后增大,在谐振管比例为1:3.5时热声系统的起振温差出现最小值,为59.6℃。这是由于在环路行波热声发动机中共有四个压力振幅和体积流率振幅的相位差为零的纯行波相位点[14],当多级热声热机的热声核恰好处在该热声系统声场的纯行波相位点时,热声系统会有最低的起振温度;不同工质会有不同的起振温度,但存在最低起振温度的趋势是一样的,这是由于决定热声热机声场分布的主要因素是热声热机本身的结构。本次实验中改变谐振管比例实质上是两个热声核从中心对称位置逐渐靠近的过程,在谐振管比例为3.5时,该热声系统的两个热声核约在该热声系统所产生的声场中的纯行波相位点上。当环路行波热声系统的热声核处于系统所产生的声场中的纯行波相位点时,系统起振时的阻抗将大幅降低,进而将导致系统的起振温度也大幅降低。从图中可以看出谐振管比值从1变化到3.5时,起振温差降低了约93℃,这对该热声系统利用较低品位热源的能力有了较大的提升。
Fig. 5 Variation of the temperature difference between the onset of vibration and the proportion of the resonance tube图 5 起振温差随谐振管比例的变化 |
图6展示了该双级行波热声系统的起振频率随谐振管比例的变化,从图中可以看到,随着谐振管比例的逐渐增大,该热声系统的频率略有增加,但变化的幅度并不大,约为5 Hz。这是由于当两个热声核逐渐靠近时,连接两个热声核之间的谐振管管长发生变化,即两个热声核靠近端的谐振管管长变短,两个热声核远离端的谐振管管长变长,从而导致该双级行波热声系统的起振频率略有增加。
Fig. 6 Variation of the starting frequency with the proportion of the resonance tube图 6 起振频率随谐振管比例的变化 |
图7展示了不同谐振管比例的双级行波热声系统的压比随温差的变化。从图中可以看出该双级行波热声系统的谐振管比例从1.5到4变化的过程中,压比先增大后减小。在比例为3.5时,在相同温差时压比表现最好,这是由于在此位置时系统中的行波分量较其他位置时的行波分量要大,从而表现出压比最大。这也说明当双级行波热声发动机采用非对称结构、谐振管比例为3.5时,双级行波热声发动机具有较好的性能。
Fig. 7 Variation of pressure ratio with temperature difference of thermoacoustic system with different resonance tube ratios图 7 不同谐振管比例的热声系统的压比随温差的变化 |
图8展示了在双级行波热声系统中加入负载后在谐振管之比为1:3和1:3.5两个位置上的声功随温差变化规律。从图中可以看出随着回热器冷热端温差的逐渐增大,两个位置上的声功也不断增大,但是谐振管比值为3.5时的声功明显优于谐振管比值为3时的声功。这是由于在谐振管比值为3.5时热声系统的压力振幅与体积流率振幅的夹角θ比在谐振管比值为3时的θ要小,根据式（14）可知,热声系统的压力振幅与体积流率振幅的夹角θ越小系统产生的声功越大。这也再次表明当谐振管比值为3.5时的双级行波热声热机对较低温度品位热源的利用潜力。在本次实验中虽然已经证明在谐振管比例为1:3.5时该热声系统具有良好的性能,但就提取的声功而言并不是很理想,这与提取声功的位置选取有很大的关系。
Fig. 8 Variation of sound work with temperature difference of thermoacoustic system with different resonant tube ratios图 8 不同谐振管比例的热声系统的声功随温差的变化 |
4 结论
对双级环路行波热声热机进行了两个热声核相对位置变化的实验研究。通过改变两个热声核的相对位置参数对该热声系统的起振温差、起振频率、压比、声功进行探讨,得到以下结论：
（1）随着两个热声核从中心对称位置逐渐靠近,系统起振时的阻抗发生很大变化,阻抗变化表现为起振温度的变化,该双级环路行波热声热机的起振温度先下降再上升,在谐振管之比为1:3.5的位置处存在最低的起振温度,最低起振温度为59.6℃。
（2）随着两个热声核从中心对称位置逐渐靠近,该双级环路行波热声热机的起振频率逐渐变大,但不超过5 Hz,其起振频率主要受限于工作气体和系统长度,热声核位置的相对变化对起振频率的影响不大。
（3）随着两个热声核从中心对称位置逐渐靠近,其系统声场发生很大变化,系统声场的变化直接影响系统的性能,系统性能主要以压比、声功等表现,该双级环路行波热声热机起振后的压比先增大后减小;在相同温差时谐振管之比为1:3.5位置的压比优于其他位置处的压比,且所产生的声功也优于其他位置。
