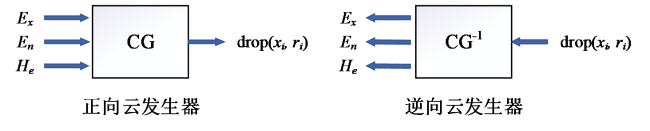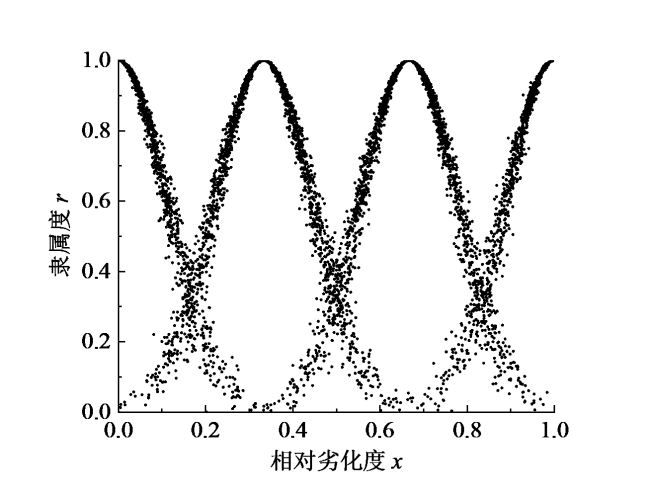0 引言
经济园区化、园区产业化、产业集聚化已成为世界经济发展的趋势,产业园区在经济发展的同时面临着节能减排的社会责任[1]。利用合理的评价模型,从能源、环境、经济等多方面的效益进行研判,对于优化园区能源结构、保障园区绿色稳健发展尤为重要,因此有必要对园区能源系统评价方法进行深入研究。
目前,组合多种评价方法对园区能源系统评价问题开展研究已成为主流趋势。组合评价法能够结合主观评价法与客观评价法的优点,得出更加可靠的评价结果,目前被广泛应用的评价模型组合包括熵值-灰色关联法、层次分析（the analytic hierarchy process, AHP）-逼近理想解排序法（technique for order preference by similarity to an ideal solution, TOPSIS）等,这些组合评价方法以评价指标为结合点实现各个方法的耦合,实现了对传统单一评价法的改进。赵鹏翔等[2]结合网络分析法（analytic network process, ANP）与熵权法对指标进行了赋权,综合考虑了主观赋权与客观赋权,并采用德尔菲法拟合评分函数对方案进行排序。张涛等[3]在赋权方法基础上综合考虑了主客观权重,结合熵权法与专家评价法,并分别设置了侧重能源、经济、环保的专家评价权重,但对方案排序方法的处理较为单一,直接令评价矩阵与权重向量相乘得出各方案评分,很大程度上弱化了评估的模糊性问题。韩中合等[4]应用熵权法与灰色关联分析法,通过对指标赋权的方式对灰色关联法进行了改进,但没有结合主观赋权,仅通过指标的差异程度赋权,不具备代表性。赵凤展等[5]结合序关系法与变异系数法针对多能互补能源系统展开综合评价,为多能互补能源系统的优化与运行提供了理论参考,许龙等[6]建立了包含资源禀赋在内的评价指标体系,并采用AHP-熵权- TOPSIS组合法对系统进行综合评价,能够为建立更加合理可靠的可再生能源系统提供决策依据。以上文献的主要采用方法汇总于表1。
Table 1 Main evaluation methods used in the existing literature表1 现有文献中主要使用的评价方法 |
| 文献 | 主要采用方法 | 是否考虑组合赋权 | 是否考虑评价的模糊性与随机性 |
|---|---|---|---|
| [2] | 网络分析法,熵权法 | 是 | 否 |
| [3] | 熵权法,专家评价法 | 是 | 否 |
| [4] | 熵权法,灰色关联分析法 | 否 | 否 |
| [5] | 序关系法与变异系数法 | 是 | 否 |
| [6] | 层次分析法,熵权法,逼近理想解法 | 是 | 否 |
以上组合评价方法都是在得到各指标权重后通过精确的隶属度函数计算待评价方案与理想最优方案的隶属度得到最终评价结果,传统的隶属度函数虽然能够得到精确的方案评分,但并没有充分考虑实际评价过程的模糊性与随机性。云模型是一种基于正态分布和钟型隶属函数的新兴评价方法,由李德毅院士首次提出[7],其不再受限于建立隶属函数而是通过构造正态隶属度分布的期望函数进行评价,拥有比模糊隶属度函数更强的普遍适用性,且已经被广泛应用于各种情景的综合评价,如水质评价[8]、国家电力发展评价[9]、不确定性评价[10]、投资风险评价[11]。如图1的方法框架所示,本文基于云模型,在指标劣化度计算以及输入评分等级数字特征的基础之上生成评价云,通过构造的期望函数计算指标隶属度矩阵,并结合博弈论方法建立的最优化权重向量得到各方案相对于评分等级的隶属度,根据最大隶属度原则得出方案评分等级,完成定量数据和定性概念之间的不确定转换。
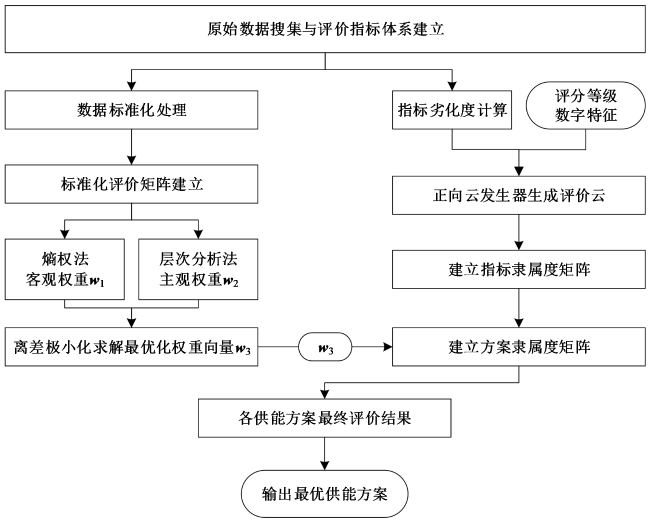
Fig. 1 Game theory-cloud model evaluation method framework图1 博弈论-云模型评价方法框架图 |
1 基于博弈论的组合权重方法
1.1 标准化评价矩阵构建
对园区能源系统进行评价主要分为能源、经济、环境三个类别[12],本文从这三个类别选取一次能源利用率（I1）、节能率（I2）、系统初投资（I3）、年度化成本（I4）、CO2排放量（I5）、SO2排放量（I6）、NOx排放量（I7）这7个具有代表性的指标对园区能源系统进行评价,其中I1、I2为正向指标,I3、I4、I5、I6、I7为负向指标。m个园区供能方案与n个评价指标共同组合构成初始评价矩阵$B=\text{ }\!\!\{\!\!\text{ }{{X}_{ij}}\left| i=1,\cdots ,m;j=1,\cdots ,n \right.\}$,式中Xij为第i个方案对应第j个指标的值。
为消除指标间的不可公度,建立标准化评价矩阵,需要对指标进行标准化处理。
对于正向指标：
${{x}_{ij}}=\frac{{{X}_{ij}}-\text{min}\left( {{X}_{1j}},\cdots ,{{X}_{nj}} \right)}{\text{max}\left( {{X}_{1j}},\cdots ,{{X}_{nj}} \right)-\text{min}\left( {{X}_{1j}},\cdots ,{{X}_{nj}} \right)}$ (1)
对于负向指标：
${{x}_{ij}}=\frac{\text{max}({{X}_{1j}},\cdots ,{{X}_{nj}})-{{X}_{ij}}}{\text{max}({{X}_{1j}},\cdots ,{{X}_{nj}})-\text{min}({{X}_{1j}},\cdots ,{{X}_{nj}})}$ (2)
式中：xij为标准化评价矩阵内的元素。经初始评价矩阵的标准化处理后得到标准化评价矩阵$R=\text{ }\!\!\{\!\!\text{ }{{x}_{ij}}\left| i=1,\cdots ,m;j=1,\cdots ,n \right.\text{ }\!\!\}\!\!\text{ }$。
1.2 主、客观权重集建立
指标赋权方法主要分为客观赋权法与主观赋权法,客观赋权法主要依据评价矩阵所提供的信息量对指标进行赋权,不受人为因素干扰;主观赋权法主要依据专家自身经验,以专家打分的形式建立判断矩阵并对判断矩阵进行处理得到指标权重。
熵权法[13]根据以下算法得到标准化评价矩阵权重向量w1：
${{p}_{ij}}=\frac{{{x}_{ij}}}{\sum\limits_{i=1}^{m}{{{x}_{ij}}}}$ (3)
${{E}_{j}}=-\frac{1}{\text{ln}m}\sum\limits_{i=1}^{m}{{{p}_{ij}}}\text{ln}{{p}_{ij}}$ (4)
${{w}_{1}}=\frac{1-{{E}_{j}}}{\sum\limits_{j=1}^{n}{\left( 1-{{E}_{j}} \right)}}$ (5)
式中：pij为归一化评价矩阵内的元素;Ej为各评价指标的信息熵,信息熵越大表明指标差异程度大,提供信息多。当xij = 0时,令${{p}_{ij}}\text{ln}{{p}_{ij}}=0$。
层次分析法[14]依据专家对指标间相对重要性的评分构造判断矩阵$A=\{{{A}_{st}}\left| s=1,\cdots ,n;t=1,\cdots ,n \right.\}$。判断矩阵中的元素Ast代表指标Is相对指标It重要程度的数值,通常采用1 ~ 9的相对比较标度。根据以下算法得到层次分析法权重向量w2：
${{a}_{st}}=\frac{{{A}_{st}}}{\sum\limits_{s=1}^{n}{{{A}_{st}}}}$ (6)
${{w}_{2}}=\left\{ {{w}_{s}}\left| {{w}_{s}}=\frac{1}{n}\sum\limits_{t=1}^{n}{{{a}_{st}}} \right. \right\}$ (7)
式中：ast为归一化判断矩阵内的元素;ws为第s个指标的权重。根据层次分析赋权法计算范式,为检验判断矩阵中各元素的协调性,在得到权重向量后应进行一致性检验：
${{C}_{R}}=\frac{{{\lambda }_{\text{max}}}-n}{\left( n-1 \right)\text{RI}}$ (8)
${{\lambda }_{\text{max}}}=\sum\limits_{s=1}^{n}{\frac{{{A}_{s}}{{w}_{2}}^{T}}{n{{w}_{s}}}}$ (9)
式中：RI为平均随机一致性指标,取值如表2所示; CR为一致性检验指标,当CR < 1时,认为判断矩阵在一致性方面符合要求,否则必须重新调整判断矩阵直至符合一致性标准为止;As为矩阵A的第s个行向量;w2T为权重向量w2的转置。
Table 2 Random consensus index表2 随机一致性指标 |
| 矩阵阶数 n | RI值 |
|---|---|
| 1 | 0.00 |
| 2 | 0.00 |
| 3 | 0.52 |
| 4 | 0.89 |
| 5 | 1.12 |
| 6 | 1.26 |
| 7 | 1.36 |
| 8 | 1.41 |
| 9 | 1.46 |
1.3 博弈论组合权重
上述两种赋权方法各有优势,熵权法刻画评价矩阵包含的客观信息量,但在实际评价的过程中由于所获取数据的模糊性与随机性,基于评价矩阵所包含信息量建立的权重集可能与实际指标重要情况相悖。层次分析法基于专家打分建立的判断矩阵建立权重集,在一定程度上代表了指标的相对重要性,但主观性较强。博弈论组合权重方法借鉴合作博弈思想[15],将不同的权重集视作同一联盟的不同决策,组合主、客观权重,结合主观判断与客观事实,实现两者的优势互补。
根据上一节的算法得到主客观权重向量集$W=\{{{w}_{1}};{{w}_{2}}\}$,为得到最优化权重向量w3,即实现w3与w1、w2的离差极小化,根据矩阵的微分性质得到优化一阶导数条件为：
$\sum\limits_{i=1}^{2}{{{\alpha }_{i}}}{{w}_{i}}w_{j}^{T}={{w}_{i}}w_{j}^{T}$ (10)
解出系数αi后进行归一化处理得到αi*,最终得出博弈论权重向量w3：
$\alpha _{i}^{*}=\frac{{{\alpha }_{i}}}{\sum\limits_{i=1}^{2}{{{\alpha }_{i}}}}$ (11)
${{w}_{3}}=\sum\limits_{i=1}^{2}{\alpha _{i}^{*}{{w}_{i}}}$ (12)
2 基于云模型的模糊评价方法
2.1 云模型理论
李德毅院士提出的云模型[7]以语言值为切入点,集成概念的随机性（发生的概率）与模糊性（边界的亦此亦彼）实现了定量数值与定性概念之间的转换,目前已被广泛应用于综合评价与算法改进。云模型区别于传统模糊评价模型的精确函数表示,采用数字特征参数来表征概念的不确定性,并通过构造正态分布的隶属度期望函数实现数据到概念的映射,避免了精确函数表示所带来的模糊性缺失、被完全纳入精确数学范畴的现象。
云模型定义：假设论域X={x}是一个数值集合,C是论域X中的定性概念之一。若数值x是对于定性概念C的一次随机实现,x对C的隶属度$\mu \left( x \right)\in [0,1]$是一组趋向于稳定的随机数,则由论域上所有的x组成的最终形式被称为“云”,其中每一个x为一个“云滴”。在云模型中,期望Ex、熵En、超熵He这三个数字特征被用于刻画定性概念的定量特征,其中期望是论域X={x}中最能够代表这个定性概念的点,是定性概念基本确定性的度量;熵表征定性概念的不确定性,反映了概念在论域X={x}中能够被接受的范围;超熵是熵的不确定程度的度量。如图2所示,在期望相同的情况下,熵En越大该定性概念被接受的范围越大;超熵He越大云滴分布越分散,熵的不确定程度越高。
Fig. 2 Distribution characteristics of clouds with different digital characteristics图2 不同数字特征的云滴分布特征 |
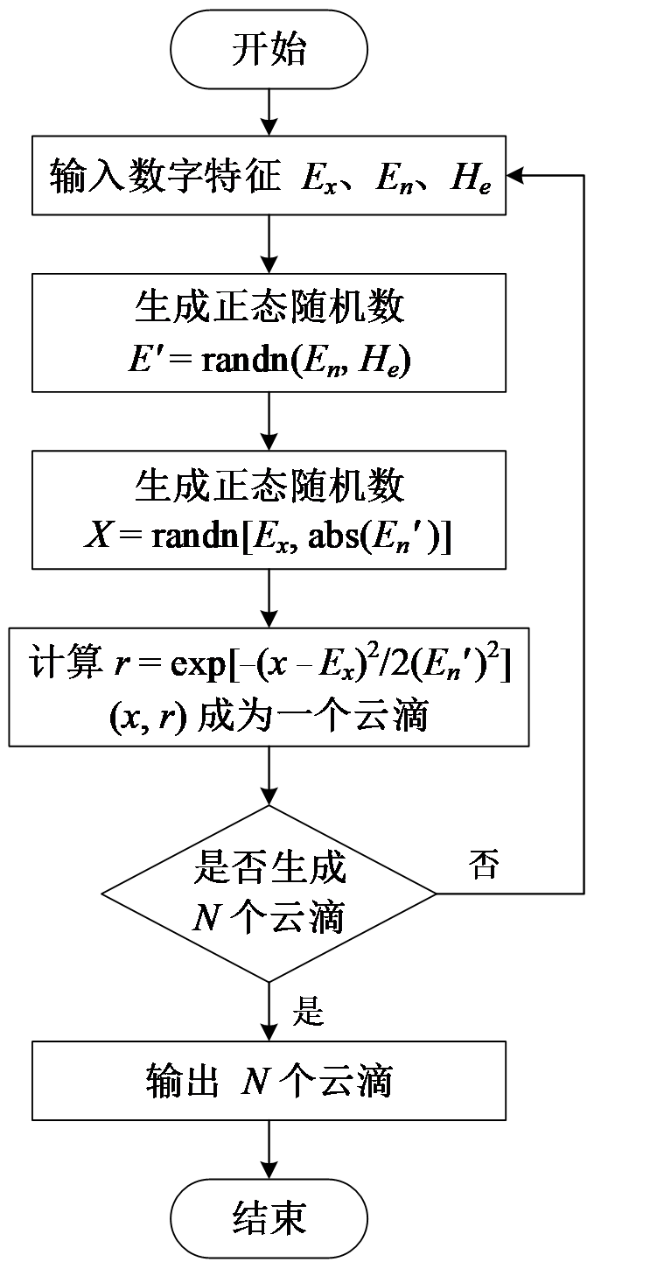
2.2 评价云与隶属度矩阵构建
Fig. 3 Cloud generator图3 云发生器 |
本文采用正向云发生器,主要通过以下算法实现[17]：①输入数字特征Ex、En、He;②生成以En为期望、He为标准差的正态随机数${{{E}'}_{n}}$;③生成以Ex为期望、abs(${{{E}'}_{n}}$)为标准差的正态随机数x;④计算$r=\text{exp}\left[ \frac{-{{\left( x-{{E}_{x}} \right)}^{2}}}{2{{\left( {{{{E}'}}_{n}} \right)}^{2}}} \right]$,并令r为相对于概念C的隶属度;⑤实现了定量值x对于概念C的量化,点（x, r）成为一个云滴;⑥重复步骤① ~ 步骤⑤,直至生成N个云滴。
正向云模型程序流程图如图4所示。
Fig. 4 Forward cloud model program flow chart图4 正向云模型程序流程图 |
Table 3 Numerical features of rating scale表3 评分等级数字特征 |
| 评分等级 | 取值区间 | Ex | En | He |
|---|---|---|---|---|
| 1级 | (0, a) | 0 | 2a/3 | 0.01 |
| 2级 | [a, b) | (a+b)/2 | (b-a)/3 | 0.01 |
| 3级 | [b, c) | (b+c)/2 | (c-b)/3 | 0.01 |
| 4级 | [c, d] | d | 2(d-c)/3 | 0.01 |
Fig. 5 The four evaluation clouds of the index deterioration degree图5 指标劣化度的4朵评价云 |
生成评价云后指标的相对劣化度实现了对各个评分等级的隶属度的映射,通过计算第i个指标相对于第j个评分等级的隶属度rij,得到方案集合中的其中一个方案的隶属度矩阵$\mathbf{R}=\{{{r}_{ij}}\left| i=1,\cdots ,7;j=1,\cdots ,4\} \right.$,结合上节得到的综合了主客观权重的博弈论权重向量w3计算该方案相对于各评分等级的隶属度向量：
$\begin{align} & m{{v}_{1}}={{w}_{3}}\times R=\left[ \begin{matrix} {{w}_{31}} & \cdots & {{w}_{37}} \\ \end{matrix} \right]\left[ \begin{matrix} {{r}_{11}} & \cdots & {{r}_{14}} \\ \vdots & \ddots & \vdots \\ {{r}_{71}} & \cdots & {{r}_{74}} \\ \end{matrix} \right] \\ & =[m{{v}_{11}}\ \ m{{v}_{12}}\ \ m{{v}_{13}}\ \ m{{v}_{14}}] \end{align}$ (13)
式中：mv11、mv12、mv13、mv14分别代表方案1对应评分等级的1级、2级、3级、4级的隶属度。以上即为得到一个方案的最终隶属度向量的计算范式,通过同样的方法可以得到其他方案的隶属度向量。根据最大隶属度原则,评判各方案所处等级,最终得出评价结果。
3 案例分析
选择广东省华南现代中医药园区作为研究案例,根据园区现有基础负荷数据、供能方案以及设计的优化供能方案进行园区能源系统综合评价。中医药园区的主要负荷需求为热负荷与电负荷,现有供热方式为生物质锅炉供热。2019年总热负荷为蒸汽10 641.06 t;年电负荷为5 950 338.05 kW∙h;中医药城设置有光伏发电设备,年总发电量为648 470.90 kW∙h。根据园区实际情况设置6种供能方案。各方案基础数据如表4所示。
Table 4 Basic data of energy supply plans表4 各供能方案基础数据 |
| 方案 | 一次能源利用率 / % | 节能率 / % | 系统初投资 / 万元 | 年度化成本 / 万元 | CO2排放量 / t | NOx排放量 / t | SO2排放量 / t |
|---|---|---|---|---|---|---|---|
| 1 | 52.60 | 8.62 | 1 150 | 736 | 8 663.24 | 14.20 | 15.23 |
| 2 | 53.80 | 14.82 | 1 670 | 727 | 8 101.39 | 13.15 | 13.92 |
| 3 | 62.48 | 26.65 | 1 954 | 773 | 6 538.58 | 8.64 | 7.83 |
| 4 | 72.05 | 36.39 | 2 196 | 876 | 5 049.33 | 3.28 | 0.00 |
| 5 | 74.49 | 38.47 | 2 087 | 808 | 3 482.58 | 5.53 | 6.24 |
| 6 | 48.06 | 0.00 | 1 137 | 474 | 9 058.27 | 16.98 | 21.19 |
方案1：生物质锅炉承担全部热负荷,电网承担全部电负荷。方案2：在方案1的基础上增添光伏发电装置,并优先消纳光伏发电,剩余电负荷由电网补足,生物质锅炉承担全部热负荷。方案3：在方案2的基础上加入燃气轮机,生物质锅炉与燃气轮机承担热负荷,供热比例为1:1,光伏与燃气轮机满足电负荷,不足电负荷从电网购入。方案4：采用以电定热策略,优先消纳光伏发电,剩余电负荷全部由燃气轮机承担,同时通过燃气轮机余热回收满足热负荷。方案5：采用以热定电策略,燃气轮机承担全部热负荷,同时与光伏发电共同满足部分电负荷,剩余电负荷由电网补平衡。方案6：参考方案,燃煤锅炉满足热负荷,电网供电满足电负荷。
对数据进行无量纲处理,由式（1）和式（2）得到标准化评价矩阵R：
$R=\left[ \begin{array}{*{35}{r}} 0.173 & 0.225 & 0.986 & 0.349 & 0.073 & 0.204 & 0.282 \\ 0.218 & 0.386 & 0.497 & 0.371 & 0.173 & 0.281 & 0.344 \\ 0.545 & 0.692 & 0.230 & 0.258 & 0.452 & 0.608 & 0.630 \\ 0.906 & 0.944 & 0.002 & 0.002 & 0.718 & 0.998 & 0.998 \\ 0.998 & 0.998 & 0.105 & 0.170 & 0.998 & 0.834 & 0.705 \\ 0.002 & 0.002 & 0.998 & 0.998 & 0.002 & 0.002 & 0.002 \\ \end{array} \right]$
评价矩阵已对效益性指标和消耗性指标分别进行了标准化处理,其中数据数值越大越优,越小越劣。如表4所示,除参考方案6之外,方案1一次能源利用率、节能率最劣,系统初投资最优,这是由于系统采取的生物质锅炉供汽、电网直接供电的方案,系统初投资低,仅需支出基本费用以及生物质锅炉相关配套费用;但由于采取电网供电,导致供能系统的能源利用效率低下,同时,大规模采用传统电网供电还存在CO2、SO2、NOx排放量高的问题,导致对应指标数据表现不佳。方案2在方案1的基础上加入了光伏发电,且优先消纳光伏发电,不足电负荷从电网购入,由于采取了清洁能源发电,系统的节能率、污染物排放方面的指标数值有一定程度的提升,但受场地限制导致规模不大以及天气影响等因素导致光伏发电总量不大,因此较方案1提升不大,且经济指标评分下降。方案3在方案2的基础上采用燃气轮机供应一部分电负荷,并对燃气轮机进行余热回收供汽,与生物质锅炉共同满足蒸汽需求。此方案大幅减少了外部购电,因此在节能、二氧化碳以及其他污染物排放方面较方案1、方案2有所提升,但系统初投资评分有所降低,这是由于设备的增加,系统初投资增加。方案4和方案5分别采取以电定热策略与以热定电策略,在方案3的基础上增大了燃气轮机的容量,通过热电联供的方式,大幅度提升了能源利用效率,同时系统也不再需要生物质锅炉补足剩余热负荷,因此在能源指标与环境指标上较前三个方案大幅提升,但由于燃气轮机的容量提升以及天然气价格较高等因素,系统初投资以及年度化成本也都有较大提高。
建立标准化决策矩阵R后,根据博弈论组合赋权方法建立指标权重,按照熵权法式（3）~ 式（5）建立${{w}_{1}}=\left[ \begin{matrix} 0.147 & 0.118 & 0.166 & 0.149 & 0.180 & 0.129 & 0.109 \\ \end{matrix} \right]$权重向量。按照层次分析法式（6）~ 式（7）构造判断矩阵：
$A=\left[ \begin{matrix} 1 & 1 & 2 & 3 & 1/3 & 4 & 5 \\ 1 & 1 & 2 & 3 & 1/3 & 4 & 5 \\ 1/2 & 1/2 & 1 & 2 & 1/4 & 3 & 4 \\ 1/3 & 1/3 & 1/2 & 1 & 1/5 & 2 & 3 \\ 3 & 3 & 4 & 5 & 1 & 6 & 7 \\ 1/4 & 1/4 & 1/3 & 1/2 & 1/6 & 1 & 2 \\ 1/5 & 1/5 & 1/4 & 1/3 & 1/7 & 1/2 & 1 \\ \end{matrix} \right]$
得到${{w}_{2}}=\left[ \begin{matrix} 0.177 & 0.177 & 0.113 & 0.073 & 0.379 & 0.048 & 0.033 \\ \end{matrix} \right]$权重向量,根据一致性检验式（8）和式（9）对得到的权重与判断矩阵进行检验,得到${{\lambda }_{\text{max}}}=7.178$、$\text{RI}=0.029$、${{C}_{R}}=0.0218<0.1$,故通过一致性检验,w2即为主观权重向量。按照博弈论组合权重方法对两组权重向量进行离差极小化,实现最优化权重向量,得到$\alpha _{1}^{*}=-0.2058$,$\alpha _{2}^{*}=1.2058$, ${{w}_{3}}=\left[ \begin{matrix} 0.183 & 0.189 & 0.102 & 0.058 & 0.420 & 0.032 & 0.017 \\ \end{matrix} \right]$。
如图6所示,熵权法与层次分析法对不同指标的赋权差异程度较大,体现了评价矩阵所包含的客观信息量与专家主观经验的差异性,若采取单一的赋权方法则会有较大误差,难以得到客观公正的评价结果,博弈论方法借鉴合作博弈思想,结合主客观权重得到最优化权重。最终得到的权重结果为CO2排放量权重最大,符合当前节能减碳的企业管控环境,而NOx与SO2由于一段时间以来的技术积累,各方案的相关排放量已经达到了一个很低的水平,对方案优劣性的影响不大,因此权重较低,而一次能源利用率、年度化成本处于中间位置。
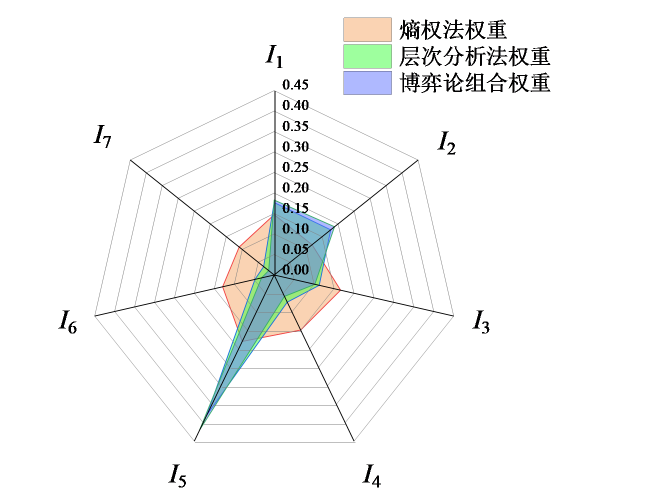
Fig. 6 Indicator weights obtained by three weighting methods图6 三种赋权方法得到的指标权重 |
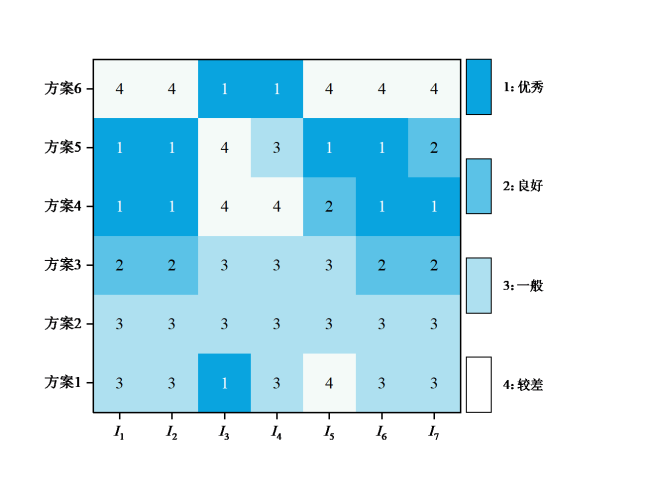
Fig. 7 Scoring grades for each scheme indicator图7 各方案指标评分等级 |
Table 5 Membership of each program index表5 各方案指标隶属度 |
| 指标 隶属度 | 方案1 | 方案2 | 方案3 | 方案4 | 方案5 | 方案6 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1级 | 2级 | 3级 | 4级 | 1级 | 2级 | 3级 | 4级 | 1级 | 2级 | 3级 | 4级 | 1级 | 2级 | 3级 | 4级 | 1级 | 2级 | 3级 | 4级 | 1级 | 2级 | 3级 | 4级 | |
| I1 | 0.000 | 0.000 | 0.352 | 0.298 | 0.000 | 0.000 | 0.586 | 0.145 | 0.000 | 0.551 | 0.162 | 0.000 | 0.700 | 0.098 | 0.000 | 0.000 | 1.000 | 0.012 | 0.000 | 0.000 | 0.000 | 0.000 | 0.012 | 1.000 |
| I2 | 0.000 | 0.000 | 0.622 | 0.128 | 0.000 | 0.041 | 0.895 | 0.002 | 0.021 | 0.975 | 0.005 | 0.000 | 0.881 | 0.044 | 0.000 | 0.000 | 1.000 | 0.012 | 0.000 | 0.000 | 0.000 | 0.000 | 0.012 | 1.000 |
| I3 | 1.000 | 0.012 | 0.000 | 0.000 | 0.000 | 0.337 | 0.312 | 0.000 | 0.000 | 0.000 | 0.665 | 0.111 | 0.000 | 0.000 | 0.012 | 1.000 | 0.000 | 0.000 | 0.123 | 0.635 | 0.979 | 0.020 | 0.000 | 0.000 |
| I4 | 0.000 | 0.000 | 0.012 | 1.000 | 0.000 | 0.000 | 0.018 | 0.987 | 0.000 | 0.088 | 0.728 | 0.001 | 1.000 | 0.012 | 0.000 | 0.000 | 0.762 | 0.077 | 0.000 | 0.000 | 0.000 | 0.185 | 0.509 | 0.000 |
| I5 | 0.000 | 0.000 | 0.064 | 0.808 | 0.000 | 0.000 | 0.353 | 0.298 | 0.000 | 0.155 | 0.565 | 0.000 | 0.040 | 0.898 | 0.002 | 0.000 | 1.000 | 0.012 | 0.000 | 0.000 | 0.000 | 0.000 | 0.012 | 1.000 |
| I6 | 0.000 | 0.000 | 0.509 | 0.185 | 0.000 | 0.002 | 0.894 | 0.041 | 0.002 | 0.870 | 0.047 | 0.000 | 1.000 | 0.012 | 0.000 | 0.000 | 0.330 | 0.320 | 0.000 | 0.000 | 0.000 | 0.000 | 0.012 | 1.000 |
| I7 | 0.000 | 0.002 | 0.899 | 0.040 | 0.000 | 0.015 | 0.996 | 0.008 | 0.004 | 0.947 | 0.028 | 0.000 | 1.000 | 0.012 | 0.000 | 0.000 | 0.029 | 0.943 | 0.004 | 0.000 | 0.000 | 0.000 | 0.012 | 1.000 |
图7直观反映出在赋权之前各个指标的评价等级,其中方案4和方案5指标被评为优秀的数量最多,方案6的能源类别和环境类别的指标都被评为较差,只有经济指标由于投资较少而被评为优秀。从标准化评价矩阵的建立到指标相对评分等级隶属度再到各指标评分等级图,实现了输入的定量参数到定量概念的转变。生成指标评分等级这一云模型中间环节是该模型区别于其他模糊评价模型的优点之一,对各方案的每个指标进行定性评估并输出结果,保留了原始评价矩阵的信息,在后续分析最终评价结果时能够更加清晰地表述各评价指标以及指标权重对最终结果的影响。
在得到指标隶属度矩阵后结合博弈论组合权重模型生成的指标权重向量计算方案隶属度矩阵,计算过程如公式（13）,最终结果为：
$mv=\left[ \begin{array}{*{35}{r}} 0.101 & 0.003 & 0.298 & 0.425 \\ 0.000 & 0.042 & 0.559 & 0.154 \\ 0.004 & 0.394 & 0.382 & 0.016 \\ 0.360 & 0.404 & 0.003 & 0.160 \\ 0.802 & 0.036 & 0.032 & 0.083 \\ 0.160 & 0.002 & 0.010 & 0.840 \\ \end{array} \right]$
根据最大隶属度原则,方案1、方案2、方案3、方案4、方案5、方案6的评分等级分别为4级、3级、2级、2级、1级、4级,故方案5为最优方案。为验证评价结果的准确性,还选择了博弈论-逼近理想解排序法[14]、博弈论-灰色关联法[18]对评价结果进行验证,两种方法的算法有所差异但评价逻辑类似,都是通过构建各待评价方案相对理想方案的精确线性隶属度函数来得出评价结果,且已较为成熟并被广泛应用。为方便对比与说明,结合隶属度矩阵mv与限值向量$\theta =\left[ \begin{matrix} 100 & 75 & 50 & 25 \\ \end{matrix} \right]$,得到本文方法和两种验证方法的最终评分与各方案排序见表6。
Table 6 Comparison of the evaluation results of various methods表6 各方法评价结果对比 |
| 验证方法 | 方案1 | 方案2 | 方案3 | 方案4 | 方案5 | 方案6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 评分 | 排序 | 评分 | 排序 | 评分 | 排序 | 评分 | 排序 | 评分 | 排序 | 评分 | 排序 | |
| 博弈论-逼近理想解排序法 | 30.50 | 4 | 28.52 | 6 | 48.93 | 3 | 63.39 | 2 | 72.02 | 1 | 30.37 | 5 |
| 博弈论-灰色关联法 | 43.37 | 5 | 41.09 | 6 | 50.41 | 3 | 69.56 | 2 | 88.44 | 1 | 44.00 | 4 |
| 博弈论-云模型法（本文方法） | 35.83 | 5 | 34.89 | 6 | 49.46 | 3 | 70.44 | 2 | 86.58 | 1 | 37.63 | 4 |
两种验证方案均得到与本文验证方法基本一致的结果,即方案5为最优方案,其中博弈论-灰色关联法排序结果与本文方法完全一致,表明博弈论-云模型评价方法的功能与传统园区评价方法相似,推导结果可靠。且基于云模型的评价方法把构造精确的隶属函数放宽到了构造隶属度期望函数,更具有普遍适用性,更简单直接地完成了定性与定量的转换过程。在评价过程中对各方案指标的定性描述也有助于决策者对具体指标进行调整,为园区优化供能方案提供支撑。
4 结论
基于云模型与合作博弈理论建立了园区能源系统评价方法,通过借鉴合作博弈思想综合主客观权重建立最优化权重向量,基于云模型输入数字特征Ex、En、He,并分别对4个评价等级生成2 000个云滴得到评价云,计算评价指标劣化度得到指标隶属度矩阵,结合最优化权重向量得到方案隶属度矩阵,根据最大隶属度原则得到各方案评分等级,实现了定量的评价矩阵到定性的评分等级的转换。评价结果表明,在本文建立的方案集中,应当选择方案5,即采用以热定电策略,燃气轮机承担全部热负荷,同时与光伏发电共同满足部分电负荷,剩余电负荷由电网补平衡。并通过模型建立与案例分析得出以下结论：
（1）在建立最优化权重部分采用博弈论组合权重方法,分析表明该方法能够求解客观数据信息熵与主观经验决策最优组合比重,实现了主、客观赋权的统一,避免了单一赋权方法导致的指标权重不精确、不合理现象。
（2）在案例分析部分采用了博弈论-灰色关联法、博弈论-逼近理想解排序法对评价结果进行验证,最终本文采用的博弈论-云模型法得出方案5最终评分为86.58,为最优方案,方案评分排序为方案5 > 方案4 > 方案3 > 方案6 > 方案1 > 方案2。博弈论-逼近理想解排序法与博弈论-灰色关联法得出的方案评分排序分别为：方案5 > 方案4 > 方案3 > 方案1 > 方案6 > 方案2,方案5 > 方案4 > 方案3 > 方案6 > 方案1 > 方案2,验证了本文方法的可靠性。
（3）对基于云模型的模糊评价方法与传统基于精确隶属度函数的模糊评价方法进行分析对比,发现精确的函数曲线实质上弱化了评价的模糊性问题,在实际的评估过程中,概念边界的亦此亦彼性是难以忽略的问题,而云模型的期望隶属度函数同时兼顾了评估的模糊性与随机性。
（4）博弈论-云模型评价方法框架具有普适性,可以通过进一步细化评价指标、增加评分等级、调整主客观赋权方法的方式进一步拓展与优化评价方法,能够良好应用于园区能源系统以及其他各类场景的综合评价,为决策者提供理论支撑。
