0 引言
镶套修复是一种传统的轴颈磨损修复方法[11]。然而,目前还未见将该技术用于在风电机组机舱内直接修复发电机轴颈的报道。这是由于风电机组发电机轴颈修复具有以下难点：风电机组机舱内空间狭小,人员开展修复工作条件受限;机舱随风频繁晃动,因此车削精度难以保证,车削误差相对较大;轴套需提前在地面加工好,结合轴颈的车削误差,现场可能出现无法装配等情况。
本文介绍了一种采用镶套工艺修复磨损的发电机轴颈的方法。该工艺先对磨损的轴颈进行车削,随后将轴套加热,以过盈配合的方式将轴套安装于轴颈上,以恢复轴颈的尺寸和表面精度。该修复工艺对轴颈无热输入,可直接在机舱内对发电机轴颈进行修复,无需吊装,质量可靠、效率高,对于风场尤其是海上风场的经济性具有一定意义。
1 磨损原因
发电机轴颈磨损的根本原因是轴承的内圈与轴颈发生了相对位移。该位移包括两类：一类是轴向位移,即轴承沿着轴颈的中心轴方向朝靠近发电机或远离发电机的方向运动;另一种是轴颈与轴承的旋转不同步,即俗称的“跑圈”。
轴承的内圈与轴颈发生相对位移的原因主要包括以下三个方面。
1.1 轴电流灼伤
风电机组变频器采用脉冲宽度调制（pulse-width modulation, PWM）的调制方式,电压尖峰对应的频率高,因此电流可以通过寄生电容、寄生电感耦合至发电机的轴颈,再传导至轴承的内圈。该电流经过轴颈与轴承的表面时,会在该点产生极高的热量,进而导致该点金属熔化,产生凹坑。风机运行时间越长,凹坑数量越多。当凹坑达到一定数量时,轴承与轴颈配合的紧力减小到一定程度,随即轴承内圈与轴颈发生相对滑动,导致轴颈磨损[12]。
1.2 过盈量减小
发电机轴颈长期处于一种高温高转速的工作状态,轴承在高温状态下发生膨胀,使得内圈与轴颈的过盈量减小,配合的紧力降低,内圈与轴颈之间出现位移[13]。
1.3 轴承损坏
由于风电机组运行工况恶劣,经过一段时间的运行,发电机轴承可能出现保持架断裂、滚道磨损等问题[14]。出现该问题后,轴承自身运行摩擦力大幅增大,增大的摩擦力会作用到轴承内圈与轴颈的配合面,使轴承内圈与轴颈之间出现位移,进而导致磨损。
2 修复工艺
修复工艺流程如图1所示。其中,拆轴承和装轴承有成熟的工艺,本文不再赘述。表面清理需要清除磨损处的杂质,并用清洗剂洗掉残留的润滑油。本节重点对车削、镶套和尺寸检测进行介绍。
Fig. 1 Repairing process图1 修复工艺流程 |
2.1 车削
出厂时,轴颈的长度为l,直径为D。车削时,将其直径由D车削至Df,如图2所示。车床为自主研发产品,可直接安装于机舱内,直接对发电机轴颈进行车削,不需将发电机吊装至地面,以降低修复成本和发电量损失。工程中,发电机轴颈的磨损量不超过3 mm。3 mm的轴套为薄壁套,加工困难,且镶套修复时薄壁套容易损坏。因此,实际工程中将轴套的壁厚设计为10 mm左右,轴颈的车削量相应地设计为7 ~ 10 mm,即轴颈的直径相对于出厂时的值被车削去20 mm。
Fig. 2 Size of the axle journal: (a) before turning; (b) after turning图2 轴颈尺寸：（a）车削前;（b）车削后 |
2.2 镶套
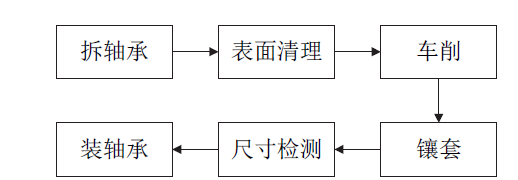
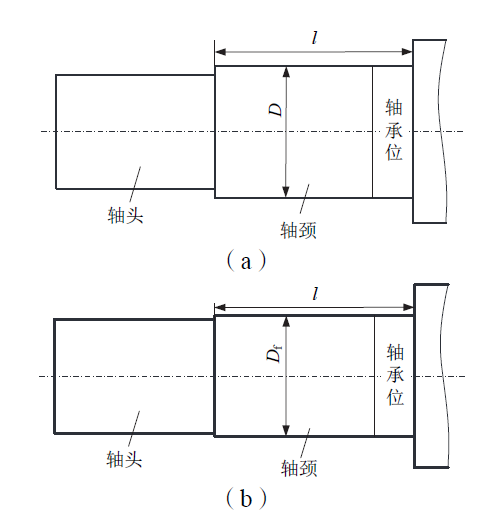
镶套是修复工艺的重要环节,应保证满足以下要求：轴套提前在地面加工,虽然车削后的轴颈存在误差,但轴套可以克服该误差成功安装上去;轴套加热后,可以比较容易地套在轴颈上,冷却后二者过盈配合,而且考虑到风机上的实际情况,加热温度不宜超过300℃;修复后,轴颈的外径满足出厂条件;轴颈不会发生剪断或扭断,即能够承受相应的剪力和扭矩;发电机运行过程中,轴套和轴颈之间不会发生打滑,且轴套与轴颈均不会发生塑性变形。
根据以上要求,求解思路为：选用和轴颈一样的材料加工轴套;以传递扭矩要求和材料不发生塑性形变条件,分别求得过盈配合的最大、最小过盈量,在该范围中选择一组偏差代号,并通过经验公式校核热装法的难度;在此基础上,求得轴颈的直径、轴套的内径以及轴套外径在安装后的变化量,进而求得加工时需要的轴套内径和外径。考虑到轴颈存在车削误差,因此提前在地面加工5个轴套,各轴套的内径根据车削误差的范围而有所不同,确保车削后可有1个轴套成功安装。
2.2.1 初步计算车削后轴颈的直径
基于轴颈的抗扭强度初步确定车削后轴颈的直径[15]。轴颈在扭转时的最大切应力不可超过材料的许用切应力,即
${{\tau }_{\max }}=T/{{W}_{\text{p}}}\le \left[ \tau \right]$ (1)
其中,轴颈的扭转截面系数为
${{W}_{\text{p}}}=\frac{\text{ }\!\!\pi\!\!\text{ }{{D}_{\text{f}}}^{3}}{16}$ (2)
同时,发电机运行时轴颈的扭矩为
$T=9549\frac{P}{n}$ (3)
进而得到
${{D}_{\text{f}}}\ge {{\left( \frac{16T}{\text{ }\!\!\pi\!\!\text{ }[\tau ]} \right)}^{1/3}}$ (4)
一般来说,塑性材料的扭转许用切应力为
$\left[ \tau \right]=0.5\tilde{\ }0.6\left[ \sigma \right]$ (5)
进而可确定Df的最小值。在此基础上,可以初步选定一个Df值。注意Df须大于轴头的直径,否则车削时会将轴头一并车削。
2.2.2 计算最小有效过盈量
为保证轴套与轴颈不打滑,二者之间的最小压力为
${{p}_{\min }}=\frac{2T}{\text{ }\!\!\pi\!\!\text{ }{{D}_{\text{f}}}^{2}l}$ (6)
镶套后,为保证传递扭矩时轴套和轴颈不打滑,轴套内径的最小变化量为
${{e}_{\text{a}\min }}=\frac{{{D}_{\text{f}}}{{C}_{\text{a}}}}{E}{{p}_{\min }}$ (7)
其中：轴套的拉梅系数Ca可以通过式（8）和式（9）计算得到。
${{C}_{\text{a}}}=\frac{1+{{q}_{\text{a}}}^{2}}{1-{{q}_{\text{a}}}^{2}}+\gamma $ (8)
${{q}_{\text{a}}}=\frac{{{D}_{\text{f}}}}{{{d}_{2}}}\approx \frac{{{D}_{\text{f}}}}{D}$ (9)
镶套后,为保证传递扭矩时轴套和轴颈不打滑,轴颈直径的最小变化量为
${{e}_{\text{i}\min }}=\frac{{{D}_{\text{f}}}{{C}_{\text{i}}}}{E}{{p}_{\min }}$ (10)
其中：轴颈的拉梅系数可通过式（11）计算得到。
${{C}_{\text{i}}}=1-\gamma $ (11)
进而可以计算得到轴套与轴颈的最小有效过盈量为
${{\delta }_{\min }}={{e}_{\text{a}\min }}+{{e}_{\text{i}\min }}$ (12)
因此,只要保证轴套与轴颈的实际过盈量δ大于δmin,即可保证二者在发电机运行过程中不会打滑,即
$\delta >{{\delta }_{\min }}$ (13)
2.2.3 计算最大有效过盈量
针对轴套,基于第四强度理论[16],有
${{p}_{\text{a}\max }}=\frac{1-{{q}_{\text{a}}}^{2}}{\sqrt{3+{{q}_{\text{a}}}^{4}}}\sigma $ (14)
针对轴颈,基于第四强度理论,有
${{p}_{\text{i}\max }}=0.5[\sigma ]$ (15)
因此,为保证轴颈与轴套均不发生塑性变形,二者之间的最大压力为
${{p}_{\max }}=\min \{{{p}_{\text{a}\max }},{{p}_{\text{i}\max }}\}$ (16)
镶套后,为保证轴套不发生塑性变形,轴套内径的最大变化量为
${{e}_{\text{a}\max }}=\frac{{{D}_{\text{f}}}{{C}_{\text{a}}}}{E}{{p}_{\max }}$ (17)
同时,为保证轴颈不发生塑性变形,轴颈直径的最大变化量为
${{e}_{\text{i}\max }}=\frac{{{D}_{\text{f}}}{{C}_{\text{i}}}}{E}{{p}_{\max }}$ (18)
进而,可以计算得到轴套与轴颈的最大有效过盈量为
${{\delta }_{\max }}={{e}_{\text{a}\max }}+{{e}_{\text{i}\max }}$ (19)
因此,只要保证轴套与轴颈的实际过盈量δ小于δmax,即可保证二者在发电机运行过程中不会发生塑性变形,即
$\delta <{{\delta }_{\max }}$ (20)
2.2.4 确定过盈量
计算0.5(δmin+δmax),以该数值为基准,在公差表里选择常用的公差配合,确定δ,δ需满足式（13）和式（20）的要求[17]。
考虑到风机内操作的条件有限,本修复工艺要求轴套应较容易装入,因此可选择较小过盈量。可应用式（21）指导判断过盈配合的安装难易程度。
$\Delta t=\frac{\delta +{{\delta }_{0}}}{\alpha \cdot {{D}_{\text{f}}}}$ (21)
其中：加热后的间隙量δ0一般可取1 ~ 2倍δ。根据风机内的实际条件,Δt应小于300℃。若不满足条件,则应适当减小δ。
2.2.5 计算车削后轴颈的尺寸
在确定δ的同时,可直接根据公差表确定Df。此时计算得到的Df与2.2.1节中初步确定的Df非常接近,但会有一个小偏差。以此时确定的Df为准。
2.2.6 计算修复前轴套的尺寸
基于δ,可以计算得到轴套和轴颈之间的实际压力为
$p=\frac{\delta E}{{{D}_{\text{f}}}\left( {{C}_{\text{a}}}+{{C}_{\text{i}}} \right)}$ (22)
因此轴套的外径变化量为
$\Delta d=\frac{2p{{d}_{2}}{{q}_{\text{a}}}^{2}}{E\left( 1-{{q}_{\text{a}}}^{2} \right)}$ (23)
轴套的外径变化后,应与轴颈的出厂直径一致,即
${{d}_{2}}+\Delta d=D$ (24)
根据式（23）和式（24）,即可求得轴套的外径d2。
同时,根据公差表,可以确定轴套的内径d1。考虑到轴颈的车削误差,设最大车削误差为ΔDf,则5个轴套的内径分别设计为${{d}_{1}}-\Delta {{D}_{\text{f}}}$、${{d}_{1}}-\frac{\Delta {{D}_{\text{f}}}}{2}$、${{d}_{1}}$、${{d}_{1}}+\frac{\Delta {{D}_{\text{f}}}}{2}$、${{d}_{1}}\text{+}\Delta {{D}_{\text{f}}}$。车削完成后,根据轴颈的实际尺寸选择合适的轴套。
2.3 尺寸检测
修复后,用游标卡尺检测轴颈的直径,用百分表测量轴颈的跳动。若检测发现不满足要求,则需要对轴套进行切割后,安装新轴套。值得一提的是,在轴套的尺寸和跳动满足要求且车削后的轴颈尺寸满足要求的情况下,修复后可做到不需返修。
3 工程应用
在理论研究的基础上,于某国产品牌风机上开展工程应用。该风机的发电机轴颈出现磨损,处于停机状态。修复前,对人员进行充分培训,确保其掌握该修复技能,操作熟练。经过5天的修复,轴颈的尺寸、精度得到恢复,确保风机可以正常运行。轴颈修复后如图3所示。
Fig. 3 Generator axle journal after repairing图3 修复后的轴颈 |
4 结论
针对风电机组发电机轴颈磨损问题,提出了一种在线镶套修复工艺,并对车削、镶套等关键工艺环节进行了计算分析。研究表明,采用该修复工艺可以保证轴颈修复后的质量,进而满足风电机组的运行要求。该技术有望在风电机组尤其是海上风电机组的发电机轴颈磨损修复方面实现推广。
符号表
P 发电机功率,kW
n 轴颈的转速,r/min
T 轴颈传递的扭矩,N∙m
γ 泊松比,无量纲
[σ] 屈服应力,MPa
τmax 轴颈的最大切应力
[τ] 轴颈的许用应力
E 弹性模量,MPa
α 线膨胀系数,1/℃
D 轴颈出厂直径,mm
l 轴颈长度,mm
Df 车削后轴颈的直径,mm
Wp 轴颈的扭转截面系数,mm3
d1 轴套的内径,mm
d2 轴套的外径,mm
qa 轴套的轴径比,无量纲
Δd 镶套后轴套的外径变化量,mm
Ci 轴颈的拉梅系数,无量纲
Ca 轴套的拉梅系数,无量纲
p min 轴颈与轴套的最小结合压力,MPa
pi max 轴颈的最大结合压力,MPa
pa max 轴套的最大结合压力,MPa
pmax 轴颈与轴套的最大结合压力,MPa
p 轴颈与轴套的实际结合压力,MPa
ei min 轴颈的最小直径变化,mm
ei max 轴颈的最大直径变化,mm
ea min 轴套的最小直径变化,mm
ea max 轴套的最大直径变化,mm
δmim 轴颈与轴套的最小有效过盈量,mm
δmax 轴颈与轴套的最大有效过盈量,mm
δ 轴颈与轴套的实际过盈量,mm
δ0 加热后的间隙量,mm
Δt 安装时轴套的加热温升,℃
ΔDf 最大车削误差
