0 引言
近年来,随着能源供给形势及化石能源带来的环境问题日益严峻,地热能开发利用受到了越来越多的关注。与太阳能和风能相比,地热能具有稳定、连续的特点,利用系数达70%以上,更适合作为基础负荷[1]。因此,加快开发利用地热能对构建清洁低碳能源体系、落实双碳战略具有重要意义。
地热资源按埋深可划分为浅层地热、中深层地热及干热岩三种类型[2],其中中深层地热利用以水热型资源为主,其具有不受地面气候影响、开发难度适中等优点,潜力巨大[3]。水热型中深层地热资源的利用方式包括发电与供热两种,其中尤以建筑采暖利用居多;截至2019年底,我国北方地区水热型地热采暖面积累计已达约2.82亿m2[4]。虽然水热型中深层地热供暖已取得了一定的成功,但目前大多数地热供暖系统对地热水的有效利用温度差较小,尾水排放温度过高（一般在40℃以上[5]）,造成地热资源利用率低,供暖能力小[6]。在常规水热型中深层地热供暖系统中引入水源热泵机组构建地热梯级供暖系统可以有效解决上述问题,且已成为当前地热供暖领域的一个重要发展方向。
国内外研究人员针对水热型中深层地热梯级供暖系统开展了大量的研究工作。如WU等[7]讨论了四种不同的热泵在地热梯级供暖系统中的应用潜力,结果表明吸收压缩式热泵性能最优;ZHENG等[8]对地热梯级供暖系统的运行策略进行优化,指出与燃煤供暖系统相比,最优策略下系统可以节约75.1%的标煤;邹平华等[9]分析了利用板式换热器与热泵机组联合供暖的设计和运行情况,并对比分析了两种优化方案;董君永等[10]探讨了采用热泵技术梯级利用地热资源进行城市集中供暖的可行模式。总体而言,现有关于水热型中深层地热梯级供暖系统的研究重点集中在地面系统的设计、运行方面,而未考虑地下热储特征对地热供暖系统性能的影响,割裂了地热供暖系统的整体性。此外,环境效益也是当前地热开发利用的关注点之一[11,12,13],但目前关于水热型中深层地热梯级供暖系统环境效益的研究工作尚不多见。
针对水热型中深层地热梯级供暖系统,建立包括地下热储和地面设备的整体系统数学模型,从全生命周期角度分析井距、井深、回灌温度及地热水流量四种参数对系统经济性和环境效益的影响,并基于遗传算法对系统进行多目标优化,以期为地热供暖系统的优化设计提供技术支撑。
1 地热梯级供暖系统
地热梯级供暖系统主要由地下和地上两部分组成,其中地下部分包括热储与井筒,地上部分为换热站,包括板式换热器（板换）与热泵机组,如图1所示。来自开采井的地热水首先进入一级板换与末端二次水进行换热,直接供末端用户使用;随后,地热水进入二级板换进行换热,将热量传递给热泵机组,经热泵机组升温后将热量传递给末端二次水,从而实现地热梯级利用;经过两级换热后的地热水直接回灌至地下。
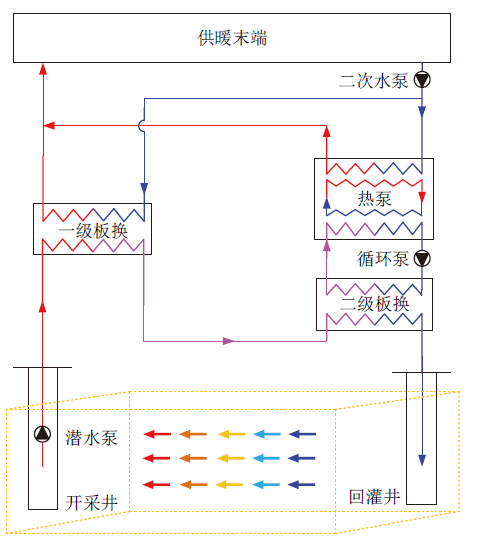
Fig. 1 Geothermal cascade heating system图1 地热梯级供暖系统 |
2 数值模型
为了简化计算,作如下假设：①系统处于稳定流动状态;②热储内裂隙呈水平状且沿竖直方向等间距分布;③地热水循环始终为单相液体流动且物性按纯水计算;④地层温度按线性变化且地温梯度已知;⑤忽略围岩的渗透性（裂隙的渗透率远远大于围岩的渗透率）;⑥不计地面系统散热损失。
2.1 井筒和热储
井筒与热储耦合（井储耦合）模型如图2所示,采用“一采一灌”对井注采模式,对井间距为L,井深为H,井筒内外径分别为ri和ro,热储厚度为D,裂隙高度为b,相邻裂隙间距为2d。
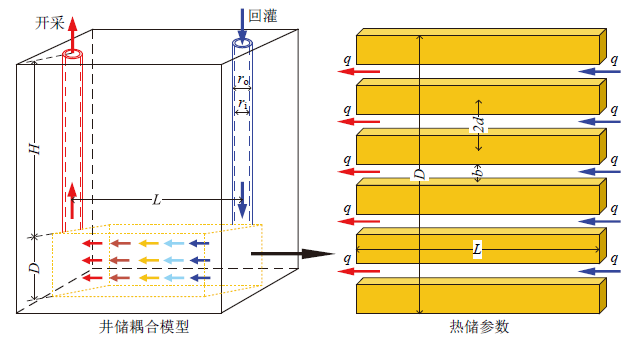
Fig. 2 Wellbore-reservoir coupled model and reservoir parameters图2 井筒与热储耦合模型及热储参数 |
在上述假设基础上,定义无量纲温度${{T}_{\text{D}}}$：
${{T}_{\text{D}}}=\frac{{{T}_{\text{f}}}-{{T}_{0}}}{{{T}_{\text{inj,b}}}-{{T}_{0}}}$ (1)
${{T}_{\text{D}}}=\frac{1}{p}\exp \left\{ \frac{\left[ \theta p+2\sqrt{p}\tanh \left( \sqrt{p} \right) \right]\xi }{2+\theta } \right\}$ (2)
其中
$\theta =\frac{{{\rho }_{\text{f}}}{{c}_{p\text{,f}}}b}{{{\rho }_{\text{r}}}{{c}_{p\text{,r}}}d}$ (3)
${{\rho }_{\text{f}}}{{c}_{p\text{,f}}}=\eta {{\rho }_{\text{w}}}{{c}_{p,\text{w}}}+\left( 1-\eta \right){{\rho }_{\text{r}}}{{c}_{p\text{,r}}}$ (4)
$b={{\left( \frac{12\tau \mu }{{{\rho }_{\text{w}}}gN} \right)}^{\frac{1}{3}}}$ (5)
$d=\frac{D}{N}$ (6)
$\xi =\frac{{{k}_{\text{r}}}\text{ }\!\!\pi\!\!\text{ }{{r}^{\text{2}}}\left( 2+\theta \right)}{{{\rho }_{\text{w}}}{{c}_{p\text{,w}}}qd}$ (7)
对于单相液体流动,可以采用RAMEY[16]提出的井筒传热模型计算生产井与回灌井内地热水温度。以回灌井为例,在稳态传热条件下,t时刻井筒任一微元段出口地热流体温度计算如下：
$T\left( z,t \right)=\omega z+{{T}_{\text{r}}}-\omega A+\left( {{T}_{\text{inj}}}+\omega A-{{T}_{\text{r}}} \right)\text{exp}\left( -\frac{z}{A} \right)$ (8)
其中
$A=\frac{{{m}_{\text{w}}}{{c}_{p\text{,w}}}\left( {{k}_{\text{r}}}+{{r}_{\text{i}}}Uf \right)}{2\text{ }\!\!\pi\!\!\text{ }{{r}_{\text{i}}}U{{k}_{\text{r}}}}$ (9)
$f=-\ln \frac{{{r}_{\text{o}}}}{2\sqrt{\alpha t}}-0.29$ (10)
$\frac{1}{U}=\frac{1}{{{h}_{\text{w}}}}+\frac{{{r}_{\text{o}}}-{{r}_{\text{i}}}}{{{k}_{\text{well}}}}$ (11)
2.2 板式换热器与热泵机组
对于板换,根据热平衡方程有下式成立：
$\begin{align} & {{Q}_{\text{HX,pri/sec}}}={{m}_{\text{geo}}}{{c}_{p\text{,w}}}\left( {{T}_{\text{geo,in}}}-{{T}_{\text{geo,out}}} \right) \\ & ={{m}_{\operatorname{sw}}}{{c}_{p\text{,sw}}}\left( {{T}_{\text{sw,out}}}-{{T}_{\text{sw,in}}} \right) \\ \end{align}$ (12)
${{T}_{\text{geo,out}}}={{T}_{\text{sw,in}}}+\Delta {{T}_{\text{pp}}}$ (13)
基于传热方程,板式换热器传热面积计算如下：
${{A}_{\text{HX}}}=\frac{{{Q}_{\text{HX}}}}{{{U}_{\text{HX}}}\Delta {{T}_{\text{HX}}}}$ (14)
对于热泵机组,其制热性能系数（coefficient of performance, COP）、蒸发器热负荷、冷凝器热负荷（即制热功率）及压缩机耗功分别计算如下[8]：
$\begin{align} & {{\varepsilon }_{\text{COP}}}=0.00605{{\left( {{T}_{\text{con,w,out}}}-{{T}_{\text{eva,w,out}}} \right)}^{2}} \\ & -0.511\left( {{T}_{\text{con,w,out}}}-{{T}_{\text{eva,w,out}}} \right)+15.48 \\ \end{align}$ (15)
${{Q}_{\text{eva}}}={{Q}_{\text{HX,sec}}}$ (16)
${{Q}_{\text{HP}}}\text{=}\frac{{{\varepsilon }_{\text{COP}}}}{{{\varepsilon }_{\text{COP}}}-1}{{Q}_{\text{eva}}}$ (17)
${{W}_{\text{com}}}\text{= }{{Q}_{\text{HP}}}-{{Q}_{\text{eva}}}$ (18)
2.3 评价指标
2.3.1 平准化供热成本
平准化供热成本（levelized cost of heat, LCOH）是一种从全生命周期视角,考虑资金的时间价值对能源系统的经济性进行评价的方法。地热供暖系统的平准化供热成本计算公式为[17]：
${{\varphi }_{\text{LCOH}}}=\frac{{{C}_{\text{TCI}}}+\sum\nolimits_{t=1}^{n}{\frac{{{C}_{\text{OM,}t}}}{{{\left( 1+i \right)}^{t}}}}}{\sum\nolimits_{t=1}^{n}{\frac{{{E}_{t}}}{{{\left( 1+i \right)}^{t}}}}}$ (19)
地热供暖系统的初投资主要包括地热井与地面换热站两部分费用,计算如下：
${{C}_{\text{TCI}}}=\left( 1+\beta \right)\left( H{{P}_{\text{well}}}\text{+}{{A}_{\text{HX,pri}}}{{P}_{\text{HX}}}+{{A}_{\text{HX,sec}}}{{P}_{\text{HX}}}\text{+}{{Q}_{\text{HP}}}{{P}_{\text{HP}}} \right)$(20)
地热供暖系统年运行维护费用主要包括设备维护费用、人工费用、电费与地热水资源费,计算如下：
${{C}_{\text{OM}}}=\gamma {{C}_{\text{TCI}}}\text{+}{{N}_{\text{per}}}{{S}_{\text{per}}}\text{+}{{E}_{\text{ele}}}{{P}_{\text{ele}}}\text{+}{{M}_{\text{geo}}}{{P}_{\text{geo}}}$ (21)
2.3.2 污染物减排量
用污染物减排量（amount of emission reduction, AOER）来表征地热供暖系统的环境效益。以燃煤供暖系统为参考,根据FAN等[18]的研究,地热供暖系统污染物包括CO2、SO2与NOx减排量计算如下：
${{\chi }_{\text{AOER}}}=82.58\times 0.0036\times \sum\nolimits_{t=1}^{n}{{{E}_{t}}}$ (22)
3 结果与讨论
Table 1 Input parameters of simulation model表1 模型输入参数 |
| 参数 | 取值 |
|---|---|
| 地热水流量 / (m3/h) | 100（50 ~ 150） |
| 回灌温度 / ℃ | 20（14 ~ 30） |
| 地热井深度 / m | 1 500（1 000 ~ 2 000） |
| 井距 / m | 200（200 ~ 1 000） |
| 井筒内径 / m | 0.244 5 |
| 井筒外径 / m | 0.311 1 |
| 热储厚度 / m | 400 |
| 岩石导热系数 / [W/(m∙℃)] | 4 |
| 岩石密度 / (kg/m3) | 2 835 |
| 裂隙数量 / 条 | 3 |
| 裂隙孔隙率 / % | 10 |
| 导水系数 / (m2/s) | 0.002 |
| 水的密度 / (kg/m3) | 1 000 |
| 水的定压比热容 / [J/(kg∙℃)] | 4 180 |
| 地温梯度 / (℃/m) | 0.05 |
| 附加费用系数 | 1.0 |
| 钻井价格 / (元/m) | 3 827 |
| 板换价格 / (元/m2) | 1 500 |
| 热泵价格 / [元/(kW∙t)] | 250 |
| 设备维护费用系数 | 0.02 |
| 运行人员数量 / 人 | 5 |
| 运行人员工资 / (元/月) | 4 000 |
| 电价 / [元/(kW∙h)] | 0.8 |
| 地热水资源价格 / (元/t) | 2.0 |
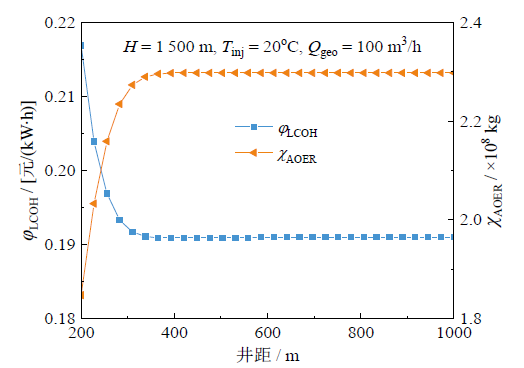
3.1 井距的影响
井距对地热供暖系统${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响如图3所示。从图中可见,在小井距情况下,随着井距的增大,地热供暖系统${{\varphi }_{\text{LCOH}}}$和${{\chi }_{\text{AOER}}}$分别呈急剧下降与上升趋势,且变化幅度逐渐减小,至井距约400 m时趋于稳定。主要原因在于,井距越小,回灌井冷锋前缘越容易到达开采井井底,导致井口温度降低,地热供热量减小,而一旦井距保持在临界距离之上,地热供热量将几乎不受井距影响而保持稳定,故系统${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$也将保持不变。
Fig. 3 ${{\varphi }_{\text{LCOH}}}$ and ${{\chi }_{\text{AOER}}}$versus well spacing图3 井距对${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响 |
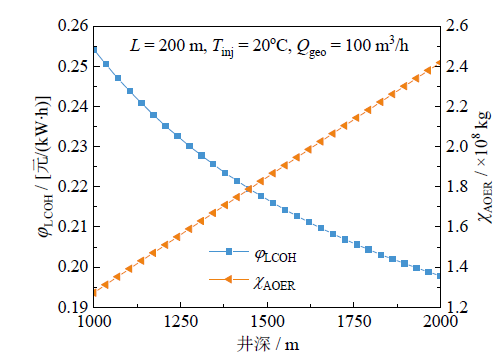
3.2 井深的影响
地热井深度对地热供暖系统${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响如图4所示。
Fig. 4 ${{\varphi }_{\text{LCOH}}}$ and ${{\chi }_{\text{AOER}}}$versus well depth图4 井深对${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响 |
从图4中可见,随着井深增大,地热供暖系统的${{\varphi }_{\text{LCOH}}}$逐渐下降,且降幅有所减缓,而${{\chi }_{\text{AOER}}}$几乎呈直线上升趋势。主要原因在于,深部储层温度更高,加大井深能够有效提高地热供热量,因此${{\varphi }_{\text{LCOH}}}$随井深增大而减小,${{\chi }_{\text{AOER}}}$随井深增大而不断提高;但增加井深会造成钻井费用升高,系统初投资上升,因此${{\varphi }_{\text{LCOH}}}$随井深增大而降低的幅度受限,曲线逐渐趋于平缓。
3.3 回灌温度的影响
回灌温度对地热供暖系统${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响如图5所示。从图中可见,随着回灌温度升高,地热供暖系统${{\varphi }_{\text{LCOH}}}$呈先减小后增大的趋势,而${{\chi }_{\text{AOER}}}$则线性下降,即存在经济回灌温度使得地热供暖系统的${{\varphi }_{\text{LCOH}}}$最小,在给定工况下,经济回灌温度约24.5℃。主要原因在于,回灌温度升高导致地热水有效利用温差减小,地热供热量随之降低,同时利用温差减小意味着地面设备的初投资成本降低,二者相互作用使${{\varphi }_{\text{LCOH}}}$呈先减小后增大趋势而${{\chi }_{\text{AOER}}}$直线下降。
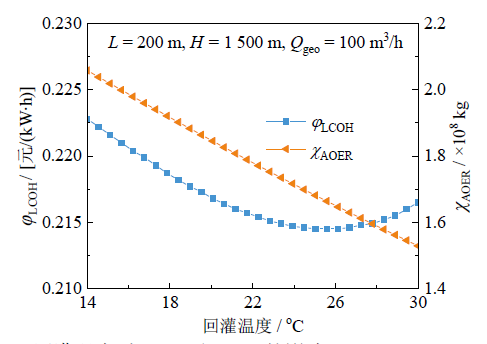
Fig. 5 ${{\varphi }_{\text{LCOH}}}$ and ${{\chi }_{\text{AOER}}}$versus reinjection temperature图5 回灌温度对${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响 |
3.4 地热水流量的影响
地热水流量对地热供暖系统${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响如图6所示。从图中可见,小流量下地热供暖系统经济性较差,而随着流量增大,地热供暖系统${{\varphi }_{\text{LCOH}}}$和${{\chi }_{\text{AOER}}}$分别下降和升高,变化幅度均逐渐减小。地热水流量小,热提取率低,供热量有限,故${{\varphi }_{\text{LCOH}}}$较大,在一定范围内加大流量供热量相应增加,但流量增大会造成回灌井冷锋前缘向开采井移动,导致开采井井口温度下降。另外增大地热水流量会造成潜水泵电耗增加,相应运行费用的上升亦是导致${{\varphi }_{\text{LCOH}}}$降幅逐渐减小的原因之一。
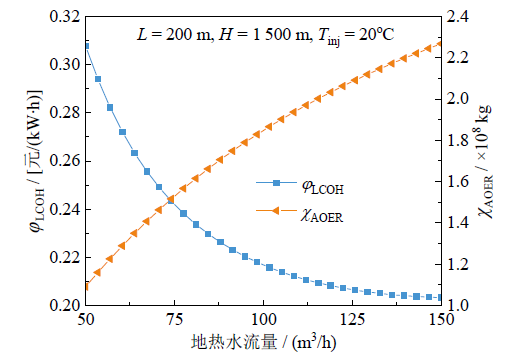
Fig. 6 ${{\varphi }_{\text{LCOH}}}$ and ${{\chi }_{\text{AOER}}}$versus geothermal water mass flow rate图6 地热水流量对${{\varphi }_{\text{LCOH}}}$及${{\chi }_{\text{AOER}}}$的影响 |
3.5 多目标优化
综合考虑经济性和环境效益,以井距、井深、回灌温度和地热水流量作为决策变量,${{\varphi }_{\text{LCOH}}}$和${{\chi }_{\text{AOER}}}$作为目标函数,则地热梯级供暖系统的优化问题可描述为：
$\left\{ \begin{align} & \min {{\varphi }_{\text{LCOH}}} \\ & \max {{\chi }_{\text{AOER}}} \\ & \text{s}\text{.t}\text{. 200}\le L\le 1 000, \\ & \text{ 1} \text{000}\le H\le 2 000\text{, } \\ & \text{ 14}\le {{T}_{\text{inj}}}\le 30\text{,} \\ & \text{ 50}\le {{Q}_{\text{geo}}}\le 150 \\ \end{align} \right.$ (23)
多目标优化的结果是一组Pareto解集,利用模糊集决策方法从该解集中获取最优折衷解,具体计算方法见参考文献[20]。
利用遗传算法获得的多目标优化Pareto最优前沿解集如图7所示。图中,X点为${{\varphi }_{\text{LCOH}}}$最优点,该点系统的经济性最好;Y点为${{\chi }_{\text{AOER}}}$最优点,该点系统的环境效益最佳;Z点为决策出的最优折衷解（经济性和环境效益同等重要）,该点系统的经济性和环境效益同时达到理想最佳。从图中可以看出,随着系统${{\varphi }_{\text{LCOH}}}$的增大,${{\chi }_{\text{AOER}}}$呈上升趋势。从表2可以看出,当经济性和环境效益同时达到最优时,地热供暖系统的${{\varphi }_{\text{LCOH}}}$约为0.14元/(kW∙h),${{\chi }_{\text{AOER}}}$约为4.17 × 108 kg。最优解对应的决策变量值如表3所示,其中最优井距为668.11 m、井深为1 929.96 m、回灌温度为24.01℃、地热水流量为149.96 m3/h。
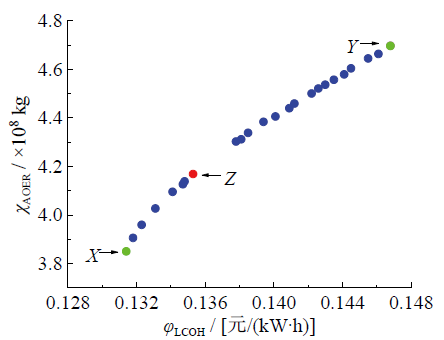
Fig. 7 Pareto optimal solutions of multi-objective optimization图7 多目标优化Pareto最优前沿 |
Table 2 Objective values of optimal solutions in the Pareto frontier表2 Pareto最优解的目标值 |
| 最优解 | 目标值 | |
|---|---|---|
| ${{\varphi }_{\text{LCOH}}}$/ (元/kW∙h) | ${{\chi }_{\text{AOER}}}$/ ×108 kg | |
| X | 0.13 | 3.85 |
| Y | 0.15 | 4.70 |
| Z | 0.14 | 4.17 |
Table 3 Data setting for decision variables of optimal solutions in the Pareto frontier表3 Pareto最优解的目标值对应的决策变量取值 |
| 最优解 | 决策变量 | |||
|---|---|---|---|---|
| 井距 / m | 井深 / m | 回灌温度 / ℃ | 地热水流量 / (m3/h) | |
| X | 666.98 | 1 932.07 | 29.88 | 150.00 |
| Y | 668.89 | 1 929.83 | 15.20 | 149.96 |
| Z | 668.11 | 1 929.96 | 24.01 | 149.96 |
4 总结
分析了井距、井深、回灌温度及地热水流量四个参数对考虑热储特征的地热梯级供暖系统经济性与环境效益的影响,并基于遗传算法对系统进行了多目标优化,得出如下结论：
（1）采灌井之间存在一个临界距离,井距在临界值以上时系统的${{\varphi }_{\text{LCOH}}}$与${{\chi }_{\text{AOER}}}$在寿命期内几乎不受井距影响,因此地热供暖系统设计时应保证井距在临界值以上。
（2）井深不仅影响储层产热能力,同时决定钻井费用,深井地热供暖系统供热量大但初投资较高,开发利用前需对地热资源进行详尽勘探,既要保证储层产热能力,又需减小钻井深度,降低钻井费用。
（3）存在一个经济回灌温度使得地热供暖系统${{\varphi }_{\text{LCOH}}}$最小,在给定工况范围内经济回灌温度为24.5℃,可为地热供暖系统回灌温度的确定提供思路。
（4）在一定工况范围内,随着地热水流量的增大,地热供暖系统的经济性与环境效益均越来越好,但改善幅度越来越小,因此需要结合热储特征,综合考虑经济性和环境效益来合理设计地热水流量。
（5）以${{\varphi }_{\text{LCOH}}}$最小与${{\chi }_{\text{AOER}}}$最大为目标函数,对地热供暖系统进行多目标优化设计,并通过模糊集决策方法确定了最优解决方案,该方案下系统的${{\varphi }_{\text{LCOH}}}$约为0.14元/(kW∙h),${{\chi }_{\text{AOER}}}$约为4.17 × 108 kg。
符号表：
A 松弛参数
AHX 板式换热器传热面积,m2
b 裂隙高度,m
C 费用,元
cp 比热容,J/(kg∙℃)
D 热储厚度,m
d 裂隙半间距,m
E 年供热量,kW∙h
Eele 系统耗电量,kW∙h
f 时间函数
g 重力加速度,m/s2
H 井深,m
h 对流传热系数,W/(m2∙℃)
i 折现率
k 导热系数,W/(m∙℃)
L 对井间距,m
M 采水量,t
m 质量流量,kg/s
N 裂隙数量,条
Nper 运行人员数量,人
n 系统运行寿命,年
Pwell 地热井钻井价格,元/m
PHX 板换价格,元/m2
PHP 热泵价格,元/(kW∙t)
Pele 电价,元/(kW∙h)
Pgeo 地热水资源价格,元/t
p Laplace参数
Q 热负荷,W
Qgeo 地热水流量,m3/h
q 裂隙流体体积流量,m3/s
ri 井筒内径,m
ro 井筒外径,m
Sper 运行人员工资,元/月
T 温度,℃
TD 无量纲温度
Tinj,b 回灌井井底温度,℃
T0 裂隙流体初始温度,℃
ΔT 对数平均温差,℃
ΔTpp 夹点温差,℃
U 总传热系数,W/(m2∙℃)
W 耗电功率,W
z 井筒位置,m
α 地层热扩散系数,m2/s
β 附加费用系数
γ 维护费用系数
εCOP 性能系数
η 裂隙孔隙率
θ 无量纲参数
μ 动力黏度,kg/(m∙s)
ξ 无量纲参数
ρ 密度,kg/m3
τ 导水系数,m2/s
${{\varphi }_{\text{LCOH}}}$ 平准化供热成本,元/(kW∙h)
${{\chi }_{\text{AOER}}}$ 污染物减排量,kg
ω 地温梯度,℃/m
下角标：
com 压缩机
con 冷凝器
eva 蒸发器
f 裂隙流体
geo 地热水
HX 板式换热器
HP 热泵
inj 回灌
in 进口
OM 运行维护
out 出口
pri 一级（板换）
r 岩石
sec 二级（板换）
sw 二次侧流体
TCI 初投资
w 水
well 井筒
