0 引言
在应对气候变化与实现碳达峰、碳中和目标过程中,电动汽车（electric vehicle, EV）作为一种环境友好型交通工具,近年来在全球范围内得到大力推广。EV作为一种可移动储荷资源,有别于电力系统中其他常规负荷,不仅能在电力系统任意节点充电,还能通过车网互动（vehicle to grid, V2G）技术向系统中的节点进行反向馈电。截至2021年底,全球道路上拥有1 000万辆EV,且EV保有量继续呈逐年攀升趋势。预计2025年将达到5 000万辆,届时EV可向电网提供的最大容量达到600 GW[1]。EV的大规模发展在促进减碳减排的同时,也使得电力系统的运行面临着巨大挑战[2]。V2G调度策略通过研究EV的时空特性,进一步挖掘EV移动储荷资源,从而支撑电网进行移峰填谷,提高可再生能源消纳比例。因此,合理引导EV在特定时空下参与V2G调度,以及开展V2G调度策略下多指标评估分析具有重要的现实意义。
目前,V2G的理论技术研究已经有大量丰富的研究成果[3],尤其在调度技术上对V2G的调度策略研究方面。ANTÚNEZ等[4]提出一种基于混合整数线性规划的方法来求解考虑V2G技术的非平衡配电系统中EV的最优充电协调问题。SCARABAGGIO 等[5]提出两种控制策略来实现EV蓄电池在频率调节过程中的最优控制。为弥补大规模EV接入调度产生的各层级信息断层与延迟问题,采用多层级调度策略来提高EV集群的响应速度,最大化利用EV的储荷资源[6,7,8]。文献[9,10,11]通过研究EV的时空活动特性,分析EV与EV集群的需求响应潜力。文献[12,13,14]以充分消纳吸收可再生能源为目标,研究V2G调度策略实现方法,充分利用EV的移动储荷资源提高多方参与主体的经济性。文献[15,16]研究采用动态的可再生能源电价取代现有的固定充放电价格模式,采用V2G策略消纳更多的可再生能源,提高可再生能源利用率,增加了社会的经济效益。NEYESTANI等[17]建立一种基于城市EV不确定性的混合整数规划V2G调度模型,该模型验证在适当的定价方案下可以使得多方获得更高的利润。以上工作聚焦在技术层面对V2G调度进行研究,通过V2G调度充分利用EV集群资源实现电网负荷的波动小、可再生能源消纳多、社会经济效益佳等效果,然而均未对调度效果进行评估。
在可再生能源高渗透的背景下,基于时间序列方向矩阵,LIU等[18]提出二分法嵌入式粒子群优化算法,充分利用EV储荷特性消纳尽可能多的可再生能源,该方法同时对调度效果进行评估,指导V2G调度策略闭环优化,提高了区域系统内能源的自给率。文献[19,20]提出“可调度能力”概念,建立了以配电网总负荷峰谷差最小化为指标的EV可调度能力分析模型。张亚朋等[21]以大规模EV构成的虚拟电厂（electric vehicle virtual power plant, EVPP）为分析对象,提出一种多时间尺度响应能力评估模型,该模型能评估日前响应能力并指导修正调控策略。WEI等[22]提出了一种基于改进的NSGA-II算法,对V2G与综合能源系统（integrated energy systems, IES）耦合作为灵活存储的可行性的评估方法,主要评估经济和环境效益,评估结果准确地描述V2G与IES耦合的可行性。TAN等[23]对风-光电-水电混合动力系统互补运行的效益和风险进行评估,通过量化不确定性风险指标来建立可靠性指数,对可靠性进行评估。以上文献在优化调度评估方面已有深入的研究,但是在EV V2G的可靠性和经济性评估方面还未形成体系,缺少从多个指标对V2G调度策略效果进行评估,无法为调度决策者提供全面的信息。
针对V2G调度策略执行后的效果,提出一种多指标评估模型,从电网和用户的角度,围绕可再生能源消纳比率、可调度容量、调度响应时间、负荷平稳度和调度运行经济效益共五个指标来评估调度策略运行效果。该模型可以分析在相同的情景条件下运行不同的调度策略,直观地展示V2G调度策略在不同指标上的表现。为调度系统优化、调度策略选型等提供依据和指导,提升调度决策全面性和可靠性,促进调度理想度水平的提升。
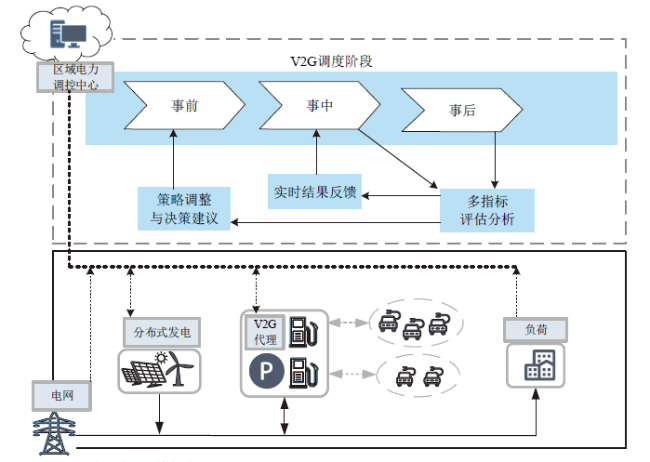
1 V2G调度系统的多指标评估框架
V2G调度系统由V2G充放电桩、电力负荷、可再生能源发电设备与传统发电机组设备组成,所有系统组成单元均通过信息流和能量流双向流通,实时交互。信息流包含V2G调度中心与分布式发电、充电桩运营商、电力负荷以及EV之间的双向交流。能量流包含电网与充电桩、充电桩与EV之间的能量双向流通。
Fig. 1 The multi-index evaluation framework for V2G dispatch system图1 面向V2G调度系统的多指标评估框架 |
V2G调度中心包含整个调度过程中的事前、事中及事后所有数据,其中事前对系统数据进行预处理,模拟策略执行过程,得到事中数据。根据事中数据对调度策略进行反馈,最后获得事后调度结果。对调度整个过程进行多指标评估,与调度策略的预期目标进行对比分析,闭环调整调度策略参数,使得模拟调度结果达到调度策略的期望。
2 V2G调度模型
2.1 目标函数
在V2G调度系统中,日前、日内的V2G调度模型重点考虑EV用户出行距离、出行起止时间等出行需求以及电池类型、容量、单位里程能耗等车辆特性参数。V2G调度可以充分有效调度规模化EV的移动储荷资源进行充放电,使得系统达到预期的运行目标,如平衡电网负荷波动、提升可再生能源消纳比例和最大化调度运行经济效益等。基于前期研究提出的V2G经济调度模型及多级车网优化调度方法[26],调整不同场景下V2G调度参数与策略目标方程,以实现各策略之间的择优。
V2G日前调度模型约束条件组包括EV服务约束、并网功率约束和电力系统平衡约束。
2.2 EV服务约束
Table 1 V2G system parameters表1 V2G系统特征常量参数表 |
| 用户变量名 | 变量说明 |
|---|---|
| ${{C}_{i}}$ | 存储电量的能力 |
| $S_{i}^{\text{u,}\max }$ | EVi用户允许电池最大荷电状态 |
| $S_{i}^{\text{u,}\min }$ | EVi用户允许电池最小荷电状态 |
| $S_{i}^{\text{u,end}}$ | EVi用户离开时要求最小荷电状态 |
| $T_{i}^{\text{start}}$ | EVi开始V2G的时间 |
| $T_{i}^{\text{stop}}$ | EVi离开V2G的时间 |
| $P_{i}^{\text{ev}}$ | EVi允许的最大充放电功率 |
| $P_{m}^{\text{s}}$ | 充电桩额定充放电功率 |
| $\eta _{i}^{\text{ev}}$ | EVi充放电效率 |
Table 2 V2G system variables表2 V2G系统特征变量表 |
| 变量名 | 变量说明 |
|---|---|
| ${{s}_{i,t}}$ | EVi在t时刻的荷电状态 |
| $\mu _{i,t}^{\text{c}}$ | EVi在t时刻的充电状态 |
| $\mu _{i,t}^{\text{d}}$ | EVi在t时刻的放电状态 |
| $p_{i,t}^{\text{c}}$ | EVi在t时刻的充电功率 |
| $p_{i,t}^{\text{d}}$ | EVi在t时刻的放电功率 |
以 |I| 辆EV组成的EV集群中第i辆车EVi为例,其存储电量能力为${{C}_{i}}$电池存储容量比例（state of charge, SOC）上限为$S_{i}^{\text{u,m}ax}$,SOC允许下限为$S_{i}^{\text{u,}\min }$;接入电网参与V2G的起始时间为$T_{i}^{\text{start}}$,离网时间为$T_{i}^{\text{stop}}$,在线时间区间$\left[ T_{i}^{\text{start}},T_{i}^{\text{stop}} \right]$。EVi并网时段内响应调度中心发送的充电、放电、空闲（不充不放）等V2G调度指令。此外,为保证车主的用车需求,在EVi离网时需确保SOC不低于用户期望值$S_{i}^{\text{u,end}}$,为保证EVi电池安全,EVi最大充放电功率不能超过$P_{i}^{\text{ev}}$。EVi响应V2G调度指令时其服务状态与SOC变化区间如图2所示。
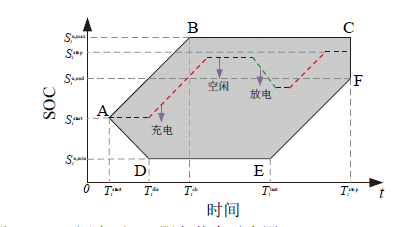
Fig. 2 EV service status in V2G scheduling图2 V2G调度下EV服务状态示意图 |
所有响应V2G的服务车辆在并网时段内$\forall i\in I$、$\forall t\in [T_{i}^{\text{start}},T_{i}^{\text{stop}}]$,即EV在线响应V2G调度时有约束条件式（1）~ 式（6）：
$\mu _{i,t}^{\text{c}}+\mu _{i,t}^{\text{d}}\le 1$ (1)
$p_{i,t}^{\text{c}}\le P_{i}^{\text{ev}}$ (2)
$p_{i,t}^{\text{d}}\le P_{i}^{\text{ev}}$ (3)
${{C}_{i}}\times {{s}_{i,t}}={{C}_{i}}\times {{s}_{i,t-1}}+p_{i,t}^{\text{c}}\times \eta _{i}^{\text{ev}}-\frac{p_{i,t}^{\text{d}}}{\eta _{i}^{\text{ev}}}$ (4)
$S_{i}^{\text{u},\min }\le {{s}_{i,t}},\forall t\in T\ \ \forall i\in I$ (5)
$S_{i}^{\text{u,end}}\le {{s}_{i,t}},\forall t=T_{i}^{\text{stop}}$ (6)
2.3 EV并网功率约束
V2G系统调度中心根据EV的活动区域,将EVi分配至其期望的服务区域内的充电桩为m,EVi的响应功率不仅受限于自身充放电功率$P_{i}^{\text{ev}}$与当前可调度容量${{C}_{i}}\cdot {{s}_{i,t}}$,还受限于充电桩额定充放电功率$P_{m}^{\text{s}}$。此时EVi参与V2G响应功率约束为：
$p_{i,t}^{\text{c}}\le \min \left( P_{i}^{\text{ev}},\frac{{{C}_{i}}\cdot {{s}_{i,t}}}{\Delta T},P_{m}^{\text{s}} \right)$ (7)
$p_{i,t}^{\text{d}}\le \min \left[ P_{i}^{\text{ev}},\frac{{{C}_{i}}\left( 1-{{s}_{i,t}} \right)}{\Delta T},P_{m}^{\text{s}} \right]$ (8)
2.4 电力系统平衡约束
由于V2G系统可存在电力系统的源、荷、储三侧,与多个电力网络节点相连。常规负荷、常规发电设备、可再生能源发电、充放电桩等均分布在电力网络节点上,在$t,\forall t\in T$时刻,节点$n,\forall n\in N$的流入流出功率保持平衡,因此有：
$-C_{l}^{\text{line}}\le {{f}_{l,t}}\le C_{l}^{\text{line}}$ (9)
$p_{n,t}^{\text{IN}}=\sum\nolimits_{l\in A_{n}^{+}}{f_{l,t}^{\text{in}}+}p_{n,t}^{\text{g}}+p_{n,t}^{\text{r}}+\sum\nolimits_{i\in I}{p_{i,t}^{\text{d}}}$ (10)
$p_{n,t}^{\text{OUT}}=\sum\nolimits_{l\in A_{n}^{-}}{f_{l,t}^{\text{out}}+}p_{n,t}^{\text{load}}+\sum\nolimits_{i\in I}{p_{i,t}^{\text{c}}}$ (11)
$p_{n,t}^{\text{IN}}=p_{n,t}^{\text{OUT}}$ (12)
式中：$A_{n}^{+}$为流入节点n连接线集合;$A_{n}^{-}$为流出节点n连接线的集合;$C_{l}^{\text{line}}$为电力线路l两端之间能够互相流通的功率;${{f}_{l,t}}$为线路l相双向流通的流通功率,为正表示正按照标识方向流通,为负表示反向流通;$p_{n,t}^{\text{g}}$为节点n常规发电功率;$p_{n,t}^{\text{r}}$为节点n可再生能源发电功率;$p_{n,t}^{\text{load}}$为节点n常规负荷;$\sum\nolimits_{i\in I}{p_{i,t}^{\text{c}}}$为接入节点n的EV充电功率之和;$\sum\nolimits_{i\in I}{p_{i,t}^{\text{d}}}$为接入节点n的EV放电功率之和;$p_{n,t}^{\text{IN}}$为节点n在t时刻的流入功率;$p_{n,t}^{\text{OUT}}$为节点n在t时刻的流出功率。
3 多指标V2G调度策略评估方法
基于前述的V2G调度策略运行框架,EV参与V2G给电网与运营商带来的收益及影响需要从多方面判断和衡量,本文提出的V2G EV调度策略的多指标评估方法,围绕可调度容量、调度响应时间、可再生能源消纳比率、负荷平稳度和调度运行经济效益,建立五个独立指标,形成V2G调度的多指标评估模型。
首先,V2G调度中心获取区域内的EV、充电桩等物理参数特征,对EV参与V2G的初始状态、并离网要求及行驶计划进行初始化,设定调度策略的服务价格、充放电价格等参数,V2G调度中心统计接受邀约的车辆状态信息,然后确定V2G调度优化目标,更新车辆充放电节点、起始时间与服务时长,求解获得车辆参与V2G调度计划,并判定当前调度结果是否满足特定评估指标。若未能满足该指标,则调整V2G调度策略参数,激励改变参与V2G邀约车辆的数量、充放电容量、充放电起始时间与时长,找到满足特定指标的最佳V2G策略和车辆调度计划。V2G调度策略多指标评估流程如图3 所示。
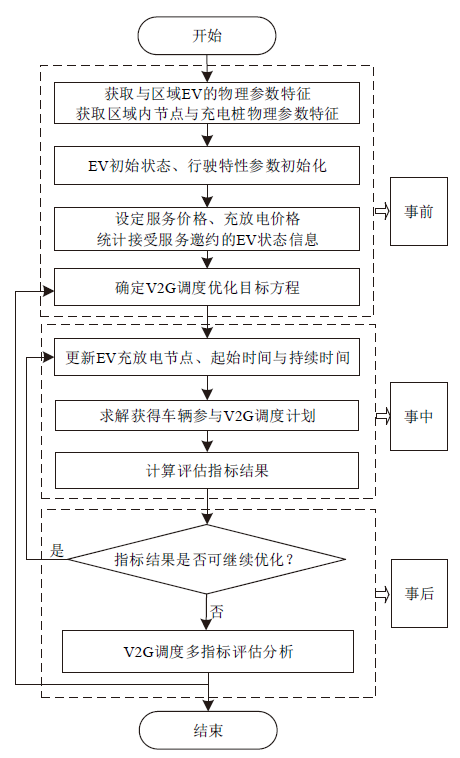
Fig. 3 Multi-index evaluation process for V2G scheduling strategy图3 V2G调度策略多指标评估流程 |
3.1 可再生能源消纳比率评估
可再生能源消纳比率表征可再生能源被电网消纳的总量与可再生能源发电总量之比。由于可再生能源发电具有惯性小、波动大等特点,规模化可再生能源并网给电网稳定运行造成安全隐患。现行可再生能源电站需根据装机容量按一定比例配置储能,EV作为移动储能单元根据调度指令在指定节点消纳可再生能源。定义V2G调度系统中可再生能源消纳比率${{\beta }^{\text{re}}}$,则有：
${{\beta }^{\text{re}}}=\frac{{{p}^{\text{rc}}}}{{{p}^{\text{gr}}}}$ (13)
式中：${{p}^{\text{rc}}}$为再生能源实际消纳量;${{p}^{\text{gr}}}$为可再生能源出力能力。
3.2 EV可调度容量评估
EV可调度容量表征愿意参与调度的EV集群在满足基本出行前提下,EV集群可以参与V2G的容量。
EV在响应调度过程中,EV与充放电桩的互动功率受限制于调度指令、车辆当前容量状态、车辆额定充放电功率及充电桩额定充放电功率,如式（8）所示。系统的实际可调度容量定义为所有车辆参与V2G放电功率的总和。V2G调度系统的可调度放电容量${{Q}_{\text{d}}}(t)$计算公式见式（14）：
${{Q}_{\text{d}}}(t)=\sum\limits_{i=1}^{I}{\int_{nT}^{nT+T}{P_{i}^{\text{ev}}\times \mu _{_{i,t}}^{\text{d}}\text{d}t}}$ (14)
3.3 可再生能源消纳比率评估
EV调度响应时间表征EV接受V2G服务邀约后满足调度指令所需时间。电网负荷突然增加时,发电侧供电无法快速响应,造成发电机转速降低、电网频率降低,V2G调度利用EV集群惯性小的特点,快速响应电网调度需求。在$t,\forall t\in T$时刻,车辆集群响应时间为$\Delta \tau (t)$,则有：
$\Delta \tau (t)=\frac{\Delta {{Q}^{\text{gr}}}(t)+\Delta {{Q}^{l}}(t)}{\sum\nolimits_{m=1}^{M}{P_{m}^{\text{s}}{{f}_{m}}}}$ (15)
式中：$\Delta {{Q}^{\text{gr}}}(t)$为可再生能源发电容量波动;$\Delta {{Q}^{l}}(t)$为系统负荷需求容量波动;${{f}_{m}}$为充电桩m的充放电状态,${{f}_{m}}=1$表示充放电桩m给EV充电,${{f}_{m}}=-1$表示充放电桩m接受EV放电,${{f}_{m}}=0$表示充放电桩m的空闲状态。
3.4 EV调度负荷平稳度评估
EV调度负荷平稳度表征在车辆集群参与V2G调度下,电网的最大负荷与最小负荷的波动。考虑区域负荷本身具有峰谷特性,故当EV并网后,合理安排调度EV的充放电时序与功率,能有效减少电网负荷峰值以减轻电网运行压力,提高电网最低负荷以提升电网与能源的利用效率,降低电网负荷波动率。假定电网负荷的平稳率为${{\alpha }^{\text{g}}}$,则有：
${{\alpha }^{\text{g}}}=1-\frac{P_{\max }^{\text{load}}-P_{\min }^{\text{load}}}{P_{\max }^{\text{load}}}$ (16)
式中：$P_{\max }^{\text{load}}$为调度运行区间内的最大负荷;$P_{\min }^{\text{load}}$为调度运行区间内的最小负荷。
3.5 EV调度运行经济效益评估
EV调度运行经济效益表征在EV参与调度下,V2G系统整体经济效益。合理引导EV在时间上和空间上参与V2G调度,不仅可以降低EV无序充电对电网的冲击,还能通过移峰填谷、调峰调频,提高多方主体的经济效益。用户响应服务收益为F1,环境收益为F2,节点负荷不能满足造成的补偿为F3,电网过网费用为F4。
$F1=\sum\limits_{i=1}^{I}{\sum\limits_{t=0}^{23}{\left( p_{i,t}^{\text{d}}\cdot c_{t}^{\text{d}}-p_{i,t}^{\text{c}}\cdot c_{t}^{\text{c}} \right)}}$ (17)
$F2=\sum\limits_{i=1}^{I}{\sum\limits_{t=0}^{23}{\left( p_{i,t}^{\text{c}} \right)\lambda }}$ (18)
$F3=\sum\limits_{i=1}^{I}{\sum\limits_{t=0}^{23}{\left( p_{n,t}^{\text{node}} \right)\delta }}$ (19)
$F4=\sum\limits_{i=1}^{I}{\sum\limits_{t=0}^{23}{\left( p_{l,t}^{\text{flow}} \right)\gamma }}$ (20)
式中：$c_{t}^{\text{c}}$和$c_{t}^{\text{d}}$分别为第t时刻EV参与V2G的充放电单价;$p_{n,t}^{\text{node}}$为采用V2G调度后第n节点的整体功率。$p_{l,t}^{\text{flow}}$为采用V2G调度后第t时刻第l条线网传输的功率;$\lambda $、$\delta $和$\gamma $分别为碳减排价值系数、补偿系数和电网负荷损益比系数。
3.6 多指标评估结果标准化
V2G调度策略需从多指标中评估衡量,由于各指标间的量纲单位不同,且结果值范围不一致,难以判断各自策略的优缺点,需对评估结果进行标准化处理。
可调度容量与调度响应时间是步阶相关举证,采用云模型方法生成一个评估结果。云模型的理论基础如下：假定存在集合$Q=\{x\}$为变量x的论域。对于集合Q中任意元素x,均存在一个有稳定倾向的随机数$0\le \mu (x)\le 1$,$\mu (x)$为隶属度,论域Q上的分布称为云。采用超熵${{H}_{\text{e}}}$指标反映在论域空间中元素分部的凝聚性,其计算方法为：
${{E}_{x}}=\frac{1}{N}\sum\limits_{i=1}^{N}{{{x}_{i}}}$ (21)
${{E}_{n}}=\sqrt{\frac{\text{ }\!\!\pi\!\!\text{ }}{2}}\times \frac{1}{N}\sum\limits_{i=1}^{N}{\left| {{x}_{i}}-{{E}_{x}} \right|}$ (22)
${{S}^{2}}=\frac{1}{N-1}\sum\limits_{i=1}^{N}{{{\left( \left| {{x}_{i}}-{{E}_{x}} \right| \right)}^{2}}}$ (23)
${{H}_{\text{e}}}=\sqrt{{{S}^{2}}-{{E}_{n}}^{2}}$ (24)
针对可再生能源消纳比率、负荷平稳度和经济效益三个阶段性指标,本文标准化采用$\min -\max $,其标准化计算公式为：
${{x}_{n}}=\frac{x-{{x}_{\min }}}{{{x}_{\max }}-{{x}_{\min }}}$ (25)
4 算例分析
4.1 算例场景及参数设置
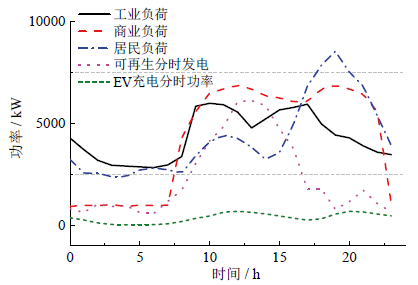
Fig. 4 Load, renewable energy generation and EVs charging daily load curve图4 负荷、可再生能源发电与EV集群充电日负荷曲线 |
该区域内充放电桩共计228个,分布在改进型的IEEE-33节点配电网的第0、7、21、24节点,EV充放电效率均为0.95。EV分布节点与节点充电桩的充/放电功率$P_{m}^{\text{s}},\forall m\in M$特性如表3所示。
Table 3 EV charging station layout and rated power表3 充电桩的分布与额定功率 |
| 分布节点 | 充电桩编号 | 充/放电额定功率 / kW |
|---|---|---|
| 0 | 0 ~ 45 | 50 |
| 7 | 46 ~ 129 | 100 |
| 21 | 130 ~ 189 | 80 |
| 24 | 190 ~ 227 | 40 |
本算例拥有1 253辆EV,将蓄电池容量${{C}_{i}}$与功率$P_{i}^{\text{ev}}$等相近特性参数归为同一类型的EV集群,结果如表4所示。
Table 4 The characteristic parameters of EV group表4 EV集群类型及特性参数 |
| 集群 类型 | 容量 / (kW∙h) | 编号 | 最大充放电功率 / kW |
|---|---|---|---|
| Ⅰ | 100 | 0 ~ 26 | 100 |
| Ⅱ | 75 | 27 ~ 550 | 50 |
| Ⅲ | 60 | 551 ~ 618 | 40 |
| Ⅳ | 50 | 619 ~ 786 | 25 |
| Ⅴ | 35 | 787 ~ 1 252 | 20 |
Table 5 Time-of-use rate for EV charging and discharging表5 EV充放电分时电价 |
| 时段 | 充电价格 / [元/(kW∙h)] | 放电价格 / [元/(kW∙h)] |
|---|---|---|
| 峰14:00-17:00、19:00-22:00 | 2.0 | 1.5 |
| 平8:00-14:00、17:00-19:00、22:00-24:00 | 1.5 | 1.0 |
| 谷0:00-8:00 | 1.0 | 0.5 |
根据文献[31]有式（18）~ 式（20）中环境价值系数$\lambda $为0.156 8元/(kW∙h),调度成本支出系数$\delta $为0.069元/(kW∙h),电网负荷损益比系数$\gamma $为0.58元/(MW∙h)2。
Table 6 V2G dispatch strategy表6 V2G调度策略 |
| 策略名称 | 策略特点 |
|---|---|
| 分时电价 | 执行域内峰谷平充放电价格 |
| 停车费减免 | EV在线时间变长,可参与V2G时间变长 |
| 可再生能源消纳 | 根据可再生能源发电量变化,动态调整充放电价格 |
Table 7 Objective function of V2G strategy表7 V2G调度策略的目标函数 |
| 策略名称 | 目标函数 | 目标 |
|---|---|---|
| 分时电价 | $\text{Max}\,F=F1+F2-F3-F4$ | 最大收益 |
| 停车费减免 | $\text{Max}\,F={{\alpha }^{\text{g}}}$ | 最大平稳度 |
| 可再生能源消纳 | $\text{Max}\,F={{\beta }^{\text{re}}}$ | 最大消纳 |
4.2 调度运行结果分析
依次对工业区区域分别执行分时电价、停车费减免、可再生能源消纳三种调度策略。得到不同场景下执行不同调度策略后系统的峰谷负荷见表8。
Table 8 Peak value of charge/discharge in three strategies and three scenarios表8 三种算例场景、三种调度策略充放电峰值 |
| 场景 | 调度策略 | EV充电峰值 / kW | EV放电峰值 / kW |
|---|---|---|---|
| 工 业 区 | 无调度 | 5 590.78 | 0.00 |
| 分时电价 | 1 924.74 | 257.08 | |
| 停车费减免 | 2 113.74 | 2 523.30 | |
| 可再生能源消纳 | 4 556.84 | 2 183.34 | |
| 商 业 区 | 无调度 | 5 590.78 | 0.00 |
| 分时电价 | 1 305.53 | 309.28 | |
| 停车费减免 | 1 833.91 | 3 679.60 | |
| 可再生能源消纳 | 2 937.02 | 1 744.91 | |
| 居 民 区 | 无调度 | 5 590.78 | 0.00 |
| 分时电价 | 1 608.89 | 1 009.56 | |
| 停车费减免 | 2 703.70 | 2 475.65 | |
| 可再生能源消纳 | 2 184.47 | 2 286.79 |
综合表8可以得到,在工业区场景中,分时电价、停车费减免和可再生能源消纳调度策略的EV峰值充电功率分别降低65.5%、62.2%、18.5%;商业区场景中的调度策略EV的峰值充电功率分别降低76.6%、67.2%、47.5%;居民区场景的调度策略EV的峰值充电功率分别降低71.2%、51.6%、60.9%。同时发现,停车费减免调度策略能显著提升EV车主参与V2G的积极性,使峰值放电功率也相对更高,该策略尤适用于工业区和商业区。
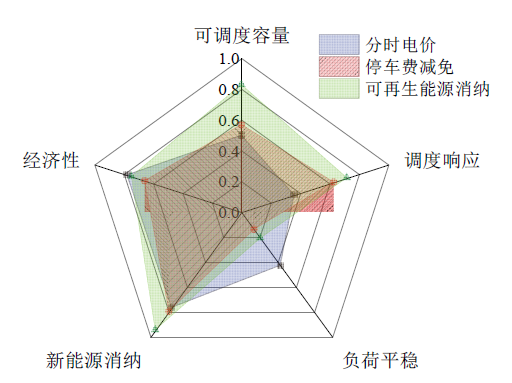
4.3 多指标评估结果分析
对工业区分别执行分时电价、停车费减免、可再生能源消纳三种调度策略的结果进行多指标评估,评估结果如图5所示。
Fig. 5 Evaluation results of different scheduling strategies in the industrial scenario图5 工业区场景下运行不同的调度策略的评估结果 |
由评估结果可以看出,在工业园区场景中,分时电价的V2G调度策略在可再生能源消纳比率、可调度容量、调度响应时间、负荷平稳度和调度运行经济效益五个指标表现均衡。若提高工业园区V2G系统的可调度容量与缩短响应时间,则需对V2G调度模型的容量约束条件以及响应车辆规模进行调整。通过停车费减免和可再生能源消纳,V2G调度系统的可调度容量与响应时间指标均能显著提高。由于更多的EV参与V2G并网,在短时间总体负荷改变较大,重点影响了电网运行过程中的负荷平稳度,同时降低运行的经济效益。
在商业区场景中,三种策略下新能源消纳指标无显著差异,新能源发电高峰时段与商业区用电高峰时段无重叠,新能源发电能被日常运营消纳。分时电价策略较其他两种策略具有更高经济效益,但在响应时长和调度容量方面不及停车费减免策略。而停车费减免策略更适用于商业区,确保调度过程拥有更多EV可调度容量和更长服务时长,满足调峰调频任务的执行。
在居民区场景中,由于大多数车主停车都是刚性需求,通过停车费减免策略可以激发车主参与V2G的意愿,增大车辆并网概率,增加可调度容量。此外,峰谷时段负荷差异明显,分时电价和停车费减免策略均能获得较佳的经济效益。
5 结论
对调度策略的闭环管控是提高调度成效的重要手段。为此,首先分析了EV V2G调度策略的目标方程和边界约束,提出多指标评估方法和流程。选取某市区的工业区、商业区、居民生活区三个典型应用场景,分别基于分时电价、停车费用减免、可再生能源消纳的三种EV调度V2G优化调度策略进行仿真对比分析,得出以下结论：
（1）在相同场景下,调度策略在不同指标下的表现结果不同,通过对调度策略的边界约束进行调整,可以提升V2G调度系统目标指标的调度结果,如在工业区使用分时电价调度策略,在可调度容量与调度响应指标上表现不理想,通过停车费减免V2G调度措施,能够增加EV的车网互动响应时长,从而使V2G调度系统整体调度容量提高66%。
（2）同一种调度策略应用在不同场景,其调度评估指标结果不尽相同。如分时电价调度策略在商业区具有很好的经济性,可以达到96%,但是在居民区,由于居民的刚性负荷需求,其经济效益只有70%。因此调度策略调整需要结合应用场景的用能特点。
算例分析结果表明,提出的V2G调度策略多指标方法能够实现调度策略的优化和改进,但同时也发现,不同主体间的利益对系统的运行结果影响较大,后续为了更好地应用本评估模型,需挖掘和发现影响V2G调度效果的其他因子,在满足用户出行需求与电网运行平稳的同时,最大限度提高社会效应与多方的经济效益。
