0 引言
在混合气体燃烧之前,需要系统地研究可燃混合物的层流火焰特性,包括层流燃烧速度（laminar burning velocity, LBV）和火焰不稳定性,这对理解燃料-氧化剂混合物的燃烧机理非常重要[3]。因此,为了改进氢气-乙醇反应机理和验证数值模拟,需要进一步的实验工作来丰富数据库。现有文献广泛报道了关于添加H2的可燃混合物LBV的实验和数值模拟。HUANG等[4]研究了H2-CH4-空气混合物的LBV,发现添加H2会提高LBV,LBV与H和OH的最大自由基浓度之间存在强相关性。XU等[5]测定了正癸烷-氢气-空气混合物的LBV,发现LBV与氢添加比（RH）呈线性关系。LHUILLIER等[6]研究了H2-NH3-空气混合物的LBV,发现燃料中H2分数的增大（体积分数为0% ~ 60%）会增加LBV。
即使没有外部干扰,预混层流火焰也会受到自身不稳定性的影响。这些不稳定的火焰会迅速导致压力增加和燃烧温度升高,从而导致爆震和有害的燃烧排放（如NOx）[7]。此外,火焰不稳定动力学知识有助于燃烧和爆炸安全专家们设计安全措施来减少气体爆炸。XU等[8]开展了二乙基呋喃火焰不稳定性的研究,结果表明,流体动力学效应使火焰不稳定,而热扩散项使火焰稳定。LI等[9]对NH3-H2-空气混合物的细胞不稳定性展开研究,发现增加氢气比例或初始压力可以促进由流体动力失稳模式引起的整体火焰不稳定性。WU等[10]研究了氢气-甲醇球形火焰胞状不稳定性,发现贫氢气-甲醇火焰中的细胞化主要由热扩散的不稳定性控制,而富氢气-甲醇火焰中的细胞化主要由流体动力学不稳定性控制。
截至目前,有关氢气-乙醇-空气预混火焰不稳定性的相关研究尚未有详尽报道。为了更好地理解富氢气-乙醇-空气在高压下的LBV和火焰不稳定性,还需要进行更多的基础实验,以便提供更多有关这方面的数据,形成可靠的研究体系。基于以上分析,本研究的核心目标是考察不同初始条件下氢气-乙醇球形膨胀火焰的层流燃烧特性。在不同的实验条件下,首先对LBV进行了实验研究,其次考察火焰发展不同阶段的火焰形貌,最后讨论固有火焰不稳定性对火焰产生的影响。
1 实验装置和数据处理
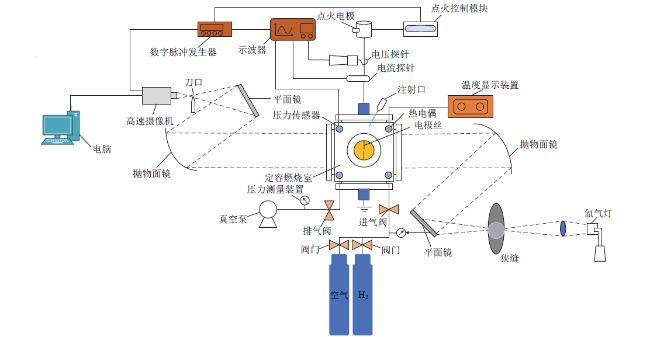
1.1 实验装置
图1为氢气-乙醇燃烧实验装置。该装置由以下几个模块组成：定容燃烧弹、纹影摄影系统、点火系统、数据采集系统以及气体排放与供应系统。定容燃烧弹内通过比例-积分-微分（proportional integral derivative, PID）控制器来控制弹体内壁上加热电极进行加热,采用K型热电偶和压力表分别测定可燃混合物的温度和压强。在实验中,每个工况下至少进行三次实验,以确保实验的重复性和准确性。氢气-乙醇燃料中的乙醇比例${{x}_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH}}}$定义为：
${{x}_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH}}}=\frac{{{V}_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH}}}}{{{V}_{{{\text{H}}_{\text{2}}}}}+{{V}_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH}}}}\times 100\%$ (1)
式中：${{V}_{{{\text{H}}_{\text{2}}}}}$、${{V}_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH}}}$分别为燃料中的H2、C2H5OH的体积分数。
Fig. 1 Diagram of the hydrogen-ethanol combustion experimental setup图1 氢气-乙醇燃烧实验装置图 |
1.2 参数计算
利用边缘检测函数原理结合本实验开发提取火焰半径的程序,在Halcon软件上对所拍摄的纹影图像进行火焰半径提取,根据式（2）计算得到火焰半径：
${{R}_{\text{u}}}=\sqrt{\frac{{{A}_{\text{sch}}}}{A}}R$ (2)
式中：${{R}_{\text{u}}}$为火焰半径;${{A}_{\text{sch}}}$为纹影火焰面积;A为纹影视窗面积;R为视窗实际半径。拉伸火焰速度${{S}_{\text{n}}}$是火焰半径${{R}_{\text{u}}}$对时间t的求导,计算公式如下：
${{S}_{\text{n}}}=\frac{\text{d}{{R}_{\text{u}}}}{\text{d}t}$ (3)
球形火焰在传播过程中受拉伸率$\alpha $的影响,拉伸率定义为在火焰面上无限微小单元面积A对时间t的变化率,其计算公式如下：
$\alpha =\frac{1}{A}\times \frac{\text{d}A}{\text{d}t}=\frac{2}{{{R}_{\text{u}}}}\times \frac{\text{d}{{R}_{\text{u}}}}{\text{d}t}=\frac{2}{{{R}_{\text{u}}}}\times {{S}_{\text{n}}}$ (4)
${{S}_{\text{b}}}-{{S}_{\text{n}}}={{L}_{\text{b}}}\alpha $ (5)
式中：${{L}_{\text{b}}}$为马克斯坦长度。
层流燃烧速度（符号为${{u}_{\text{L}}}$）可通过以下等式计算[11]。
${{u}_{\text{L}}}={{S}_{\text{b}}}\frac{{{\rho }_{\text{b}}}}{{{\rho }_{\text{u}}}}$ (6)
式中：${{\rho }_{\text{b}}}$、${{\rho }_{\text{u}}}$分别为已燃混合气与未燃混合气的密度。
$\sigma =\frac{{{\rho }_{\text{u}}}}{{{\rho }_{\text{b}}}}$ (7)
火焰厚度$\delta $可以由公式（8）[14]通过梯度法得到：
$\delta =\frac{{{T}_{\text{ad}}}-{{T}_{\text{u}}}}{{{\left( \text{d}T/\text{d}x \right)}_{\text{max}}}}$ (8)
$Le=\frac{\gamma }{{{D}_{ij}}}=\frac{\lambda }{{{\rho }_{u}}{{c}_{p}}{{D}_{ij}}}$ (9)
式中：$\gamma $为热扩散率;$\lambda $为导热系数;${{c}_{p}}$为定压比热容;${{D}_{ij}}$为极限反应物的质量扩散率。
此外,混合物中不足和过剩的反应物刘易斯数结合起来产生一个有效刘易斯数[16],如公式（10）所示。
$L{{e}_{\text{eff}}}=1+\frac{\left( L{{e}_{\text{E}}}-1 \right)+\left( L{{e}_{\text{D}}}-1 \right)A}{1+A}$ (10)
式中：$L{{e}_{\text{E}}}$、$L{{e}_{\text{D}}}$分别为混合物中过剩反应物和不足反应物的刘易斯数。$A=1+\beta (\varphi -1)$表示混合强度,对于富混合物,$\varphi =\text{ }\!\!\Phi\!\!\text{ }$,而对于贫混合物,$\varphi ={1}/{\text{ }\!\!\Phi\!\!\text{ }}\;$;其中,Ф为当量比。$\beta $为泽尔多维奇数[14],关系式为$\beta ={{E}_{\text{a}}}/R\left[ \left( {{T}_{\text{ad}}}-{{T}_{i}} \right)/{{T}_{\text{ad}}}^{2} \right]$,其中${{E}_{\text{a}}}$为总活化能,$R$为通用气体常数[16]。${{E}_{\text{a}}}/R=-2\frac{\partial \left[ \text{ln}\left( {{\rho }_{\text{u}}}{{u}_{\text{L}}} \right) \right]}{\partial \left( 1/{{T}_{\text{ad}}} \right)}$定义为活化温度,由未燃气体密度${{\rho }_{\text{u}}}$、层流燃烧速度${{u}_{\text{L}}}$以及绝热火焰温度${{T}_{\text{ad}}}$确定[15]。
LAPALME等[16]提出了一种基于燃料中二元成分的有效刘易斯数表达式,表示如下：
$\frac{1}{L{{e}_{\text{eff}}}}=\frac{\mathop{\sum }_{i=1}^{f}{{x}_{i}}{{D}_{ij}}}{\alpha }=\sum \frac{{{x}_{i}}}{L{{e}_{i}}}$ (11)
式中：${{x}_{i}}$为各单燃料i在多燃料混合物中的体积分数;$L{{e}_{i}}$为各单燃料i的有效刘易斯数。
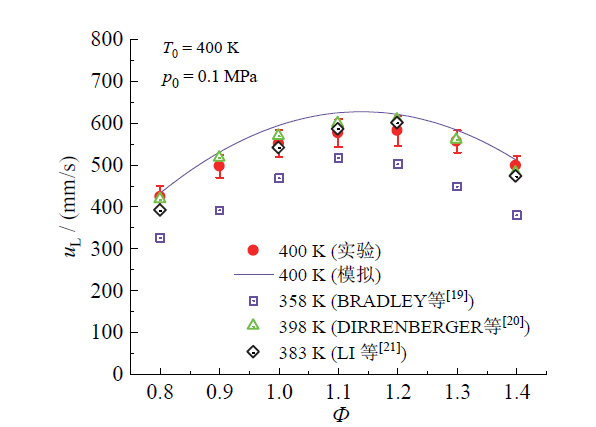
1.3 系统验证和误差分析
在实验中,由于压力表的精度误差$u({{p}_{0}})$、热电偶测量的精度误差$u({{T}_{0}})$以及微型注射器的精度误差$u(V)$,从而导致存在一个等效的比率误差$u(\varphi )$。$u({{p}_{0}})$、$u(V)$和$u(\varphi )$可由式（12） ~ 式（15）计算。
$u({{p}_{0}})={{x}_{p}}\times {{p}_{x}}$ (12)
式中：${{x}_{p}}$为压力传感器的精度（0.05%）;${{p}_{x}}$为压力传感器的范围。
$u({{T}_{0}})=0.005{{T}_{0}}-273/\sqrt{3}$ (13)
式中：${{T}_{0}}$为初始温度,本实验中使用的K型热电偶的精度为 ±0.5%。
$u(V)=a/k$ (14)
式中：a为仪器精度的一半,通常基于均匀分布的假设,取$k=\sqrt{3}$。由于实验所用的乙醇在室温下是液态,在不同的条件下,注射量范围较大,因此选用的注射器也有不同的范围,包括50 μL、100 μL和200 μL,其精度分别为0.5 μL、1 μL和2 μL。综上所述导致的最终误差由以下公式计算：
$u(\varphi )=\sqrt{\frac{\partial {{\varphi }^{2}}}{\partial {{p}_{0}}}{{u}^{2}}{{p}_{0}}+\frac{\partial {{\varphi }^{2}}}{\partial {{T}_{0}}}{{u}^{2}}{{T}_{0}}+\frac{\partial {{\varphi }^{2}}}{\partial V}{{u}^{2}}V}$ (15)
对于本研究中的LBV而言,最终计算出的$u(\varphi )$小于3.4%,在允许的误差范围内。
2 结果与讨论
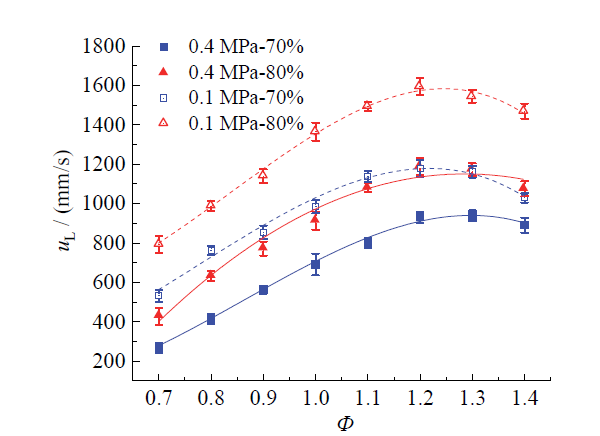
2.1 层流燃烧速度
图3是不同初始条件下氢气-乙醇-空气预混合火焰LBV的变化规律。从图中可以看出,LBV随着当量比Ф增加呈现先增大后减小的趋势,在Ф = 1.2时LBV最大。这是由于在贫燃阶段,燃料与氧气充分反应,释放出大量的热,提高了火焰传播的速度。由于实验存在热损失,因此LBV的峰值出现在理论值（Ф = 1.0）之后。而在富燃阶段,由于氧气不足,燃料无法充分反应,释放热量减少,LBV减小。在所有实验的Ф下,初始压力对氢气-乙醇火焰的LBV有负面影响。在初始压力相同的环境中,燃料中氢气比例的提高会使LBV增大。这主要是由于氢气比例的上升使得H摩尔分数快速上升,也促进了乙醇氧化反应使得O和OH摩尔分数发生了较大的变化,加快了氢气-乙醇-空气预混合火焰的LBV。
Fig. 3 Laminar combustion velocity variation curves图3 LBV变化曲线 |
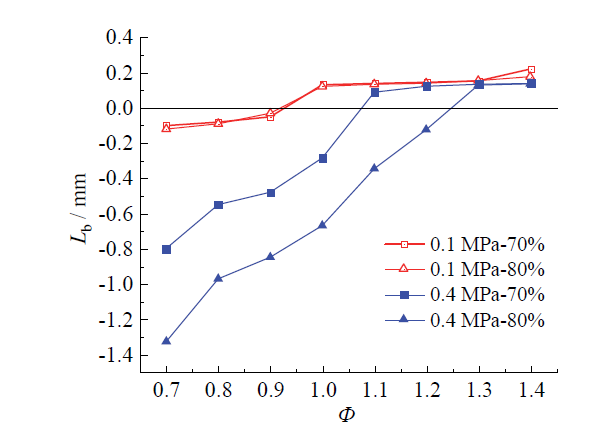
2.2 马克斯坦长度
燃烧混合物的马克斯坦长度（Lb）是表征燃烧速度对火焰拉伸的敏感性的重要参数[7]。根据公式（5）,正Lb表示LBV随$\alpha $的增大而减小,火焰倾向在稳定状态下传播。而负Lb意味着LBV随着$\alpha $的增大而增加,并且火焰不稳定发生[13]。图4显示了初始温度为400 K、初始压力为0.1 MPa和0.4 MPa、氢气比例为70%和80%的条件下,氢气-乙醇混合物的Lb。由图可知,Lb随氢气浓度的增加而减小,火焰不稳定性增强,贫混合比富混合的减少更明显。在固定压力下,Lb随Ф的减小单调减小,说明较浓氢气-乙醇的火焰传播比较稀混合物更稳定。在0.4 MPa时,虽然在富混合物时火焰前沿扰动加剧,出现褶皱,但火焰拉伸的影响仍然显著,因此Lb > 0,火焰仍然稳定。此外,随着压力的增加,Lb显著降低,并且Lb下降到负值所对应的位置点也移动到更稀的混合物侧。这意味着较高的压力可使氢气-乙醇火焰遭受更不稳定的传播。
Fig. 4 Variation of Markstein length with equivalence ratio图4 马克斯坦长度随当量比的变化曲线 |
2.3 火焰形貌
采用高速纹影成像系统来捕捉球形膨胀火焰的传播以及火焰表面蜂窝结构的形成和发展。图5记录了氢气比例为80%和压力为0.4 MPa条件下的氢气-乙醇预混火焰的纹影图像。从图中可以看出,在初期阶段,球形火焰前锋面由于高强度的拉伸和曲率的影响较为光滑,火焰处于稳定状态[9,14]。随着火焰半径增大,球形火焰前锋面拉伸和曲率的影响减小,导致火焰不稳定,主要表现为火焰前锋面开始出现大裂纹并不断分裂成小裂纹,最终形成尺度不均的胞化状态[14]。在相同的火焰半径下,贫氢气-乙醇预混球形火焰失稳严重（Ф = 0.7）,火焰轮廓高度褶皱,可以看到尖瓣凸起。而随着Ф的增大,火焰失稳的能力变弱,在其表面形成细胞的数量减少。上述分析与图4中的Lb表现一致。
Fig. 5 Schlieren images of hydrogen-ethanol premixed flame at 80% hydrogen ratio and 0.4 MPa pressure图5 氢气比例为80%和0.4 MPa压力下氢气-乙醇预混火焰的纹影图像 |
图6为氢气比例为80%及不同初始压力下氢气-乙醇的火焰纹影图像。从图中可以看出,当初始压力为0.1 MPa时,火焰表面保持光滑,没有火焰不稳定现象产生。当初始压力为0.4 MPa时,贫氢气-乙醇火焰前锋面出现蜂窝状结构,富氢气-乙醇和化学当量比火焰表面出现大量裂纹和胞状结构。因此初始压力的增大对火焰形貌有着显著影响,主要表现为火焰表面出现凹槽,胞状结构显著增加,火焰不稳定性增强。
Fig. 6 Flame schlieren images of hydrogen-ethanol at different initial pressures图6 不同初始压力下氢气-乙醇的火焰纹影图像 |
2.4 固有火焰不稳定性
LAW[22]总结了三种类型的火焰不稳定性,即流体力学不稳定性、热扩散不稳定性和浮力不稳定性。现有的研究表明,在火焰燃烧过程中,只要火焰的传播速率不是太低,浮力不稳定性几乎不会影响火焰,可以近似忽略[9]。因此,在球形火焰的传播过程中,流体力学不稳定性和热扩散不稳定性是研究的重点。流体动力学不稳定性本质上是火焰前锋面的密度跳动,引起火焰前锋面在位置上发生相对移动[12]。此外,火焰前锋面厚度较薄会导致流体动力学不稳定性增强。因此当热膨胀比增大或者火焰厚度减小,流体动力学不稳定性增强。图7展示了不同初始压力和氢气比例下的热膨胀比和火焰厚度随Ф的变化。从图中可以很清楚地看到,热膨胀比均随着Ф先增大后减小,在Ф = 1.1时达到最大值,而火焰厚度的变化趋势正好相反,在Ф = 1.2时达到最小值。图7a中热膨胀比随着氢气比例升高而减小,压力变化对热膨胀比略有影响,初始压力增大,热膨胀比略有上升[7,15-16]。此外,图7b中火焰厚度随着氢气比例和初始压力的增大均显著减小,一方面火焰曲率对火焰的稳定作用变弱,火焰前锋面更易发生形变,火焰趋于不稳定,流体动力学不稳定性显著增强;另一方面火焰厚度控制着褶皱火焰面上产生的斜压扭矩对火焰稳定性的影响,火焰厚度减小和热膨胀比增大都会导致斜压扭矩增大,进而增强流体动力学不稳定。
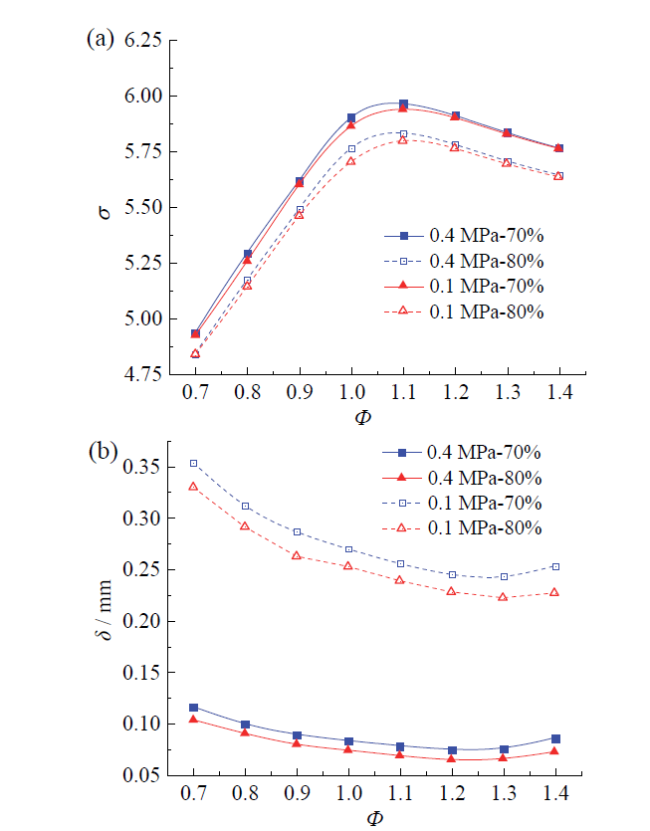
Fig. 7 Variation of thermal expansion ratio and flame thickness with equivalent ratio: (a) thermal expansion ratio; (b) flame thickness图7 热膨胀比和火焰厚度随当量比的变化：（a）热膨胀比;（b）火焰厚度 |
图8描述了Leeff随Ф的变化情况。从图中可以看出,Leeff对初始压力变化并不敏感,由于贫氢气-乙醇中质量扩散的增加,Leeff均随着Ф的增大而增大,火焰热扩散不稳定性减弱[3,14]。而随着氢气比例升高,Leeff呈现降低的趋势,表明较高氢气比例下,火焰热扩散不稳定增强。在氢气含量为70%时,Leeff始终大于1,因此可以充分抑制热扩散不稳定性,这意味着火焰前锋面出现的不稳定性仅由流体动力学效应表现出来的。氢气含量为80%时,与化学计量比和富氢气-乙醇相比,贫氢气-乙醇的Leeff小于1,表明贫氢气-乙醇具有更强的热扩散不稳定性,这时热扩散效应是不稳定的,从图5中可以发现贫氢气-乙醇传播初期火焰轮廓高度褶皱,可以看到尖瓣凸起,随着传播时间的增加,减弱了火焰尺寸的细胞性和褶皱的程度,而由于火焰前锋面的密度跳动和火焰厚度的必然存在,流体动力学不稳定则一直作用于火焰传播阶段,因此火焰前锋面胞状结构的形成是流体动力不稳定性和热扩散不稳定性共同作用的结果。
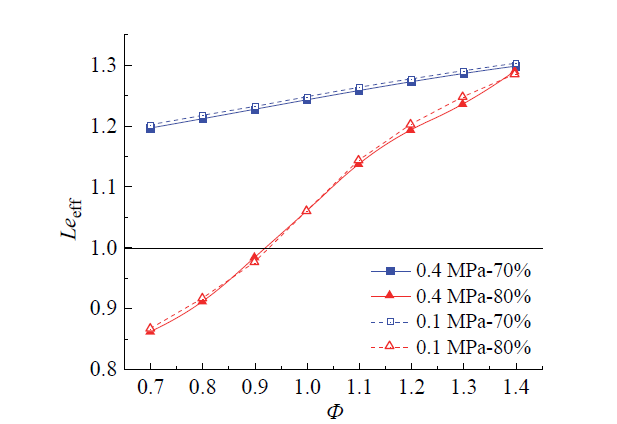
Fig. 8 Variation of effective Lewis number with equivalence ratio图8 有效刘易斯数随当量比的变化情况 |
3 结论
在初始温度为400 K、不同初始压力（0.1 MPa、0.4 MPa）、氢气比例（70%、80%）和当量比（0.7 ~ 1.4）条件下进行了氢气-乙醇预混燃烧实验。主要结论如下：
（1）所有实验当量比下,测得层流燃烧速度随着压力的增加而明显降低,在固定压力下,峰值出现在当量比为 1.2处。在初始压力相同的环境中,燃料中氢气比例的提高会加快层流燃烧速度,且Xh = 80%比Xh = 70%的层流燃烧速度提升幅度更为明显。
（2）随着初始压力的增加,所有当量比对应的热膨胀比和有效刘易斯数仅略微变化,但是火焰厚度显著减小,导致流体动力不稳定性增强。此外,氢气比例升高,热膨胀比随之减小,流体动力学不稳定性减弱。有效刘易斯数对氢气比例的变化敏感,随着氢气比例的增加,在贫氢气-乙醇火焰中具有很强的热扩散不稳定性。这表明火焰在贫燃料侧和较高初始压力下以更不稳定的状态传播。此外,通过观察不同初始条件下马克斯坦长度随当量比的变化趋势,这一点也得到了确切的验证。
（3）在Xh = 70%时,火焰前锋面出现的不稳定性仅由流体动力学效应引起。而对于Xh = 80%时,贫氢气-乙醇火焰前锋面胞状结构的形成则是流体动力不稳定性和热扩散不稳定性共同作用的结果。
