0 引言
研究者们对扭曲椭圆管内流体流动特性和传热性能开展了实验和数值模拟研究。YANG等[7]在雷诺数Re为600 ~ 55 000范围内,以水为工质实验研究了扭曲椭圆管内层流、过渡流和湍流时的传热和流动特性,得到了传热系数和流动阻力的准则关联式。还有学者对扭曲椭圆管外流动传热特性进行了研究。思勤等[8]对扭曲椭圆管换热器壳侧和管侧工作介质分别为水和油的传热性能进行了实验研究,得到了壳侧和管侧努塞尔数和摩擦系数的实验关联式。LIU等[9]和DONG等[10]通过对实验数据的拟合分别得到了在纵向流情况下扭曲椭圆管束对流传热性能和流动阻力特性计算的准则关联式。这些扭曲椭圆管内外的准则关联式对设计换热器具有理论指导意义。
还有一些学者利用场协同原理和扭曲椭圆管内二次流的演变规律,对强化传热性能进行分析以探索对流传热强化机理。马芳芳等[11]利用计算流体力学（computational fluid dynamics, CFD）技术对扭曲椭圆管内介质为水的传热和流动阻力特性进行了数值模拟,得到不同工况下的温度场、压力场及速度场,并基于场协同原理对其温度与速度梯度的协同效果及压力与速度梯度的协同效果进行比较和分析,获得不同工况下传热与流动阻力特性随长短轴比变化的规律,分析了影响扭曲椭圆管内流体传热效果与流动阻力损失的因素及其传热强化的机理。CHANG等[12]发现扭曲椭圆管内二次流强度以及传热和流阻特性均与长短轴比和扭曲比紧密相关,长短轴比越大或扭曲比越小,二次流强度越强且流动阻力也越大,进而传热强化效果就越显著。近些年,众多学者将热力学定律和火积理论用于评价扭曲椭圆管内对流传热性能。CHEN等[13]比较了采用熵产理论和火积耗散理论对传热强化的优化效果,研究表明,在相同的限制条件下,熵产最小的优化导致最佳的热功转换效率,而火积耗散极值原理的优化导致最佳的对流传热效率。EBRAHIMI等[14]采用热力学第二定律探究了微型扭曲椭圆管内强化传热机理,结果表明,较低的能量不可逆损失导致扭曲椭圆管内传热增强。
综上所述,目前针对对流传热优化设计的研究主要是基于热力学第一定律,即从能量的数量上进行传热强化评价,而对流传热中包含温差的热量传递和流体流动摩擦阻力损失,这些过程均为不可逆过程,往往会引起能量在质上的贬值。传热及流动中的不可逆损失所引起熵产已得到重视,并被用于评估热力系统热力学性能和热力设备的结构优化[15,16,17]。如ZHENG等[18]通过熵产分析对肋槽换热管的热工水力性能进行了数值研究,结果表明,肋槽换热管的最佳设计参数组合可以使熵产最小且综合传热性能最优。尽管熵产最小化原理已普遍应用于多种强化换热管的优化设计,但将熵产理论用于分析扭曲椭圆管内对流传热特性的研究还较为少见。为此,本文从热力学第二定律的角度,利用熵产最小化原理,分析不同结构参数的扭曲椭圆管内总熵产的变化规律,以期揭示扭曲椭圆管的传热强化机理。
1 数值计算方法
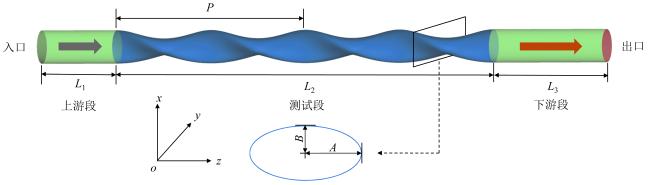
1.1 物理模型
扭曲椭圆强化传热管结构如图1所示,采用Solidworks软件对其建立模型,其由内径（d）为20 mm的铝质光滑圆管加工而成,对于具有不同长短轴比的扭曲椭圆管所对应的当量直径（D）取值分别为19 mm和17 mm。由中心复合设计法得出扭曲比和长短轴比的设计参数,具体参数见表1。测试段（L2）作为计算区域,长度为1 000 mm,为了保证在测试段入口处为充分发展的湍流并且消除出口回流对测试段的影响,设计了上游段（L1）和下游段（L3）,长度分别为100 mm和160 mm。长短轴比（A/B）定义为椭圆横截面长轴和短轴的比值;扭曲节距（P）定义为椭圆形横截面扭转360°所对应管轴方向的长度;扭曲比（P/D）定义为扭曲节距和当量直径的比值。
Fig. 1 Schematic diagram of enhanced heat transfer tube structure图1 强化传热管结构示意图 |
Table 1 Values of design parameters表1 设计参数的取值 |
| 设计参数 | 取值 |
|---|---|
| Re | 710、1 500、2 750、4 000、4 790 |
| A/B | 1.34、1.50、1.75、2.00、2.16 |
| D/mm | 19、19、17、17、17 |
| P/D | 26.33、23.53、19.12、14.70、11.90 |
1.2 控制方程
在三维稳态数值模拟中,采用Renormalization group（RNG）k-ε湍流模型对流体进行计算,控制方程为质量、动量和能量方程[19],计算式如下。
质量方程：
$\frac{\partial \left( \rho {{u}_{i}} \right)}{\partial {{x}_{i}}}=0$ (1)
动量方程：
$\frac{\partial \left( \rho {{u}_{i}}{{u}_{j}} \right)}{\partial {{x}_{i}}}=-\frac{\partial p}{\partial {{x}_{i}}}+\mu \frac{\partial }{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)$ (2)
能量方程：
$\begin{align} & \frac{\partial }{\partial {{x}_{i}}}\left( \rho {{T}_{\text{m}}} \right)+\frac{\partial }{\partial {{x}_{i}}}\left( \rho {{u}_{i}}{{T}_{\text{m}}} \right)=-p\frac{\partial {{u}_{i}}}{\partial {{x}_{i}}}+ \\ & \lambda \frac{\partial }{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right) \end{align}$ (3)
湍流动能k方程和湍流动能耗散率ε方程[20]的计算式如下。
湍流动能k方程：
$\begin{align} & \frac{\partial \left( \rho {{u}_{i}}k \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +\frac{{{v}_{\text{m}}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+ \\ & {{\eta }_{t}}\frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-\rho \varepsilon \end{align}$ (4)
湍流动能耗散率ε方程：
$\begin{align} & \rho \frac{\partial \left( {{u}_{j}}\varepsilon \right)}{\partial {{x}_{j}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +\frac{{{v}_{\text{m}}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+{{c}_{1}}\rho S\varepsilon - \\ & {{c}_{2}}\rho \frac{{{\varepsilon }^{2}}}{k+\sqrt{v\varepsilon }} \end{align}$ (5)
式中：${{c}_{1}}=\max \left[ 0.43,\frac{\eta }{\eta +5} \right]$;$\text{ }\eta \text{=}\frac{Sk}{\varepsilon }$;$\text{ }S=\sqrt{2{{S}_{i,j}}\text{ }{{S}_{i,j}}}$;${{S}_{i,j}}=\frac{1}{2}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)$;c2 = 1.9;σε = 1.2;σk = 1.0;μ= cμρk2/ε。
1.3 边界条件及计算方法
数值模拟计算时边界条件设定如下：入口处给定均匀速度,流体温度设置为303.15 K,出口处为压力出口;测试段管壁面为无滑移壁面且壁温恒定为343.15 K,上游段和下游段壁面均为绝热壁面;工作介质设置为不可压缩流——水（热物理性质见表2）,不考虑重力和黏性耗散的影响;选择SIMPLE算法将动量方程和连续性方程分别离散以得到满足连续性条件的速度场和压力场;动量、能量、湍流动能及湍流动能耗散率的求解采用二阶迎风格式;收敛的残差标准设置为1.0 × 10-6。
Table 2 Thermophysical properties of working fluid表2 工质热物理性质 |
| 参数 | 取值 |
|---|---|
| 比热容cp/[J/(kg∙K)] | 4 174 |
| 动力黏度μ/(Pa∙s) | 5.49 × 10-4 |
| 密度ρ/(kg/m3) | 988.1 |
| 普朗特数Pr | 3.54 |
| 热导率λ/[W/(m∙K)] | 0.648 |
1.4 参数定义
平均对流传热系数、当量直径、雷诺数、努塞尔数、流动摩擦系数和压降公式列于表3。
Table 3 Parameter definition formula for twisted elliptical tubes表3 扭曲椭圆管参数定义公式 |
| 变量名称 | 公式 | 序号 |
|---|---|---|
| 对流传热系数 | $h={q}/{\left( {{T}_{\text{w}}}-{{T}_{\text{m}}} \right)}\;$ | (6) |
| 当量直径 | $D={4{A}'}/{U}\;$ | (7) |
| 雷诺数 | $Re={\rho {{v}_{\text{m}}}D}/{\text{ }\!\!\mu\!\!\text{ }}\;$ | (8) |
| 努塞尔数 | $Nu={hD}/{\lambda }\;$ | (9) |
| 摩擦系数 | $f={2D\Delta p}/{\left( {{L}_{2}}\rho v_{\text{m}}^{2} \right)}\;$ | (10) |
| 压降 | $\Delta p={{p}_{\text{in}}}-{{p}_{\text{out}}}$ | (11) |
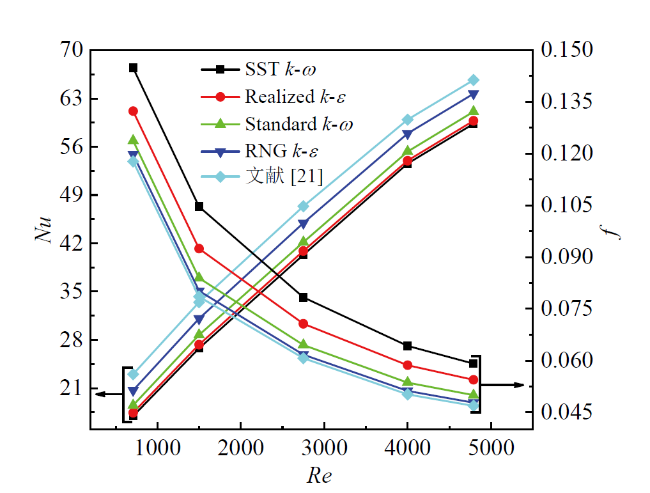
1.5 湍流模型验证
采用Fluent软件对三维计算区域进行数值模拟。为确保上述所建立模型及其数值计算方法的准确性与可靠性,选择合适的湍流模型对扭曲椭圆管内传热和流动特性进行模拟分析。在本文确定的工况下,基于RNG k-ε、Realized k-ε、Standard k-ω及Shear stress transport（SST）k-ω四种湍流模型进行数值计算,将数值模拟结果与实验结果[21]对比,如图2所示。由图可知,当采用RNG k-ε湍流模型时,Nu与f的数值计算结果与实验结果最为接近,且与实验结果的平均偏差分别为8.5%和2.4%,在工程所允许的误差范围内,这说明采用RNG k-ε湍流模型对所建立模型进行数值模拟是准确且可靠的。
Fig. 2 Comparison of numerical simulation and experimental results图2 数值模拟和实验结果对比 |
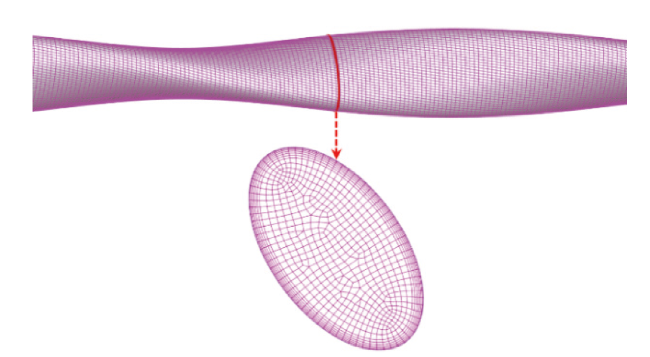
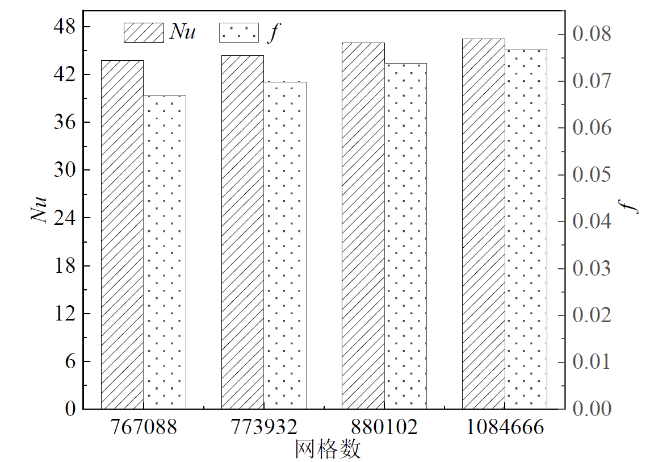
1.6 网格生成和独立性验证
使用计算流体力学前处理软件ICEM CFD对扭曲椭圆管模型进行网格划分。考虑模型结构的不规则性以及管内流动的湍动特性,对扭曲椭圆管进行网格划分时,管内近壁面处设置第一层网格高度的y+ 值接近1,具体的加密网格划分如图3所示。为避免网格数量对数值计算结果的影响及确定其结果的准确性,有必要对模型结构进行网格无关性验证,此处以管型（P/D = 19.12、A/B = 1.75）为例进行网格无关性分析。在Re为2 750时,选取四套不同尺寸的网格系统（粗、中细、细和更细）进行计算模拟,网格数分别为767 088、773 932、880 102、1 084 666。Nu和f随网格数的变化如图4所示。由图可得,细（880 102）和更细（1 084 666）的网格系统计算出的Nu和f相对偏差为1.1%和4.1%。在保证节约计算时间及计算结果准确条件下,综合考虑计算效率和求解精度,选用网格数为880 102的网格划分方法进行数值模拟计算。
Fig. 3 Grid division图3 网格划分 |
Fig. 4 Variation of Nu and f with the number of grids图4 Nu和f随网格数的变化 |
2 结果与讨论
2.1 流场和温度场分布
在分析设计参数对管内传热和流动特性的影响之前,首先要探究管内流动曲线、速度分布和温度分布。利用Tecplot软件对扭曲椭圆管内流场和温度场进行可视化后处理,以反映流动和传热特性。
当Re为4 000时,不同节距的扭曲椭圆管（A/B = 2.00）内局部流动曲线和速度分布如图5所示,在管中心位置流体沿管轴线方向流动且速度随P的减小而增大。由于存在壁面剪切应力,管内中心处的速度大于近壁面处的速度,流线由管中心直线形状逐渐向管壁面变化为螺旋扭曲形状,随P减小,管壁附近流体流动曲线螺旋化程度更显著。流体在扭曲流道引导下,受管壁面扰动的影响,在管壁附近形成螺旋流,且在离心力的作用下,流动方向发生周期性改变。此外,可以看出螺旋流随P的减小更加剧烈,主要是由于P越小,在一定长度的扭曲椭圆管上的节距数量越多,流体湍动程度增强,对壁面附近的边界层扰动作用增强,强化了传热效果。
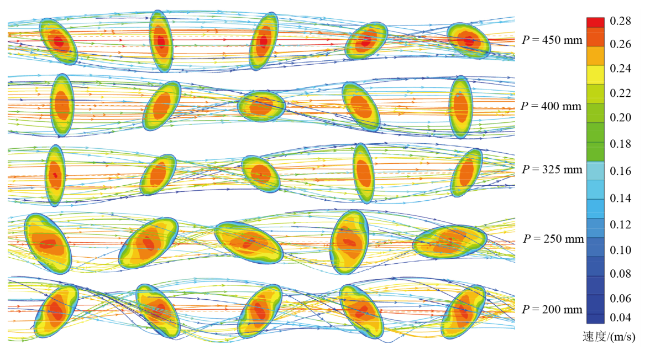
Fig. 5 Local flow curve and velocity distribution in twisted elliptical tube图5 扭曲椭圆管内局部流动曲线和速度分布 |
当Re为4 790时,扭曲椭圆管（A/B = 2.16,P/D = 11.90）轴向不同横截面的温度分布如图6所示。由图可知近壁面区域的温度较高,且随流体从入口端沿轴线朝向出口端流动时,管中心区域的流体温度显著升高,说明扭曲椭圆管内较大径向速度形成的螺旋流改变了管内流场结构,使温度场分布发生了变化,促进了中心区域和近壁面区域之间流体的混合,流体从近壁面向中心区域传递更多的热量以实现管内强化传热。在中下游横截面上的温度分布更均匀,主要归因于近壁面的温度梯度更大,增大了流体湍流强度进而增强了流体的扰动。此外,由于在长轴端形成的涡流方向相反,横截面上的温度分布形状大致呈现“S”形。
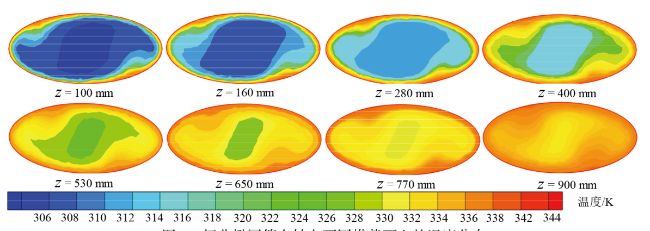
Fig. 6 Temperature distribution of twisted elliptical tube on different axial cross sections图6 扭曲椭圆管在轴向不同横截面上的温度分布 |
2.2 结构参数对传热和流动特性的影响
在传热计算中,h和ΔP通常表示传热性能和流动阻力损失。为揭示扭曲椭圆管的长短轴比对传热性能和流动特性的影响,当P/D = 19.12时,考察不同长短轴比的扭曲椭圆管内h和ΔP随Re的变化,如图7所示。不同长短轴比的扭曲椭圆管内h和ΔP都随Re的增大而增大,说明传热性能增强必然使压降损失增大。对于给定的Re,h和ΔP均随长短轴比的增大而增加,表明较大A和较小B能够使切向和径向速度快速交替变化并生成更多的小尺度涡流,促进核心区域和近壁面区域之间流体的混合以提高传热效率。但由于速度在切向和径向方向快速变化,流体沿着流动方向形成较大的压力梯度,且在近壁面区域集中混合,导致更大的流动阻力损失。
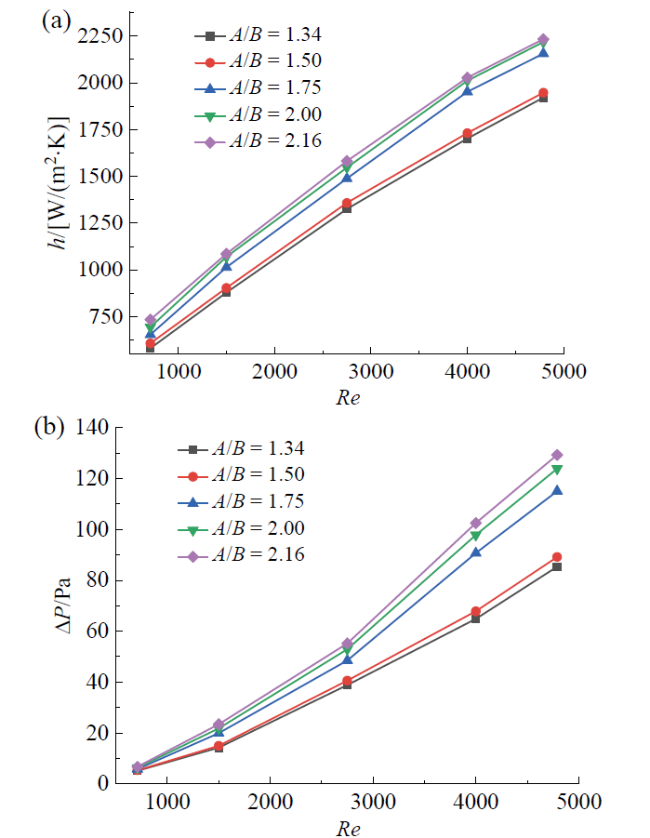
Fig. 7 Variation of h and ΔP with Re in twisted elliptical tubes with different A/B when P/D = 19.12图7 P/D = 19.12时,不同A/B的扭曲椭圆管内h和ΔP随Re变化 |
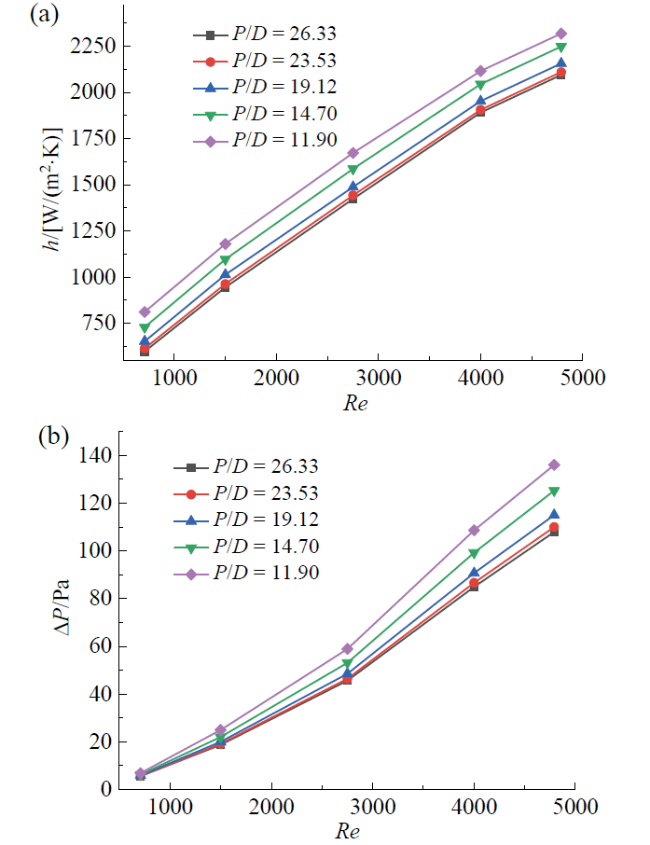
Fig. 8 Variation of h and ΔP with Re in twisted elliptical tubes with different P/D when A/B = 1.75图8 A/B = 1.75时,不同P/D的扭曲椭圆管内h和ΔP随Re的变化 |
2.3 熵产分析
任何被动强化传热技术均会增大流动功耗,不可避免地增加熵产。为提高强化传热效率,并获得传热过程中引起的不可逆与换热管传热性能之间的关系,利用BEJAN[15]提出的熵产最小化方法分析扭曲椭圆管内由传热和流动过程引起的不可逆损失以估算复杂传热和流动过程的能量耗散,该方法是一种从热力学第二定律角度对特定热力学系统优化的方法。在熵产最小化的情况下对流动通道或热力学系统进行优化设计,由于流体在水平扭曲椭圆管内流动,重力对流动的影响较小,且速度大小几乎不变,势能和动能变化忽略不计。沿着流动方向长度为dz的扭曲椭圆管微元体为热力学系统,热力学第一定律和第二定律表示如下。
$\dot{m}\text{d}h\text{=}{q}'\text{d}z$ (12)
$\text{d}{{{S}'}_{\text{gen}}}=\dot{m}\text{d}s-{{q}'\text{d}z}/{\left( T+\Delta T \right)}\;$ (13)
由热力学关系式得：
${\text{d}h}/{\text{d}z}\;=T\left( {\text{d}s}/{\text{d}z}\; \right)+\left( {1}/{\rho }\; \right)\left( {\text{d}P}/{\text{d}z}\; \right)$ (14)
$\Delta {{{S}'}_{\text{gen}}}={\text{d}{{{{S}'}}_{\text{gen}}}}/{\text{d}z}\;$ (15)
$\Delta {{{S}'}_{\text{gen}}}={{q}'\Delta T}/{{{T}^{2}}\left( 1+\tau \right)}\;-\left( {{\dot{m}}}/{\rho T}\; \right)\left( {\text{d}P}/{\text{d}z}\; \right)$ (16)
压降表示为：
$\text{d}P=-\left( {2f{{G}^{2}}}/{\rho D}\; \right)\text{d}z$ (17)
质量流速：
$G={{\dot{m}}}/{{{A}'}}\;$ (18)
无量纲温差$\tau \text{=}{\left( {{T}_{\text{w}}}-{{T}_{\text{in}}} \right)}/{{{T}_{\text{in}}}}\;$忽略不计,q′和ΔT以St形式表示为：
$St={{{q}'}}/{U\Delta T{{c}_{p}}G}\;$ (19)
代入等式（16）化简得：
$\Delta {{{S}'}_{\text{gen}}}={{{{{q}'}}^{2}}D}/{\left( 4{{T}^{2}}\dot{m}{{c}_{p}}St \right)}\;+{2{{{\dot{m}}}^{3}}f}/{\left( {{\rho }^{2}}TD{{{{A}'}}^{2}} \right)}\;$ (20)
通常,等式（20）是由传热和摩擦效应影响的熵产组合,由式（21）和式（22）表示如下。
${{\left( \Delta {{{{S}'}}_{\text{gen}}} \right)}_{\Delta T}}={{{{{q}'}}^{2}}D}/{\left( 4{{T}^{2}}\dot{m}{{c}_{p}}St \right)}\;$ (21)
${{\left( \Delta {{{{S}'}}_{\text{gen}}} \right)}_{\Delta P}}={2{{{\dot{m}}}^{3}}f}/{\left( {{\rho }^{2}}TD{{{{A}'}}^{2}} \right)}\;$ (22)
(ΔS′gen)ΔT和β(ΔS′gen)ΔP分别表示由传热和流动摩擦力引起的不可逆损失。PAOLETTI等[23]对由传热引起的不可逆损失相对于总熵产的大小提出了不可逆性分布参数Be,一个无量纲参数定义如下：
$Be\text{ =}{\text{ }{{\left( \Delta {{{{S}'}}_{\text{gen}}} \right)}_{\Delta T}}}/{\Delta {{{{S}'}}_{\text{gen}}}}\;$ (23)
图9（a、b）为A/B = 1.75和P/D = 11.90时,扭曲椭圆管内总熵产随Re的变化情况,对于给定的Re,扭曲椭圆管内总熵产随P/D的减小或A/B的增大而增大;对于相同的A/B或P/D,总熵产随Re的增大均增大,说明总熵产变化受结构参数和流动参数共同作用的影响。当P/D = 19.12时,不同A/B的扭曲椭圆管内 (ΔS′gen)ΔT和β(ΔS′gen)ΔP随Re的变化如图10所示,图中可见,(ΔS′gen)ΔT和β(ΔS′gen)ΔP随Re的增加分别减小和增大,且β(ΔS′gen)ΔT均大于 (ΔS′gen)ΔP,说明熵产受传热过程的影响更大,这是由于Re增加使流体传热性能增强,流场中的温度分布更加均匀,整体流动温度降低,从而降低了由传热引起的不可逆损失。与此同时,Re增加会导致更大的流体黏度和速度梯度,增大了扭曲椭圆管内流动摩擦引起的不可逆损失。
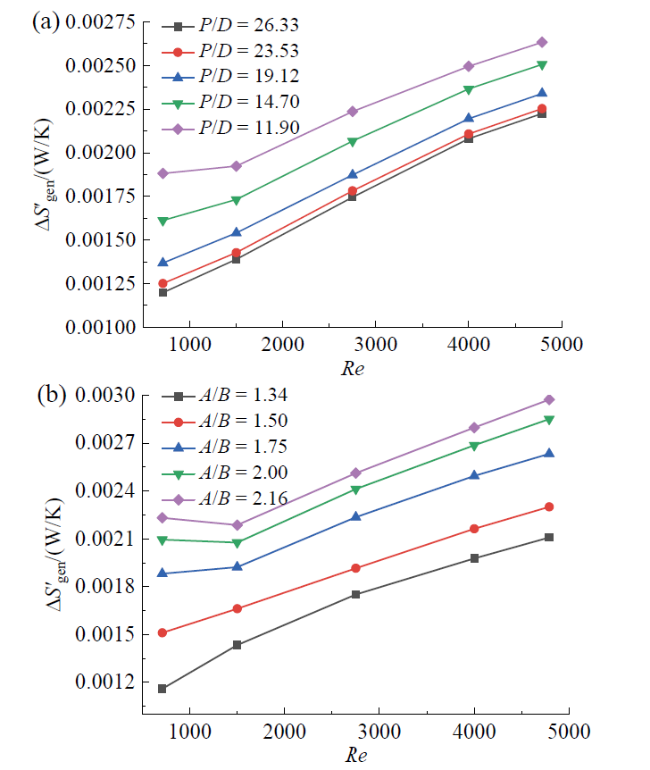
Fig. 9 Variation of ΔS′gen in a twisted elliptical tubes with different Re: (a) P/D (A/B = 1.75); (b) A/B (P/D = 11.90)图9 扭曲椭圆管内ΔS′gen随Re的变化：（a）P/D（A/B = 1.75）;（b）A/B（P/D = 11.90） |
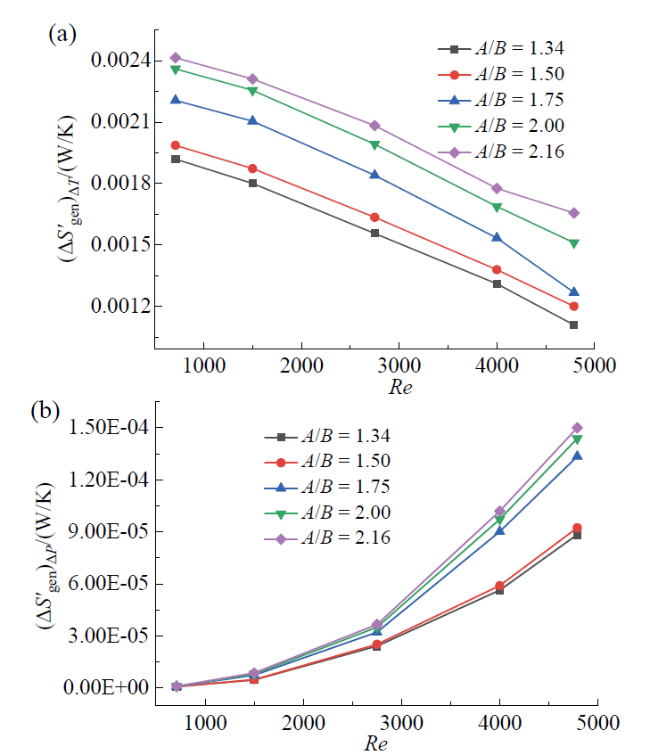
Fig. 10 Variation of (ΔS′gen)ΔT and (ΔS′gen)ΔP with Re in a twisted elliptical tubes with different A/B when P/D = 19.12图10 P/D = 19.12时,不同A/B的扭曲椭圆管内β(ΔS′gen)ΔT和β(ΔS′gen)ΔP随Re的变化 |
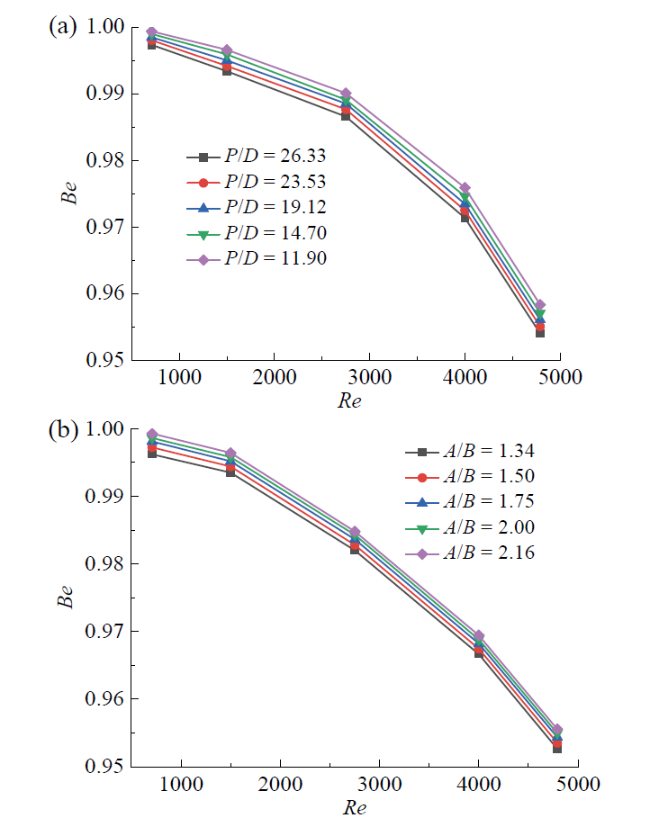
Fig. 11 Variation of Be in a twisted elliptical tubes with different Re: (a) P/D (A/B = 1.50); (b) A/B (P/D = 19.12)图11 扭曲椭圆管内Be随Re的变化：（a）P/D（A/B = 1.50）;（b）A/B（P/D = 19.12） |
综上,根据熵产最小化原理对数值模拟结果进行分析以揭示扭曲椭圆管内传热强化机理。结果表明,扭曲椭圆管内提高传热性能的同时增大了由传热和流动过程引起的不可逆损失。
3 结论
基于实验验证,采用数值计算方法分析结构和流动参数对扭曲椭圆管内对流传热性能及流动阻力特性的影响,进而采用熵产理论揭示扭曲椭圆管内强化对流传热机理,在Re为710 ~ 4 790范围内,具体结论如下：
（1）不同结构参数的扭曲椭圆管内h和ΔP随Re增大均增大;对于给定的Re,h和ΔP随A/B的增大或P/D的减小而增大,而且在A/B = 2.16和P/D = 11.90,h和ΔP均达到最大值。
（2）不同结构参数的扭曲椭圆管内总熵产均随Re的增大而增大;对于一定的Re,总熵产随A/B的增大或P/D的减小而增大;(ΔS′gen)ΔT和(ΔS′gen)ΔP随Re增大分别增大和减小。
（3）当P/D = 26.33和A/B = 1.34时,总熵产达到最小。当P/D = 11.90和A/B = 2.16时,Be均接近1,说明由传热引起的不可逆损失远大于由流动摩擦引起的不可逆损失。
符号表：
A 半长轴,mm
A′ 扭曲椭圆管横截面面积,m2
B 半短轴,mm
Be 不可逆性分布参数
D 当量直径,mm
d 圆管内径,mm
dS′gen 熵产率,W/K
ε 湍流动能耗散率,%
s 比熵产率,W/(kg∙K)
τ 无量纲温差,%
cp 比热容,J/(kg∙K)
ρ 密度,kg/m3
Pr 普朗特数
λ 热导率,W/(m∙K)
μ动力黏度,Pa∙s
f 流动摩擦系数
G 质量流速,kg/(m2∙s)
h 对流传热系数,W/(m2∙K)
k 湍流动能,m2/s2
L 管长,mm
L1 上游段长度,mm
L2 测试段长度,mm
L3 下游段长度,mm
$\dot{m}$ 质量流量,kg/s
Nu 努塞尔数
P 扭曲节距,mm
q 壁面与流体间的平均热流量,W/m2
q′ 换热管单位长度的热流密度,W
Re 雷诺数
St 斯坦顿数
T 温度,K
Tw 壁面温度,K
Tm 流体平均温度,K
U 横截面润湿周长,m
$\nu $ 运动黏度,m2/s
vm 管中流体的平均速度,m/s
Δp 测试段进口和出口的压差,Pa
ΔT 壁面和流体温度差,K
ΔS′gen 总熵,W/K
(ΔS′gen)ΔT 由传热产生的熵,W/K
(ΔS′gen)ΔP 由流体摩擦力产生的熵,W/K
下角标：
in 入口
out 出口
m 平均
w 壁面
