0 引言
天然气水合物是主体水分子借助氢键结合形成笼型晶格,客体分子被包围在晶格之中而形成的稳定笼型晶体包络物[1,2,3]。自然界的天然气水合物主要赋存于高压、低温的海洋大陆边缘和高纬度冻土区域的地层[4,5,6],是资源潜力最为巨大的非常规天然气能源,海域天然气水合物具有较好的商业开发前景,但是钻采难度大[7,8,9,10]。我国南海神狐海域天然气水合物储层以黏土质粉砂型和粉砂质黏土为主,黏土矿物含量为26% ~ 30%,主要成分为蒙脱石、伊利石、高岭石等[11,12]。黏土矿物因存在同构替换、离解以及吸附等作用使得其表面带负电荷[13],当其处于电解质溶液中,阳离子会积聚在黏土矿物表面形成双电层[14]。
HELMHOLTZ[15]首先提出双电层的平板电容器模型（H模型）,认为双电层类似于平板电容器,正负离子等量且整齐地排列在固液界面两侧,两层之间的距离约等于离子半径。以上H模型没有考虑溶液中离子的扩散、吸附等作用。GOUY[16]和CHAPMAN[17]对H模型进行了改进,提出了扩散双电层模型（GC模型）,考虑了正、负离子之间的静电吸引以及热运动,当两者平衡时反离子呈扩散状态分布于溶液中。GC模型将离子视为点电荷而忽略了离子自身的尺寸,也未考虑离子溶剂化所产生的影响。STERN[18]在改进GC模型的基础上提出了Gouy-Chapman-Stern（GCS）模型,该模型考虑了吸附在固体表面离子的尺寸,并将双电层分为斯特恩层（Stern层）与扩散层。黏土颗粒本身几乎不导电,但双电层的存在使得黏土颗粒表面具有导电性[19],且在低频电场作用下双电层产生电化学极化作用[20,21],因此双电层的特性成为影响黏土颗粒电学性质的关键因素。沉积物孔隙内天然气水合物的形成对黏土矿物颗粒表面双电层特性产生哪些影响尚不明确,该问题制约了对含水合物沉积物电学（如电化学、电磁学）性质的准确认识,成为基于宏观电学性质反演沉积物孔隙度、水合物饱和度和渗透率方法的瓶颈问题。
针对黏土矿物表面双电层的性质,国内外学者取得了一系列研究进展。SHANG等[22]提出了黏土-水-电解质系统双电层中定量测定电势分布的方法,利用GCS模型分析了影响黏土双电层电势分布的各种因素。TOURNASSAT等[23]基于分子动力学（molecular dynamics, MD）理论建立了蒙脱石与NaCl水溶液体系的数值模型,模型计算结果与修正的GC模型的理论进行了比较,结果表明MD模拟可以用于确定基本Stern模型的参数;BOURG等[24]利用MD模拟了混合电解质溶液（NaCl-CaCl2）中蒙脱石表面的双电层结构,证实了双电层存在三个不同的离子吸附面;ZHANG等[25]利用MD模型计算了蒙脱石表面强结合水（不能自由移动的水）的厚度,认为强结合水的边界位于双电层中最接近剪切面（不能自由移动的水层与流动流体之间的边界）的水层;尚飞等[13]基于GCS理论建立了黏土表面双电层结构的有限元数值模型,分析了温度、浓度、矿物类型等对黏土表面双电层电势分布的影响因素。在对黏土表面双电层特性进行研究的过程中,利用MD模拟可以显性地考虑系统中的每个原子,能够表征分子与离子的浓度分布,能够动态地观察到水合物的微观形成过程[7,26]、离子的吸附与扩散过程以及双电层内部的结构,但是其缺点在于无法将晶胞模型扩展到黏土矿物颗粒模型、无法计算宏观电场参数,而采用有限元（finite element, FE）数值模拟方法虽然不能考虑到水合物的形成过程、离子与分子的运动以及相互作用,但是可以建立黏土颗粒模型并计算其表面附近的电场参数。上述两种技术的联合对于研究沉积物孔隙中水合物对黏土颗粒表面区域电学特性的影响及其机理具有重要作用。
针对孔隙内水合物形成对黏土矿物表面区域电学特性影响的问题,本文提出利用MD与FE相结合的新思路,基于GCS理论建立无/含水合物-蒙脱石-NaCl溶液体系的MD和FE数值模型,探讨水合物的形成对蒙脱石表面双电层性质以及表面区域电势分布的影响规律及机理,提出有待进一步解决的问题。本研究可为深入认识含水合物泥质沉积物中骨架颗粒的电学特性、量化颗粒表面电性参数提供理论和模型基础。
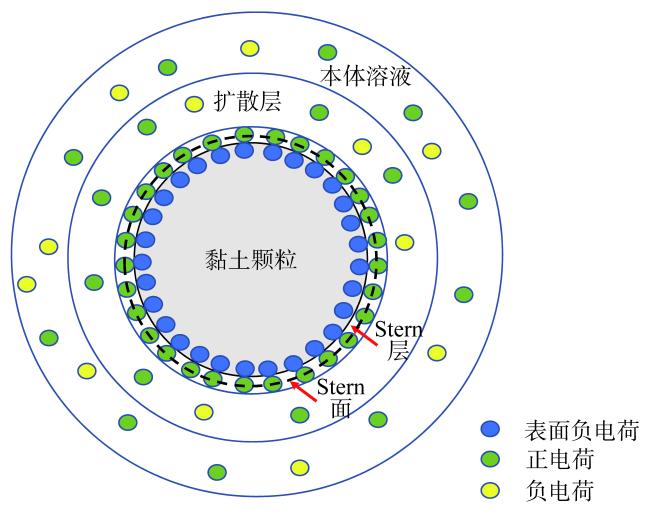
1 双电层基本理论
$\sigma =-\left( {{\sigma }_{1}}+{{\sigma }_{2}} \right)$ (1)
式中：σ为总电荷密度,C/m2;σ1为Stern层电荷密度,C/m2;σ2为扩散层电荷密度,C/m2。
Fig. 1 Structure of electrical double layer图1 双电层结构 |
${{\sigma }_{1}}=\frac{\ {{N}_{i}}\ zF}{\ \ 1+\frac{{{N}_{\text{A}}}\ \nu }{M{{c}_{\ 0}}}\ \ \exp \left( \ -\frac{zF{{\varphi }_\ \ {\text{d}}}\ \ +\phi }{RT}\ \ \ \ \right)\ \ \ \ }$ (2)
${{\sigma }_{2}}=\sqrt{8{{c}_{0}}{{\varepsilon }_{0}}{{\varepsilon }_{\text{m}}}RT}\sinh \left( \frac{zF{{\varphi }_{\text{d}}}}{2RT} \right)$ (3)
式中：Ni为单位面积上可吸附的离子点位数,m-2;i为离子序号;z为离子价态;F为法拉第常数,F = 9.648 7 × 104 C/mol;NA为阿伏伽德罗常数,NA = 6.02 × 1023;$\nu $为电解质溶液密度,kg/m3;M为溶剂的摩尔质量,kg/mol;c0为电解质中离子的摩尔浓度,mol/m3;φd为Stern电势,V;$\phi $为比附势,$\phi $ = 0;R为气体常数,R = 8.314 J∙mol-1∙K-1;T为绝对温度,K;ε0为真空介电常数,ε0 = 8.854 × 10-12 F/m;εm为扩散层的相对介电常数,F/m。假设扩散层溶液的相对介电常数与本体溶液相等[23]。
$\varphi (x)=\left\{ \begin{matrix} {{\varphi }_{0}}-\frac{{{\varphi }_{0}}-{{\varphi }_{\ \text{d}}}}{d}x\text{ }x\le d\text{,} \text{Stern 层} \\ \frac{2RT}{zF}\ln \left(\ \ \frac{{{\ \ \text{e}}^{\kappa \left( x-d \right)}}\ \ \text{+}\ \ \tanh \frac{zF{{\varphi }_{\ \ \text{d}}}}{4RT}}{{{\ \ \text{e}}^{\kappa \left( x-d \right)}}\ \ -\ \ \tanh \frac{zF{{\varphi }_{\ \text{d}}}}{4RT}} \ \ \right)\text{ }x>d, 扩散层 \\ \end{matrix} \right.\ \ \ \ \ $ (4)
式中：φ0为颗粒表面的电势,V;κ为德拜长度的倒数,m-1;d为Stern层的厚度,m;x为距黏土表面的距离,m。
根据电势在Stern层内随距离增长线性下降[22],可得到以下表达式计算颗粒表面的电势：
${{\varphi }_{\text{0}}}\text{=}{{\varphi }_{\text{d}}}+\frac{\sigma d}{{{\varepsilon }_{0}}{{\varepsilon }_{\text{d}}}}$ (5)
式中：εd为Stern层的相对介电常数,F/m。
${{\kappa }^{-1}}=\frac{1}{\sqrt{\frac{2{{c}_{\ 0}}\ {{z}^{2}}\ {{F}^{2}}}{{{\varepsilon }_{0}}\ {{\varepsilon }_{\ \text{w}}}\ RT}}}$ (6)
式中：εw为水的相对介电常数,F/m。
2 数值建模
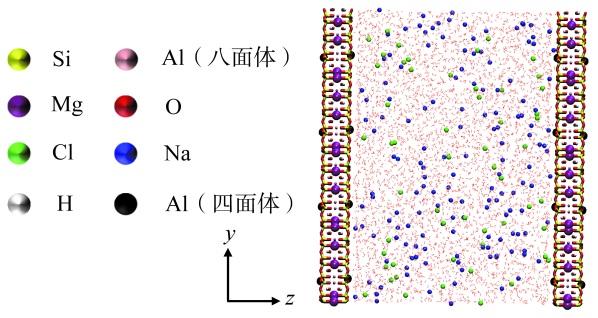
2.1 分子动力学模型
2.1.1 模型建立
蒙脱石具有典型的层状结构,具有与水分子和溶解离子相互作用的大的比表面积,是含水合物沉积物中广泛存在的主要黏土矿物。本研究以钠基蒙脱石为研究对象,其分子结构通常采用美国怀俄明州蒙脱石结构[31],分子式为Na0.75(Si7.75Al0.25)(Al3.5Mg0.5)O20(OH)4。蒙脱石具有2∶1型结构,即两个四面体片和一个八面体片[14]。本文所用蒙脱石模型是将黏土单胞沿x、y、z方向复制,合并为64（即8 × 8 × 1）个晶胞,最终的模型通过黏土矿物中阳离子的同构替换生成,即八面体片上的Al3+ 被Mg2+ 取代,四面体片上的Si4+ 被Al3+ 取代,致使蒙脱石带负电荷,黏土的表面电荷密度为 -0.26 C/m2。
首先,在黏土层孔隙中放置一个4.216 nm × 7.105 nm × 5 nm的水盒子,水盒子与黏土层表面的间隙为0.02 nm;然后,在水盒子中随机放置一定量的Na+ 补偿蒙脱石所引起的电负性;最后,在水盒子中填充质量分数为3.5%的NaCl,形成模拟地层孔隙水的溶液。通过上述步骤可构建出蒙脱石-NaCl溶液混合物模型,模型的几何结构在x、y、z方向上的尺寸为4.216 nm × 7.105 nm × 6.425 nm（图2）,其中放大的紫色小球表示Mg2+（八面体片上的Al3+ 被Mg2+ 取代）,黑色小球表示Al3+（四面体片上的Si4+ 被Al3+ 取代）。
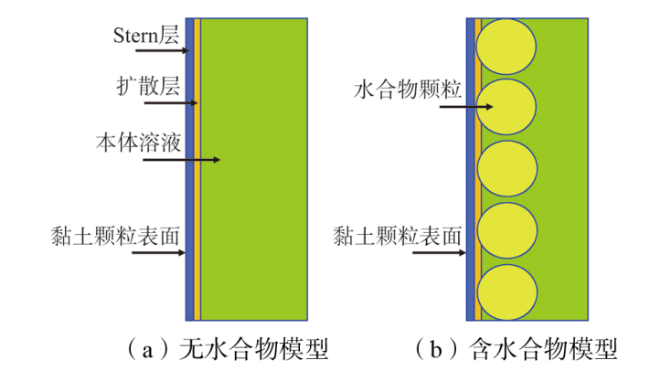
Fig. 2 Initial configuration of montmorillonite-NaCl solution mixture图2 蒙脱石-NaCl溶液混合物初始构型 |
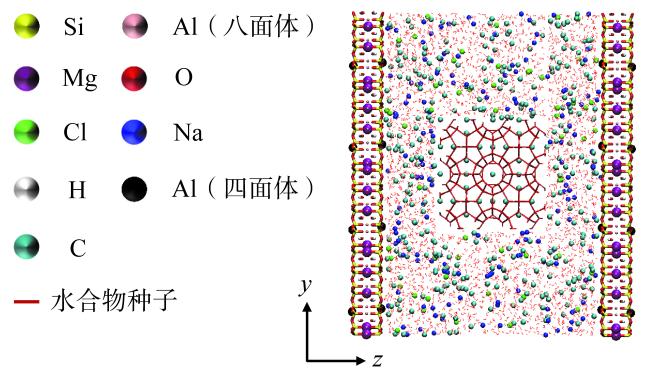
Fig. 3 Initial configuration of montmorillonite-NaCl solution-methane hydrate mixture图3 蒙脱石-NaCl溶液-甲烷水合物混合物的初始构型 |
2.1.2 模拟方法
在进行MD模拟之前,首先利用最速下降算法对系统进行能量最小化（energy minimization, EM）处理,设置能量步长为 0.01 nm,设置最大力的收敛准则为200 kJ∙mol-1∙nm-1。在截止长度为1.0 nm条件下计算范德华力和静电力的相互作用,采用快速光滑粒子网格Ewald方法计算傅里叶间距为0.12 nm的长程静电相互作用。设置温度为260 K,压力为10 MPa,在此热力学条件下甲烷水合物处于稳定状态[39]。将无水合物模型的模拟时间步长设置为1 fs,在等压等温系综中对系统进行300 ns的平衡及动力学模拟;将含水合物模型的模拟时间步长设置为2 fs,在等压等温系综中对系统进行1 000 ns的平衡及动力学模拟。使用Nosé-Hoover控温器和Parrinello-Rahman恒压器分别调节温度和压力。在模拟过程中,系统在各个方向满足周期性边界条件。系统压力采用半各向同性压力耦合,使得z方向、x/y方向的压力独立波动。为了避免蒙脱石层原子的漂移,设定蒙脱石层为刚性。
2.1.3 模拟数据处理方法
F4序参数用来统计水体系中两个相邻水分子最外侧氢原子以及水分子中氧原子组成的二面角,其计算公式如下：
${{F}_{4}}=\left\langle \cos 3{{\theta }_{n}} \right\rangle $ (7)
式中：θn为相邻两个水分子的氧原子与最外侧氢原子的二面角;n为二面角的序号。液态水F4的平均值为 -0.04,水合物与冰的F4平均值分别为0.7与 -0.4。
GCS模型考虑离子之间的相互作用及离子的热运动,离子呈扩散状态分布于溶液中,离子扩散系数可利用离子平均的均方位移（mean square displacement, MSD）的斜率[42]来计算：
$D=\underset{t\to \infty }{\mathop{\lim }}\,\frac{\partial }{\partial t}\frac{\left\langle {{\left| r(t)-r(0) \right|\ \ }^{2}} \right\rangle }{6}$ (8)
式中：D为离子扩散系数,m2/s;r(t) 表示笛卡尔空间中连续的粒子轨迹。
2.1.4 模型验证
根据无水合物模型数据来分析沿z轴方向的离子数密度分布（图4）。据文献[27],Stern层的厚度近似为水合离子的半径。扩散层是指Stern层外围起直到溶液浓度均匀为止（${{c}_{\text{N}{{\text{a}}^{\text{+}}}}}={{c}_{\text{C}{{\text{l}}^{-}}}}$）的部分。扩散层的Na+ 以玻尔兹曼规律分布,扩散层的起点为Na+ 数密度分布（图4）中距蒙脱石表面的第二个峰值处,此处同时也是Stern层的外边界。水合Na+ 的半径为0.36 nm[43],则Stern层的厚度约为0.36 nm。根据公式（6）得出扩散层的理论估计值为0.70 nm。分析图4可知MD模拟得到的双电层厚度（表1）与理论估计值接近。根据表1可知,左右两侧黏土层的Stern层厚度存在差异,分析其原因为：MD数值模拟过程中,受界面影响的离子序号具有一定的随机性;统计离子数密度的过程中涉及对模拟区域的分割,即沿z轴将体系划分为宽度为0.064 nm的薄片区域,Stern层厚度量化的空间分辨率为0.064 nm（两侧黏土层的Stern层厚度相差0.10 nm,与分辨率接近）。
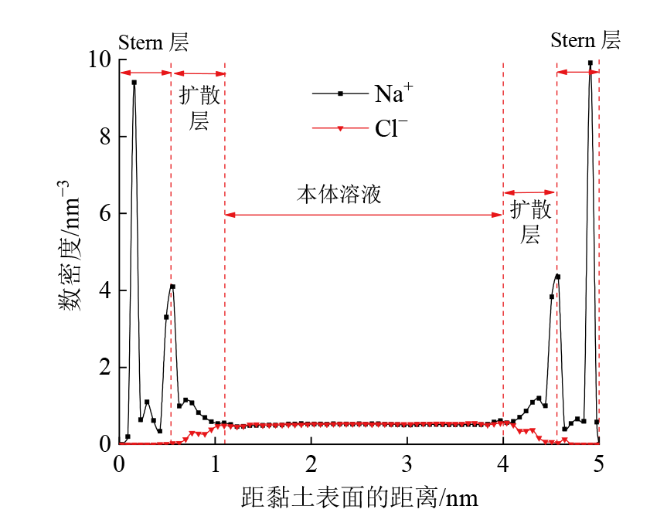
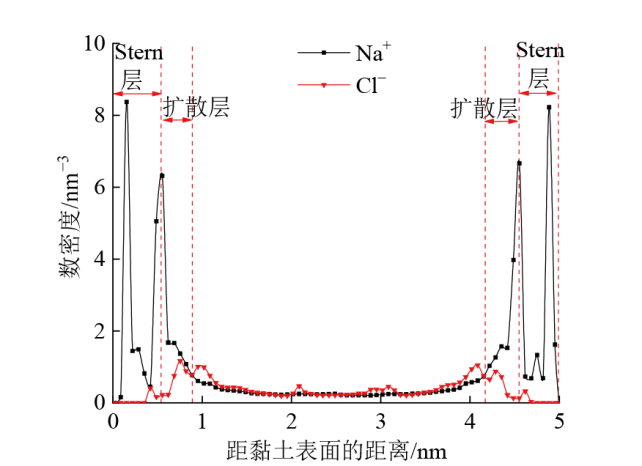
Fig. 4 Number density distribution of ions along the z direction in the hydrate-free model图4 无水合物模型中离子数密度沿z轴方向的分布 |
Table 1 Thickness of electrical double layer in hydrate-free model表1 无水合物模型的双电层厚度 |
| 电层 | 理论估计值/nm | 左侧黏土层/nm | 右侧黏土层/nm |
|---|---|---|---|
| Stern层 | 0.36 | 0.54 | 0.44 |
| 扩散层 | 0.70 | 0.56 | 0.56 |
2.2 有限元数值模型
2.2.1 几何结构与材料
图5为有限元数值模拟所采用的几何结构,分别是无水合物模型与含水合物模型。MD结果表明水合物与黏土颗粒之间的距离不小于0.5 nm,水合物不会影响Stern层结构,但会侵占部分扩散层,因此在构建含水合物有限元数值模型时设定水合物与黏土颗粒表面之间的距离不小于0.5 nm。蒙脱石粒径设置为2 μm,整个模型的尺寸为0.5 μm × 2 μm。
Fig. 5 Two-dimensional geometric structure of electrical double layer on the surface of montmorillonite图5 蒙脱石表面双电层的二维几何结构 |
2.2.2 静电场/稀物质传递控制方程
基于GCS理论建立黏土颗粒表面双电层有限元数值模型,采用泊松方程描述电荷密度与电场,GCS模型考虑了离子扩散,则通过联立Nernst-Planck方程实现,该方程描述了体系内离子的扩散与质量传递。通过联立泊松方程与Nernst-Planck方程可以准确模拟离子与电场的相互作用,因此双电层可视为泊松方程与Nernst-Planck方程的耦合[45]。
多物理场耦合计算平台COMSOL Multiphysics内置了Nernst-Planck-Poisson（NPP）物理场控制方程,该方程与扩散双电层的控制方程一致,NPP模块是静电场模块与稀物质传递模块多物理场相耦合。因此采用COMSOL Multiphysics平台建立上述数值模型。
泊松方程的数学形式为：
$\nabla \cdot \left( -\varepsilon \nabla \varphi \right)=\sigma $ (9)
式中：ε为介电常数,F/m;σ为空间电荷密度,C/m3。
Nernest-Planck方程数学形式为：
${{J}_{i}}=-{{D}_{i}}\nabla {{c}_{i}}-{{u}_{\text{m},i}}{{z}_{i}}F{{c}_{i}}\nabla \varphi $ (10)
式中：Di为扩散系数,m2/s;um,i为迁移率,s∙mol/kg。
在静电场模块中,联立式（1）~ 式（3）求得表面电荷密度σ1与σ2分别为0.202 C/m2和0.055 C/m2,将其分别赋值于蒙脱石颗粒表面与Stern面。在稀物质传递模块中,设置黏土颗粒表面为离子无通量界面,溶液浓度为0.61 mol/L（NaCl质量分数为3.5%）。根据MD得到离子的扩散系数赋值于物理场中。在距离颗粒表面足够远处电解质溶液浓度达到平衡。通过在两个模块中施加上述边界条件对控制方程（9）、（10）进行数值求解,可得到黏土颗粒表面附近的电势分布。
2.2.3 网格剖分与数值求解
有限元模型网格剖分直接影响到数值结果的准确性以及模型求解所占的时间与存储空间。利用模型解的网格依赖性来获取适当的网格数量。采用自由三角形网格将计算区域进行离散化,通过并行稀疏直接法（multi-frontal massively parallel sparse direct solver, MUMPS）进行求解。
以无水合物模型为例,黏土颗粒表面电势与Stern电势随网格数量变化的曲线如图6所示。Stern电势与颗粒表面电势随网格数量的增加而趋于稳定,为减少计算成本,选择网格数量为433 598的网格进行后续的数值计算。
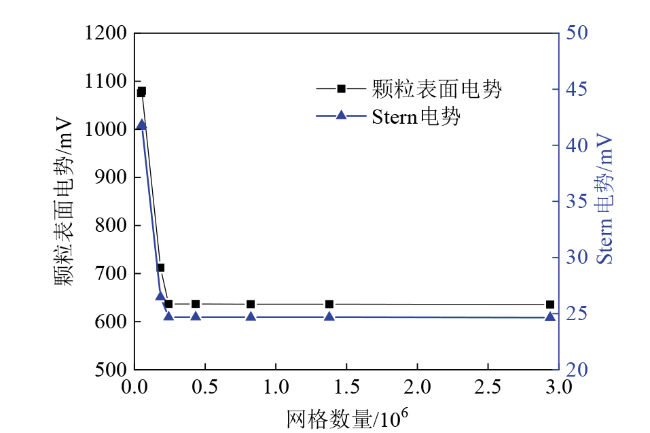
Fig. 6 Variation curves of the surface potential of clay particle and Stern potential with the number of grids图6 黏土颗粒表面电势与Stern电势随网格数量变化曲线 |
2.2.4 模型验证
图7是将公式（4）计算得到理论值与有限元模型对比进行模型验证,分析可知Stern层内的电势分布偏差较大（但变化趋势一致）,推测原因可能是将黏土颗粒看作了一个平面并且忽略了离子尺寸,将原本Stern层和扩散层的表面电荷密度赋值到了黏土颗粒表面与Stern面,导致Stern层内电势偏差大。扩散层内的电势分布是一致的。在Stern层内,电势在黏土颗粒表面取最大值,近似线性地下降到Stern电势,在扩散层内遵循指数型下降规律一直到0。
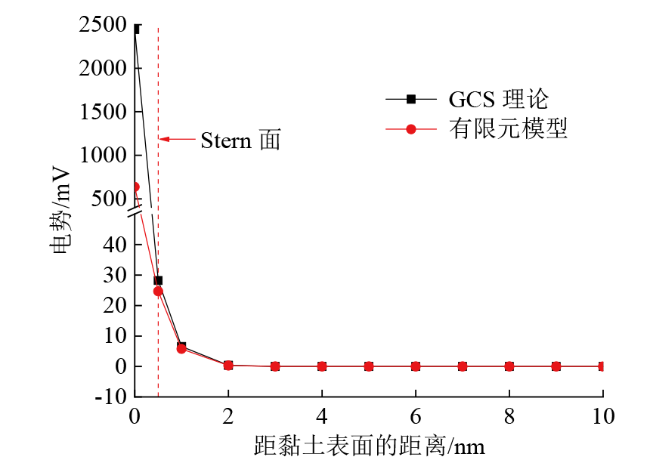
Fig. 7 Comparison of potential distribution between GCS theory and finite element model图7 GCS理论与有限元模型的电势分布对比 |
3 结果分析
3.1 数值模拟中水合物的形成
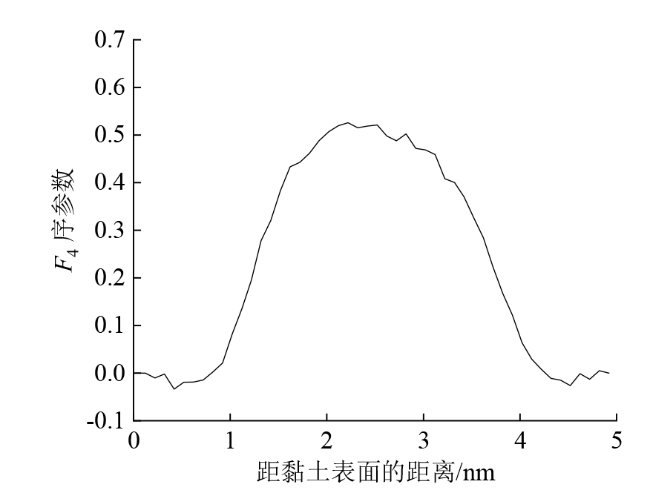
Fig. 8 Variation trend of F4 order parameter along the z direction图8 F4序参数沿z轴方向的变化趋势 |
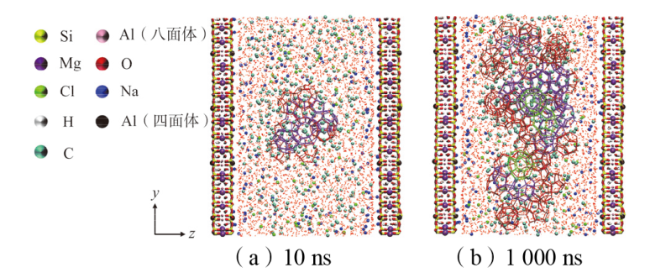
Fig. 9 Growth process of hydrate图9 水合物生长过程 |
3.2 双电层结构和离子扩散系数
Fig.10 Number density distribution of ions along the z direction in the hydrate-bearing model图10 含水合物模型中离子数密度沿z轴方向的分布 |
Table 2 Thickness of electrical double layer in hydrate-bearing model表2 含水合物模型的双电层厚度 |
| 电层 | 左侧黏土层/nm | 右侧黏土层/nm |
|---|---|---|
| Stern层 | 0.54 | 0.45 |
| 扩散层 | 0.35 | 0.33 |
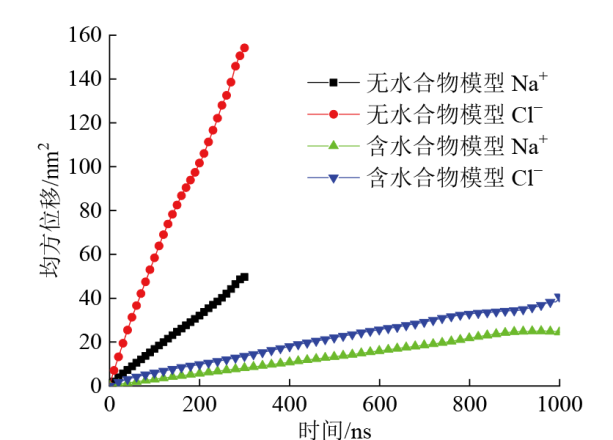
Fig. 11 Curve of ions mean squared displacement variation with time图11 离子的均方位移随时间变化曲线 |
Table 3 Diffusion coefficients of ions表3 离子的扩散系数 |
| 模型 | ${{D}_{\text{N}{{\text{a}}^{\text{+}}}}}$/(m2/s) | ${{D}_{\text{C}{{\text{l}}^{-}}}}$/(m2/s) |
|---|---|---|
| 无水合物 | 2.6 × 10-11 | 7.7 × 10-11 |
| 含水合物 | 4.3 × 10-12 | 6.5 × 10-12 |
3.3 双电层内电势分布
上述MD模拟的结果表明水合物的形成影响离子的扩散特性,影响双电层的厚度且水合物侵占部分扩散层区域。由电磁场基本理论可知黏土矿物表面附近的电势分布特性会受到直接影响,从而引起黏土颗粒表面电学特性的变化。图12为利用无/含水合物体系的有限元数值模型得到的黏土颗粒表面区域电势分布云图。分析图12可知：平均电势随黏土颗粒表面距离的增大而逐渐降低;水合物的存在导致蒙脱石颗粒表面附近区域的电势呈现出不均匀分布。分析其原因为：Stern层的电荷密度比扩散层的电荷密度高,则颗粒表面电势最高,随着与颗粒表面之间距离的增加,溶液中的阴阳离子逐渐趋向平衡,电势逐渐降低[47];水合物对扩散层的侵占使得扩散层部分区域的相对介电常数发生变化,从而引起该区域中电势的非均匀分布。
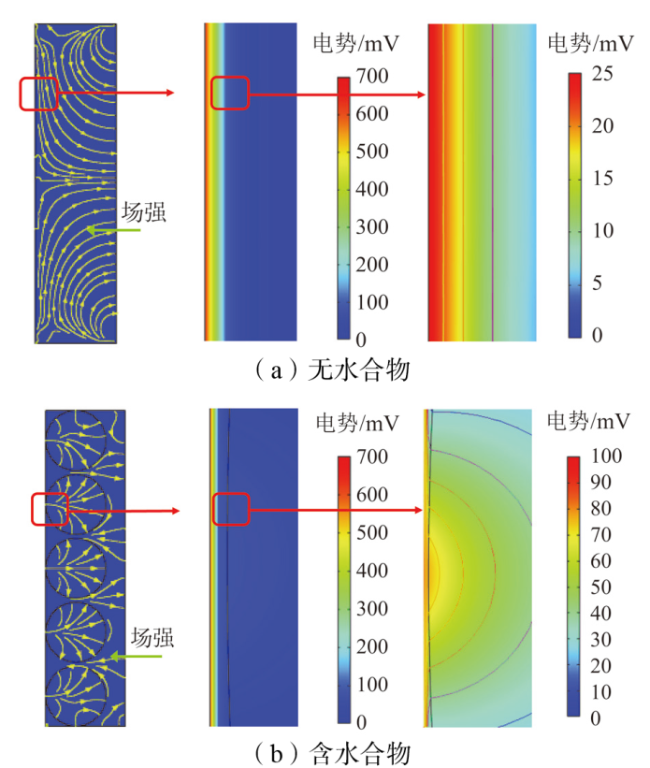
Fig. 12 Cloud images of potential distribution in hydrate-free system and hydrate-bearing system图12 无水合物体系与含水合物体系的电势分布云图 |
图13对比了无水合物与含水合物体系中的黏土颗粒表面附近区域的平均电势,图14对比了含水合物体系中的无水合物区域和含水合物区域的平均电势分布。结合图12对图13、图14进行分析可知：在含水合物的条件下,从左到右双电层的平均电势变化趋势与无水合物体系相一致,而从上到下的电势分布因水合物的存在而与无水合物体系差异较大;水合物的存在不影响Stern层内的电势分布,但会引起扩散层内平均电势的升高。分析其原因为：从MD模拟结果可知水合物不影响Stern层而仅侵占扩散层的部分区域,Stern层的相对介电常数也未发生变化,因此Stern层电势无明显变化;MD模拟结果表明水合物的形成使得扩散层厚度减小,根据公式（4）可知,电势与扩散层厚度之间关系密切,扩散层厚度的减小引起电势的升高;水合物的相对介电常数小于扩散层溶液的相对介电常数,水合物侵占扩散层部分的相对介电常数变小,因此电势有所升高[13,20]。
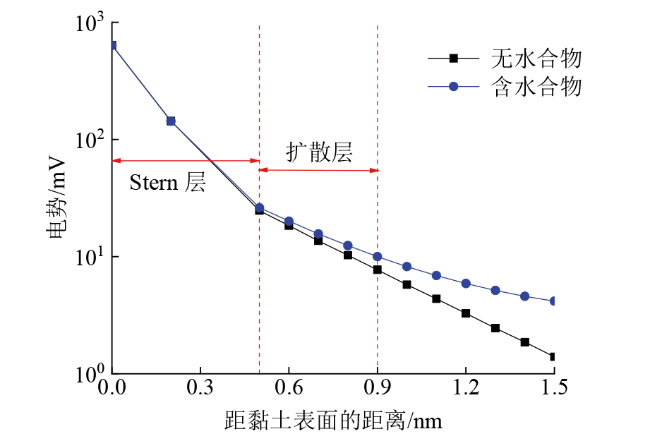
Fig. 13 Comparison of average potential distribution near the surface of clay particle in hydrate-free system and hydrate-bearing system图13 无水合物体系与含水合物体系中黏土颗粒表面附近的平均电势分布对比 |
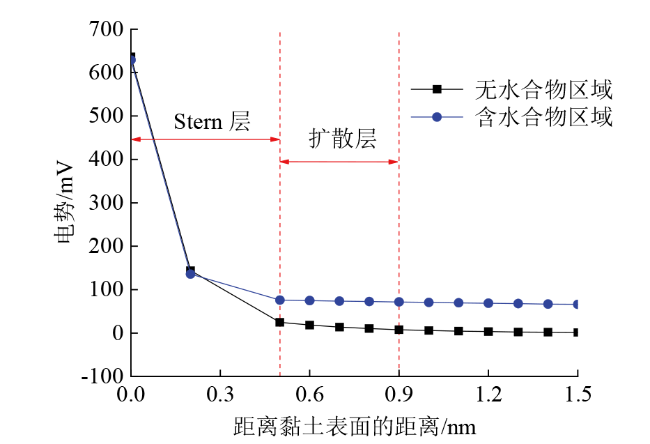
Fig. 14 Average potential distribution in the hydrate-free region and hydrate-bearing region of the hydrate-bearing system图14 含水合物体系中无水合物区域和含水合物区域的平均电势分布 |
依据上述MD的模拟结果,含水合物体系的双电层厚度约为0.83 nm,且水合物与黏土表面之间的距离不小于0.5 nm。图15展示了水合物在不同位置（相对于黏土颗粒表面）时黏土颗粒表面附近的平均电势分布。分析图15可知,随着水合物颗粒与黏土颗粒表面距离的增大,平均电势逐渐降低。平均电势的变化主要由该区域相对介电常数的变化所引起[20]。随着水合物与黏土颗粒表面距离的增加,水合物侵占扩散层的体积逐渐减少,扩散层的介电常数逐渐升高（因水合物的介电常数低于溶液）。另外,双电层的电导率可通过电势分布进行量化计算[29],可见水合物与黏土颗粒之间的距离因影响电势分布而影响双电层的电导率,即颗粒的表面电导特性。
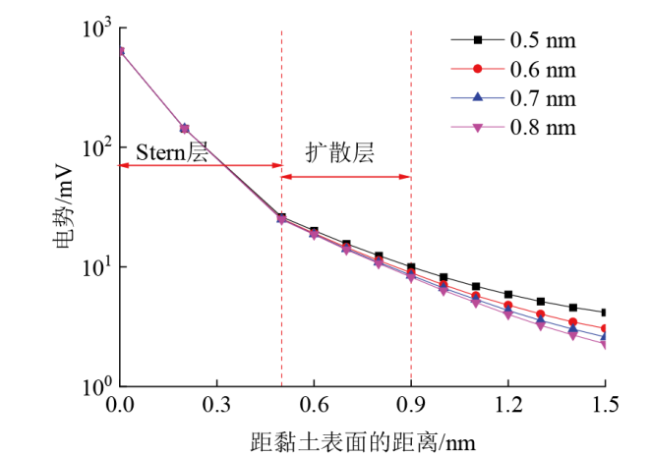
Fig. 15 Average potential distribution near the surface of clay particles with the hydrate at different positions图15 水合物在不同位置时黏土颗粒表面附近的平均电势分布 |
4 讨论
4.1 模拟结果的潜在应用
通过分子动力学模拟认识到蒙脱石表面与水合物之间不直接接触,两者之间存在厚度可知的Stern层,因此在建立含水合物多孔介质数值模拟时应考虑如何处理水合物与骨架颗粒之间的相对位置关系,该相对位置关系对含水合物沉积物电学、声学、热学、力学、水力学的性质产生重要影响。
通过分子动力学模拟认识到水合物生长后侵占部分扩散层但不影响Stern层,该认识有助于将来深入探讨低频交变电场作用下含水合物沉积物的导电和激发极化特性,从而为改进水合物饱和度与电学参数（导电和介电参数）之间的关系模型提供理论基础。
通过有限元模拟认识到蒙脱石表面区域电势的分布特性,电势分布特性蕴含了该区域内具有不同电导率和介电常数物质（如水合物、束缚水、自由水）的空间分布信息,这为改进含水合物沉积物的电学特性模型（电阻率、介电常数响应模型）和基于电学参数的水合物饱和度模型提供理论基础。
综上所述,在含水合物沉积物电学特性研究中,双电层的作用主要体现在颗粒表面的导电性以及低频交变电场作用下的双电层极化。深入研究水合物形成对黏土矿物表面双电层以及表面区域电学特性的影响,有助于从微观层面、理论层面认识颗粒表面导电性及极化特性的变化规律,从而为基于电学参数（电阻率、介电常数、激发极化参数等）反演水合物饱和度模型的建立和优化提供理论基础。
4.2 不同类型的黏土矿物
4.3 黏土颗粒表面电学特性
5 结论
提出分子动力学（MD）与有限元（FE）数值模拟相结合的新方法,利用所建立的无/含水合物-蒙脱石-NaCl溶液体系的数值模型探讨了甲烷水合物形成对蒙脱石表面双电层性质和表面区域电势分布的影响规律及机理,得到以下结论：
（1）利用MD模型可获得含水合物条件下蒙脱石表面双电层中Stern层和扩散层的厚度以及溶液中离子的扩散系数,为FE模型提供双电层结构参数与离子运动参数,基于FE模型可分析蒙脱石表面区域电势分布特性。
（2）蒙脱石表面形成稳定致密的钠离子层与界面水层,甲烷分子无法在蒙脱石表面生成水合物,因此水合物不影响Stern层而侵占部分扩散层区域;水合物形成过程中“排盐效应”使溶液中的盐离子浓度增大,对扩散层中Na+ 产生排斥作用,使扩散层中的部分Na+ 进入Stern层,导致扩散层变薄;水合物的生长降低了溶液中离子的扩散系数。
（3）水合物对扩散层的侵占使得扩散层部分区域的相对介电常数发生变化,引起该区域中电势的非均匀分布;水合物的存在不影响Stern层内的电势分布,但被水合物侵占的扩散层部分相对介电常数变小,引起扩散层内平均电势的升高;随着水合物与黏土颗粒表面距离的增加,平均电势逐渐降低。
