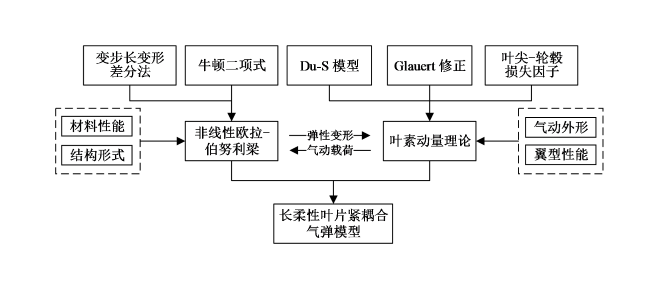
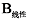梁理论和三维有限元方法(finite element method, FEM)分别具有计算效率高和仿真精度好的特点,因此在进行考虑气弹耦合效应的叶片气动结构一体化设计时多采用这两种方法。王永志等
[1]基于叶素动量(blade element momentum, BEM)理论耦合FEM,以叶片气动和结构性能为约束,以质量最小为目标,采用多岛遗传算法对风力机叶片的叶根、盒型梁、前缘梁、尾缘梁、弦长、扭角等参数进行优化设计,初步提出了复合材料风力机叶片的气动-结构一体化优化设计方法。KESHAVARZZADEH等
[2]通过耦合BEM理论和FEM改进了一种考虑来流风不确定性的叶片优化设计方法。THAPA等
[3]采用BEM理论耦合FEM的方法,在叶尖挠度、固有频率等约束条件下,对叶片的弦长、扭角和材料铺层参数展开了叶片质量最小与年发电量最大的两目标优化。上述FEM方法虽然提高了气弹仿真模型的计算精度,获得了更加精确的叶片设计结果,但受限于算法计算速度和集成开发难度,在工程实践中难以推广。基于梁理论的气弹仿真模型
[4]计算速度更快、易于集成开发,且具有良好的普适性。郑玉巧等
[5]基于BEM理论与线性梁理论建立了叶片静气弹耦合分析模型,并采用遗传算法对叶片弦长、扭角与铺层厚度展开了叶片质量最小的单目标优化,实现了1.2 MW机型叶片的降本增效设计。郭小峰等
[6,7]提出了叶片预弯型线设计方法,以GH Bladed气弹仿真模型为核心,采用MATLAB构建了预弯叶片的气动外形和铺层结构一体化优化设计模型,并采用粒子群算法优化得到可满足主机不同匹配需求叶片的Pareto最优解集。风力机叶片的大型化使叶片柔度与弹性变形引起的几何非线性不断增强,气弹耦合分析愈发被重视
[8,9,10],“BEM理论 + 线性梁”已无法满足长柔性叶片气弹仿真精度的需求。“BEM理论 + 几何精确梁”能够考虑长柔性叶片结构的非线性特性,其在气弹仿真建模中的应用已较为成熟
[11,12]。然而,由于其复杂度且计算速度较慢,在耦合多目标优化模型的应用仍很少见。
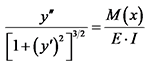
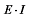 为梁的抗弯刚度;M (x)为弯矩。
为梁的抗弯刚度;M (x)为弯矩。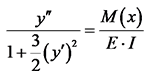
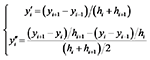
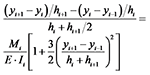
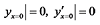 ,由于
,由于 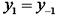 ,令
,令 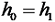 ,则有
,则有 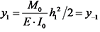 。令
。令 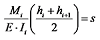 ;
; 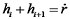 ;
; 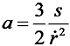 ;
; 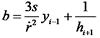 ;
; 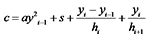 。式(4)可化为
。式(4)可化为 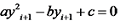 ,得到
,得到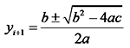
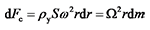
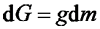
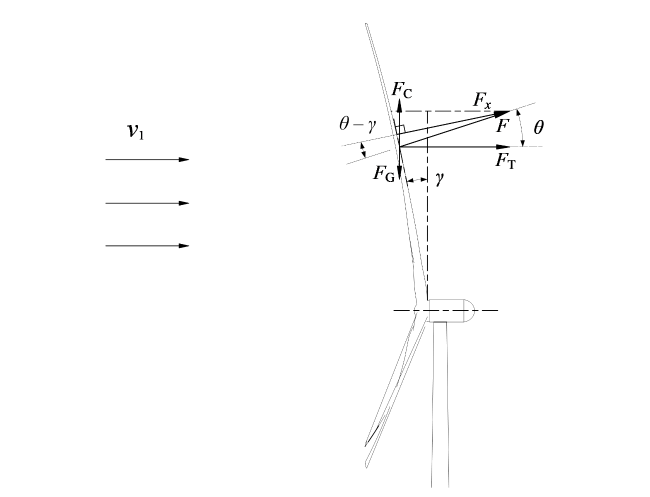
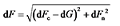 ,Fn由BEM理论计算得到,dF与水平轴线的夹角
,Fn由BEM理论计算得到,dF与水平轴线的夹角 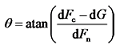 。风力机的叶片挥舞载荷
。风力机的叶片挥舞载荷 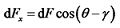 ,其中
,其中 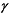 为叶片锥角。该叶素段对叶根的挥舞弯矩
为叶片锥角。该叶素段对叶根的挥舞弯矩 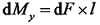 ,力臂
,力臂 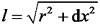 ,dx为该叶素控制点到变桨轴线的变形量。
,dx为该叶素控制点到变桨轴线的变形量。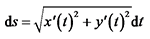
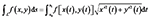
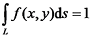 ;
; 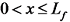 ,即x0 = 0,x1 = Lf;可求得风轮缩放因子Lf的数值解。
,即x0 = 0,x1 = Lf;可求得风轮缩放因子Lf的数值解。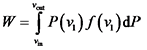
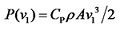 ;Cp为风能利用系数;ρ为空气密度,kg/m3;A为实际扫风面积,
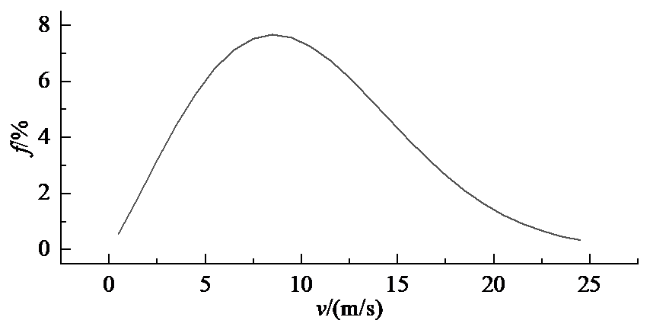
;Cp为风能利用系数;ρ为空气密度,kg/m3;A为实际扫风面积, 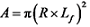 ;f (v1)为给定风场Weibull分布风速概率密度函数(见图2)。
;f (v1)为给定风场Weibull分布风速概率密度函数(见图2)。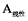
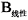
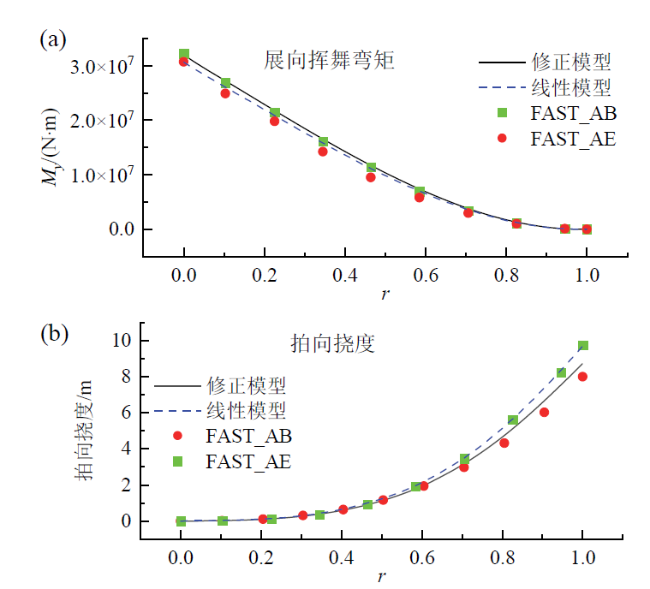
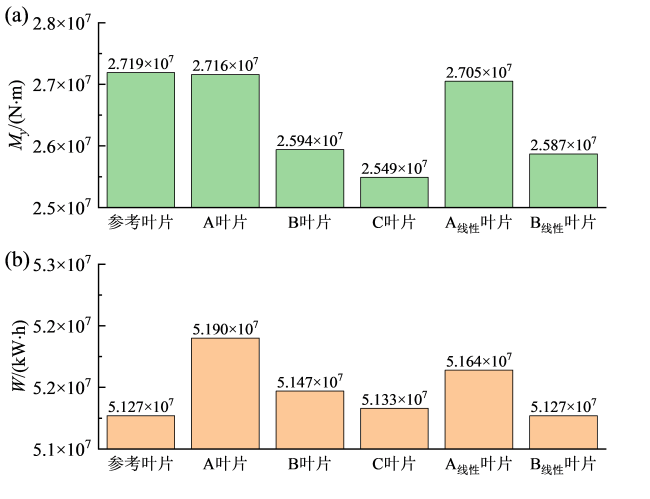
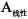 、叶片B与叶片
、叶片B与叶片 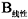 ,发现在同等载荷情况下,非线性优化得到的叶片单机年发电量更大。叶片C相较于叶片
,发现在同等载荷情况下,非线性优化得到的叶片单机年发电量更大。叶片C相较于叶片 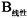 ,尽管载荷较小,其单机年发电量反而更大。
,尽管载荷较小,其单机年发电量反而更大。