欢迎访问《新能源进展》官方网站！今天是

新能源进展 >

2025 , Vol. 13 >Issue 1: 97 - 106

DOI: https://doi.org/10.3969/j.issn.2095-560X.2025.01.012

废风电叶片回收增强纤维的工艺与参数优化

  • 王程浩 1, 2 ,
  • 朱峰 3 ,
  • 陈德珍 , 1, 2, † ,
  • 洪鎏 1, 2
展开
  • 1 同济大学 热能与环境工程研究所，上海 200092
  • 2 上海市多源固废协同处理和能源化工程技术研究中心，上海 200092
  • 3 苏州天顺复合材料科技有限公司，江苏 常熟 215500
†陈德珍，E-mail：

王程浩（2000-），男，硕士研究生，主要从事城市固体废弃物热解研究。

陈德珍（1969-），女，博士，教授，博士生导师，主要从事固体废弃物热处理与资源化研究。

收稿日期: 2024-09-06

  修回日期: 2024-11-10

  网络出版日期: 2025-02-28

基金资助

上海市“科技创新行动计划”碳达峰碳中和专项项目(22dz1208200)

收起

Recycling Reinforced Fibers from Waste Wind Turbine Blades: Process and Parameter Optimization for Improving Mechanical Strength of the Fiber

  • Chenghao WANG 1, 2 ,
  • Feng ZHU 3 ,
  • Dezhen CHEN , 1, 2, † ,
  • Liu HONG 1, 2
Expand
  • 1 Thermal and Environmental Engineering Institute, Tongji University, Shanghai 200092, China
  • 2 Shanghai Engineering Research Center of Multi-source Solid Wastes Co-processing and Energy Utilization, Shanghai 200092, China
  • 3 Titan Wind-Composite Co. Ltd., Changshu 215500, Jiangsu, China

Received date: 2024-09-06

  Revised date: 2024-11-10

  Online published: 2025-02-28

Fold

摘要

风能在可再生能源体系中扮演着重要的角色，但随着废风电叶片数量逐年增加，废风电叶片的回收利用刻不容缓。利用热解法回收风电叶片中的增强纤维具有减容减量快、资源化程度高的优点，已有的研究主要针对碳纤维为增强纤维的情况，回收玻璃纤维的研究很少。玻璃纤维的强度受处理温度的影响较大，为提高玻璃纤维强度、降低能耗，采用热解−氧化脱碳工艺回收增强玻璃纤维，针对脱碳过程中的三个关键工艺参数即脱碳温度、保温时间、升温速率进行优化，基于响应曲面法设计实验，以回收的玻璃纤维的力学强度（最大荷重）为响应值，探究三个工艺参数对最大荷重的交互影响，实现回收的纤维具有最高强度。结果表明：脱碳温度对最大荷重的影响最为显著，保温时间和升温速率对最大荷重也有一定的影响。优化后的最佳工艺参数为脱碳温度452.45 ℃、保温时间43.20 min、升温速率11.12 ℃/min。实验也证实了优化后回收的纤维强度是最高的，可达到原始强度的51.2%，且优化的工艺参数对应的过程更节能。

关键词： 废风电叶片; 热解; 增强纤维回收; 氧化脱碳; 响应曲面法; 最大荷重

本文引用格式

王程浩 , 朱峰 , 陈德珍 , 洪鎏 . 废风电叶片回收增强纤维的工艺与参数优化[J]. 新能源进展, 2025 , 13(1) : 97 -106 . DOI: 10.3969/j.issn.2095-560X.2025.01.012

Abstract

Wind energy plays a crucial role in the renewable energy system. However, as the number of discarded wind turbine blades increases annually, recycle ing and utilizing these blades has become an urgent necessity. The pyrolysis-oxidation treatment of wind turbine blades has the advantages of reducing volume and recycling reinforced fiber from the blades. While research on recovering carbon fiber when used as reinforced fiber is available, few research pays attention to recycling glass fiber. To improve the mechanic strength of the recovered glass fiber and reduce energy consumption in this process, in this paper, key parameters in the pyrolysis-oxidation process, including the decarburization temperature, holding time, and heating rate, are optimized based on the response surface method with the fracture load of the recycled glass fiber as the response value to achieve the best mechanical properties of the recycled fiber, and the interaction between the three key parameters was also explored. The results show that the decarburization temperature plays most significant role in the fracture load, and the holding time and heating rate also play the important roles in the fracture load. The optimized process parameters are a decarburization temperature of 452.45 °C, a reaction time of 43.20 min, and a heating rate of 11.12 °C/min. The experimental results proved that those values are most suitable; the fracture load of the recycled fiber obtained after optimization achieved 51.2% of the new material, and the optimized process is more energy effective.

Key words： waste wind turbine blades; pyrolysis; reinforced fiber recycling; oxidative de-carbonization; response surface method; fracture load

0 引言

随着化石能源枯竭、生态环境污染等问题的加重，世界各国都在大力发展可再生能源。风能迎来了历史性的发展机遇[1]，在我国未来能源体系中扮演着至关重要的角色[2-3]。根据全球风能理事会的全球风能报告[4]，2023年全球风力发电累计装机总量增长至906 GW。风电的快速发展伴随着风电叶片的大量使用[5]，而风电叶片的设计使用寿命为20 ~ 25年[6]，因此未来几十年将有大量的废弃叶片等待处理[7]。
目前投入使用的风机叶片材料主要为玻璃纤维增强复合塑料和碳纤维增强复合塑料，增强纤维和以环氧树脂、聚酯树脂为代表的热固性树脂是风机叶片的主要组成部分[8-9]。而作为主要成分的环氧树脂在固化成形时，分子链发生不可逆的化学交联[10]，因此不易降解，废弃后也难以循环利用。
废弃风机叶片的回收方法包括焚烧处理、机械处理、化学溶解、热解处理等[11]。其中热解法不仅可以回收废风机叶片中的玻璃纤维或者碳纤维，热解后产生的油、气还可作为能源利用，具有减容、减量和资源化等优点[12]。
最大限度地保留增强纤维的机械强度十分重要。热解回收的增强纤维表面附着有热解炭，会降低与环氧树脂的附着力，影响回收纤维的利用[5]。因此在热解后应在空气下加热脱碳。然而，脱碳过程的工艺参数对回收纤维的性能有很大影响，高温脱碳可能会导致纤维强度的退化[13]。KIM等[14]先在过热水蒸气气氛下对碳纤维增强塑料进行热解，然后在O2/N2混合气氛中进行脱碳，回收碳纤维的拉伸强度保留了原始值的90%，然而该过程需要消耗水蒸气且仅对耐温高的碳纤维进行了实验。GIORGINI等[15]研究了玻璃纤维在不同氧化温度下所需脱碳时间，发现高温条件下脱碳所需时间更短。MEYER等[16]通过优化热解和脱碳过程中的温度和停留时间，得到拉伸强度保留率为96%的碳纤维。显然合理的工艺参数如温度、保温时间、升温速率可以最大限度地保留增强纤维的强度。但是，由于玻璃纤维价格低，回收的经济效益差，因此目前的相关研究主要针对碳纤维，针对回收玻璃纤维的研究较少，而废弃叶片中用玻璃纤维增强的更多，且玻璃纤维的强度比碳纤维更容易受温度的影响，如何能最大限度地保留玻璃纤维的强度，提高玻璃纤维回收的经济效益就更为重要。由于脱碳过程工艺参数（脱碳温度、保温时间、升温速率、氧分压等）对纤维强度的影响极其复杂，脱碳工艺参数优化困难。目前对脱碳工艺的优化缺乏科学全面的研究，对热解−微氧化过程的各个参数的影响和正确配置缺乏相关指导。
响应曲面法（response surface methodology, RSM）是一种基于多元统计学的优化方法[17]，通过多元回归方程，建立影响因子与响应值之间的函数关系，相比于其他优化方法，该方法实验次数少，省时经济，同时可通过3D曲面直观观察各因素与响应值之间的变化关系[18]。
本文基于响应曲面法，在热解以后，以脱碳过程中的升温速率、脱碳温度和保温时间为自变量，以回收玻璃纤维最大荷重即断裂时的拉力值为因变量，建立二次响应模型，讨论三种影响因子包括升温速率、脱碳温度和保温时间的显著性及交互作用影响，以得到最佳脱碳工艺参数，提升回收玻璃纤维强度，为相关回收工程实践奠定基础。

1 材料与方法

1.1 实验样品

实验采用的风机叶片材料为苏州天顺复合材料科技有限公司提供的玻璃纤维增强塑料型风机叶片，其中环氧树脂为树脂含量21%的双酚A型环氧树脂，玻璃纤维为欧文斯科宁公司的高模量玻璃纤维WindStrand4000（WS4000）。将风机叶片切成30 mm × 50 mm × 2 mm的长方体薄片状，以进行后续实验。叶片样品工业分析结果如表1所示。风机叶片灰分含量极高，挥发分和固定碳含量较少。
表1 叶片样品的工业分析（干燥基）

Table 1 Proximate and ultimate analysis of blade sample (dry basis)

组分 含量/%
灰分 83.34
挥发分 15.55
固定碳 1.11

1.2 热重实验及纤维性能测试

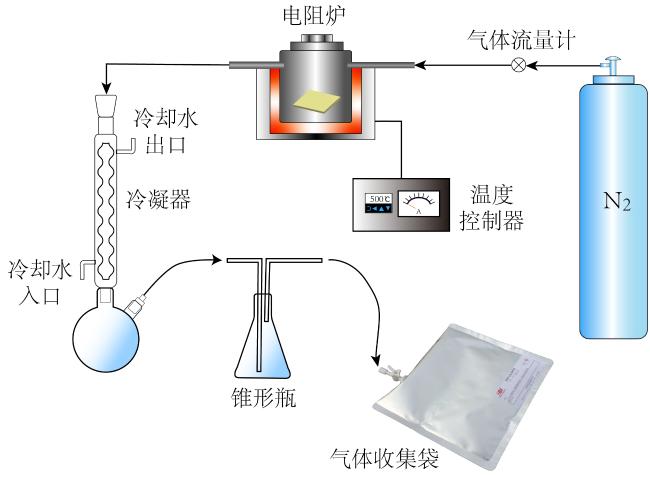
采用热重分析仪（thermogravimetric analyzer, TGA）（上海精科实业有限公司，TGA-1000型）考察样品的失重情况。称取约80 mg的风机叶片碎片，以10 ℃/min的升温速率，分别在氮气和空气气氛下（气体流量均为50 mL/min）测定风机叶片在0 ~ 800 ℃的失重情况。
对于每组试验点获得的纤维以及WS4000型原纤维，在电子万能试验机（上海协强仪器制造有限公司，CTM型）中进行拉伸试验，依据标准ASTM-D2343-17(2023)[19]，夹具移动速度设置为10 mm/min，针对等质量（0.01 g）的纤维测量断裂前最大荷重，为防止玻璃纤维样品不均匀，每个样品测量8次，取均值。

1.3 热解及脱碳实验

热解装置如图1所示，热解过程以N2为载气，以升温速率10 ℃/min加热到终温450 ℃并维持该温度30 min。
图1 热解装置示意图

Fig. 1 Schematic diagram of pyrolysis device

热解产生的气体使用气体采样袋收集，并采用气相色谱仪（美国安捷伦公司，7820型）测定成分；冷凝装置中收集到的液体产物采用气相色谱−质谱联用仪（gas chromatography-mass spectrometry, GC-MS）（日本岛津公司，QP2010型）进行分析。
热解后的固体按照响应曲面模型设计出的15个试验点在气氛炉（上海卓的仪器有限公司，SA2-1-12TP型）中于空气气氛下进行脱碳处理去除表面热解炭，并使用显微镜（日本奥林巴斯公司，SZX16型）观察纤维表面形态。

1.4 Box-Behnken实验设计

响应曲面试验采用Box Behnken Design（BBD）模型[20]设计工况。热解−脱碳实验中脱碳阶段最为关键且耗时更长，以脱碳温度（x1）、保温时间（x2）和脱碳过程升温速率（x3）为自变量，回收玻璃纤维的最大荷重（W）为因变量，进行三因子三水平的实验设计，各因子水平的设定通过单因素试验确定，试验因素和水平见表2，中心点重复三次，共生成15个试验点。
表2 编码值和水平

Table 2 Coding value and level

因素 编码值和水平
−1 0 1
脱碳温度/℃ 400 500 600
保温时间/min 30 45 60
升温速率/(℃/min) 5 10 15

1.5 氧化反应动力学参数计算

采用TG-DSC热分析仪（德国耐驰仪器公司，STA 449F5型）分析热解后带炭玻璃纤维的氧化特性。实验以空气作为载气，设定温度从35 ℃升高至900 ℃，升温速率分别为5、10、15和20 ℃/min。
利用所得的数据，使用分布式活化能模型（distributed activation energy model, DAEM）进行反应动力学分析，在众多热解动力学模型中，DAEM模型被认为是最准确且全面的模型之一，适用于热解过程的深入分析。该模型能有效描述活化能随反应转化率的变化过程及变化范围，从而为反应机制的理解和工程应用提供依据。该模型假设整个过程由无限多个具有单个活化能的平行一阶反应组成[21]，由MIURA等[22]提出的DAEM的简化方程表示为：
$\ln \left( \frac{\alpha }{{{T}^{2}}} \right)=\ln \left( \frac{AR}{E} \right)+0.6075-\frac{E}{RT}$
式中：α为热解的升温速率，K/min（℃/min）；T为热力学温度，K；T = t + 273.15 K，t为摄氏温度，℃；A为指前因子，min−1；E为表观活化能，kJ/mol；R为气体常数，R = 8.314 J/(mol∙K)。
通过分析不同升温速率条件下的热重曲线，系统考察转化率随温度变化的规律。利用实验数据绘制ln(α/T2)与1/T的散点图，并针对不同升温速率条件下的数据进行阿伦尼乌斯直线拟合。通过分析直线的斜率和截距，确定该转化过程的活化能（E）和指前因子（A）。

2 结果与讨论

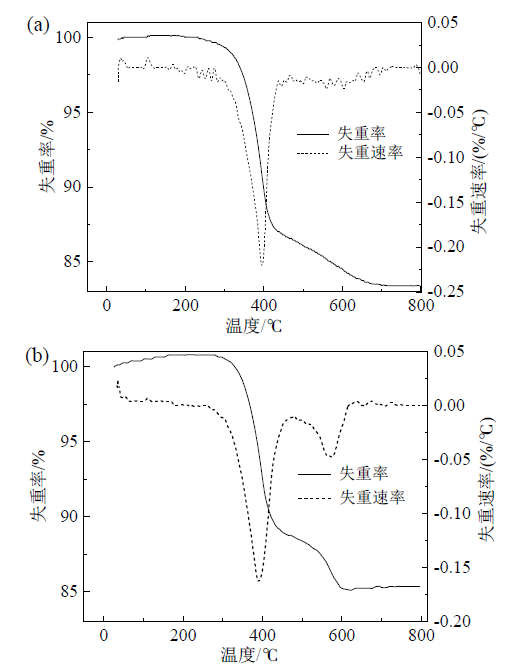
2.1 风机叶片热解规律

图2（a）为风机叶片在氮气气氛下的热重（thermogravimetry, TG）和热重微分（derivative thermogravimetry, DTG）曲线，由DTG曲线可看出只有一个主峰和一个小峰，小峰的出现是由于除环氧树脂和纤维外，风机叶片中还有部分夹芯材料，其分解温度稍高。由此风机叶片的热解大致可分为三个阶段：（1）300 ℃之前，几乎没有失重；（2）300 ~ 428 ℃风机叶片快速失重，质量损失率达到了12.09%，此阶段为快速热解阶段，398 ℃时达到了最大失重速率0.288%/℃，该过程中环氧树脂快速热解形成热稳定的炭质残留物[23]，出现大量的质量损失是由于热解过程产生大量的H2、CO、烃类气体等以及大分子芳香烃和芳香化合物被吹出造成的[23-24]；（3）428 ~ 676 ℃质量损失速率明显下降，为热解的稳定阶段，反应速率下降。根据热重结果，从节约能耗考虑，根据DTG曲线主峰结束区的温度，选择风机叶片热解温度为450 ℃，以保证热解效果并节约热解消耗的能量。
图2 风电叶片的热重和热重微分曲线：（a）N2-10 ℃/min；（b）O2-10 ℃/min

Fig. 2 TG and DTG curves of wind turbine blades: (a) N2-10 °C/min; (b) O2-10 °C/min

图2（b）为风机叶片在空气气氛下的TG和DTG曲线。相比于氮气气氛，空气气氛的DTG曲线的小峰更加明显，可能是炭氧化所致[25]。此时分四个阶段：（1）288 ℃之前，几乎无失重，说明环氧树脂在288 ℃之前是稳定的。（2）288 ~ 422 ℃风机叶片快速失重，质量损失率达到了11.46%，该阶段为快速热解阶段，391 ℃时达到了最大失重速率0.163%/℃，在空气气氛下，氧主要通过向与氧原子相连的叔碳原子引入碳−氧双键来改变环氧树脂在高温下的主链断裂，导致主链初始断裂时间提前[26]，因此在空气气氛下达到最大失重温度的时间相比氮气气氛下略有提前，该过程中风机叶片中的环氧树脂在空气气氛下快速热解。（3）422 ~ 605 ℃对应DTG曲线的第二个峰，这一阶段存在上阶段形成的热解炭的瞬态氧化[23]。（4）648 ℃之后热解反应完成，几乎没有质量损失。图2说明400 ℃之前风机叶片在空气中热解产物的微量氧化加速了热解，但是同时由于热解加快、吸热增大，说明产物被氧化所提供的放热在该温度条件下非常有限；但是420 ℃以后，由于产物中氧的存在或者供入的氧气，使得热解炭被氧化。同时图2也说明，供入氧气以后，额外被氧化的炭量有限，二者失重率相差很小，意味着氧化放热量很少，表明脱碳过程可能需要外源热量维持温度。

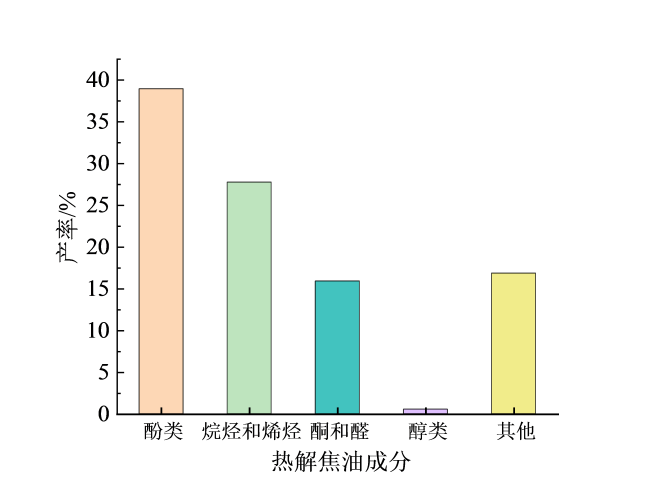
2.2 热解产物分析

风机叶片热解产物中，固体产物的质量占比为88.82%，热解油产率为3.56%，热解气产率仅为0.706%，油、气的低占比也说明了研究玻璃纤维回收的重要性。
采用气相色谱仪对气体成分进行分析，气体产物主要为H2和CO2的混合物，还有部分CO和碳氢化合物，热解产生的气体组分见表3，总热值为18.83 MJ/Nm3，该热值若用作燃料相对较低，但可用于热解的加热过程。
表3 热解气体组分

Table 3 Composition of the thermolytically produced gases

气体 体积分数/%
H2 38.44
CO2 25.71
CH4 12.98
CO 12.84
C2H4 3.86
C3H6 2.56
C3H4 1.29
C2H6 1.29
C3H8 0.64
C2H2 0.40
图3展示了热解油的组成，其主要成分为酚类、烷烃和烯烃、酮和醛、少量醇类和其他成分。酚类物质占比38.94%，为占比最高的成分，主要包括苯酚、苯酚衍生物和少量的双酚C，其中苯酚、4-异丙烯苯酚、对甲基苯酚选择率超过20%，都是被广泛应用于工业生产的重要化工原料。
图3 热解焦油各成分产率

Fig. 3 The yield of each component of pyrolysis tar

2.3 纤维表面观察

图4为原始WS4000型纤维、热解后纤维及热解 + 脱碳后纤维的显微图片，所选脱碳的纤维均为在无氧条件下以10 ℃/min升温速率处理30 min的产物。
图4 回收纤维的光学显微镜图片：（a）WS4000；（b）400 ℃；（c）500 ℃；（d）600 ℃

Fig. 4 Optical microscopy images of recovered fibers: (a) WS4000; (b) 400 °C; (c) 500 °C; (d) 600 °C

相比WS4000型纤维[图4（a）]光滑洁白的表面，热解后的纤维表面[图4（b）]附着了一层黑色的热解炭，而经过了400 ℃-30 min的脱碳处理后，纤维表面的热解炭减少，但仍有部分残留，说明400 ℃下短时间的处理无法完全去除纤维表面的热解炭。将热解温度提高到500 ℃后，黑色热解炭几乎被完全去除，只能观察到极少数热解炭附着；600 ℃时，纤维表面的热解炭实现了完全去除。
显然，高温有助于脱碳，但是高温意味着高能耗及对玻璃纤维强度的影响，因此应优化脱碳反应。

2.4 响应方程的建立

基于BBD方法、利用表2中的三因子三水平，中心点重复三次，生成了如表4所示的15组工况并给出了相应的实验结果。
表4 响应曲面试验结果

Table 4 Response surface test results

序号 脱碳温度/℃ 保温时间/min 升温速率/(℃/min) 最大荷重/N
1 400 30 10 18.21
2 400 45 5 15.82
3 400 45 15 17.92
4 400 60 10 16.60
5 500 30 5 15.11
6 500 30 15 16.20
7 500 45 10 18.80
8 500 45 10 19.20
9 500 45 10 19.33
10 500 60 5 13.23
11 500 60 15 16.76
12 600 30 10 14.99
13 600 45 5 13.16
14 600 45 15 14.66
15 600 60 10 13.67
从表4中可以看出，最大荷重的波动范围为13.16 ~19.33 N，最大荷重越大，说明回收纤维的质量越好。相同工艺参数下最大荷重也有所波动，说明多次（本研究至少8次）测量取均值的必要性。
利用表4中的数据建立响应模型，模型拟合结果见表5，p值是观察到的数据或更极端的数据在零假设成立的条件下出现的概率。在响应曲面法中，p值用于检验各个因素及其交互作用是否对响应变量有显著影响。p < 0.05时说明影响因子对响应值的影响显著，p > 0.1时则通常不考虑该因子对响应值的影响[27]。复相关系数r2是一个统计量，用于衡量一个回归模型对响应变量变异的解释能力。r2越接近1，说明拟合的模型精度越高。
表5 四种模型拟合结果

Table 5 Fitting results of four models

模型 p r2
一次模型[27] 0.068 9 0.314 8
两因子交互作用模型[28] 0.937 8 0.102 6
平方模型[20] 0.000 1 0.972 6
立方模型[29] 0.349 0 0.982 9
表5显示平方模型和立方模型的复相关系数r2都很接近1，但是立方模型的p值为0.349 0（> 0.1）；而平方模型可以获得极小的p值，因此采用平方模型。表达式为：
$W={{\beta }_{0}}\text{ +}\sum\limits_{i=1}^{k}{{{\beta }_{i}}}{{x}_{i}}+\sum\limits_{i=1}^{k}{\sum\limits_{j=1}^{k}{{{\beta }_{ij}}}}{{x}_{i}}{{x}_{j}}+\sum\limits_{i=1}^{k}{{{\beta }_{ii}}}x_{i}^{2}{{i}^{2}}+\varepsilon $
式中：W为回收纤维最大荷重的响应面函数；β0、βi、βij、βii为回归方程系数；xi为第i种参数的水平，分别有脱碳温度（x1）、保温时间（x2）和升温速率（x3）三种参数；ε为各种误差；k为工艺参数的数量，本文k = 3。
对模型的有效性进行方差分析，从而确定各个因素与响应值的关系，结果如表6所示。F值是组间方差与组内方差的比值，在F值检验中，F越大，表明模型的显著性越强，本模型的F值为56.18，p = 0.000 2，说明极显著，而失拟项的F值为2.01，p值为0.349 0，大于0.05，说明回归方程非正常误差占比小。
表6 回归模型的方差分析

Table 6 Variance analysis for regression model

来源 平方和 均方和 F p
模型 62.02 6.89 56.18 0.000 2
x1 18.21 18.21 148.47 < 0.000 1
x2 2.26 2.26 18.41 0.007 8
x3 8.45 8.45 68.86 0.000 4
x1x2 0.02 0.02 0.17 0.696 0
x1x3 0.09 0.09 0.73 0.430 8
x2x3 1.49 1.49 12.13 0.017 6
$x_{1}^{2}$ 9.32 9.32 75.98 0.000 3
$x_{2}^{2}$ 10.10 10.10 82.33 0.000 3
$x_{3}^{2}$ 16.77 16.77 136.74 < 0.000 1
残差 0.61 0.12 — —
失拟项 0.46 0.15 2.01 0.349 0
纯误差 0.15 0.08 — —
总误差 62.62 — — —
一次项的p值均小于0.05，说明脱碳温度、升温速率、保温时间均对最大荷重有显著影响，从p值的大小判断，一次项x1（温度）对最大荷重的影响最大。从交互项看，x1x2和x1x3的p值均大于0.05，说明交互影响仅需要考虑x2x3。二次项中三项的p值均小于0.05，二次项影响显著。在模型中剔除影响不显著的因子后得到拟合方程为：
$\begin{align} & W=-33.275+0.143787{{x}_{1}}\text{+ 0}\text{.544750}{{x}_{2}}\text{+} \\ & \text{1}\text{.54450}{{x}_{3}}+0.008183{{x}_{2}}{{x}_{3}}-0.000159x_{1}^{2}- \\ & 0.00735x_{2}^{2}-0.085250x_{3}^{2}\text{ } \end{align}$
式（3）中模型的复相关系数r2为0.990 2，证明模型有很高的拟合精度，与F检验的结果一致。通常，模型信噪比值大于4为宜，本模型的信噪比为21.354，信号充足，表明模型可用于风机叶片空气氧化过程的实验设计。
最大荷重的预测值与实际值的比较如图5所示，各散点均匀地分布在相关线附近，表明预测值和实际值基本符合，且各散点并未出现对相关线的较大偏移，说明模型预测的误差较小，精度较高。
图5 最大荷重的预测值与实际值的比较

Fig. 5 Comparison of the predicted and actual maximum load

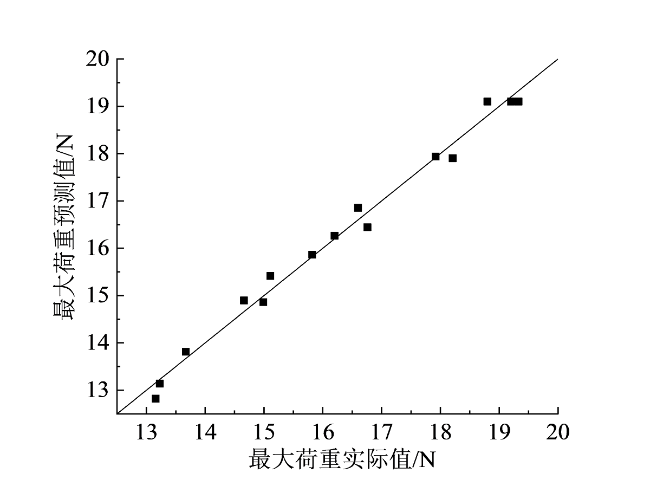
2.5 响应曲面的分析与模型的验证

图6显示了在温度为400、500和600 ℃时的3D响应曲面图。分析图6发现当保温时间和升温速率不变时，随着温度从400 ℃升高到600 ℃，最大荷重先小幅上升，然后迅速下降。这是由于较低温度时热解炭仍有附着，热解炭的附着可能降低了纤维与夹具间的摩擦力，使较低温度时测量的最大荷重较低，温度升高后热解炭去除，对拉伸性能的影响降低，最大荷重提升。而过高温的热处理会在一定程度损伤纤维，随着温度的升高，纤维的平均拉伸强度也会降低[30]。当固定脱碳温度时，最大荷重随着保温时间的延长呈现先升高后降低的趋势，改变升温速率时也出现了相似的结果，这可能与不同升温速率下和不同保温时间下热解炭的去除程度不同有关。当保温时间和升温速率同步变化时，最大荷重并不能描述为单一的升高或降低，两种因素有一定的交互作用。当升温速率较高时，相应的升温时间缩短，此时若氧化时间较短，可能会导致氧化不充分，表面热解炭去除不完全，影响了最大荷重的测量，而升温速率过低，氧化时间过长则会加剧回收纤维的缺陷程度。因此，当脱碳温度不变时，脱碳时间和升温速率这两种因素的值存在一个最合理的配置，这两个值对应曲面的最高点，即纤维的最大荷重的最大值。通过模型的计算，得出脱碳温度为452.45 ℃、保温时间为43.20 min、升温速率为11.12 ℃/min时，最大荷重能达到最高值，模型预测的最大荷重为19.61 N。而试验结果中并未包含该工况，为了对响应面模型的优化效果进行验证，需要进行二次实验。根据模型给出的最佳参数进行脱碳实验，所回收的纤维的光学显微镜照片如图7，在该优化条件下纤维表面的黑色热解炭已经可以被完全清除；对回收纤维的最大荷重进行测量，获得回收纤维的最大荷重为19.32 N，与模型预测的19.61 N相差很小，且该数值落在了模型计算出的95%置信区间下限19.20 N和95%置信区间上限20.02 N之间，证明了建立的响应曲面模型的可靠性。原始WS4000型纤维的最大荷重为37.69 N，说明回收纤维的强度达到了原纤维的51.2%，机械强度约降低了一半。
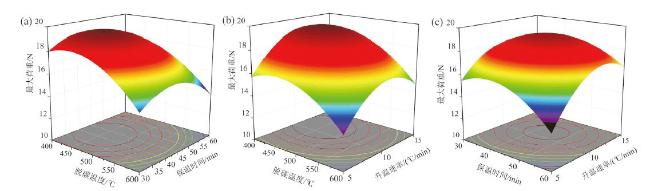
图6 不同因子对回收纤维最大荷重影响的响应曲面图：（a）脱碳温度和保温时间对最大荷重的影响；（b）脱碳温度和升温速率对最大荷重的影响；（c）保温时间和升温速率对最大荷重的影响

Fig. 6 The response surface diagram of the effects of different factors on the maximum load of recovered fibers: (a) the effect of decarburization temperature and holding time on the maximum load; (b) the effect of decarburization temperature and heating rate on the maximum load; (c) the influence of holding time and heating rate on the maximum load

图7 优化工艺参数后回收的玻璃纤维

Fig. 7 Optical microscope image of recovered fibers after optimizing parameters

2.6 氧化脱碳反应动力学分析

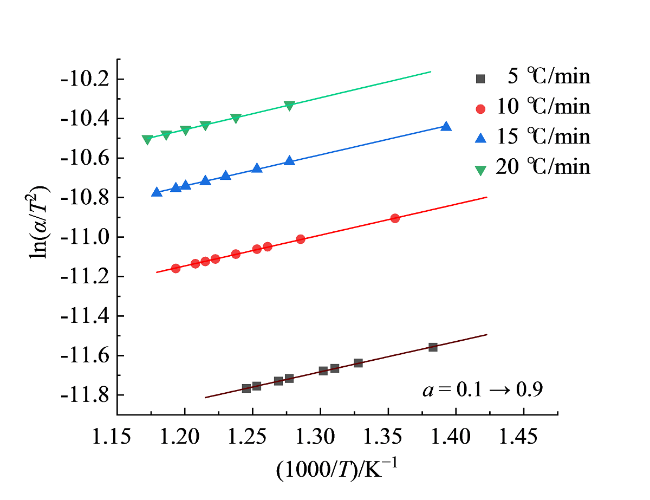
图8为DAEM法拟合的ln(α/T2) ~ 1000/T关系曲线，每种升温速率下的不同点代表不同的转化率（a）下ln(α/T2)和1000/T的对应值，对这些实验数据点进行直线拟合，并通过斜率计算得出表观活化能、指前因子和复相关系数，结果如表7所示。其中复相关系数r2越接近1，说明模型拟合效果越好，结果越精确。除转化率为0.4 ~ 0.5时复相关系数较低，其余转化率时复相关系数均较好，且随着转化率的增加，活化能呈现出先升高后降低的趋势，转化率为0.1 ~ 0.3时，活化能约为116 kJ/mol，转化率为0.5时活化能达到192 kJ/mol，随后在转化率为0.6 ~ 0.9时活化能降低，这表明玻璃纤维表面热解炭的氧化难度随着反应的进行先增大后减小。指前因子的变化趋势与活化能相近，活化能的变化与MA等[21]在N2中的结果有所不同，在惰性气氛中活化能的大小保持稳定，说明带碳纤维的氧化是一个复杂的过程，多个反应同时进行。
图8 DAEM法拟合的ln(α/T2) ~ 1000/T关系曲线

Fig. 8 Plot of ln(α/T2) versus 1000/T according to DAEM method

表7 不同转化率下的活化能和指前因子

Table 7 Activation energy and pre-exponential factor at different conversion rates

a E/(kJ/mol) A/min−1 r2
0.1 103.393 1.5 × 103 0.961
0.2 122.257 2.2 × 104 0.885
0.3 126.974 4.1 × 104 0.853
0.4 111.926 3.6 × 103 0.294
0.5 191.993 6.8 × 108 0.743
0.6 165.638 8.1 × 106 0.848
0.7 132.541 4.1 × 104 0.889
0.8 149.538 4.5 × 105 0.956
0.9 133.639 3.2 × 104 0.939
平均值 137.544 7.7 × 107 −

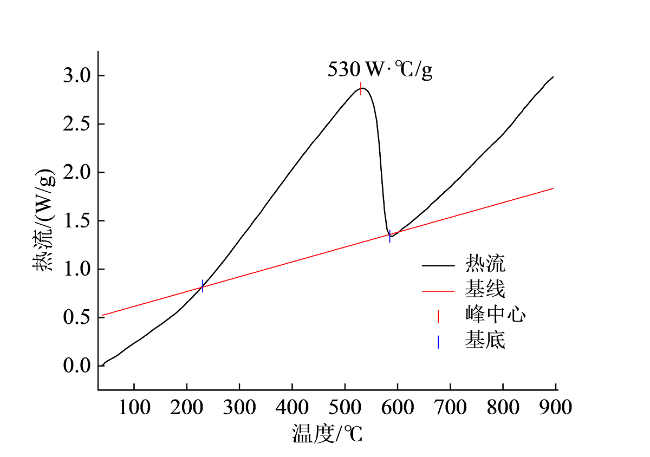
2.7 热解及脱碳能耗分析

热解能耗分析包括废风电叶片升温所需热量（Q1）、废风电叶片热解反应热（Q2）、热解气体产物燃烧释放能量（Q3）和热解焦油燃烧释放能量（Q4）。
本研究所用废风电叶片中玻璃纤维和环氧树脂质量占比分别为79%和21%，以1 kg废风电叶片为例，玻璃纤维比热约为0.9 kJ/(kg∙K)，环氧树脂比热与温度的关系为[31]：
${{c}_{p1}}=-171.2+5.47T, (T<400K)$
${{c}_{p\text{2}}}=4405.9-5.95T, (T\ge 400K)$
式中：cp1、cp2为环氧树脂的比热，kJ/(kg∙K)。因此风电叶片升温所需热量为：
$\begin{align} & {{Q}_{1}}=0.21\left( \int_{298}^{400}{{{c}_{p1}}}\text{d}T\text{+}\int_{\text{400}}^{\text{723}}{{{c}_{p2}}}\text{d}T \right)+ \\ & 0.79\times 0.9\times \left( 450-25 \right) \end{align}$
热解反应热Q2根据杨韧等[32]研究中确定为 +2 045 kJ/kg，Q3及Q4的计算根据测得的气体和焦油产物种类、比例和热值计算，计算结果见表8。
表8 风电叶片热解系统能量平衡分析

Table 8 Energy balance for waste wind blade pyrolysis system

能量需求/(kJ/kg) 可利用能量/(kJ/kg)
Q1 Q2 合计 Q3 Q4 合计
588.05 2 045.00 2 633.05 2 732.46 454.61 3 187.07
从表8中可以看出，热解能量需求小于热解系统产出可利用的能量，该热解系统可以实现能量自给，无需外部热源的热量供给。
脱碳过程中炭的氧化过程放热（Q5）如图9所示，经积分得放热量为530 W∙℃/g，单位换算后得Q5为318 kJ/kg。
图9 10 ℃/min的升温速率下热解后纤维在空气气氛中升温氧化的DSC曲线

Fig. 9 DSC curve of pyrolysis fibers loaded with pyrolysis char at a heating rate of 10 °C/min under air

玻璃纤维升温所需热量Q6为：
${{Q}_{6}}=0.9\times \left( 452.45-25 \right)=384.52\text{ kJ/kg}$
氧化过程释放热量Q5 < Q6，不足以支撑冷却后的回收纤维再次升温到脱碳温度所需热量，因此，氧化过程需要外部热源的供应。但考虑到热解过程中有较大的能量盈余，可将热解与氧化整合在同一系统。在工序必须分开时，采用更低的脱碳温度可以降低外部热源的消耗。

3 结论

系统研究了废风电叶片中增强玻璃纤维利用热解−氧化工艺回收时关键工艺参数对增强纤维的强度影响，对反应的动力学和能量平衡进行分析。获得如下结论：
（1）脱碳温度对增强纤维的力学影响最为显著，过高的脱碳温度会使回收纤维的最大荷重急剧下降。升温速率和保温时间对最大荷重也有影响，并且两者交互影响显著。
（2）通过响应曲面法优化，拟合出三个关键参数对最大荷重的预测方程。通过模型预测的最佳工艺参数为脱碳温度（x1）452.45 ℃、保温时间（x2）43.20 min、升温速率（x3）11.12 ℃/min。此时增强纤维获得的最大荷重均值为19.32 N，与模型预测的数值19.61 N基本一致，是所用的WS4000型原纤维强度的51.2%。
（3）热解−氧化脱碳回收风机叶片中的增强纤维在热解段的能耗可自平衡；氧化脱碳段仅仅炭的氧化放热尚不足升温及维持较高的脱碳温度，因此更低的脱碳温度更为节能，或者与热解耦合进行。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
雷志文. 废风机叶片热解特性及制备双酚A机理研究[D]. 武汉: 华中科技大学, 2022. DOI: 10.27157/d.cnki.ghzku.2022.004537.

[2]
陈天啸. 风力发电叶片回收技术及发展展望[J]. 玻璃纤维, 2022(6): 30-36. DOI: 10.3969/j.issn.1005-6262.2022.06.007.

[3]
ENEVOLDSEN P. A socio-technical framework for examining the consequences of deforestation: a case study of wind project development in Northern Europe[J]. Energy policy, 2018, 115: 138-147. DOI: 10.1016/j.enpol.2018.01.007.

[4]
BATH A. Global wind report 2023[R]. Bruxelles: Global Wind Energy Council, 2023.

[5]
RANI M, CHOUDHARY P, KRISHNAN V, et al. A review on recycling and reuse methods for carbon fiber/ glass fiber composites waste from wind turbine blades[J]. Composites part B: engineering, 2021, 215: 108768. DOI: 10.1016/j.compositesb.2021.108768.

[6]
张雪伟. 设计叶片时应考虑退役后的回用需求[J]. 风能, 2018(6): 31-32. DOI: 10.3969/j.issn.1674-9219.2018.06.007.

[7]
许冬梅, 张兴林, 荆涛. 废旧热固性复合材料绿色回收利用关键技术研究——以风电行业废弃风叶片为例[J]. 环境保护, 2019, 47(20): 54-56. DOI: 10.14026/j.cnki.0253-9705.2019.20.013.

[8]
蔡晓萍, 段华波, 马艺, 等. 基于生命周期分析的风机叶片环境影响评价[J]. 深圳大学学报理工版, 2023, 40(1): 40-47. DOI: 10.3724/SP.J.1249.2023.01040.

[9]
PAULSEN E B, ENEVOLDSEN P. A multidisciplinary review of recycling methods for end-of-life wind turbine blades[J]. Energies, 2021, 14(14): 4247. DOI: 10.3390/en14144247.

[10]
陈瑞哲, 程磊磊, 顾菁, 等. 纤维增强树脂复合材料化学回收技术研究进展[J]. 化工学报, 2023, 74(3): 981-994. DOI: 10.11949/0438-1157.20221489.

[11]
余丹, 孙永斌, 杨琦, 等. 风机叶片回收技术现状与展望[J]. 南方能源建设, 2023, 10(4): 113-121. DOI: 10.16516/j.gedi.issn2095-8676.2023.04.011.

[12]
马文静, 张宇彤, 杨春振, 等. 大宗风电退役风机叶片资源化回收利用技术研究进展[J]. 洁净煤技术, 2023, 29(10): 17-26. DOI: 10.13226/j.issn.1006-6772.CN23053101.

[13]
YANG Y X, BOOM R, IRION B, et al. Recycling of composite materials[J]. Chemical engineering and processing: process intensification, 2012, 51: 53-68. DOI: 10.1016/j.cep.2011.09.007.

[14]
KIM K W, LEE H M, AN J H, et al. Recycling and characterization of carbon fibers from carbon fiber reinforced epoxy matrix composites by a novel super-heated-steam method[J]. Journal of environmental management, 2017, 203: 872-879. DOI: 10.1016/j.jenvman.2017.05.015.

[15]
GIORGINI L, LEONARDI C, MAZZOCCHETTI L, et al. Pyrolysis of fiberglass/polyester composites: recovery and characterization of obtained products[J]. FME transactions, 2016, 44(4): 405-414. DOI: 10.5937/fmet1604405G.

[16]
MEYER L O, SCHULTE K, GROVE-NIELSEN E. CFRP-recycling following a pyrolysis route: process optimization and potentials[J]. Journal of composite materials, 2009, 43(9): 1121-1132. DOI: 10.1177/0021998308097737.

[17]
ELFGHI F M. A hybrid statistical approach for modeling and optimization of RON: a comparative study and combined application of response surface methodology (RSM) and artificial neural network (ANN) based on design of experiment (DOE)[J/OL]. Chemical engineering research and design, 2016, 113: 264-272. DOI: 10.1016/j.cherd.2016.05.023.

[18]
吴玉胜, 于猛, 李来时, 等. 基于响应曲面法的钾长石提钾优化工艺[J]. 沈阳工业大学学报, 2023, 45(1): 36-42. DOI: 10.7688/j.issn.1000-1646.2023.01.07.

[19]
American Society of Testing Materials (ASTM). Standard test method for tensile properties of glass fiber strands, yarns, and rovings used in reinforced plastics: ASTM D2343-17(2023)[S/OL]. [2025-01-15]. https://www.astm.org/d2343-17r23.html.

[20]
BEG S, AKHTER S. Box-Behnken designs and their applications in pharmaceutical product development[M]// BEG S. Design of Experiments for Pharmaceutical Product Development. Singapore: Springer, 2021: 77-85. DOI: 10.1007/978-981-33-4717-5_7.

[21]
MA C, SÁNCHEZ-RODRÍGUEZ D, KAMO T. A comprehensive study on the oxidative pyrolysis of epoxy resin from fiber/epoxy composites: product characteristics and kinetics[J]. Journal of hazardous materials, 2021, 412: 125329. DOI: 10.1016/j.jhazmat.2021.125329.

[22]
MIURA K, MAKI T. A simple method for estimating f(E) and k0(E) in the distributed activation energy model[J]. Energy & fuels, 1998, 12(5): 864-869. DOI: 10.1021/ef970212q.

[23]
TRANCHARD P, DUQUESNE S, SAMYN F, et al. Kinetic analysis of the thermal decomposition of a carbon fibre-reinforced epoxy resin laminate[J]. Journal of analytical and applied pyrolysis, 2017, 126: 14-21. DOI: 10.1016/j.jaap.2017.07.002.

[24]
毛俊杰, 王志, 文放, 等. 多层碳纤维/环氧树脂复合材料热解动力学[J]. 沈阳航空航天大学学报, 2022, 39(2): 21-27. DOI: 10.3969/j.issn.2095-1248.2022.02.003.

[25]
宋金梅, 刘辉, 王雷, 等. 废弃碳纤维/环氧树脂复合材料的热解特性及动力学研究[J]. 玻璃钢/复合材料, 2019(1): 47-53. DOI: 10.3969/j.issn.1003-0999.2019.01.008.

[26]
ZHANG X X, WU Y J, WEN H, et al. The influence of oxygen on thermal decomposition characteristics of epoxy resins cured by anhydride[J]. Polymer degradation and stability, 2018, 156: 125-131. DOI: 10.1016/j.polymdegradstab.2018.08.006.

[27]
FERREIRA S L C, BRUNS R E, FERREIRA H S, et al. Box-Behnken design: an alternative for the optimization of analytical methods[J]. Analytica chimica acta, 2007, 597(2): 179-186. DOI: 10.1016/j.aca.2007.07.011.

PMID

[28]
BOX G E P, WILSON K B. On the experimental attainment of optimum conditions[M]// KOTZ S, JOHNSON N L. Breakthroughs in Statistics. New York: Springer, 1992: 270-310. DOI: 10.1007/978-1-4612-4380-9_23.

[29]
GUNST R F, MYERS R H, MONTGOMERY D C. Response surface methodology: process and product optimization using designed experiments[J]. Technometrics, 1996, 38(3): 285. DOI: 10.2307/1270613.

[30]
CUNLIFFE A M, WILLIAMS P T. Characterisation of products from the recycling of glass fibre reinforced polyester waste by pyrolysis[J]. Fuel, 2003, 82(18): 2223-2230. DOI: 10.1016/S0016-2361(03)00129-7.

[31]
DING Y, CHEN Z W, TANG C Y, et al. Development of a pyrolysis reaction model for epoxy based flame retardant composites: relationship between pyrolysis behavior and material composition[J]. Chemical engineering journal, 2024, 495: 153628. DOI: 10.1016/j.cej.2024.153628.

[32]
杨韧, 林德智, 杨泓钰, 等. 六氟化硫—环氧树脂的热分解研究[J]. 高压电器, 2024, 60(4): 139-145. DOI: 10.13296/j.1001-1609.hva.2024.04.017.

Options
文章导航

/

〈 〉

主管单位：中国科学院
主办单位：中国科学院广州能源研究所
ISSN 2095-560X　
CN 44-1698/TK
地址：广州市天河区五山能源路2号广州能源所《新能源进展》编辑部　
邮编：510640　
电话：+86-20-87057066　
E-mail：xnyjz@ms.giec.ac.cn
微信公众号
粤ICP备11089167号-2　 版权所有 © 《新能源进展》编辑部