0 引言
天然气水合物具有储量大和能量密度高的优势，是一种极具开发前景的战略新兴能源[1-2]。天然气水合物储层的准确识别、精细定量评价、动态实时监测是其开发和利用的前提[3⇓-5]，地震勘探和声波测井成为常用且有效的地球物理技术。天然气水合物的存在会改变沉积物的声波速度、声波能量衰减、密度、体积模量、剪切模量等基本物理特性[6⇓⇓⇓-10]。然而，这些物理特性的变化不仅与水合物饱和度和微观赋存模式有关，也与沉积物颗粒排列方式和颗粒形状密切相关。天然气水合物储层沉积环境条件差异、水合物开采过程中地层有效压力变化，均会导致水合物饱和度、微观分布模式、骨架颗粒排列方式、颗粒/孔隙形状等的不同，进而影响含水合物沉积物声学特性的变化。
针对骨架颗粒排列方式和颗粒形状对沉积物声学特性影响的问题，LEURER[11]采用模拟实验的方法研究了细粒松散海洋沉积物的有效压力变化与骨架结构、孔隙度、声速和声衰减之间的关系。CHO等[12]在获得石英砂颗粒球度、圆度、平滑度等形状量化参数的基础上，探讨了颗粒形状对天然砂密度、刚度和强度的影响。卢博等[13]探讨了沉积物颗粒排列方式、颗粒形状、粒径对孔隙度、声速和声衰减的影响。刘强等[14]基于海底沉积物声衰减实验测量结果讨论了沉积物颗粒因素（颗粒尺寸和形状、颗粒间的相互接触关系等）与声衰减的关系。在开展单轴压缩实验的基础上，周志刚等[15]探讨了通过施加不同压力引起的颗粒样品轴向形变增加对颗粒体系内部接触结构及声波传播特性的影响。LIU等[16]应用激光扫描技术测量了颗粒的形状并量化为形状参数，研究了颗粒形状参数对刚度参数和剪切波速度的影响。以上研究工作提供了特定条件下的实验测试数据，提高了对沉积物微观结构参数影响声学特性参数的认识。然而，在实验中难以制作具有单一颗粒排列方式和颗粒形状的测试样本，因此无法准确地获取不同的骨架颗粒排列方式和形状条件下的沉积物声学特性参数，从而不能严格地探讨颗粒排列方式和形状对沉积物声学特性的影响机理。数字岩石物理技术为开展上述工作提供了有效的技术手段。
针对水合物饱和度和赋存模式对沉积物声学特性影响的问题，研究人员开展了理论模拟或数值模拟工作。SAVA等[17]针对高度非固结沉积物中水合物微观分布的四种模式分别建立了岩石物理模型，通过模拟计算研究了沉积物弹性性质对水合物分布几何结构的依赖性。YANG等[18]模拟了地震波在海底天然气水合物沉积层中的传播特性并获取了纵波和横波速度，研究了水合物微观分布模式、水合物饱和度和游离气饱和度对沉积物弹性性质的影响。卜庆涛等[19]分别构建了实验和储层尺度的近似地质模型，结合等效介质理论得到不同水合物饱和度和微观分布模式条件下沉积物的弹性参数，基于有限差分法求解双相介质二维波动方程，获得了不同水合物饱和度条件下模型中的波场和波速。徐源等[20]在建立有限元数值模型的基础上探讨了微观赋存模式和水合物饱和度对多孔介质声速和声衰减的影响规律。目前，针对含水合物沉积物中骨架颗粒排列方式和形状对沉积物声学特性影响规律的研究鲜有报道。
本文以前期电−力−声多物理场耦合建模方法为基础[20]，考虑有效应力引起的骨架颗粒排列方式和骨架颗粒形状的变化，建立含水合物沉积物有限元数值模型，探讨典型水合物分布模式下骨架颗粒排列方式和颗粒形状对沉积物声速和声衰减特性的影响规律和机理，以期为天然气水合物储层地震勘探和声波测井数据的解释提供理论支撑。
1 含水合物多孔介质建模
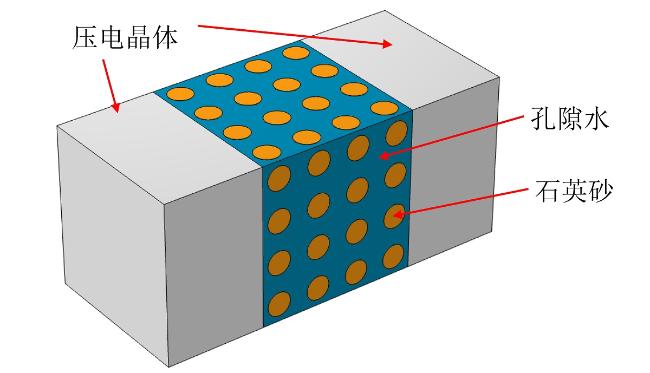
1.1 建模方法
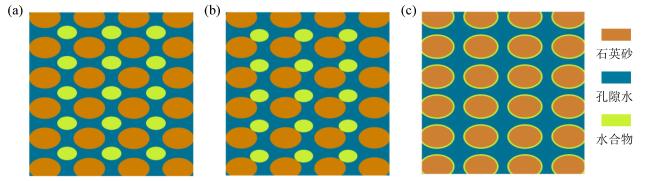
1.2 菱形排列模型
等径圆球颗粒是一个经典的理论模型，沉积物声学特性受到孔隙度的影响，而等径圆球颗粒堆积起来的多孔介质的孔隙度与颗粒粒径无关，只与颗粒的排列方式有关。BEAR[21]研究了圆球颗粒在不同堆积方式下的最大孔隙度。最松散的排列方式为立方排列，最大孔隙度为47.64%；最紧密的排列方式为菱形排列（每个圆球与相邻的12个圆球相切），最大孔隙度为25.96%。
本文构建的菱形排列模型包含147个尺寸相同的球形石英砂颗粒，半径r为0.21 mm，石英砂颗粒之间以面接触的方式排列，接触面积为单个石英砂圆球颗粒总外表面积的1.1%，多孔介质几何结构的孔隙体积约为1.07 mm3，孔隙度φ为25%。对于实际的沉积物，有效压力的变化会引起骨架结构和孔隙结构的变化，如骨架颗粒/孔隙的变形、骨架颗粒排列方式的转变、孔隙度的变化等，进而引起沉积物声学特性的变化。
悬浮模式条件下，当水合物与石英砂相切时水合物饱和度为0.24，因此在数值模型中设定水合物饱和度范围为0.02 ~ 0.22。在悬浮与接触模式条件下，上述水合物饱和度范围对应的水合物颗粒半径R1的范围为18.78 ~ 41.71 μm；胶结模式条件下水合物层的厚度范围为0.57 ~ 5.67 μm。
1.3 椭球颗粒模型
椭球颗粒模型由96个石英砂颗粒和45个水合物颗粒构成，石英砂颗粒采用立方排列方式，模型中孔隙体积约为1.7 mm3，孔隙度为41%。构建三种水合物赋存模式条件下的椭球颗粒模型，石英砂颗粒之间采用面接触方式，接触面积为单个椭球状石英砂颗粒外表面积的6.2%。
设置声速在沉积物中从左往右传播[以图3（a）为例]，为了得到不同的水合物饱和度，对于悬浮和接触模式，保持水合物颗粒的位置固定，改变椭球水合物颗粒的短轴和长轴长度，固定纵横比为0.68。对于胶结模式，改变石英砂颗粒表面水合物层的厚度。在悬浮模式条件下，当水合物与石英砂相切时水合物饱和度为0.30，为了与上文菱形排列模型进行对比，选取相同的饱和度范围，即0.02 ~ 0.22。在悬浮与接触模式条件下，上述水合物饱和度范围对应的水合物椭球颗粒的长轴和短轴范围分别为64.84 ~ 152.44 μm和44.21 ~ 103.94 μm，胶结模式下水合物层厚度范围为1.02 ~ 11.65 μm。
2 颗粒排列方式对含水合物多孔介质声学特性的影响
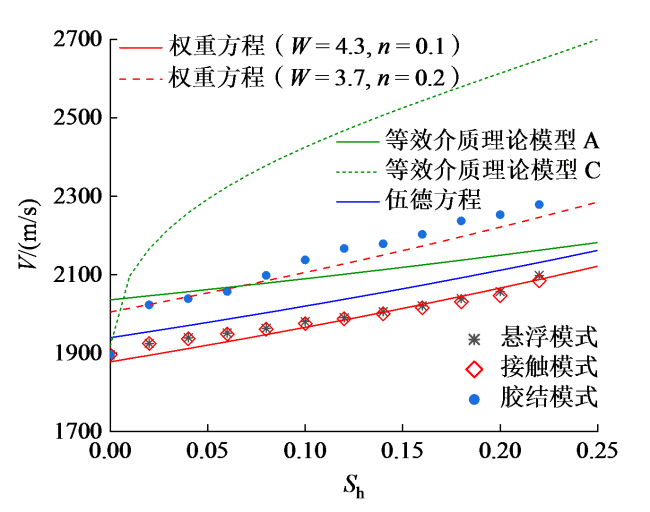
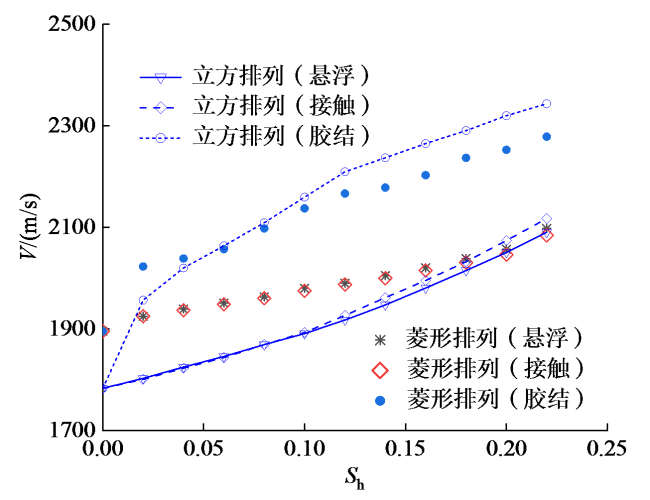
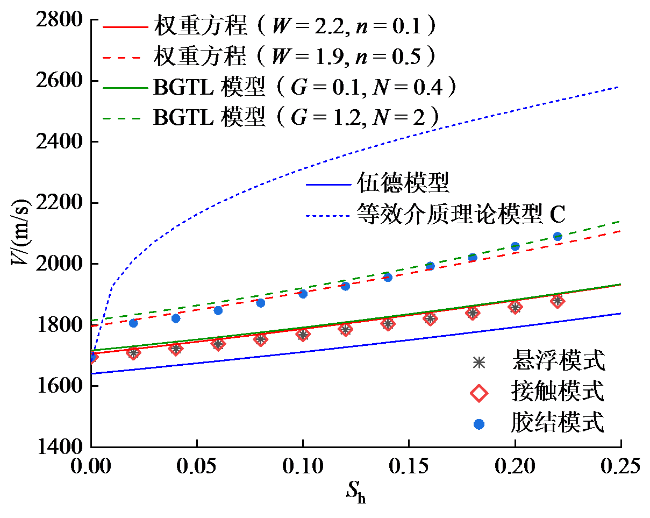
2.1 颗粒排列方式对声速的影响
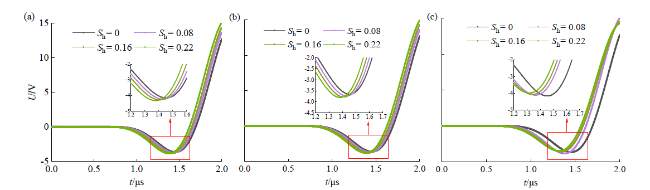
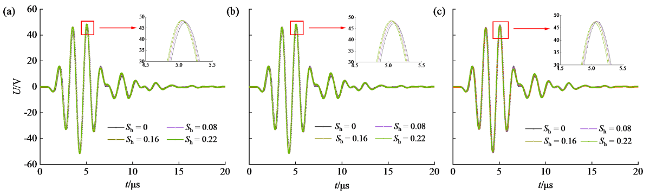
图4 菱形排列模型接收的声波信号（时间长度为2 μs）：（a）悬浮模式；（b）接触模式；（c）胶结模式Fig. 4 Received acoustic waves of diamond-arrangement models (time period of 2 μs): (a) suspending mode; (b) contact mode; (c) cementation mode |
$V=\sqrt{\frac{k+4\mu /3}{\rho }}$
式中：k、μ、ρ分别为沉积物的体积模量、剪切模量和密度。
对于菱形排列模型的悬浮和接触模式下的声速变化曲线，在所研究的水合物饱和度区间内，等效介质理论模型A对多孔介质声速的预测值偏高，权重方程（W = 4.3，n = 0.1）和伍德方程预测值与仿真结果较为接近。当水合物饱和度为0时，多孔介质的声速为1 895.3 m/s，与文献[28]所报道的经验模型结果一致；当水合物饱和度为0.22时，悬浮和接触模式下多孔介质的声速分别达到2 097.8 m/s和2 084.1 m/s。对于胶结模式，声速数值模拟结果高于伍德方程和等效介质理论模型A，低于等效介质理论模型C的计算结果，在0.02 ~ 0.22饱和度范围内，权重方程（W = 3.7，n = 0.2）与数值模拟结果高度一致；水合物多孔介质中水合物饱和度由0.2升至0.22时，声速随水合物饱和度的增长速率趋于稳定，饱和度为0.22时声速达到2 278.6 m/s。
分析图6可知，对于悬浮和接触模式，在水合物饱和度为0 ~ 0.18时，菱形排列模型的声速高于立方排列模型，随着水合物饱和度的升高，两者差异逐渐减小，在0.20 ~ 0.22的水合物饱和度区间内，两种排列方式条件下的声速差异不显著；对于胶结模式，在0.02 ~ 0.06较低饱和度范围内，骨架颗粒菱形排列模型的声速高于立方排列模型，在0.08 ~ 0.22较高饱和度范围内，该模型的声速低于立方排列模型。
在水合物饱和度较低时，沉积物整体弹性模量受到石英砂颗粒影响较大，与沉积物颗粒立方排列时相比，骨架颗粒菱形排列时的沉积物孔隙度相对较小，具有高弹性模量的石英砂颗粒体积占比相对较大，则菱形排列模型的声速相对更高。当水合物饱和度分别为0.02和0.20时，水合物在菱形排列模型和立方排列模型中的体积占比差异分别为0.34%和3.40%，水合物在立方排列中的体积占比相对更高。随着水合物饱和度的升高，由于水合物的声速高于水的声速，沉积物的声速随之升高，然而两类模型中水合物的体积占比差异随之逐渐增大，导致两类模型声速增大的速率有所差异，由于水合物在立方排列模型中的体积占比相对更高，则菱形排列模型的声速增长速率低于立方排列模型，最终导致悬浮和接触模式下两类排列方式模型的声速逐渐接近，而胶结模式下菱形排列模型的声速相对更低。
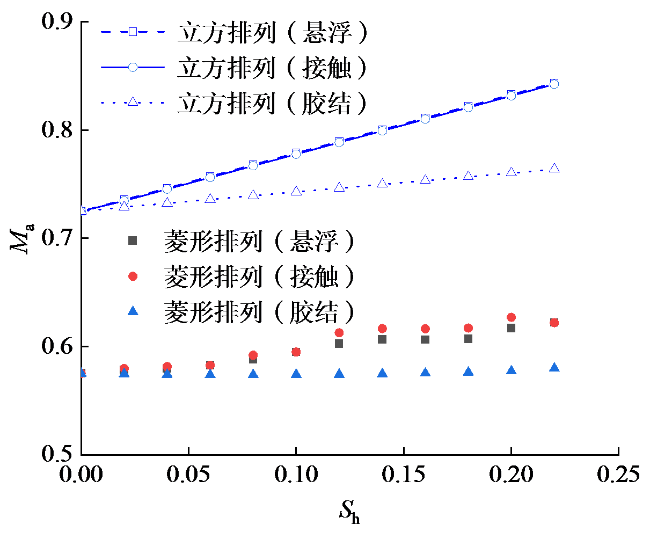
2.2 颗粒排列方式对声衰减的影响
通过对数值模型进行求解，得到含悬浮模式、接触模式和胶结模式水合物多孔介质接收端的声波信号，如图7所示。在研究声波信号的衰减特性时，将接收端电压信号的振幅Um（以电压波形的最大值来表示）作为考察指标，激励端电压信号的振幅为Um0。基于信号振幅的降低定义用于量化声波能量衰减的参数Ma，Ma由式（2）计算得到。
${{M}_{\text{a}}}=\frac{{{U}_{\text{m}0}}-{{U}_{m}}}{{{U}_{\text{m}0}}}$
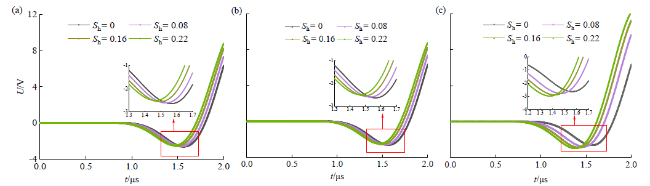
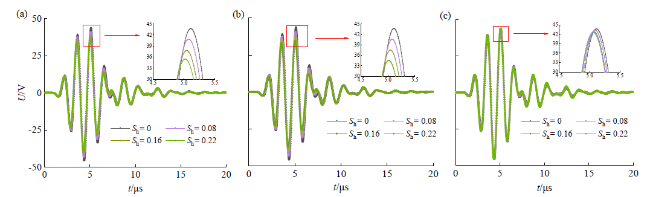
图7 菱形排列模型接收的声波信号（时间长度为20 μs）：（a）悬浮模式；（b）接触模式；（c）胶结模式Fig. 7 Received acoustic waves of diamond-arrangement models (time period of 20 μs): (a) suspending mode; (b) contact mode; (c) cementation mode |
分析图7和图8可知，三种水合物赋存模式下，菱形排列模型的接收信号幅值随着水合物饱和度的升高而减小，可见Ma随着水合物饱和度的升高而增大；在水合物饱和度相同的条件下，悬浮和接触模式条件下的声衰减差异较小，胶结模式条件下的声衰减显著低于悬浮和接触模式。水合物胶结模式下沉积物组分间的分界面与悬浮和接触模式下有所差异。在悬浮和接触模式条件下，石英砂和水合物均与孔隙水直接接触，两类固/液界面的声阻抗差别较大，在界面处声波能量衰减大；在胶结模式条件下，上述固/液界面转换成了石英砂与水合物界面（固/固）、水合物与孔隙水（固/液）界面，由于水合物与石英砂之间的声阻抗差异小于孔隙水与石英砂之间声阻抗差异，因此声波传播过程中能量衰减相对较少，即胶结模式下声波在传播过程中的衰减显著低于悬浮和接触模式。
3 骨架颗粒形状对含水合物多孔介质声学特性的影响
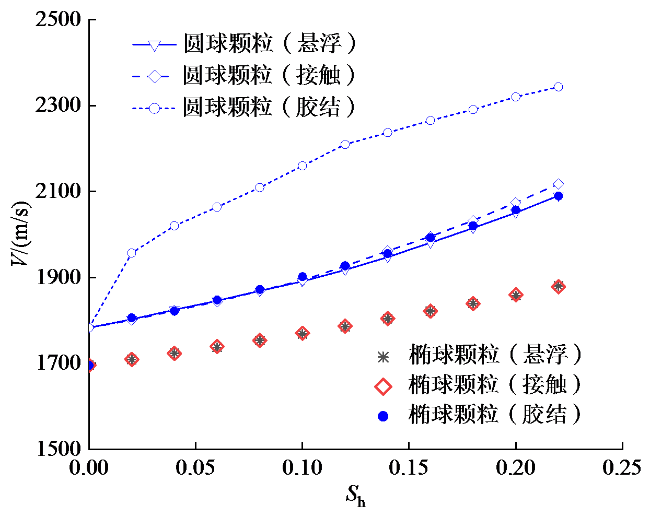
3.1 颗粒形状对声速的影响
图9 椭球颗粒模型接收的声波信号（时间长度为2 μs）：（a）悬浮模式；（b）接触模式；（c）胶结模式Fig. 9 Received acoustic waves of ellipsoidal-particle models (time period of 2 μs): (a) suspending mode; (b) contact mode; (c) cementation mode |
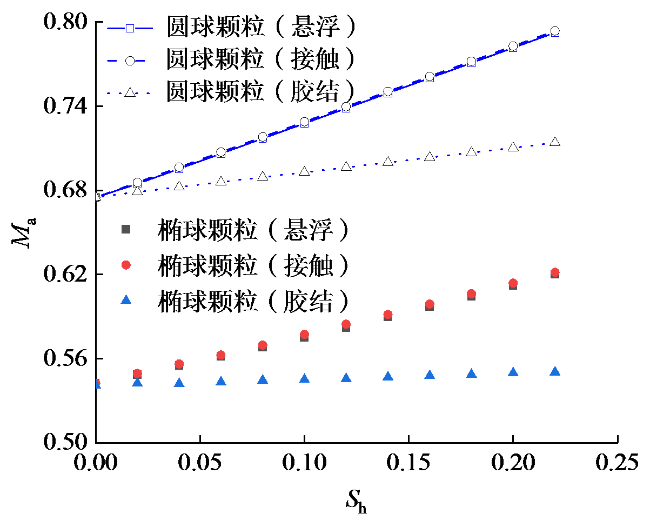
3.2 颗粒形状对声衰减的影响
图12 椭球颗粒模型接收的声波信号（时间长度为20 μs）：（a）悬浮模式；（b）接触模式；（c）胶结模式Fig. 12 Received acoustic waves of ellipsoidal-particle models (time period of 20 μs): (a) suspending mode; (b) contact mode; (c) cementation mode |
分析图12和图13可知，三种水合物赋存模式下，椭球颗粒模型中接收信号的幅值随着水合物饱和度的升高而减小，可计算得到Ma随着水合物饱和度的升高而增大。在水合物饱和度相同的条件下，悬浮和接触模式条件下的声衰减差异较小，胶结模式条件下的声衰减显著低于悬浮和接触模式。水合物胶结模式下沉积物组分间的分界面与悬浮和接触模式下有所差异。在悬浮和接触模式条件下，石英砂和水合物均与孔隙水直接接触，两类固/液界面的声阻抗差别较大，在界面处声波能量衰减大；在胶结模式条件下，以上固/液界面转换成了石英砂与水合物界面（固/固）、水合物与孔隙水（固/液）界面，由于水合物与石英砂之间的声阻抗差异小于孔隙水与石英砂之间声阻抗差异，因此声波传播过程中能量衰减相对较少。
4 讨论
以上对比了骨架颗粒菱形排列和立方排列的多孔介质模型、骨架颗粒为椭球和圆球的模型，探讨了骨架颗粒排列方式、骨架颗粒形状对含水合物沉积物声速和声衰减参数的影响，这对于深入认识含水合物沉积物的声学特性及其变化规律提供了基础。但是实际天然气水合物储层的沉积物包含复杂多样的颗粒排列方式和颗粒形状，因此还需探讨具有多种排列方式和多种颗粒形状条件下的含水合物沉积物的声学特性。
天然气水合物在地层中的赋存类型可分为孔隙填充型和裂隙填充型[35-36]。孔隙型水合物替代孔隙中的流体，水合物成为孔隙流体或固体骨架的一部分，可进一步细分为悬浮、接触、胶结等微观赋存模式；裂隙型水合物通过驱替或排挤颗粒来占据颗粒空间，可形成脉状、层状、透镜状等微观模式[37-38]。在我国珠江口盆地东部海域、印度Krishna-Godavari盆地、美国墨西哥湾、韩国Ulleung盆地等均发现了裂隙型水合物[39⇓⇓-42]。本文针对含孔隙型水合物沉积物的声学特性进行了探讨，将来还需建立含裂隙型水合物沉积物的电−力−声多物理场耦合数值模型，深入研究裂隙性质（角度、宽度、密度等）、颗粒排列与形状、水合物饱和度和赋存模式等因素对声学特性的影响规律和机理。
5 结论
基于电−力−声多物理场耦合建模方法建立了不同骨架颗粒排列方式和不同颗粒形状条件下的含水合物沉积物有限元数值模型，探讨了不同水合物分布模式和饱和度条件下骨架颗粒排列方式和形状对沉积物声速和声衰减特性的影响规律和机理。主要结论如下：
（1）水合物饱和度较低时，骨架颗粒菱形排列模型中石英砂颗粒体积占比相对立方排列模型中较大，菱形排列模型的声速相对较高；随着水合物饱和度的升高，两类模型中水合物体积占比差异随之增大，水合物在立方排列模型中的体积占比相对较高，菱形排列模型的声速增长速率低于立方排列模型；菱形排列模型的孔隙度小于立方排列模型，声波传播过程中能量耗散相对较低，菱形排列模型的声衰减低于立方排列模型。
（2）与圆球颗粒模型相比，椭球颗粒模型包含纵横比小且数量多的孔隙，导致椭球颗粒模型体积模量较小，在水合物微观分布模式和饱和度相同的条件下，椭球颗粒模型的声速低于圆球颗粒模型；与圆球颗粒模型相比，椭球颗粒模型孔隙的数量较多、尺寸较小，导致椭球颗粒模型中的波能损耗较少，即声衰减较低。
