欢迎访问《新能源进展》官方网站！今天是

新能源进展 >

2025 , Vol. 13 >Issue 2: 182 - 190

DOI: https://doi.org/10.3969/j.issn.2095-560X.2025.02.008

考虑余热利用的干式变压器温度分布

  • 张靖 1, 2 ,
  • 王静 3 ,
  • 赵宇明 3 ,
  • 陈炯聪 , 1, 2, † ,
  • 廖卓颖 1, 2 ,
  • 舒杰 , 1, 2, †
展开
  • 1 中国科学院广州能源研究所，广州 510640
  • 2 中国科学技术大学 能源科学与技术学院，广州 510640
  • 3 深圳供电局有限公司，广东 深圳 518000
†陈炯聪，E-mail：；
舒 杰，E-mail：

张 靖（1996-），男，博士研究生，主要从事新型电力系统的优化运行研究。

陈炯聪（1979-），男，博士，正高级工程师，主要从事新型电力系统、新能源技术研究。

舒 杰（1969-），男，博士，研究员，博士生导师，主要从事分布式可再生能源发电微电网技术、多能互补综合系统研究规划与优化控制、新能源发电电力变换与控制等研究。

收稿日期: 2024-02-27

  修回日期: 2024-03-18

  网络出版日期: 2025-04-30

基金资助

南方电网公司科技项目(090000KK52220020)

收起

Temperature Distribution of Dry-Type Transformer Considering Waste Heat Utilization

  • Jing ZHANG 1, 2 ,
  • Jing WANG 3 ,
  • Yuming ZHAO 3 ,
  • Jiongcong CHEN , 1, 2, † ,
  • Zhuoying LIAO 1, 2 ,
  • Jie SHU , 1, 2, †
Expand
  • 1 Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China
  • 2 School of Energy Science and Engineering, University of Science and Technology of China, Guangzhou 510640, China
  • 3 Shenzhen Power Supply Co. Ltd., Shenzhen 518000, Guangdong, China

Received date: 2024-02-27

  Revised date: 2024-03-18

  Online published: 2025-04-30

Fold

摘要

电力变压器在运行过程中会产生大量的余热。若对这部分余热进行回收利用，将有助电力系统低碳化运行目标的实现。为了探究变压器余热利用的可行性，建立了干式变压器模型，并对其运行温度分布进行仿真分析。首先，分别讨论分析了散热风机风速、环境温度和负载率对干式变压器温度分布的影响。随后，设计正交试验，基于温度分布的仿真数据，对神经网络进行训练，得到计算干式变压器温度分布的通用数学模型。最后，在案例分析中对两个余热利用相关区域进行仿真测试，所采用的贝叶斯-GRU模型的平均绝对百分比误差（MAPE）分别为2.24%和2.73%，决定系数R2分别为0.99和0.97，相较于单一的神经网络模型实现了大幅度的计算精度提升，体现出了较好的准确性和泛用性。该研究可以为变压器余热利用工程应用提供理论依据。

关键词： 干式变压器; 余热利用; 温度分布; 正交试验; 贝叶斯-GRU

本文引用格式

张靖 , 王静 , 赵宇明 , 陈炯聪 , 廖卓颖 , 舒杰 . 考虑余热利用的干式变压器温度分布[J]. 新能源进展, 2025 , 13(2) : 182 -190 . DOI: 10.3969/j.issn.2095-560X.2025.02.008

Abstract

Power transformers generate significant waste heat during operation. If this part of the waste heat can be recovered and utilized, it will effectively help the realization of the low-carbon operation goal of the power system. A dry-type transformer model is established to explore the feasibility of waste heat utilization of the transformer, and its operating temperature distribution is simulated. First, the influences of wind speed of the cooling fan, ambient temperature, and load rate on temperature distribution of dry-type transformers are discussed and analyzed, respectively. Furthermore, the orthogonal experiment is designed to train the neural network based on the simulation data of the temperature distribution, and a general mathematical model for calculating the temperature distribution of the dry-type transformer is obtained. Last, in the case study, simulation tests are carried out on the two positions related to waste heat utilization. The Bayes-GRU model achieves mean absolute percentage error (MAPE) values of 2.24% and 2.73%, with corresponding R2 scores of 0.99 and 0.97, demonstrating significantly enhanced calculation accuracy compared to single neural network models and reflecting superior accuracy and universality. This research can provide the theoretical basis for the engineering application of transformer waste heat utilization.

Key words： dry-type transformer; waste heat utilization; temperature distribution; orthogonal experiment; Bayes-GRU

0 引言

气候变化和能源问题是当前突出的全球性挑战。作为世界工厂和用能大国，中国的低碳结构性变革要求紧迫。在此背景下，中国政府提出了“碳达峰、碳中和”的重大战略目标[1-2]。建设新型电力系统是实现“双碳”目标的重要途径[3-5]。
降低系统损耗、减少碳排放是建设新型电力系统的关键[6-7]，对“双碳”目标的推进意义重大。据统计，2021年我国输配电损耗为3 256亿千瓦时，同时，变压器损耗约占输配电电力损耗的40%[8]。按此数据计算，仅2021年，我国电力系统中变压器损耗就高达1 302亿千瓦时，约占当年发电总量的1.5%。电力系统变压器的损耗体现为大量的余热，这部分热量不仅会造成变压器温度过高，提高发生故障的风险，还会造成大量的能量浪费。若能对这部分余热进行回收利用，将有助电力系统低碳化运行目标的实现。
目前，国内外关于变压器余热利用已有一些研究案例。例如，文献[9]将变压器的余热利用途径划分为直接利用和间接利用。其中，间接利用指将散热器内的换热媒质借助热交换器换热，再用其加热后的水供应热水、采暖和空调等，在理论上具有较好的可行性。文献[10-13]同样论述了变压器余热在采暖、制冷中的应用前景，但这些研究只局限于应用场景讨论。文献[14-17]提供了一定的算例分析结果，但并未对变压器余热的分布情况进行详细的讨论。此外，变压器余热发电也受到一些研究者的关注[18-19]，但其发电量小、效率低下的问题难以得到解决，因此不是主流研究方向。
针对变压器余热利用，现有的研究多局限于余热利用的可行性论证和经济性分析，并没有对余热的空间分布进行详细的讨论。因此，为了实现精准高效的余热利用，需要得到变压器运行时的温度分布。在这一领域，已有部分相关研究。文献[20]研究了环氧树脂材料的导热系数和绕组绝缘层厚度对绕组热点温度的影响，结果表明高压绕组的绝缘厚度减小可显著降低高压绕组的热点温度。文献[21]建立了典型干式变压器三维磁热耦合计算模型，通过数值分析得到了绕组损耗及热点温升沿圆周方向和高度方向的分布规律。文献[22]对不同冷却方式下不同负载时的绕组温度场及热点温度进行了计算与分析。然而，这类研究或为单一的数学计算，或关注变压器的结构设计，没有挖掘变压器温度分布对工程应用的实际意义。为了实现变压器余热的有效利用，有必要进行更深入的研究。
广泛分布于城乡配电网中的变压器多为干式变压器，为了实现对这类变压器的余热利用，本文将对其运行时的温度分布进行计算和分析。基于上述讨论，建立干式变压器模型，并从以下角度展开研究：一方面，分析讨论不同因素对干式变压器温度分布的影响，对其不同运行工况的温度分布进行仿真计算；另一方面，设计正交试验，基于温度分布的仿真数据，对神经网络进行训练，得到计算干式变压器温度分布的通用数学模型。本研究可为变压器余热利用实践的开展提供理论依据。

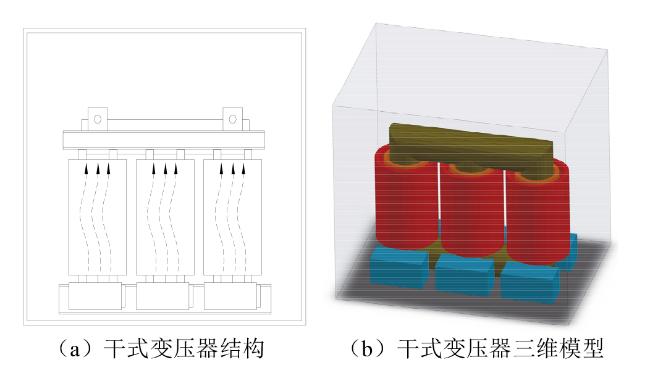
1 干式变压器模型构建

基于某近零碳建筑项目现场实际情况，以干式变压器为研究对象，建立模型来计算其温度分布。考虑到由于变压器内部结构较为复杂，过多地考虑细节会导致建模和计算难度增加，因此可以忽略对散热过程影响较小的零部件。
图1（a）为干式变压器结构示意图，其主体部分主要包括铁芯、绕组以及安装在绕组下方的散热风机。在变压器运行时，散热风机通过向上送风来调节变压器柜体内的温度。图1（b）为在SolidWorks软件中建立的干式变压器简化模型，包含变压器铁芯、三相高/低压绕组以及安装在绕组下方的六个散热风机。此外，在绕组外侧设置1 mm厚的绝缘包封层。
图1 干式变压器结构及其三维建模

Fig.1 Structure and 3D modeling of dry-type transformer

仿真分析涉及的变压器物性参数见表1。干式变压器主要铭牌技术参数见表2。
表1 干式变压器部件物性参数

Table 1 Physical parameters of dry-type transformer components

部件 材料 密度/(kg/m3) 比热容/[J/(kg⋅K)] 导热系数/[W/(m⋅K)] 电导率/(S/m) 相对磁导率
铁芯 硅钢 7 650 460 18.90 — B-H曲线
高/低压绕组 铜 8 960 385 400.00 5.998 × 107 —
风机 钢 7 850 475 44.50 — —
绕组绝缘包封 环氧树脂 1 255 1 680 0.14 — —
表2 干式变压器铭牌技术参数

Table 2 Technical parameters of dry-type transformer nameplate

参数 条件 参数 条件
型号 SCB11-800 额定容量 800 kVA
额定电压 10/0.4 kV 额定电流 46.2/1 154.7 A
空载损耗 1 274 W 负载损耗 7 146 W
绝缘等级 F 相数 3

2 干式变压器余热利用数学建模

2.1 干式变压器损耗的简化计算

变压器的损耗包括空载损耗和负载损耗两部分。其中，空载损耗主要由铁芯材料的磁滞损耗和涡流损耗组成；负载损耗主要包括直流电阻损耗和涡流损耗。为了简化运算，将变压器视为一个热源，仅考虑其体损耗，不考虑损耗的具体分布情况。
采用斯泰因梅茨（Steinmetz）方程来估算干式变压器的空载损耗：
$P_{0}=k_{\mathrm{h}} \times f^{a} \times B_{\max }^{b}$
式中：kh是与铁芯材料属性相关的系数，其值等于铁芯材料的标称损耗；a、b均为斯泰因梅茨经验系数；f为频率，Hz；Bmax为峰值磁感应强度值，T。
直流电阻损耗指电流流经变压器绕组引线在其直流电阻中引起的损耗，其表达式为：
$P_{\mathrm{DC}}=3 I_{1 \mathrm{~N}}^{2} R_{1}+3 I_{2 \mathrm{~N}}^{2} R_{2}$
式中：I1N、I2N分别为变压器一次侧、二次侧绕组额定电流，A；R1、R2分别为变压器一次侧和二次侧绕组的电阻，Ω。
此外，在中小型的配电变压器中，包含绕组涡流损耗、环流损耗等在内的附加铜损仅约占直流电阻损耗的1% ~ 5%[23]，此处将其忽略不计，并认为：
$P_{\mathrm{L}} \approx P_{\mathrm{DC}}$
式中：PL为负载损耗，W。

2.2 干式变压器的热传导原理

基于有限元分析对干式变压器运行时的传热过程进行分析。稳态时，对于铁芯、绕组等固体区域，干式变压器三维热传导控制方程为：
$\lambda\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right)=-Q$
式中：λ为材料的导热系数，W/(m⋅K)；T为求解域热源截面的热力学温度，K；Q为求解域的热流密度，W/m2。
针对空气域，采用如下的能量守恒方程来描述传热过程：
$\left\{\begin{array}{c}\rho C_{p} \frac{\partial T}{\partial t}+\rho C_{p} u \nabla T+\nabla \boldsymbol{q}=Q \\\boldsymbol{q}=-\lambda \nabla T\end{array}\right.$
式中：ρ为气体密度，kg/m3；Cp为气体的恒压比热容，J/(kg⋅K)；u为求解域气体流速，m/s；q为传导热通量矢量，J/s；$ \nabla$为哈密顿算子。
稳态条件下，$ \frac{\partial T}{\partial t}=0$，式（5）可进一步改写为：
$\rho C_{p} u \nabla T=\nabla \cdot(\lambda \nabla T)+Q$

2.3 干式变压器余热利用原理

针对干式变压器的余热有两种利用方案：其一是直接在变压器柜体内取热，该方案优先考虑变压器主体部分外围区域，即高压绕组外侧部分，这部分相对容易接触，便于取热；其二是在有安全绝缘要求，不能在柜体内部安装余热回收设备的情况下，可以考虑使用热泵或热交换器来捕获外壳附近的余热，这类情况下优先考虑柜体散热口处的余热[17]。
因此，针对余热利用，主要关注干式变压器高压绕组外侧平均温度和散热口平均温度。

3 基于正交试验的温度数值计算模型

为了得到通用的干式变压器温度分布数值计算模型，在温度分布仿真的基础上，设计三因素五水平正交表；基于温度分布仿真的数据，进一步对神经网络进行训练，得到计算干式变压器温度分布的通用数学模型。

3.1 正交试验

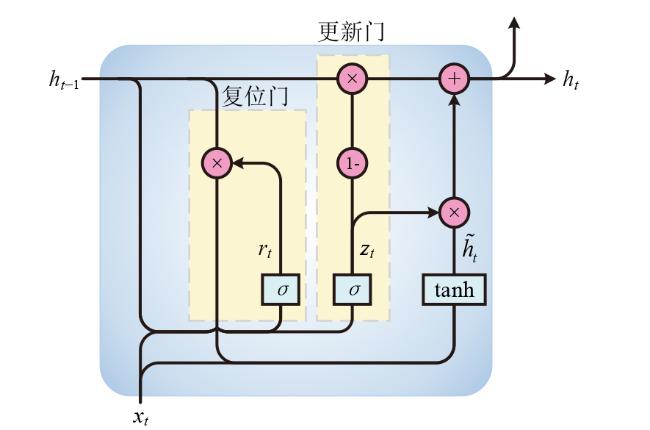
正交试验被广泛用于多因素多水平复杂实验的数值模型构建和相关参数寻优[24-28]。其具体步骤为：首先，使用一系列试验设计，得到在设计变量（因素）不同水平下的输出变量结果；随后，在试验结果的基础上进行数值建模，将设计变量与输出变量之间的非线性关系通过数学关系式或黑盒模型替代[25]。本文设计变量包括环境温度、负载率和散热风机风速，输出变量包括变压器高压绕组外侧平均温度和散热口平均温度。

3.2 贝叶斯-GRU模型

门控循环单元（gate recurrent unit, GRU）具有训练效率高、过拟合概率低的优点[29]。GRU网络结构如图2所示，其数学描述为：
$\left\{\begin{array}{l}r_{t}=\sigma\left(W_{\mathrm{r}} \cdot\left[h_{t-1}, x_{t}\right]\right) \\z_{t}=\sigma\left(W_{\mathrm{z}} \cdot\left[h_{t-1}, x_{t}\right]\right) \\\tilde{h}_{t}=\tanh \left(W_{\bar{h}} \cdot\left[r_{t} \times h_{t-1}, x_{t}\right]\right) \\h_{t}=\left(1-z_{t}\right) \times h_{t-1}+z_{t} \times \tilde{h}_{t} \\y_{t}=\sigma\left(W_{\mathrm{o}} \cdot h_{t}\right)\end{array}\right.$
式中：xt、yt分别为输入和输出向量；ht −1和ht分别为上一时刻和当前时刻的状态记忆变量；h̃t为当前候选集的状态；rt为复位门的状态；zt为更新门的状态；Wr、Wz、Wh̃和Wo分别为复位门、更新门、候选集、输出向量与xt及ht−1构成的连接矩阵相乘的权重参数；σ为Sigmoid激活函数。
图2 GRU网络结构

Fig.2 Network structure of GRU

贝叶斯优化是一种超参数调整方法，常被用于黑盒函数的优化[30]。采用贝叶斯优化对GRU的三个超参数进行寻优，包括隐藏层数、初始学习率和正则化系数。

3.3 计算结果的评价

计算结果的准确度是评价神经网络模型优劣的指标。采用均方根误差（root mean square error, ERMSE）、平均绝对百分比误差（mean absolute percentage error, EMAPE）、决定系数R2作为评价指标，其表达式分别为：
$E_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\left(y_{i}-\hat{y}_{i}\right)^{2}}$
$E_{\mathrm{MAPE}}=\frac{100 \%}{n} \sum\left|\frac{y_{i}-\hat{y}_{i}}{y_{i}}\right|$
$R^{2}=1-\frac{\sum\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum\left(y_{i}-\bar{y}_{i}\right)^{2}}$
式中：n为样本数量；yi为真实值（仿真得到的结果）；$\hat{y}_{i}$为模型计算值；$\bar{y}_{i}$为样本均值。

4 案例分析

由于余热利用主要涉及变压器投运后的运行工况，因此，选取环境温度、负载率、散热风机风速三个因素来进行控制变量仿真实验。在COSMOL 6.1有限元仿真软件中导入建立的干式变压器模型，添加流场、磁场、电路和流体传热等多个物理场进行仿真，得到数值结果和温度分布云图。
首先对模型进行网格无关性验证。四个不同网格精度的检验组得到的仿真结果相较仿真组结果的偏差见表3。可以看出，不同精度的网格不会对仿真结果产生显著的影响。
表3 网格无关性验证结果

Table 3 Results of grid independence test

组别 偏差/%
铁芯热点温度 绕组热点温度 高压绕组外侧平均温度 散热口平均温度
细化网格组1 −0.16 −0.08 0.04 0.12
细化网格组2 1.12 −0.31 0.20 2.80
粗化网格组1 0.48 −0.39 0.01 −0.46
粗化网格组2 0.52 −0.08 0.01 −0.59

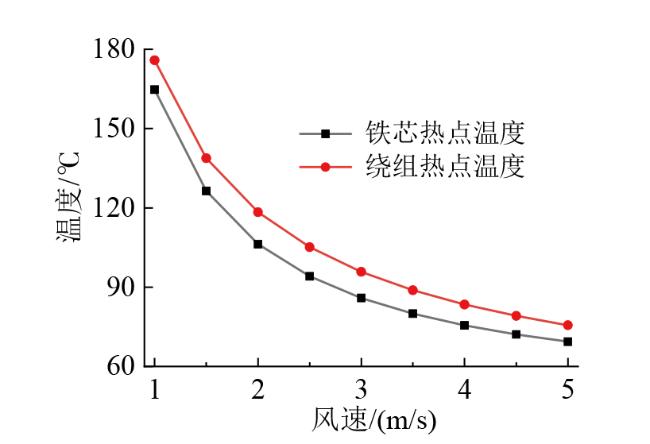
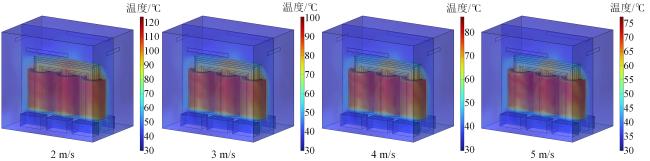
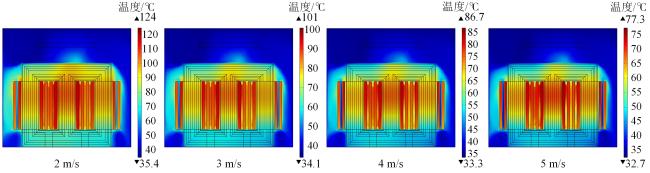
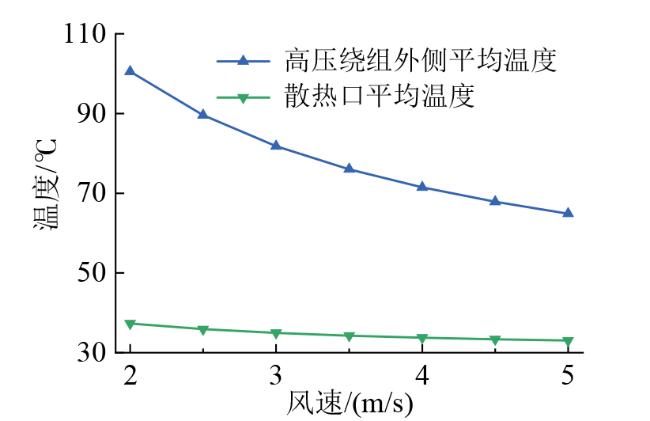
4.1 散热风机风速对温度分布的影响

固定环境温度为30 ℃、负载率为1.0，对干式变压器温度分布进行仿真，研究散热风机风速对其的影响。在不同风速下，空载损耗值恒定为1 266.8 W，负载损耗值恒定为7 117.8 W，其数值相对铭牌值误差较小，且与风速大小无关。
不同风速下干式变压器热点温度数值的变化规律如图3所示。当风速为1 m/s时，绕组热点温升超过限值（绝缘等级为F级的变压器在额定电流下的温升限值为100 K[31]），变压器无法长期稳定运行。当风速为2 m/s时，绕组热点温度为118.4 ℃，温升88.4 K，满足绝缘要求，变压器可以长期稳定运行。当风速为5 m/s时，绕组温升仅为45.6 K。可以看出，随着风机风速的增大，热点温度逐渐降低。
图3 散热风机风速对干式变压器热点温度的影响

Fig.3 Influence of cooling fan wind speed on hot spot temperature of dry-type transformer

当风机风速分别为2、3、4、5 m/s时，干式变压器温度空间分布云图和横切面分布云图分别如图4和图5所示。随着散热风机风速增大，干式变压器温度逐渐下降。四个场景下，绕组热点温度分别为118.4、95.8、83.5、75.6 ℃，热点均位于中心位置的B相低压绕组，外侧的高压绕组和没有绝缘包封的铁芯温度相对较低；变压器主体部分温度显著高于空气域，向空气中散发热量。
图4 不同风速时干式变压器温度空间分布云图

Fig.4 Temperature spatial distribution of dry-type transformer at different wind speeds

图5 不同风速时干式变压器温度横切面分布云图

Fig.5 Temperature cross section distribution of dry-type transformer at different wind speeds

散热风机风速为2 ~ 5 m/s时，高压绕组外侧平均温度和散热口平均温度的变化曲线如图6所示。风机风速为2 m/s时，高压绕组外侧平均温度为100.5 ℃，散热口平均温度为37.3 ℃；风速为5 m/s时，高压绕组外侧平均温度为64.9 ℃，空气域平均温度为33.0 ℃。
图6 不同区域温度随散热风机风速变化的规律

Fig.6 The change of temperature in different positions with the wind speed of the cooling fan

综上所述，风机风速较低时变压器温度较高，有利于获得品位更高的余热；然而，为了保证变压器的稳定运行，必须将变压器的主体温度维持在绝缘允许的范围内。但若风速过高，则会导致温度大幅下降，不利于余热利用。因此，在实际使用过程中，应着力寻求余热利用经济性和安全性的平衡点。在该案例中，当散热风机风速为2 m/s时，变压器主体温度符合绝缘要求；同时，较高的温度有利于余热利用的实施。

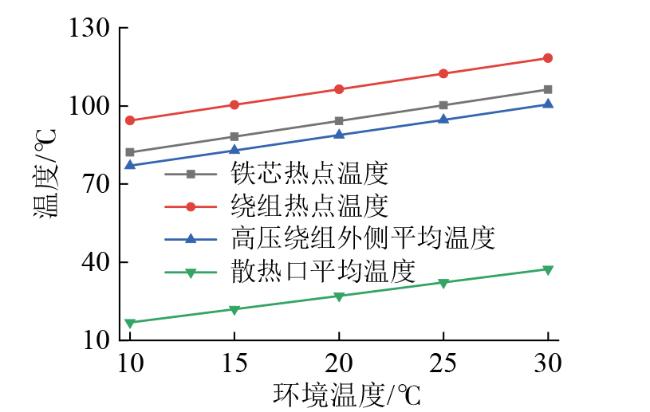
4.2 环境温度对温度分布的影响

设定风速恒为2 m/s，负载率恒为1.0，研究环境温度变化对温度分布的影响。类似地，在不同环境温度条件下，变压器的空载损耗和负载损耗均保持不变。
不同环境温度下干式变压器热点温度、高压绕组外侧平均温度和散热口平均温度的变化规律如图7所示。图中可见，环境温度对不同区域的影响近似线性。其中，散热口平均温度略高于环境温度。此外，在不同环境温度下，变压器各区域的温升基本维持在同一数值，即环境温度对温升没有显著影响。因此，环境温度对余热利用影响较小。
图7 不同区域温度随环境温度变化的规律

Fig.7 The change of temperature in different positions with ambient temperature

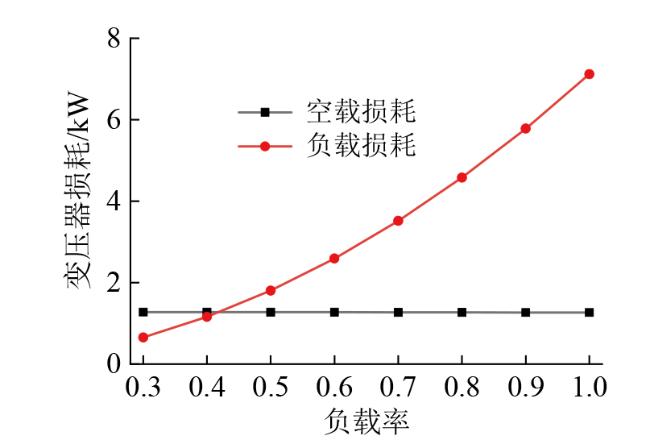
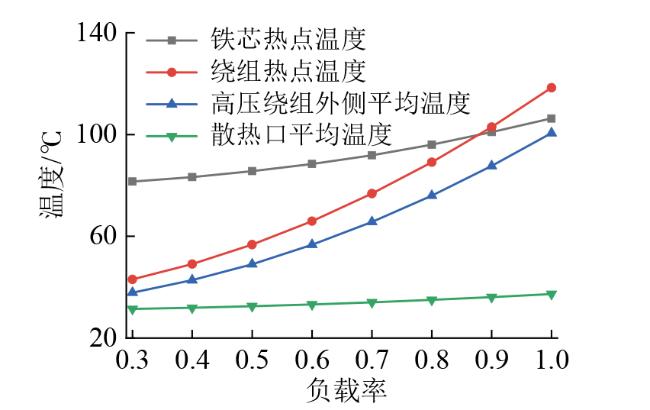
4.3 负载率对温度分布的影响

设定风速恒为2 m/s，环境温度恒为30 ℃，研究负载率变化对温度分布的影响。将负载率限定在0.3 ~ 1.0范围内。
变压器损耗随负载率变化的情况如图8所示。其中，空载损耗与负载率的取值无关，而负载损耗的数值与负载率的平方成正比。空载损耗与变压器带负荷多少无关，而负载损耗主要来源于变压器绕组的电阻发热，因此该结果与理论相符。
图8 变压器损耗随负载率变化的规律

Fig.8 The change of transformer loss with load rate

不同负载率下干式变压器热点温度、高压绕组外侧平均温度和散热口平均温度的数值变化规律如图9所示。一方面，负载率变化对绕组温度有显著影响，负载率较低时，绕组损耗较小，绕组温度比铁芯温度低，而随着负载率增大，绕组温度急剧上升；另一方面，负载率变化对铁芯温度的影响相对较小，主要是来自空气传热导致的温度上升。
图9 不同区域温度随负载率变化的规律

Fig.9 The change of temperature in different positions with load rate

综上所述，负载率越大，变压器温度越高，越有利于余热利用。但是为了保证变压器的稳定运行，必须将变压器的主体温度维持在绝缘允许的范围内。后续研究需要着力探索变压器负载率、绝缘要求和余热利用经济性等多因素的有效平衡。

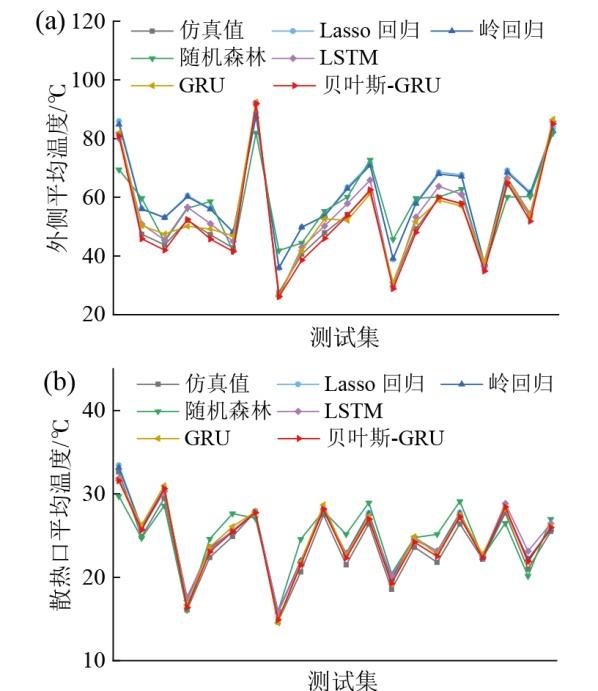
4.4 针对余热利用的干式变压器温度数值计算及检验

基于环境温度、负载率、散热风机风速三个因素进行正交试验。考虑到时间复杂度和实验实现难度，选取五个参数水平。表4给出了基于正交试验的不同参数组合和相应的温度数值仿真结果。
表4 正交试验结果

Table 4 Results of orthogonal experiment

样本序号 环境温度/℃ 负载率 散热风机风速/(m/s) 高压绕组外侧平均温度/℃ 散热口平均温度/℃
1 10 0.3 1 22.769 12.604
2 10 0.5 2 28.058 12.327
3 10 0.6 3 28.541 12.035
4 10 0.8 4 35.599 12.418
5 10 1.0 5 43.066 12.849
6 15 0.3 2 22.536 16.368
7 15 0.5 3 28.397 16.606
8 15 0.6 4 30.030 16.570
9 15 0.8 5 36.811 16.983
10 15 1.0 1 128.38 28.423
11 20 0.3 3 25.575 20.943
12 20 0.5 4 30.857 21.239
13 20 0.6 5 32.802 21.287
14 20 0.8 1 95.127 29.343
15 20 1.0 2 88.803 27.095
16 25 0.3 4 29.513 25.728
17 25 0.5 5 34.245 26.016
18 25 0.6 1 69.356 31.067
19 25 0.8 2 70.401 29.933
20 25 1.0 3 76.174 29.896
21 30 0.3 5 33.840 30.597
22 30 0.5 1 62.160 34.788
23 30 0.6 2 56.662 33.199
24 30 0.8 3 63.739 33.403
25 30 1.0 4 71.506 33.773
将表4的25组数据作为训练集；同时，在环境温度10 ~ 30 ℃、负载率0.3 ~ 1.0以及散热风机风速1 ~ 5 m/s的范围内随机生成了20组数据作为测试集，用以检验模型计算的准确性。基于MATLAB R2022b编写程序，对比了几种模型的计算结果，如图10所示。可见，针对高压绕组外侧平均温度，Lasso回归、岭回归和随机森林的计算结果准确性较低，而另外三者和仿真结果较为贴近；针对散热口平均温度，除随机森林准确度较低外，其他模型的计算结果均与仿真值接近。
图10 不同模型对高压绕组外侧平均温度（a）和散热口平均温度（b）的计算结果对比

Fig.10 Comparison of calculation results of the average temperature outside the high voltage winding (a) and the average temperature of the heat dissipation outlet (b) by different models

为了更直观地量化对比不同模型的计算结果，分别计算了不同模型的评价指标，见表5。
表5 不同模型计算结果的评价指标

Table 5 Evaluation indicators of calculation results of different models

模型 高压绕组外侧平均温度 散热口平均温度
ERMSE EMAPE/% R2 ERMSE EMAPE/% R2
Lasso回归 7.57 14.93 0.79 1.03 4.25 0.94
岭回归 7.36 14.72 0.80 1.01 4.17 0.95
随机森林 8.38 14.87 0.75 2.09 7.43 0.77
LSTM 2.70 4.74 0.97 1.10 4.58 0.94
GRU 2.22 3.91 0.98 0.98 3.76 0.95
贝叶斯-GRU 1.18 2.24 0.99 0.70 2.73 0.97
针对高压绕组外侧平均温度的数值计算，长短期记忆网络（long short-term memory, LSTM）和GRU具有较高的精度；针对散热口平均温度的数值计算，除了随机森林，其他四种单一方法均能取得较为准确的计算结果。在前五种单一方法中，GRU精度最高，而经过进一步改进的贝叶斯-GRU精度更高：计算高压绕组外侧平均温度时，贝叶斯-GRU的EMAPE约为2.24%，相比单一GRU降低了1.67%；计算散热口平均温度时，贝叶斯-GRU的EMAPE约为2.73%，相比单一GRU降低了1.03%。
综上所述，基于贝叶斯-GRU的温度分布数值计算模型精确度较高，可以较为准确地计算出变压器不同工况下的温度分布。在实际应用中，可结合变压器运行过程中的实测数据对神经网络进行训练，得到更加贴近真实工况的模型。

5 结论与展望

建立了10 kV干式变压器模型，并对其不同运行工况的温度分布进行了仿真计算。首先，分别讨论分析了散热风机风速、环境温度和负载率对干式变压器温度分布的影响。进一步地，设计正交试验，基于温度分布的仿真数据，对神经网络进行训练，得到计算干式变压器温度分布的通用数学模型。最后，在案例分析中对两个余热利用相关区域进行仿真测试，所采用的贝叶斯-GRU模型的EMAPE分别为2.24%和2.73%，R2分别为0.99和0.97，相较于单一的神经网络模型实现了大幅度的计算精度提升，具有较高的准确性和泛用性。
本文围绕变压器余热利用应该“从何处取热”这一问题展开，揭示了变压器在不同工况下的空间温度分布特征，为余热利用的取热策略提供了理论依据。后续研究可进一步探究运行工况对热量分布的影响，并基于实际变压器开展温度分布检测、数值模型构建与工程应用验证。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
陈胜, 卫志农, 顾伟, 等. 碳中和目标下的能源系统转型与变革:多能流协同技术[J]. 电力自动化设备, 2021, 41(9): 3-12. DOI: 10.16081/j.epae.202109037.

[2]
任松彦, 汪鹏, 林泽伟, 等. 不同碳达峰时点选择下的投资结构变化和经济社会影响——以广东省为例[J]. 新能源进展, 2022, 10(3): 280-290. DOI: 10.3969/j.issn.2095-560X.2022.03.013.

[3]
韩肖清, 李廷钧, 张东霞, 等. 双碳目标下的新型电力系统规划新问题及关键技术[J]. 高电压技术, 2021, 47(9): 3036-3046. DOI: 10.13336/j.1003-6520.hve.20210809.

[4]
卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. DOI: 10.7500/AEPS20200922001.

[5]
李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6258. DOI: 10.13334/j.0258-8013.pcsee.210050.

[6]
汪超群, 陈懿, 文福拴, 等. 电力系统碳排放流理论改进与完善[J]. 电网技术, 2022, 46(5): 1683-1691. DOI: 10.13335/j.1000-3673.pst.2021.2071.

[7]
张宁, 李姚旺, 黄俊辉, 等. 电力系统全环节碳计量方法与碳表系统[J]. 电力系统自动化, 2023, 47(9): 2-12. DOI: 10.7500/AEPS20221021001.

[8]
工业和信息化部办公厅, 市场监管总局办公厅, 国家能源局综合司. 工业和信息化部办公厅市场监管总局办公厅国家能源局综合司关于印发《变压器能效提升计划(2021-2023年)》的通知[EB/OL]. (2020-12-22)[2023-12-06]. https://www.gov.cn/zhengce/zhengceku/2021-01/17/content_5580512.htm.

[9]
曲友立, 强芸. 电力变压器余热回收可行性研究[J]. 电气应用, 2010, 29(5): 82-85.

[10]
汪筝, 黄磊, 王斌, 等. 水冷变压器的余热再利用[J]. 电力与能源, 2014, 35(3): 401-404. DOI: 10.3969/j.issn.2095-1256.2014.03.047.

[11]
杨作梁, 杨森. 利用电力变压器损耗为变电站房屋供暖探索[J]. 节能技术, 2015, 33(6): 559-561. DOI: 10.3969/j.issn.1002-6339.2015.06.016.

[12]
王志斌. 变压器顶层油温普查及余热利用分析[J]. 黑龙江电力, 2018, 40(1): 63-67, 93. DOI: 10.3969/j.issn.1002-1663.2018.01.013.

[13]
张焱, 邬振武, 徐林. 变电站主变压器余热利用型式分析[J]. 上海节能, 2021(9): 1020-1024. DOI: 10.13770/j.cnki.issn2095-705x.2021.09.017.

[14]
沈根. 变电站利用变压器余热的热泵供热系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.

[15]
CHIEN Z J, CHO H P, JWO C S, et al. A study of waste-heat recovery unit for power transformer[J]. Advanced material and manufacturing science, 2014, 875-877: 1661-1665. DOI: 10.4028/www.scientific.net/AMR.875-877.1661.

[16]
DOROTIĆ H, ČULJAK K, MIŠKIĆ J, et al. Technical and economic assessment of supermarket and power substation waste heat integration into existing district heating systems[J]. Energies, 2022, 15(5): 1666. DOI: 10.3390/en15051666.

[17]
王静, 陈炯聪, 赵宇明, 等. 干式变压器余热应用于制冷的技术可行性分析[J]. 现代制造技术与装备, 2023, 59(6): 24-28. DOI: 10.3969/j.issn.1673-5587.2023.06.010.

[18]
GUO J Y. The feasibility analysis of low-temperature waste heat thermoelectric power generation, based on forced oil circulation cooling transformer[C]// Proceedings of the 2015 Asia-Pacific Energy Equipment Engineering Research Conference. Zhuhai: PRC, 2015: 9-12.

[19]
LI Z M, ZHAO Y Q, LIU W, et al. Independent power generation in a modern electrical substation based on thermoelectric technology[J]. Journal of electronic materials, 2017, 46(5): 2557-2559. DOI: 10.1007/s11664-016-5054-8.

[20]
唐钊, 刘轩东. 基于热路模型的干式变压器绕组热点温度计算[J]. 电工技术, 2021(13): 24-28, 32. DOI: 10.19768/j.cnki.dgjs.2021.13.006.

[21]
张奇婧, 王浩名, 杜振斌, 等. 干式变压器绕组三维温度场与温升的数值分析[J]. 变压器, 2021, 58(3): 39-43. DOI: 10.19487/j.cnki.1001-8425.2021.03.007.

[22]
周海滨, 张正祥, 李文涛, 等. 干式变压器不同负载下绕组热点温度的计算与分析[J]. 变压器, 2022, 59(1): 1-5, 21. DOI: 10.19487/j.cnki.1001-8425.2022.01.001.

[23]
宓传龙. 变压器电抗器[M]. 北京: 中国电力出版社, 2021.

[24]
刘瑞江, 张业旺, 闻崇炜, 等. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010, 27(9): 52-55. DOI: 10.3969/j.issn.1002-4956.2010.09.016.

[25]
袁发庭, 杨文韬, 韩毅凛, 等. 基于电磁-流热双向耦合的变压器绕组温升计算及结构参数优化研究[J]. 高电压技术, 2024, 50(3): 952-961. DOI: 10.13336/j.1003-6520.hve.20221530.

[26]
刘江, 薛守洪, 胡学超, 等. 基于响应曲面法的变压器油T501电化学测试条件优化[J]. 热力发电, 2021, 50(11): 170-176. DOI: 10.19666/j.rlfd.202103029.

[27]
张良锐, 崔海亭, 马康乐, 等. 太阳能-生物质能联合供暖系统研究[J]. 新能源进展, 2022, 10(3): 249-257. DOI: 10.3969/j.issn.2095-560X.2022.03.009.

[28]
WANG X X, LIU S R, YE P L, et al. Study of a hybrid vehicle powertrain parameter matching design based on the combination of orthogonal test and cruise software[J]. Sustainability, 2023, 15(14): 10774. DOI: 10.3390/su151410774.

[29]
DEY R, SALEM F M. Gate-variants of Gated Recurrent Unit (GRU) neural networks[C]// 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS). Boston: IEEE, 2017: 1597-1600. DOI: 10.1109/MWSCAS.2017.8053243.

[30]
ABDAR M, POURPANAH F, HUSSAIN S, et al. A review of uncertainty quantification in deep learning: techniques, applications and challenges[J]. Information fusion, 2021, 76: 243-297. DOI: 10.1016/j.inffus.2021.05.008.

[31]
国家市场监督管理总局, 国家标准化管理委员会. 电力变压器第11部分: 干式变压器:GB/T 1094.11-2022[S]. 北京: 中国标准出版社, 2022.

Options
文章导航

/

〈 〉

主管单位：中国科学院
主办单位：中国科学院广州能源研究所
ISSN 2095-560X　
CN 44-1698/TK
地址：广州市天河区五山能源路2号广州能源所《新能源进展》编辑部　
邮编：510640　
电话：+86-20-87057066　
E-mail：xnyjz@ms.giec.ac.cn
微信公众号
粤ICP备11089167号-2　 版权所有 © 《新能源进展》编辑部