0 引言
近年来，海洋可再生能源利用成为各国的研究热点。波浪能能量密度高，分布范围广，受昼夜温差变化影响小，是海洋可再生能源的开发主体之一，20世纪90年代以来波浪能发电技术得到快速发展。振荡水柱式波浪能装置（oscillating water column wave energy converters, OWC WECs）由于转换结构简单、腐蚀风险小，主要运动部件与海水无直接接触，是目前技术发展最快的波浪能发电装置之一。
现阶段，振荡水柱式波浪能装置的研究集中在提高一级和二级能量转换效率上。其中，二级能量转换的核心部件是空气透平，包括威尔斯式[1]和冲击式[2]两种。后者在工程应用中占据较大比例。近年来，为提高冲击式透平的效率和可靠性，许多学者将研究热点集中在冲击式透平的叶片翼型、数量、布置方式、叶尖结构[3-5]，并取得了阶段性成果。在大流量和高转速下，叶片被诱导后极易发生自激振动，比如颤振，使叶片发生气动弹性动力学失稳，叶片疲劳破坏，出现裂纹，进而发生断裂。目前研究人员已开展许多针对叶片颤振问题的研究。李贝等[6]开展了临界颤振速度主导因素的研究。姚志峰等[7]使用嵌套网格技术对叶片振动类问题进行数值模拟，解决了叶片振动模拟中大变形引起的网格负体积问题。董旭等[8]基于二维平板叶栅，对攻角、安装角、振动模态等影响叶片颤振的参数进行了研究。郑赟等[9]采用影响系数法研究了动静叶轴向间距对叶片颤振特性的影响规律，发现轴向间距的减小增大了静叶对动叶叶片震动的影响范围。
为提高振荡水柱式波浪能装置防腐性能和起动性能，叶片采用玻璃纤维制造。但是由于这类材料硬度及质地均比金属材料差，结构阻尼小得多，更容易出现颤振现象。然而，针对冲击式透平材料性能引起的颤振问题，鲜有文献资料提及。本文研究颤振对冲击式透平的影响，以单向整流冲击式空气透平为研究对象，求解透平动叶的结构动力学方程和流体的三维非定常纳维−斯托克斯方程（Navier-Stokes equation, N-S方程），改进了原有透平的相关几何参数，并对优化前和优化后的透平分别进行数值模拟。使用CARTA[10]提出的能量法，基于透平预应力模态分析的结果，建立双通道流场模型，对冲击式透平的叶片颤振进行预测。
1 数值模拟理论
1.1 控制方程
由于波浪低频特性，振荡水柱式波浪能装置气室内往复气流速度较低，透平与空气之间温差也较小。将空气视为不可压缩流体，不考虑能量方程的影响，求解连续性方程和动量方程：
$\frac{\partial u_{i}}{\partial x_{i}}=0$
$\begin{aligned}\frac{\partial u_{i}}{\partial t}+\frac{\partial u_{i} u_{j}}{\partial x_{j}}= & \frac{\partial}{\partial x_{j}}\left[\mu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)\right]- \\& \frac{1}{\rho} \frac{\partial p}{\partial x_{i}}+f_{i}\end{aligned}$
式中：$ u_{i}$为流体速度；$ x_{i}$表示笛卡尔坐标；i、j为张量下标，取1、2、3；ρ为流体密度；μ为空气的动力黏度；p为压力；f为质量力。
透平动叶片的结构动力学方程为：
$\ddot{y}+2 \zeta \omega_{\mathrm{n}} \dot{y}+\omega_{\mathrm{n}}^{2} y=F(t)$
式中：y、$ \dot{y}$、$ \ddot{y}$分别为结构振动的位移、速度、加速度；$ \zeta$为阻尼比；$ \omega_{\mathrm{n}}$为振动频率；F(t)为载荷力。
1.2 湍流模型
SST k-ɷ剪切应力传输模型结合了标准k-ɷ和标准k-ε的优势，在远离壁面的主流区使用k-ε模型，在边界层区域使用k-ɷ模型，是对旋转机械进行数值模拟的通用湍流模型。由于SST k-ɷ模型可处理边界层分离现象，同时可避免使用壁面函数带来的不准确性，本次研究使用该模型。为使N-S方程封闭，SST k-ɷ湍流模型额外引入了以下两个方程：
$\left\{\begin{array}{c}\rho \frac{\partial k}{\partial t}+\rho \frac{\partial\left(k u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left(\Gamma_{k} \frac{\partial k}{\partial x_{j}}\right)+G_{k}-Y_{k}+S_{k} \\\rho \frac{\omega}{\partial t}+\rho \frac{\partial\left(\omega u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left(\Gamma_{\omega} \frac{\partial k}{\partial x_{j}}\right)+G_{\omega}-Y_{\omega}+ \\D_{\omega}+S_{\omega}\end{array}\right.$
式中：k和ɷ分别为湍流动能和湍流动能比耗散率；$ \Gamma_{k}$和$ \Gamma_{\omega}$分别为k和ɷ的扩散系数；G为产生项；Y为耗散项；S为源项；D为交叉扩散项。
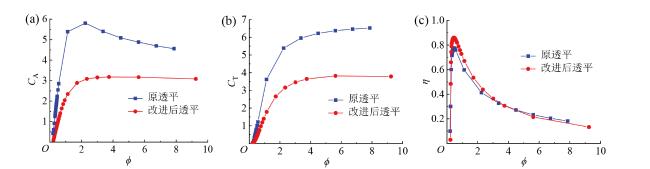
1.3 透平性能评价参数
$C_{\mathrm{A}}=\frac{2 \Delta p q}{\rho\left(v_{\mathrm{a}}^{2}+U_{\mathrm{R}}^{2}\right) b l_{\mathrm{r}} r_{\mathrm{N}} v_{\mathrm{a}}}$
$C_{\mathrm{T}}=\frac{2 T}{\rho\left(v_{\mathrm{a}}^{2}+U_{\mathrm{R}}^{2}\right) b l_{\mathrm{r}} r_{\mathrm{N}} r_{\mathrm{R}}}$
$\phi=\frac{v_{\mathrm{a}}}{U_{\mathrm{R}}}$
$\eta=\frac{T \omega}{\Delta p q}=\frac{C_{\mathrm{T}}}{\phi C_{\mathrm{A}}}$
式中：va为进口气流速度；UR为透平50%叶高处的旋转速度；q为流量；Δp为进出口之间的压力差；rN为动叶片个数；b、lr、rR分别为叶片高度、弦长、和50%叶高对应的半径，均为透平代表性的几何长度；T为叶片受到的扭矩。
2 数值模拟模型
2.1 透平结构参数
以中国科学院广州能源研究所研发的波浪能发电装置BD104G的单向整流冲击式透平为研究对象，进口导流叶片和动叶片见图1。
基于现有透平在运行中发现的效率不高、效率随流量系数下降很快等问题，对透平几何参数和动叶片个数进行了改进。改进后的透平动叶使用NACA4412翼型，相比原透平，优化了气流进出口角和安装角，将直叶片改为三维扭转叶片，具体参数见表1。
表1 优化前与优化后透平的几何参数Table 1 Geometry parameters of turbines before and after optimization |
| 项目 | 原透平 | 优化后的透平 |
|---|---|---|
| 静叶出口角/(°) | 15.0 | 30.0 |
| 动叶进口角/(°) | 42.5 | 57.3 |
| 动叶出口角/(°) | 28.6 | 22.9 |
| 动叶安装角/(°) | 70.0 | 52.1 |
| 静叶数量 | 28 | 31 |
| 动叶数量 | 34 | 37 |
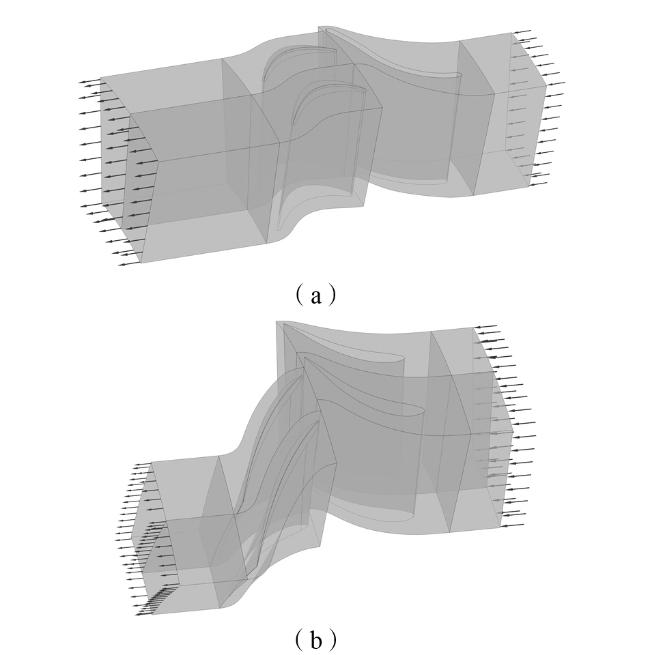
2.2 瞬态叶栅模型
为提高计算效率，使用双通道模型开展叶片颤振的数值模拟。建立的计算流体动力学（computational fluid dynamics, CFD）模型见图2。
2.3 网格划分与无关性验证
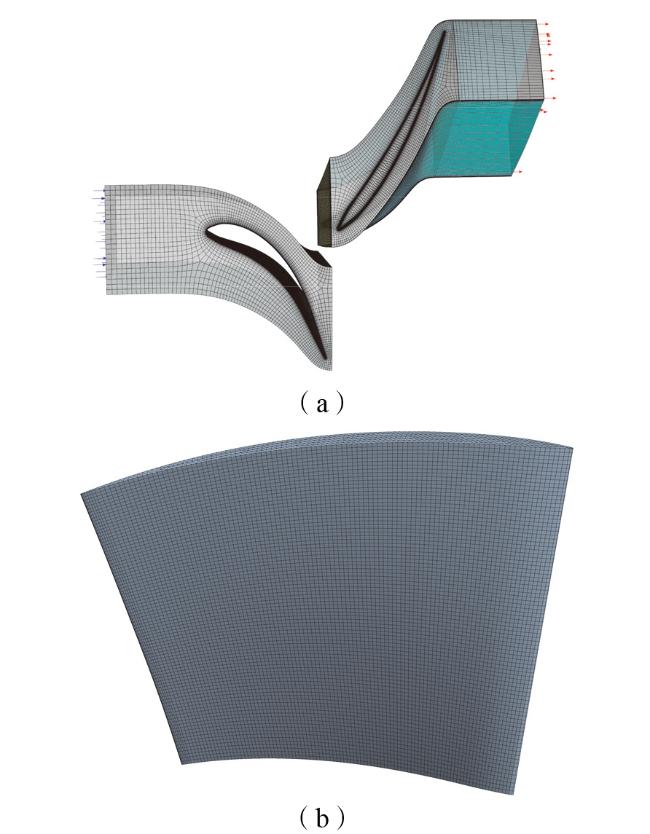
2.3.1 网格划分
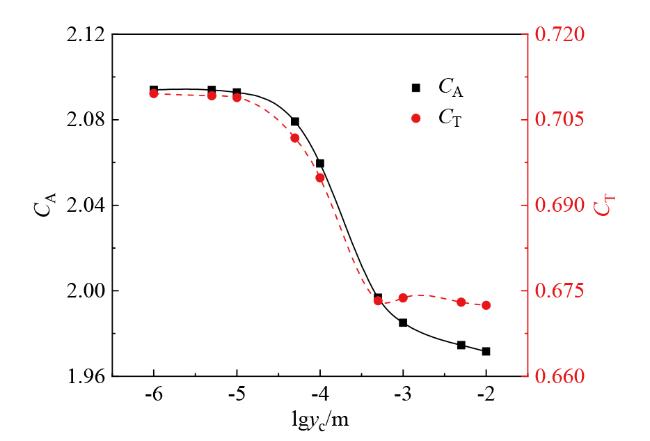
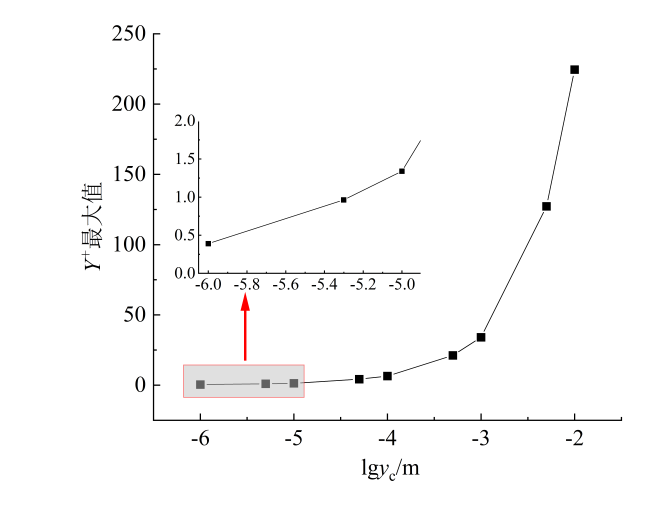
2.3.2 网格无关性
为保证计算结果的准确性，须进行网格无关性校验。使用图3（a）中的单流道网格进行透平稳态数值模拟，以验证网格无关性。湍流模型以及壁面处理方法对近壁区域网格提出了不同的要求。为使结论具有通用性，引入无量纲的Y+，表示近壁区域网格的细化程度，可定义为壁面附近第一层网格的无量纲厚度：
$Y^{+}=\frac{y_{\mathrm{c}}}{\mu} \sqrt{\rho \tau_{\mathrm{w}}}$
表2展示了某工况下，固定yc = 1 × 10−5 m，仅改变整体网格数量时数值模拟的结果。固定yc到合适的值之后，改变总体网格数量并不显著影响数值模拟的准确性，综合考虑准确性和计算效率，选择yc = 1 × 10−5 m，单流道网格数量280 000个，作为以下一系列计算的基准。
表2 CA和CT随网格数量的变化关系Table 2 Variation of CA and CT with grid number |
| 网格数 | CA | CT |
|---|---|---|
| 210 000 | 1.645 9 | 0.604 83 |
| 280 000 | 1.644 6 | 0.604 61 |
| 400 000 | 1.643 8 | 0.604 36 |
| 560 000 | 1.646 1 | 0.605 31 |
| 720 000 | 1.645 5 | 0.605 08 |
3 结果分析
3.1 刚性叶片性能分析
原有透平和改进后透平的相关性能参数见图6。原透平已达到较高的能量转换效率，流量系数ϕ为0.45时达到峰值效率77.60%。透平改进后，CA和CT均有下降，但峰值效率有所提高，ϕ达到0.48时获得峰值效率86.02%。此外，改进后的透平高效率流量系数区间有所增大，但大流量系数下效率稍微降低。
两种透平在最佳效率点的压力分布见图7。原透平上游总压力高达272 Pa，而改进后透平上游总压力仅180 Pa，这也是透平CA发生下降的原因。气流流经静叶，总体上叶尖压力大于叶根压力。气流流经进口导流叶片后，均发生明显的降压加速过程，在动叶压力侧和吸力侧形成了复杂的压力分布。动叶流域存在负压区域，原透平此区域最低压力达 −202 Pa，而改进后此区域最低压力仅 −50 Pa。注意到改进后的透平在进口导流叶片出口端存在一低压区，可能在此形成回流，未来应加以改进。
3.2 叶片颤振预测
3.2.1 模态分析
3.2.2 气动阻尼分析
4 结论
通过求解振荡水柱式波浪能装置透平单流道网格的三维定常N-S方程、动叶片的结构动力学方程，开展了数值模拟，对改进后透平的性能进行了预测，获得动叶的振动频率和相关振型。主要结论如下：
（1）透平的最高效率从77.60%增大到86.02%，高效率工况对应的流量系数范围也有所增大，性能显著提高。
（2）能量法可预测透平的颤振情况，动叶片基本不存在颤振问题，气弹稳定性较好，但在某些工况下，模态气动阻尼接近于0，在相近工况下可能会出现气弹不稳定问题。
