0 引言
近年来,染料敏化太阳能电池（dye sensitized solar cells, DSSC）由于其制造工艺简单、材料来源广泛、价格低廉等受到了很多关注[1,2]。这些优于传统硅和薄膜光伏器件的特点,使得DSSC可用于大规模生产。DSSC主要是由光阳极、电解质和对电极组成的“三明治”式结构。其中光阳极由导电玻璃、多孔纳米二氧化钛（TiO2）或其他的半导体氧化物层,吸附在TiO2的染料分子吸收层构成。当染料分子吸收太阳光时,电子从基态跃迁到激发态,处于激发态的电子不稳定,以非常快的速率注入到较低能级的TiO2导带中,注入导带中的电子从半导体电流流出,经外电路时做功,产生工作电流,并流回到对电极;空穴则留在氧化钛染料分子中被电解液中的氧化还原对还原,至此整个电路得到再生并完成一个光电化学反应循环[3,4,5]。
DSSC性能主要取决于电池薄膜对光的高效吸收和电子在回路中的高效传输。本文基于扩散理论建立了DSSC的连续性方程,使用适合于TiO2作为光阳极的内部参数,对DSSC电子注入和传输的内在机理进行研究。
1 光电子传输模型
1.1 连续性方程及边界条件
DSSC中TiO2颗粒尺寸很小,内部很难形成空间电荷分布,所以不考虑半导体薄膜内的内建电场,光生电子的传输是由浓度差引起的扩散传输[11,12]。TiO2薄膜厚度很薄（微米量级）,故假设同一平面上染料的吸附是均匀的,电子在其中的扩散可以看作是沿着垂直于TCO/TiO2（x方向）界面的一维扩散[13]。考虑一束单色光从TiO2电极面入射,在扩散电流${{J}_{n}}\left( x \right)$方向上取一厚度为Δx的微元控制体,如图1所示,在这个体积内设电子产生速率为G,电子复合速率为U,运用电荷守恒定律,得到光生电子的连续扩散微分方程：产生 + 流入 - 流出 - 消耗 = 累积,对应方程式如式（1）。
$G+\left[ -\frac{{{J}_{n}}\left( x+\Delta x \right)}{e} \right]-U-\left[ -\frac{{{J}_{n}}\left( x \right)}{e} \right]=\frac{\partial n}{\partial t}$ (1)
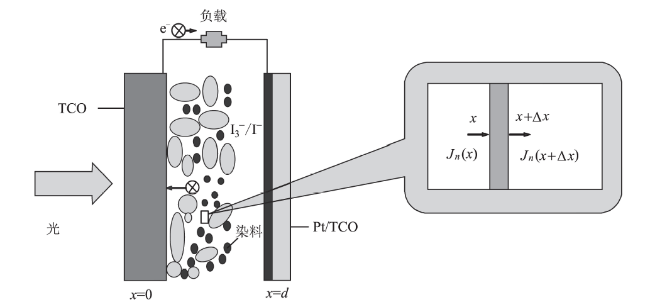
Fig. 1 DSSC schematic and enlarged micro-control body model图1 DSSC原理图及放大的微元控制体模型 |
根据Fick定律
${{J}_{n}}\left( x \right)=e{{D}_{n}}\frac{\text{d}n}{\text{d}x}$ (2)
${{J}_{n}}\left( x+\Delta x \right)={{J}_{n}}\left( x \right)+\frac{\partial {{J}_{n}}}{\partial x}\text{d}x$ (3)
式中：e为电子电量,e = 1.602 189 2 × 10-19 C;D为电子扩散系数;d为TiO2电极厚度。
光生电子注入TiO2速率：
$G=\mathop{\int }^{}\alpha \left( \lambda \right)\phi \left( \lambda \right)\text{exp}\left[ -\alpha \left( \lambda \right)x \right]\text{d}x$ (4)
仅考虑单色光：
$G=\alpha \phi \text{exp}\left( -\alpha x \right)$ (5)
式中：ϕ为透过导电衬底后的光子数;α为染料敏化TiO2膜的有效吸收系数。
为了简化分析过程,一般将复合速率常数与电子密度n看作是一级反应
$U=\frac{n\left( x \right)-{{n}_{0}}}{\tau }$ (6)
式中：n0为暗平衡电子密度;n(x)为导带中电子密度;τ为TiO2导带中电子寿命。
由式（1）~ 式（6）得到n(x) 的非齐次线性微分方程：
$D\frac{{{\partial }^{2}}n\left( x \right)}{\partial {{x}^{2}}}-\frac{n\left( x \right)-{{n}_{0}}}{\tau }+\alpha \phi \text{exp}\left( -\alpha x \right)=\frac{\partial n}{\partial t}$ (7)
稳态条件下,上式变为
$D\frac{{{\partial }^{2}}n\left( x \right)}{\partial {{x}^{2}}}-\frac{n\left( x \right)-{{n}_{0}}}{\tau }+\alpha \phi \text{exp}\left( -\alpha x \right)=0$ (8)
短路条件边界条件：
$n\left( 0 \right)={{n}_{0}}$ (9)
${{\left. \frac{\text{d}n}{\text{d}x} \right|}_{x=d}}=0$ (10)
光电池的开路电压与氧化还原对的电势和TiO2费米能级有关,TCO/ TiO2界面（x = 0）处的电子密度增加到n,给出了新的边界条件：
$n\left( 0 \right)=n$ (11)
1.2 电池输出参数1.3 模型验证
由上述方程及边界条件得到短路条件电流密度Jsc：
${{J}_{\text{sc}}}=\frac{e\phi L\alpha }{1-{{L}^{2}}{{\alpha }^{2}}}\left[ -L\alpha +\tanh \left( \frac{d}{L} \right)+\frac{L\alpha \text{exp}\left( -\text{d}\alpha \right)}{\cosh \left( \frac{d}{L} \right)} \right]$ (12)
其中,L表示扩散长度
$L=(D \tau)$½ (13)
输出电流为：
$J={{J}_{\text{sc}}}-\frac{eD{{n}_{0}}}{L}\tanh \left( \frac{d}{L} \right)\left[ \exp \left( \frac{eV}{kTm} \right)-1 \right]$ (14)
式中：m为理想因子。
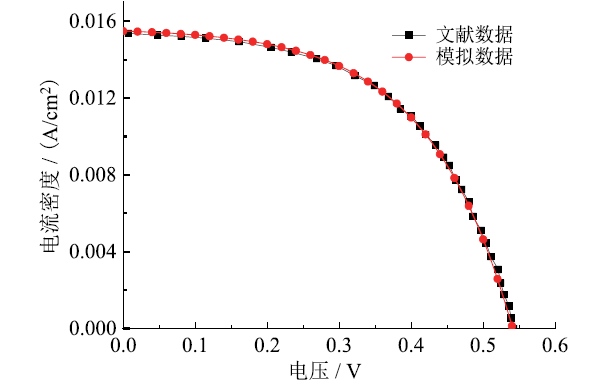
Fig. 2 J-V curve of DSSC图2 DSSC的J-V曲线 |
Table 2 Simulation results for the default DSSC表2 默认DSSC的模拟结果 |
| Jsc / (A/cm2) | VOC / V | Pmax / (W/cm2) | η / % |
|---|---|---|---|
| 0.0154 | 0.5405 | 0.0044 | 4.43 |
2 结果与讨论
2.1 不同温度条件下DSSC的光电性能2.2 不同膜厚条件下DSSC的光电性能
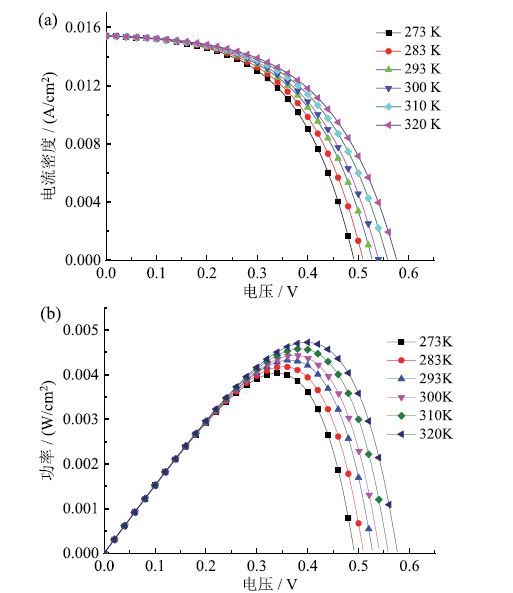
Fig. 3 J-V (a) and P-V (b) curves of DSSC at different temperatures图3 不同温度下DSSC的J-V（a）和P-V（b）曲线 |
Table 3 DSSC simulation results at different temperatures表3 不同温度下DSSC模拟结果 |
| T / K | Jsc / (A/cm2) | VOC / V | Pmax/ (W/cm2) | η / % |
|---|---|---|---|---|
| 273 | 0.015 4 | 0.491 9 | 0.004 0 | 4.03 |
| 283 | 0.015 4 | 0.509 9 | 0.004 2 | 4.18 |
| 293 | 0.015 4 | 0.527 9 | 0.004 3 | 4.33 |
| 300 | 0.015 4 | 0.540 5 | 0.004 4 | 4.43 |
| 310 | 0.015 4 | 0.558 5 | 0.004 6 | 4.58 |
| 320 | 0.015 4 | 0.576 5 | 0.004 7 | 4.73 |
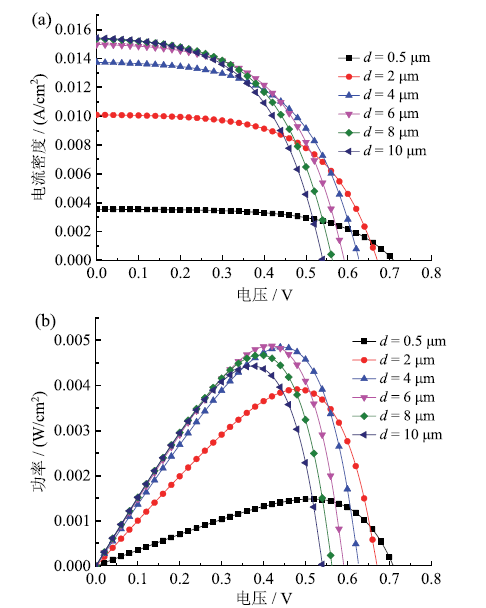
Fig. 4 J-V (a) and P-V (b) curves of DSSC under different film thicknesses图4 不同膜厚下DSSC的J-V（a）和P-V（b）曲线 |
Table 4 DSSC simulation results of different film thicknesses表4 不同膜厚DSSC模拟结果 |
| d / μm | Jsc / (A/cm2) | VOC / V | Pmax / (W/cm2) | η / % |
|---|---|---|---|---|
| 0.5 | 0.003 5 | 0.709 6 | 0.001 5 | 0.48 |
| 2.0 | 0.010 1 | 0.670 6 | 0.003 9 | 3.91 |
| 4.0 | 0.013 7 | 0.626 8 | 0.004 8 | 4.85 |
| 6.0 | 0.015 0 | 0.591 5 | 0.004 9 | 4.88 |
| 8.0 | 0.015 4 | 0.563 2 | 0.004 7 | 4.67 |
| 10.0 | 0.015 2 | 0.540 5 | 0.004 4 | 4.43 |
主要原因是随着光阳极膜厚的增加,光阳极薄膜吸附的染料分子量增加,从而使染料分子吸收更多的光子,产生更多的光生电子数,更多的光生电子会注入半导体导带中,导致Jsc的增加。膜厚到达一定值时,多孔薄膜吸附的染料量已足够多,达到饱和状态不再吸附,光生电子在被电极收集之前,经过的路径延长,增加了与电解质复合的概率。同时,膜厚的增加,增大了注入电子在传输过程中电子陷阱及表面态复合机会,使暗电流和表面电流增加,光电压下降。因而对于多孔薄膜电极应该有一个最佳膜厚。多孔薄膜厚度是DSSC宏观特性参数,可以通过丝网目数、印刷次数等工艺手段加以控制。
2.3 不同电子寿命条件下DSSC的光电性能2.4 不同电子扩散系数条件下DSSC的光电性能2.5 不同光照强度条件下DSSC的光电性能2.6 不同吸收系数条件下DSSC的光电性能
由于电子寿命的会影响DSSC性能,对τ = 1 ms、5 ms、10 ms、15 ms、20 ms进行模拟研究。短路电流密度Jsc和最大功率点在不同电子寿命时的变化情况如图5所示。结果表明,随着电子寿命的延长,短路电流密度和功率都随之增大,这是由于一个性能比较好的DSSC,需要在动力学上有一个和输运过程相比慢速的复合反应过程,电子在传输中复合反应的减少才会使电子寿命的延长。注入导带后的电子将在浓度梯度作用下向着导电衬底的方向扩散,电子需要一定的时间才能够到达导电衬底,在传输过程中有可能被复合而损失,导致导电衬底并不能接收全部电子,若想提高收集效率,一定要抑制复合过程,同时加快电子的传输。如表5所示,短路电流密度和光电转换效率的变化趋势相一致。研究表明,薄膜包覆几乎可以完全抑制表面陷阱态复合,同时可以减慢导带发生复合的速率,使DSSC的电子寿命有较明显的延长。
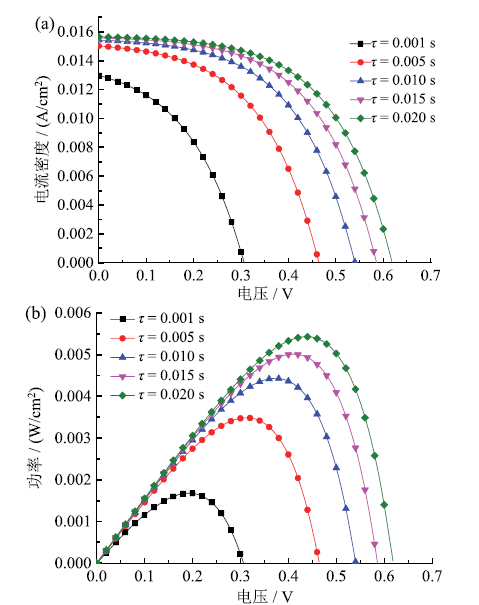
Fig. 5 J-V (a) and P-V (b) curves of different electronic lifetime DSSC图5 不同电子寿命DSSC的J-V曲线（a）和P-V曲线 |
Table 5 DSSC simulation results for different electronic lifetimes表5 不同电子寿命下DSSC模拟结果 |
| τ / ms | Jsc / (A/cm2) | VOC / V | Pmax / (W/cm2) | η / % |
|---|---|---|---|---|
| 1 | 0.013 0 | 0.306 5 | 0.001 7 | 1.68 |
| 5 | 0.015 0 | 0.464 5 | 0.003 5 | 3.49 |
| 10 | 0.015 4 | 0.540 5 | 0.004 4 | 4.43 |
| 15 | 0.015 6 | 0.586 1 | 0.005 0 | 5.01 |
| 20 | 0.015 7 | 0.618 7 | 0.005 4 | 5.43 |
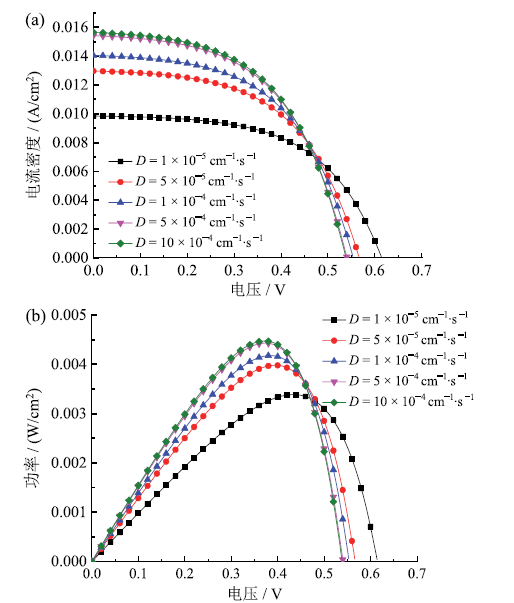
Fig. 6 J-V (a) and P-V (b) curves of DSSC under different diffusion coefficients图6 不同电子扩散系数下DSSC的J-V（a）和P-V（b）曲线 |
Table 6 DSSC simulation results under different electron diffusion coefficients表6 不同电子扩散系数下DSSC模拟结果 |
| D / (cm-1∙s -1) | Jsc / (A/cm2) | VOC / V | Pmax / (W/cm2) | η / % |
|---|---|---|---|---|
| 1 × 10-5 | 0.009 8 | 0.614 8 | 0.003 4 | 3.390 |
| 5 × 10-5 | 0.013 0 | 0.566 8 | 0.004 0 | 3.980 |
| 1 × 10-4 | 0.014 1 | 0.553 8 | 0.004 2 | 4.180 |
| 5 × 10-4 | 0.015 4 | 0.540 5 | 0.004 4 | 4.430 |
| 10 × 10-4 | 0.015 7 | 0.538 6 | 0.004 5 | 4.447 |
图7为不同光照强度下DSSC的J-V曲线和P-V曲线。当光照强度增加时,短路电流密度、开路电压和最大功率点都大幅度增加。光照强度对DSSC性能的影响较大。光生电流密度和光生电压随入射光强的这种变化主要是由于随着光照强度的增加,染料可以吸收的光子数增多,光生电子数增多,注入薄膜的电子数增多,短路电流密度增大。同时,在很宽的光谱范围内,光电子的收集速率基本上保持不变,相对于弱光照射,强光照射下产生更多的光电子,被收集需要更长的时间,因此多孔薄膜中累积的光电子数增多,以至于光阳极半导体的费米能级增加,电池的开路电压增大。由表7可知,DSSC的光电转换效率随光照强度的增加而增加,其变化趋势与Jsc相一致。
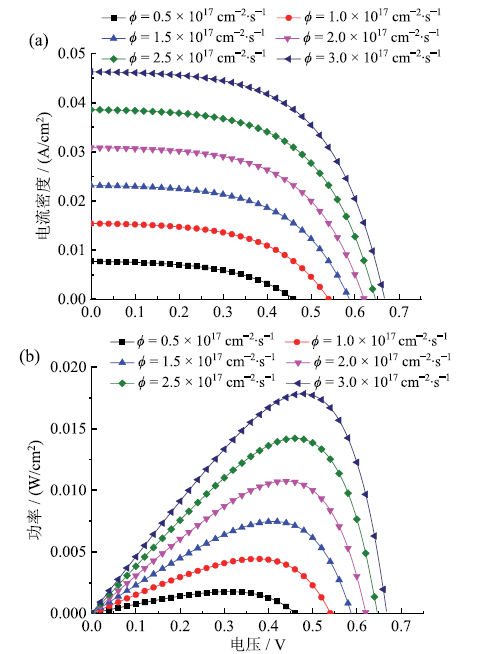
Fig. 7 J-V (a) and P-V (b) curves of DSSC under different light intensities图7 不同光照强度下DSSC的J-V（a）和P-V（b）曲线 |
Table 7 DSSC simulation results under different light intensities表7 不同光照强度下DSSC模拟结果 |
| ϕ / (cm-2∙s-1) | Jsc / (A/cm2) | VOC / V | Pmax / (W/cm2) | η / % |
|---|---|---|---|---|
| 0.5×1017 | 0.007 7 | 0.460 9 | 0.001 8 | 1.77 |
| 1.0×1017 | 0.015 4 | 0.540 5 | 0.004 4 | 4.43 |
| 1.5×1017 | 0.023 1 | 0.587 3 | 0.007 5 | 7.47 |
| 2.0×1017 | 0.032 9 | 0.620 6 | 0.010 7 | 10.75 |
| 2.5×1017 | 0.038 6 | 0.646 5 | 0.014 2 | 14.22 |
| 3.0×1017 | 0.046 3 | 0.667 7 | 0.017 8 | 17.84 |
图8所示为不同吸收系数下DSSC的J-V曲线和P-V曲线,吸收系数反映了多孔薄膜/染料电极对光的吸收能力。由图可知,当光吸收系数增大时,短路电流密度、开路电压和最大功率点都随之缓慢增大,这主要是由于有效吸收系数α反映了多孔薄膜对光的吸收能力,吸收系数越大, 多孔薄膜对光的吸收能力越强,吸收的光子数增加,光生电子数增大,注入薄膜的电子数增多,短路电流密度增大。同样,由式（4）可以看出,在吸收过程中吸收系数位于指数的位置,为了获得光生电子的显著变化,吸收系数的变化通常为100倍甚至更多。由表8知,DSSC的光电转换效率随吸收系数增大而升高,其变化趋势与Jsc相一致。一般来说化学染料如N719、N3染料等的吸收系数高于天然染料的吸收系数。
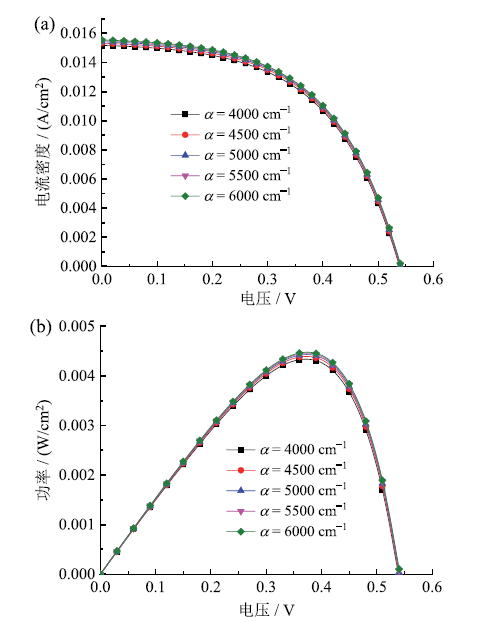
Fig. 8 J-V (a) and P-V (b) curves of DSSC with different absorption coefficients图8 不同吸收系数DSSC的J-V（a）和P-V（b）曲线 |
Table 8 DSSC simulation results under different absorption coefficients表8 不同吸收系数下DSSC模拟结果 |
| α / cm-1 | Jsc / (A/cm2) | VOC / V | Pmax / (W/cm2) | η / % |
|---|---|---|---|---|
| 4 000 | 0.015 2 | 0.538 6 | 0.004 3 | 4.34 |
| 4 500 | 0.015 3 | 0.539 7 | 0.004 4 | 4.39 |
| 5 000 | 0.015 4 | 0.540 5 | 0.004 4 | 4.43 |
| 5 500 | 0.015 5 | 0.541 0 | 0.004 5 | 4.46 |
| 6 000 | 0.015 5 | 0.541 4 | 0.004 5 | 4.48 |
3 结论
基于电子传输的扩散理论建立了DSSC的连续性方程,采用适用于TiO2作为光阳极的内部参数,借助MATLAB编程求解并模拟分析不同参数对电池内部结构的影响。结果表明,随着TiO2薄膜厚度的增加,DSSC的开路电压及光电转换效率均先增大后减小。此外,DSSC的光电转换效率随着工作温度、光照强度、电子寿命、电子扩散系数、吸收系数的增大均有一定程度的提高。该研究结果对未来DSSC的设计和实验具有一定的理论指导意义。