0 引言
1 实验部分
1.1 实验装置与材料
Fig. 1 Photos of the experimental apparatus图1 实验装置实物照片:(a)测试部分;(b)反应釜 |
1.2 实验步骤
2 含水合物沉积物电学参数频散特性
2.1 复电阻率参数计算
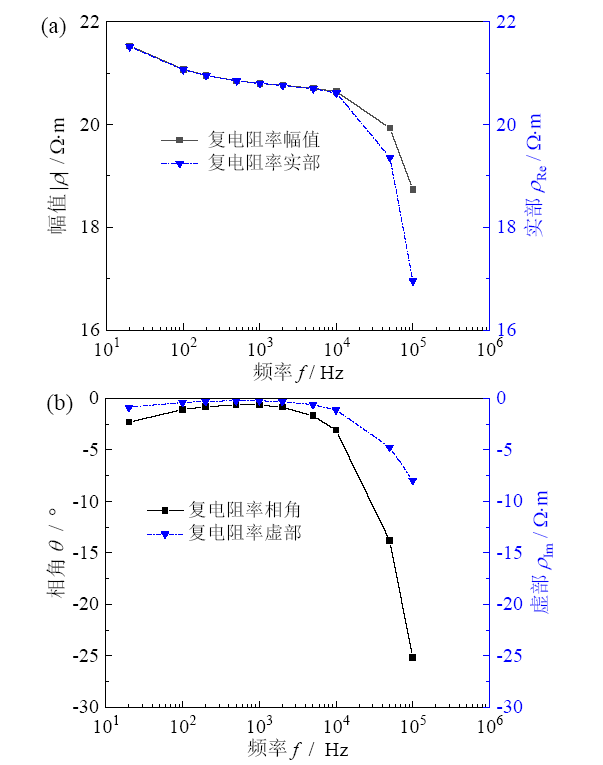
2.2 复电阻率参数频散特性
Fig. 2 Frequency dispersion curves of complex resistivity parameters图2 复电阻率参数频散曲线 |
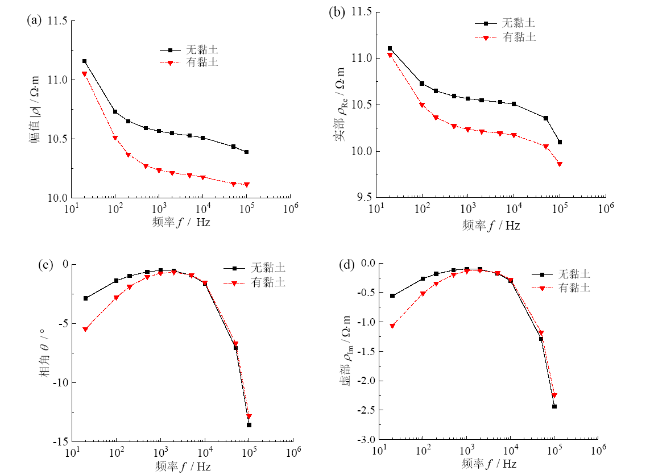
2.3 黏土的影响
Fig. 3 Frequency dispersion curves of complex resistivity parameters without and with clay图3 无黏土和有黏土条件下复电阻率参数的频散曲线 |
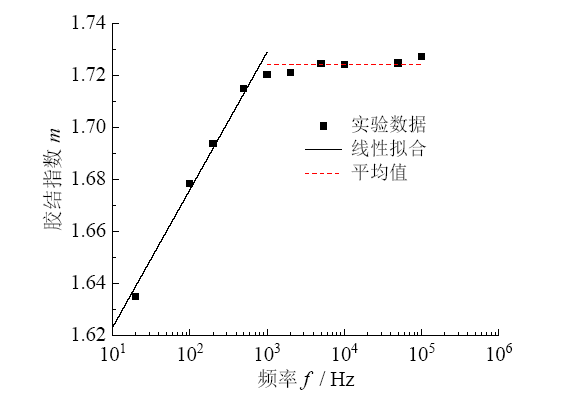
3 水合物饱和度计算模型
Fig. 4 Relationship between the cementation index m and frequency f图4 胶结指数m与频率f的关系曲线 |
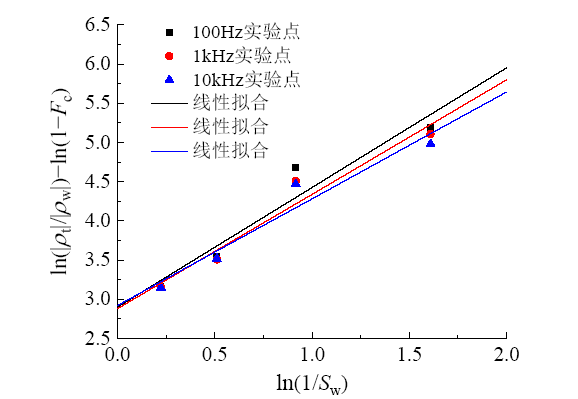
Fig. 5 Linear fitting of the experimental data at different testing frequencies图5 不同测试频率下实验数据的线性拟合 |
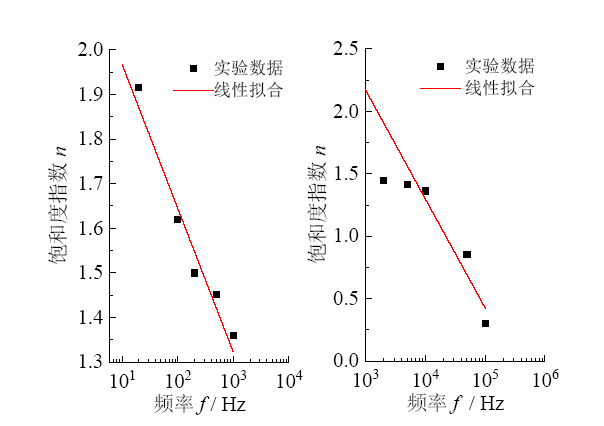
Fig. 6 Linear fitting of the saturation index n and frequency f图6 饱和度指数n与频率f的线性拟合 |