0 引言
因此,本文提出空气流动风阻网格模型结合热力学模型仿真的设计方法。该方法先采用空气流动风阻网格模型,以流速均匀性为优化目标,获得优化的电池结构,再采用热力学模型进行仿真求解,获得优化的电池模组的流场和温度场分布特性。该方法可以大大缩短设计的时间,也能够提供详细的设计信息。
1 建立模型
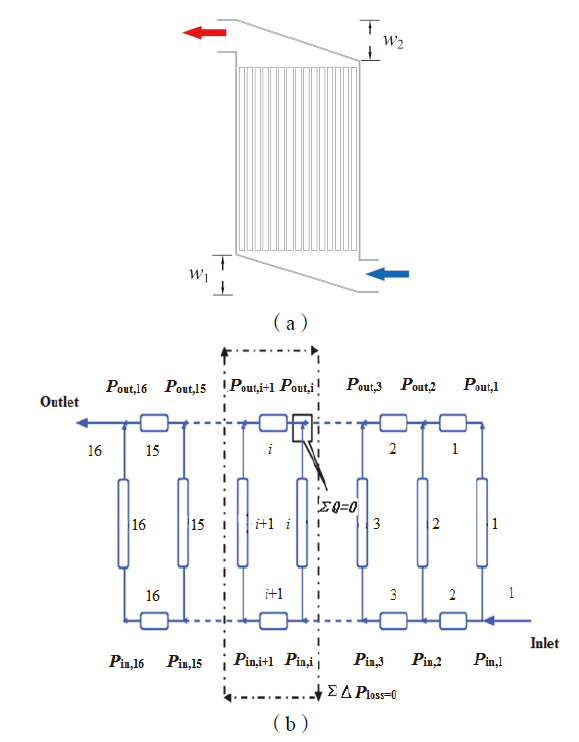
1.1 空气阻力网络模型
电池模组由15个软包电池平行排列,电池尺寸为W × L × T = 17 cm × 23 cm × 7 cm。电池间隔相等,均匀排列,间距为3 mm,因此共有16个垂直于入口水平方向的间隙通道。空气由风机推动,从下部进入,经导流板分流后分别进入电池模组壳体、电池单体之间的16个流道中。空气与电池模组的热交换方式主要是对流换热,而换热效果主要取决于流动中的空气流速和流量。为了实现电池模组的温度均匀性,则要求每个通道的流速和流量尽量一致,从而保证每个通道的冷却效果相同。本文主要通过改变上下挡板的角度,即通过调整导流板开口高度w1和w2的大小来调节每个通道中的空气流速,而且最大值不能超过5 cm,如图1a。
Fig. 1 (a) Structure schematic of the battery module; (b) flowing resistance network model of air图1 （a）电池模组结构示意图;（b）空气流动阻力网络模型 |
空气在流动过程中,受到沿程阻力和局部阻力的影响,导致压力以及流速发生变化。根据电池模组结构以及空气流动特点,建立空气流动阻力网格模型,如图1b。由于空气流速较小,可以认为是不可压缩流体。根据伯努利方程,可以知道第i个通道入口（出口）和相邻通道入口（出口）的压力关系：
${P_{m,i}} + \frac{1}{2}{\rho _{{\rm{air}}}}u_{m,i}^2 = {P_{m,i - 1}} + \frac{1}{2}{\rho _{{\rm{air}}}}u_{m,i - 1}^2 - \Delta {P_{{\rm{loss,}}m,i}}$ (1)
其中：u为空气的流速;ΔPloss为压力损失;m表示进口in或出口out。
第i个通道内部的压力关系为：
${P_{{\rm{in}},i}} + \frac{1}{2}{\rho _{{\rm{air}}}}u_{{\rm{in}},i}^2 = {P_{{\rm{out}},i}} + \frac{1}{2}{\rho _{{\rm{air}}}}u_{{\rm{out}},i}^2 + \Delta {P_{{\rm{loss,ch}},i}}$ (2)
空气在流动过程的沿程压力损失,采用范宁公式计算：
$\Delta {P_{{\rm{pass,}}m,i}} = {\eta _{m,i}}\frac{{{l_{m,i}}}}{{2{d_{m,i}}}}{\rho _{{\rm{air}}}}u_{m,i}^2$ (3)
其中：摩擦系数η与流动有关,取值参考文献[11];m表示进口in、出口out以及通道ch。
在电池端部和导流板之间的区域,局部压力损失为：
$\Delta {P_{{\rm{local,in}},i}} = \frac{{{\xi _{{\rm{in}},i}}}}{2}{\rho _{{\rm{air}}}}u_{{\rm{in}},i - 1}^2$ (4)
$\Delta {P_{{\rm{local,out}},i}} = \frac{{{\xi _{{\rm{out}},i}}}}{2}{\rho _{{\rm{air}}}}u_{{\rm{out}},i + 1}^2$ (5)
其中：ξ为局部阻力系数。
在各电池（或电池与壁面）之间的间隙通道中,局部压力损失主要包括进入通道以及流出通道的局部损失：
$\Delta {P_{{\rm{local}},i}} = \frac{{{\xi _{{\rm{in}} - {\rm{ch,}}i}}}}{2}{\rho _{{\rm{air}}}}u_{{\rm{in}},i}^2 + \frac{{{\xi _{{\rm{ch}} - {\rm{out}},i}}}}{2}{\rho _{{\rm{air}}}}u_{{\rm{out,}}i}^2$ (6)
局部阻力系数与流动状态、几何结构有关。在中间的间隙通道中类似于T形结构,可以得到局部阻力系数随主管和支管的截面比例系数$\psi$、支管和主管的流量比q的变化关系[12]：
${\xi _{{\rm{in}},i}} = q_{{\rm{in,}}i}^2 - \frac{3}{2}{q_{{\rm{in}},i}} + \frac{1}{2}$ (7)
${\xi _{{\rm{out}},i}} = 1 - q_{{\rm{out}},i}^2$ (8)
${\xi _{{\rm{in - ch,}}i}} = q_{{\rm{in - ch}},i}^2\psi _{{\rm{in}},i}^2 - 2\cos \left( {\frac{3}{8}{\rm{\pi }}} \right){q_{{\rm{in - ch}},i}}{\psi _{{\rm{in}},i}} + 1$ (9)
${\xi _{{\rm{ch - out}},i}} = q_{{\rm{ch - out,}}i}^2\psi _{{\rm{out}},i}^2 + 2q_{{\rm{ch - out}},i}^2 - 1$ (10)
由质量守恒方程,在T形结构的出入口处,有：
${u_{{\rm{in}},i}}{A_{{\rm{in}},i}} = {u_{{\rm{in,}}i + 1}}{A_{{\rm{in}},i + 1}} + {u_{{\rm{ch}},i}}{A_{{\rm{in,}}i}}$ (11)
${u_{{\rm{out}},i}}{A_{{\rm{in,}}i + 1}} = {u_{{\rm{out}},i}}{A_{{\rm{out}},i}} + {u_{{\rm{ch,}}i + 1}}{A_{{\rm{out}},i + 1}}$ (12)
其中：A为空气在各部分的流通截面积。
联立求解以上方程组,一旦电池模组的入口总流量确定,整个空气流动阻力网络模型可以求解,空气速度场的分布也可以获得。
1.2 热力学模型
采用空气阻力网络模型可以快速求出电池模组的优化结构,热学模型则求解特定结构下的传热与流动特性。
电池模组内软包电池的温度变化符合能量守恒定律：
${\rho _{\rm{b}}}{c_{p,{\rm{b}}}}\frac{{\partial T}}{{\partial t}} = {\lambda _{\rm{b}}}{\nabla ^2}T + {q_{{\rm{air}}}} + {q_{{\rm{gen}}}}$ (13)
${q_{{\rm{air}}}} = {c_p}m\Delta T = {c_p}\rho u{A_{{\rm{in}}}}\left( {{T_{{\rm{out}}}} + {T_{{\rm{in}}}}} \right)$ (14)
其中：Tin和Tout分别为电池模组内空气的入口温度和出口温度;Ain为电池模组空气入口的面积;u为空气的流速。为获得空气的流速与温度参数,需要对空气域进行仿真计算。
空气流动过程中不断冷却电池模组,其中空气的流动传热要遵循能量守恒方程、动量守恒方程和连续性方程。
$\frac{{\partial T}}{{\partial t}} + \overrightarrow v \cdot \nabla T = \frac{\lambda }{{\rho {c_p}}}{\nabla ^2}T$ (15)
$\frac{{\partial \overrightarrow v }}{{\partial t}} + (\overrightarrow v \cdot \nabla )\overrightarrow v = \overrightarrow f - \frac{1}{\rho }\nabla P + \mu {\nabla ^2}\overrightarrow v$ (16)
$\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \overrightarrow v } \right) = 0$ (17)
其中：ρ、cp、λ和μ分别代表流动空气的密度、比热、热导率和黏度;P为空气压力。
对于整个电池模组的流动与热边界条件设置,具体如下：①入口速度、温度皆恒定,为输入条件;②出口表压力为0;③模组壁面假设为绝热面。
数值计算采用非稳态模型进行求解,时间步长为0.05,收敛的条件是变量残差值低于1.00 × 10-6。经过多次计算,当网格数超过107量级时,电池模组和空气的换热量变化不大,因此采用网格数目为1.01 × 107,计算总耗时约2 h。经过计算,可以获得特定结构下电池模组的温度场以及流场分布。
2 结果与讨论
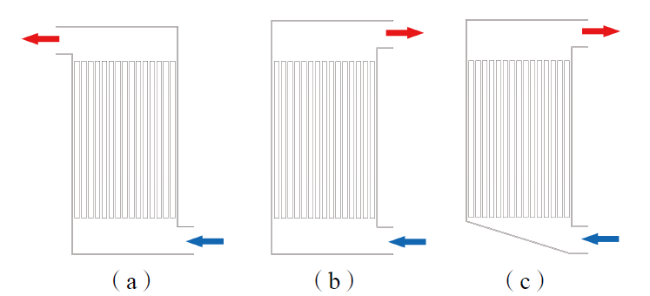
2.1 空气流动阻力网格模型优化结构与对比验证
以各个流道内空气流速的方差为评价指标,利用空气流动阻力网络模型计算不同结构参数下流动特性发现,“Z”字形电池模组的最优结构是w1 = 0 cm、w2 = 0 cm,即进出口导流板倾斜角为0°,如图2a所示。这意味着,调节导流板倾斜角只会增加电池模组内冷却流道空气流速的不均匀性。此时“Z”字形结构的方差为2.58。由于方差较大,因此进一步调整出口方向,变为“C”字形,如图2b所示。以此为基础继续优化上下导流板的角度,发现最优方案是w1 = 4.6 cm、w2 = 0 cm,即入口导流板的倾斜角度为16.7°、出口导流板的倾斜角为0°。图2中三种结构的方差分别是2.58、1.12和0.97。这表明“C”字形结构更利于模组内空气的均匀分配,且优化后的“C”字形结构中空气流量的分配更加均匀。
Fig. 2 Structure schematic of the models: (a) “Z” shape; (b) flat “C” shape; (c) optimized “C” shape图2 模组结构示意图：（a）“Z”字形结构;（b）“C”字形结构;（c）优化的“C”字形结构 |
为验证结论的准确性,采用热力学仿真方法分别对三种结构进行仿真计算,电池模组中不同间隙通道的流速如图3所示。可以发现“Z”字形结构、“C”字形结构以及优化的“C”字形结构三种方案下,“C”字形结构方案的空气流速分布更加均匀,而且经过优化后的“C”字形结构方案的气流流速分布也有所改善。结论与空气流动阻力网格模型的计算结果相同。可以认为经过空气流动阻力网格模型获得的优化结果具有一定的准确性。
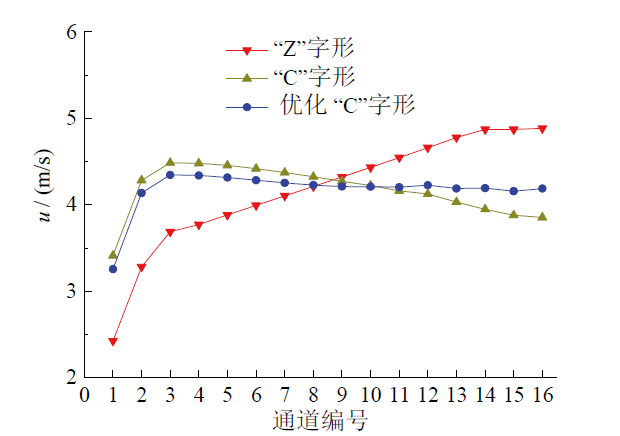
Fig. 3 Velocity in different path of the battery module图3 电池模组中不同间隙通道的流速 |
2.2 不同结构电池模组的流场
由图3可知,不同的流道结构,其流速分布各不相同。其中靠近空气入口端为1号间隙通道,靠近出口端为16号间隙通道（电池间）。在“Z”字形结构中,流道内的空气速度沿着空气入口的方向增大。其中1号间隙通道的空气流速比较小,且小于2.5 m/s,而3 ~ 14号间隙通道内空气流速均匀增加,16通道内空气几乎是1号通道内空气流速的两倍。这显示出“Z”字形结构的流场不均匀性。空气流动当中,压差变化是导致流速差异的主要原因。在“Z”字形结构中,经过每一个通道的空气所流过的路径轨迹的长度基本相同,这意味着沿程阻力比较相似。但是由于入口段的流速较大,静压较小,而且间隙流道垂直于水平入口方向,因此1号通道的流速较小。沿着入口方向,由于受到模组后壁的影响,入口的气流逐渐向通道的方向倾斜,气流有平行于间隙流道的速度分量,因此进入流道内的空气流量逐渐增加。在“C”字形结构中,间隙流道中的流速是沿着入口方向（编号变大的方向）先增大后减小。1号流道内的空气速度最小,为3.4 m/s;3号流道内空气流速最大,为4.49 m/s;3 ~ 14号流道内空气流速均匀降低。显然,“C”字形结构的速度分布比“Z”字形的速度分布更加均匀,速度一致性有了显著的提高。由于风冷系统中空气流速是导致温度一致性的重要因素,因此“C”字形结构的温度分布也将比“Z”字形结构的温度分布更加均匀。导致空气流速不同的主要原因是,在“C”字形结构中,经过每一个通道的空气所流过的路径轨迹的长度相差较大。显然,1号间隙通道的气流流过的路径长度最小,即摩擦损失最小,而远离1号间隙通道的16号间隙通道的内部空气流过的路径最长,摩擦损失较大。路径长短不同引起的压力损失的差异平衡了空气在不同冷却通道内的流量分布。在初始“C”字形结构中,由于模组左下端后壁的影响,空气流速较小。增加入口导流板的角度,有助于降低空气的总压降,提升远端通道的空气流速,从而降低整个模组的流速平方差,增加空气流动的均匀性。对于优化的“C”字形结构,空气流速沿着入口方向（编号变大的方向）先增大后基本保持不变。
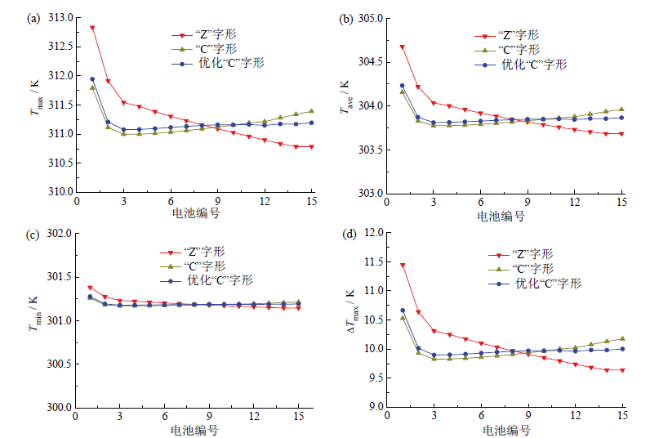
2.3 不同结构电池模组温度场分布
空气流动阻力网格模型求解比较快速,结合智能算法如遗传算法[15]可以获得较好的优化结果。但是该模型不能获得温度场分布,因此采用热力学模型模拟计算电池模组的温度场变化,并验证空气流动阻力网格模型的正确性。假设模型不同冷却结构中的电池组都采用2 C的倍率进行放电,即热源相同。在放电结束后,不同结构电池模组的温度分布情况如图4所示。可以看到“Z”字形的温度变化最大,而“C”字形结构中,电池模组的温度变化较小,而且优化后的“C”字形结构的温度分布最均匀。可以发现,采用热力学模型仿真计算的模组温度结果与采用空气流动阻力网格模型得到的结果一致。可知对于类似结构的模组结构,可以采用空气流动阻力网格模型进行优化。
Fig. 4 The maximum temperature Tmax (a), average temperature Tave (b), minimum temperature Tmin (c) and maximum temperature difference ΔTmax (d) of each battery in the module图4 电池模组内各电池单体的最高温度Tmax（a）、平均温度Tave（b）、最低温度Tmin（c）和最大温差ΔTmax（d） |
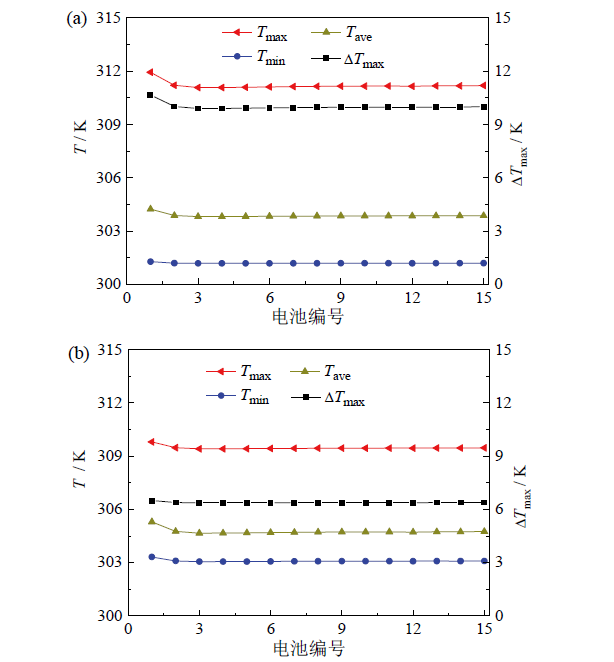
2.4 空气流动方向对冷却效果的影响
由于软包锂离子电池充放电过程中各区域的产热量不同,靠近极耳附近的区域产热量大、温度高,而远离极耳的区域产热量相对较小[13]。因此,以优化后的“C”字形电池模组结构为研究对象,计算空气流动方向改变后的温度分布,结果如图5所示。空气从上端进入时,空气的温度较低,极耳附近区域得到优先冷却。而自下而上的冷却气流方案（方案A）中,空气在流动过程中逐渐升温,达到极耳附近时温度较高,导致极耳的冷却效果不佳,整体的温度均匀性差。相比于下进上出的方案（方案A）,上进下出的方案（方案B）的最高温度和最大温差都有明显的下降,分别下降了约2℃和3℃。另外,在方案B中,空气流到底部时,空气温度相对方案A中的空气温度要高,因此底部的换热效果较差,因而方案B中的最低温度比方案A中的最低温度要高。这也使得方案B中的电池模组的温度更加均匀,保证电池的一致性,有利于长期的运行。另一方面,相对于下进上出的流动方式,空气上进下出冷却电池时,单体电池的平均温度略有上升。这表明空气与电池总的换热量有所下降。
Fig. 5 Cooling of battery module with different air flow direction图5 不同空气流动方向时模组内各电池单体的冷却效果：（a）空气下进上出（方案A）;（b）空气上进下出（方案B） |
结果显示,将模组的空气入口布置在上方,出口布置在下方,采用空气上进下出的流动方式可进一步降低模组内单体电池的最高温度,提升单体电池温度场的一致性。