开放科学（资源服务）标识码（OSID）
0 引言
在纳米碳酸钙的生产工艺中,热风炉是其中的一个重要设备,用于产生热风烘干碳酸钙。在传统工艺中,热风炉多采用普通圆管空气预热器,设备体积庞大,钢材耗用量大,而且换热效率低。而以椭圆扭曲管为换热元件的空气预热器（椭圆扭曲管空气预热器）体积小,换热效率高,能够提高烟气余热利用率以降低燃料消耗量,适合在纳米碳酸钙行业中推广应用。
椭圆扭曲管是一种高效强化传热的换热管,MUSHABBAB[1]对椭圆扭曲管换热器壳程的污垢特性进行了试验研究,为椭圆扭曲管换热器在工业上的应用提供了数据基础。张杏祥等[2]发现在高普朗特数和低雷诺数下椭圆扭曲管强化传热效果较为明显,并拟合了相关的准则公式。GU等[3]通过实验研究发现椭圆扭曲管的传热系数会受到管子结构参数的影响,与圆管相比可提高1.5 ~ 3倍。YAN等[4]通过实验研究发现椭圆扭曲管有利于提高高黏度流体的传热性能,且相对于扭曲比,长短轴比对换热性能与压降性能的影响更大。WU等[5]通过数值模拟发现,与椭圆管相比,纳米流体在椭圆扭曲管中产生的旋转运动有利于提高传热性能,且平均努塞尔数和压降随着雷诺数和纳米粒子体积浓度的增加均增加,而随螺距的增加而减小。黄军[6]通过FLUENT软件对椭圆扭曲管内的碰撞磨蚀情况进行模拟研究,获得了不同操作参数下椭圆扭曲管内流态化粒子对管壁的平均磨蚀率,分析了影响平均磨蚀率的主次因素。马芳芳等[7]基于场协同原理对椭圆扭曲管进行分析,发现长短轴比的增大促进了管内流体的速度场与温度场的协同性从而利于提高换热性能,但削弱了速度场与压力场的协同性从而提高了设备的能耗。CHENG等[8]对椭圆扭曲管内的低雷诺数流体进行研究,考察了雷诺数、长短轴比及螺距对综合性能评价因子的影响。
本文在对椭圆扭曲管介绍的基础上,在相同雷诺数下分别对圆管和椭圆扭曲管进行数值模拟,通过对管内流场的分析来揭示椭圆扭曲管的强化传热特性,并对实际的工程案例进行研究,探讨椭圆扭曲管空气预热器的节材节能效果,以期优化纳米碳酸钙生产设备,进一步降低排烟温度,提高生产过程的燃料利用率,从而降低生产成本,达到节能节材的效果。
1 椭圆扭曲管强化传热机理
椭圆扭曲管可由普通光滑圆管冷轧扭曲加工而成,其横截面呈椭圆形,主要几何参数包括基圆管外径do、管壁厚δ、外椭圆管长轴A、外椭圆管短轴B及螺距P。椭圆扭曲管在加工过程中两端保留圆形,便于与管板装配,椭圆扭曲管的结构示意图如图1a所示。本研究选用的椭圆扭曲管由do为32 mm的圆管压扁扭曲而成,其中长轴A = 38 mm、短轴B = 31 mm、螺距P = 300 mm。
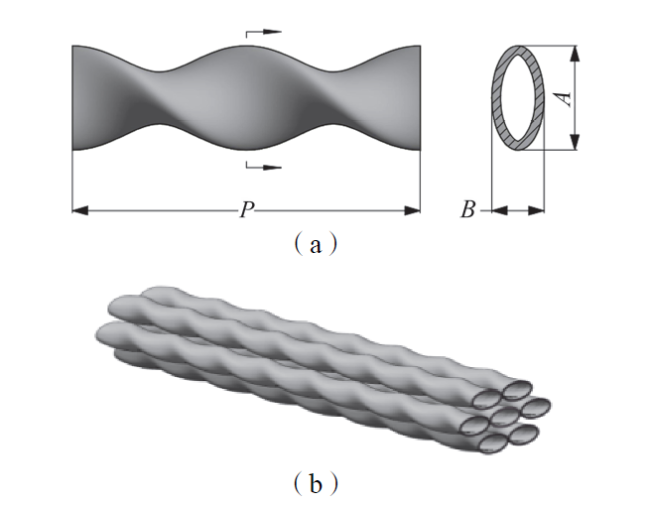
Fig. 1 Twisted oval tube structure (a); self-supporting twisted oval tube (b)图1 椭圆扭曲管结构（a）;椭圆扭曲管自支撑示意图（b） |
2 计算模型
2.1 数学模型及计算方法
在数值计算过程中,湍流模型采用Standard k-ε模型,流体在扭曲椭圆管内流动与换热的控制方程分别计算如下。
质量守恒方程：
$\nabla \cdot \rho U = 0$ (1)
动量守恒方程：
$\rho U \cdot \nabla U = - \nabla p + \mu {\nabla ^2}U$ (2)
能量守恒方程：
$\nabla \cdot \left( {\rho U{C_p}T} \right) = \nabla \cdot \left( {\lambda \nabla T} \right)$ (3)
式中：ρ、U、μ分别为空气的密度、流速、动力黏度。
湍动能方程：
$\begin{array}{c}\rho \frac{{\partial k}}{{\partial t}} + \rho \frac{{\partial \left( {k{u_i}} \right)}}{{\partial {x_i}}}{\rm{ = }}\frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + \mu t\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} + \rho \varepsilon \end{array}$ (4)
湍流耗散率方程：
$\begin{align} & \rho \frac{\partial \varepsilon }{\partial t}+\rho \frac{\partial \left( \varepsilon {{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left( {{\alpha }_{\varepsilon }}{{\mu }_{\text{eff}}}\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right)+ \\ & {{\mu }_{\text{t}}}\frac{\varepsilon }{k}\left[ {{C}_{1\varepsilon }}-\frac{\eta \left( 1-{\eta }/{{{\eta }_{0}}}\; \right)}{1+\beta {{\eta }^{3}}} \right]\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)\frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}-\rho {{C}_{2\varepsilon }}\frac{{{\varepsilon }^{2}}}{k} \\ \end{align}$ (5)
式中：μt、μeff和η的定义如下：
${\mu _{\rm{t}}} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }$ (6)
${\mu _{{\rm{eff}}}} = {\mu _{\rm{t}}} + \mu$ (7)
$\eta = s\frac{k}{\varepsilon }$ (8)
其中,s为应变张量模数的平均值。
式（5）及式（6）中选用的方程模型系数值分别为Cμ = 0.084 5、αk = αε = 1.39、C1ε = 1.42、C2ε = 1.68、η0 = 4.377、β = 0.012。
在数值计算过程中控制方程的离散采用二阶迎风格式,壁面采用标准壁面函数法进行处理,压力-速度耦合采用SIMPLE方式。计算过程采用的边界条件为：壁面边界条件Tw = 350 K;进口边界条件为进口流速 = 13 m/s、kin = 常数、εin = 常数、Tin = 300 K。数值研究中认为空气物性不变,具体物性参数如下：μ = 1.789 4 × 10-5 N⋅s/m2,Cp = 1 006.43 J/(kg⋅K),λ = 0.024 2 W/(m⋅K),ρ = 1.225 kg/m3。
2.2 网格划分及无关性验证
对三维模型进行结构化网格划分,为实现对壁面附近边界层流体的准确捕捉以保证计算结果的精确性,对近壁区域进行加密,图2是结构化网格的示意图。
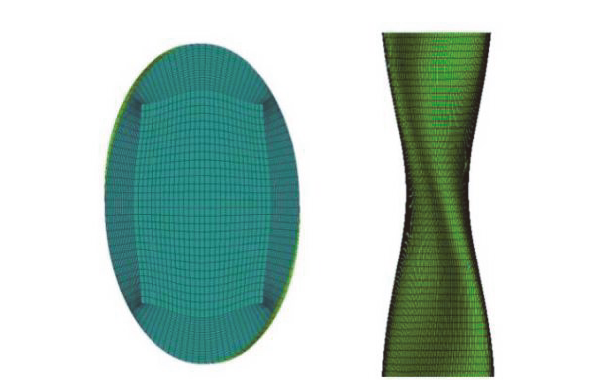
Fig. 2 Structured grid diagram图2 结构化网格示意图 |
对模型进行数值计算之前需对网格的无关性进行验证,在保证计算精度的条件下尽量减少计算时间。对近壁处的网格进行不同程度的加密,得到的网格数量分别为90万、100万、110万、130万和150万,图3显示了不同网格数量下椭圆扭曲管内努塞尔数Nu的变化情况。由图中可以看出,当网格数量从130万变化到150万时,努塞尔数从68.2变化到了68.7,仅增长了0.7%,因此选用的计算网格数量为130万。
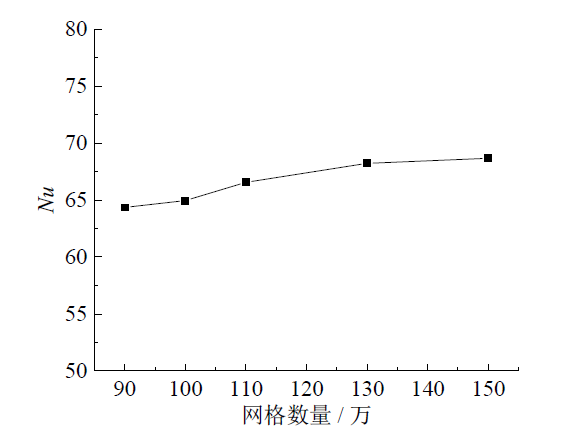
Fig. 3 Nu changes with the number of grid图3 努塞尔数随网格数量的变化 |
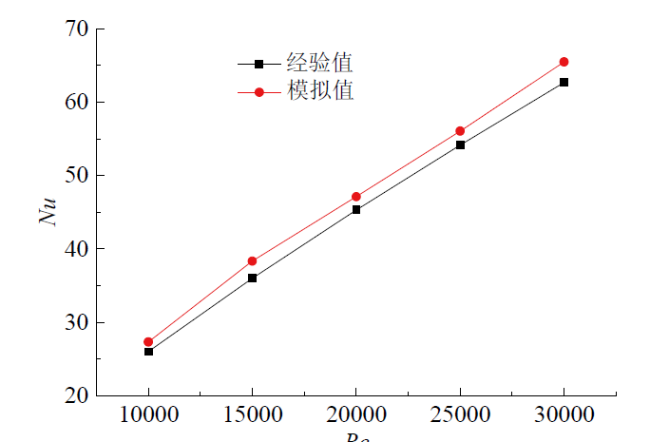
2.3 模拟结果准确性验证
3 结果与分析
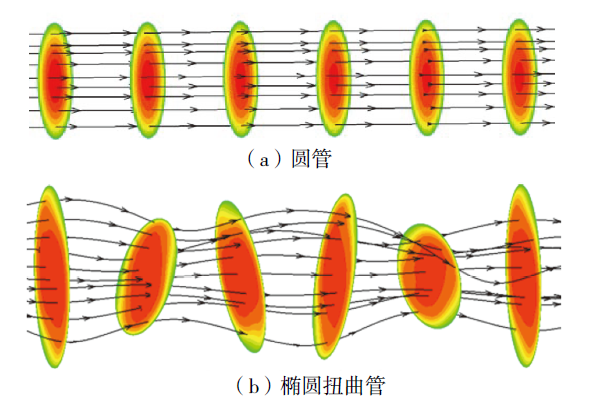
Fig. 5 Inside velocity distribution of the tube图5 管内速度分布图 |
图6为换热管内流体温度沿管长方向的变化情况。
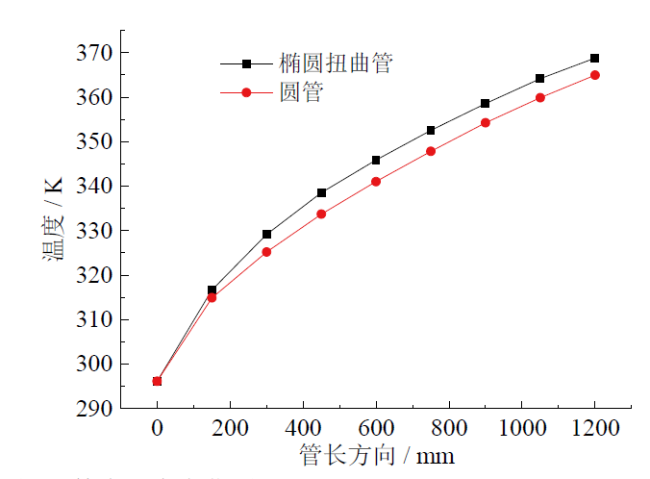
Fig. 6 Inside temperature distribution of the tube图6 管内温度变化图 |
从图6中可以看出,沿着工质流动的方向,工质吸收从管壁传来的热量,温度逐渐上升,但温度的变化率逐渐降低,说明流体吸收的热量越来越少。这主要是由于空气进入管子与管壁热交换时,有入口段的存在,入口段的热边界层较薄,局部表面传热系数比充分发展段的高,而且工质温度与管壁温差较大,所以吸热速度快;随着空气在管内流动,逐渐进入充分发展段,热边界层厚度逐渐增长并趋于稳定,空气温度逐渐上升,与管壁温差逐渐减小,吸收的热量也逐渐减少。此外,椭圆扭曲管内流体温度始终比圆管的高,说明流体在椭圆扭曲管内升温更快,吸热更多,换热效果更好。
3.1 湍流强度对换热管性能的影响
湍流强度是反映流体湍流运动特性最重要的特征量,等于湍流脉动速度与平均速度的比值,反映了脉动速度的相对强度。图7是流体湍流强度沿管长方向的变化情况,从图中可以看出椭圆扭曲管和圆管的湍流强度沿管长方向变化趋势一致,沿管长方向0 ~ 600 mm范围内,湍流强度逐渐增大,600 mm之后基本趋于稳定。椭圆扭曲管的湍流强度始终比圆管的高,说明在椭圆扭曲管内流体所受到的扰动更为强烈,从而有利于破坏流体边界层,提高流体的传热效率。在椭圆扭曲管内湍流强度的平均值为0.107,比圆管的高24%。
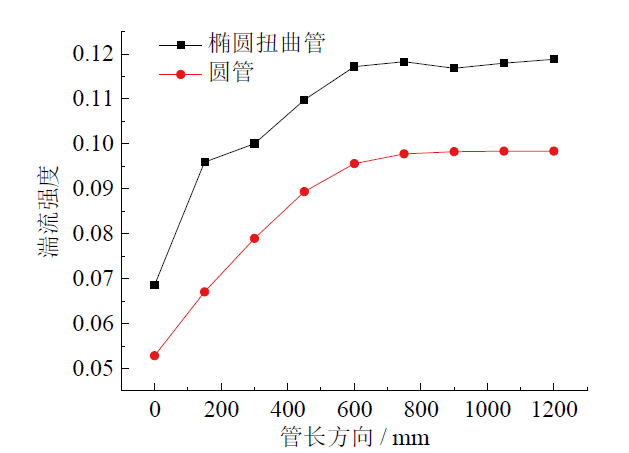
Fig. 7 Inside turbulence intensity distribution of the tube图7 管内湍流强度变化图 |
3.2 流体速度与温度梯度的协同角对换热管性能的影响
换热管的传热性能与速度和温度梯度之间的协同角有关,其协同角的表达式为[13]：
$\theta=arccos \frac{\vec u ・ (-\vec{\nabla T})}{|\vec u||-\vec{\nabla T}|}$ (9)
式中：$\vec u$为速度矢量;$\vec{\nabla T}$为温度梯度矢量。当协同角越小时,流体的速度场与温度场协同性越好,越有利于热量的传递和换热效果的提升[13]。
图8是流体速度与温度梯度协同角沿管长方向的变化情况,从图中可以发现圆管与椭圆扭曲管的速度与温度梯度协同角沿管长方向变化趋势基本一致,协同角在100 ~ 300 mm范围内急剧增大,在300 ~ 500 mm范围内增幅减小,而在500 mm之后有所下降。此外,在椭圆扭曲管内协同角始终比圆管的小,说明椭圆扭曲管内流体的速度场与温度场协同性优于圆管,更加利于热量的传递和换热效果的提升。在椭圆扭曲管内协同角的平均值为88.8°,比圆管低0.2°。
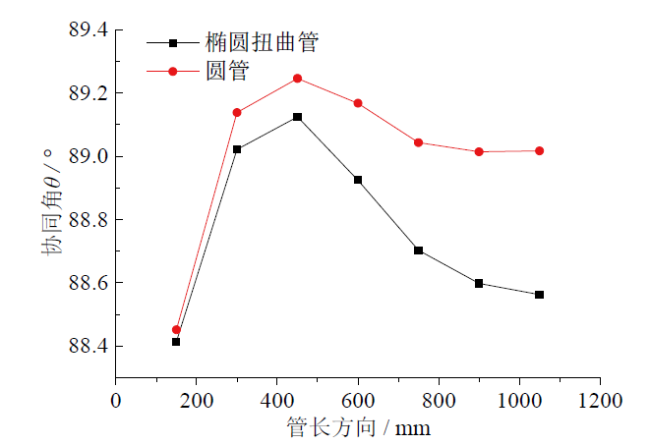
Fig. 8 Coordinate angle θ along the tube length direction图8 沿管长方向协同角θ变化图 |
3.3 流体速度及压力梯度的协同角对换热管性能的影响
换热管的阻力性能与流体速度和压力梯度之间的协同角有关,其协同角的表达式为[14]：
$J=arccos \frac{\vec u ・ (-\vec{\nabla P})}{|\vec u||-\vec{\nabla P}|}$ (10)
式中：$\vec{\nabla P}$为压力梯度矢量。当协同角越小时,流体的速度场与压力场协同性越好,越有利于降低流体的流动阻力[14]。
图9是流体速度与压力梯度协同角沿管长方向的变化情况,从图中可以发现换热管内速度与压力梯度之间的协同角基本处于稳定状态,但椭圆扭曲管的速度与压力梯度之间的协同角大于圆管,平均值约为61.7°,高于光滑圆管约60°。与圆管相比,椭圆扭曲管换热效果提升的同时会导致流动阻力的增大。
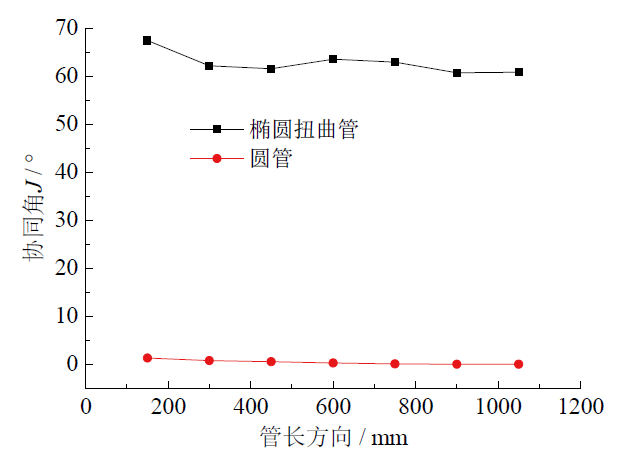
Fig. 9 Coordinate angle J along the tube length direction图9 沿管长方向协同角J变化图 |
3.4 椭圆扭曲管强化传热的综合评价
根据场协同的分析,椭圆扭曲管在强化的同时,导致了阻力的增大,即导致系统功耗的增加,这种强化从能量上是否经济,可以用综合评价因子进行评价：
$\xi {\rm{ = }}\frac{{Nu/N{u_0}}}{{{{\left( {f/{f_0}} \right)}^{1/3}}}}$ (11)
式中：Nu和f为椭圆扭曲管的努塞尔数和流动阻力系数,Nu0和f0为圆管的努塞尔数和流动阻力系数;当ξ > 1时,说明在同样的输送功率下椭圆扭曲管输出热量大于圆管,强化传热的效果是可取的,反之则不经济。圆管的传热与阻力经验公式[15]已经非常成熟,即：
$Nu{\rm{ = }}0.023R{e^{0.8}}P{r^{0.4}}$ (12)
$f{\rm{ = }}0.3164/R{e^{0.25}}$ (13)
其中：Re = 1 × 104 ~ 1.2 × 105;Pr = 0.7 ~ 120;l/d ≥ 60。
$Nu{\rm{ = }}0.023R{e^{0.8251}}{\left( {A/B} \right)^{0.3736}}{\left( {P/{d_{\rm{e}}}} \right)^{0.1617}}P{r^{1/3}}$ (14)
$f{\rm{ = }}15.292R{e^{ - 0.471}}{\left( {A/B} \right)^{0.471}}{\left( {P/{d_{\rm{e}}}} \right)^{0.409}}$ (15)
其中：1 × 103 < Re < 1 × 104;11.49 < P/de <19.84;1.65 < A/B < 3.11;Pr ≈ 0.7。
经计算,本项目综合评价因子为η = 1.13 > 1,说明虽然强化传热伴随阻力增大,但综合效果依然具有良好的经济性。
4 案例分析
4.1 案例描述
某纳米碳酸钙制造厂的热风炉空气预热器改造项目中,计划通过增加一个空气预热器以解决现存的排烟温度高、能源利用率低、煤耗高的问题。分别对椭圆扭曲管空气预热器和光滑圆管空气预热器进行了设计计算,管材采用ND钢,壳体材质为碳钢Q235。椭圆扭曲管空气预热器与传统光滑圆管空气预热器性能参数对比如表1所示,可以发现椭圆扭曲管空气预热器比传统光滑圆管换热面积减少27.9%,体积缩小37%,有利于降低投资成本和节省安装空间。图10是椭圆扭曲管空气预热器现场安装图,增加了椭圆扭曲管空气预热器后,对烟气系统、空气系统和热风炉鼓风系统、给煤系统的运行工况联调,达到了最佳运行工况,通过现场数据的采集证实已达到设计要求。
Table 1 Performance parameters comparison表1 性能参数对比表 |
| 参数 / 单位 | 圆管空气预热器 | 椭圆扭曲管空气预热器 | 对比 |
|---|---|---|---|
| 空气进口温度 / ℃ | 25 | 25 | / |
| 空气出口温度 / ℃ | 120 | 120 | / |
| 空气流量 / (m3/h) | 17 000 | 17 000 | / |
| 烟气进口温度 / ℃ | 130 | 130 | / |
| 烟气出口温度 / ℃ | 95 | 95 | / |
| 烟气流量 / (Nm3/h) | 40 268 | 40 268 | / |
| 换热管尺寸 / mm | Φ 32 × 2 × 5 500 | Φ 322 × 2 × 4 000;A = 38,B = 21,P = 300 | / |
| 管程压降 / Pa | 543 | 786 | +44.80% |
| 壳程压降 / Pa | 487 | 642 | +31.80% |
| 总换热面积 / m2 | 509 | 367 | -27.90% |
| 总传热系数 / (W∙m-2∙K-1) | 36.8 | 47.9 | +30.20% |
| 总体尺寸 / mm | 2 400 × 1 800 × 5 500 | 2 200 × 1 700 × 4 000 | -37.00% |
| 换热管材质 | ND钢 | ND钢 | / |
| 壳体材质 | Q235 | Q235 | / |
| 换热管重量 / t | 8.65 | 6.24 | -27.9% |
| 设备投资（不含安装费）/ 万元 | 3.63 | 2.62 | -27.9% |
注：对比以圆管空气预热器参数量值为基础,即变化量值与圆管空预器量值的百分比。 |
Fig. 10 Installation of air preheater with twisted oval tube图10 椭圆扭曲管空气预热器现场安装图 |
4.2 经济性分析
椭圆扭曲管空气预热器将排烟温度从130℃降低到95℃,回收余热629.70 kJ/s,每年运行时间按8 000 h计算,可回收热量18 135 416 397 kJ/a,折合标煤619.59 t/a,标煤价格按800元/t计算,则可节约49.57万元/a,相当于每月4.13万元。相对于圆管,椭圆扭曲管换热面积减少27.9%,管壁厚度相同的情况下,换热管的重量就相应减少了27.9%,故相较于圆管,节材效果显著。鼓风机功率13 kW,引风机功率22 kW,年运行时间8 000 h,分别增加阻力44.8%和31.8%,共增加能耗1 008 000 000 kJ/a,折合标煤34.44 t,每月0.23万元,可见因阻力引起的能耗增加相对于余热回收的能量非常少,每月净回收热量价值仍有3.9万元,每年仍有46.8万元净值回收。椭圆扭曲管空气预热器设备投资2.62万元,仅需一个月就可以回收设备成本,设备寿命可达5 ~ 10年,余热回收效益可观。
5 结论
分别对椭圆扭曲管和圆管进行数值模拟,对比分析管内流场的流动特性,并对实际的工程案例进行研究,结论如下：
（1）相对于圆管,椭圆扭曲管更有利于增加流体的湍动性,从而强化传热,提高流体的换热效率。
（2）相对于圆管,椭圆扭曲管内流体的速度场与温度场的协同性更好,而速度场与压力场的协同性更差。虽然强化传热导致阻力增大,但是并不影响余热回收带来的经济效益。
（3）相对于传统的圆管空气预热器,椭圆扭曲管空气预热器可减少换热面积27.9%,缩小体积37%,节能节材效果以及经济效益显著。为包括其他行业在内的传统圆管空气预热器的性能优化提供了参考依据。
符号表
d—基圆管直径,m
de—当量直径,m
l—长度,m
δ—管壁厚,m
P—扭矩,m
A—椭圆扭曲管横截面外长轴,m
B—椭圆扭曲管横截面外短轴,m
Re—雷诺数
Pr—普朗特数
Nu—努塞尔数
u—速度,m/s
μ—运动黏度,Pa∙s
μt—湍流粘性系数,Pa∙s
μeff—有效粘性系数,Pa∙s
ε—耗散率
η—表征小尺度运动的长度尺度
ρ—密度,kg/m3
k—湍动能,J
i,j—计算网格方向
λ—阻力系数
ξ—综合评价因子