0 引言
目前,基于核能的空间能量转换系统分为静态和动态能量转换系统[4],动态能量转换系统相比于静态能量转换系统具有更高的系统效率,因此,空间核能和动态能量转换系统的结合成为空间电源技术的理想方案之一。动态能量转换系统包括斯特林循环、朗肯循环和布雷顿循环系统。基于布雷顿循环的空间能量系统具有效率高、单位辐射散热面积对应的系统功率大等特点[5,6],因此,研究人员针对该系统开展了大量研究。RIBEIRO等[5]针对空间核能布雷顿循环系统建立了基于设计的稳态模型,研究了换热器的热导率、压气机效率和辐射散热器的面积等系统组件参数对系统效率的影响规律,结果表明,上述系统组件参数的增大均有利于提高系统的效率,且辐射散热面积的增大对系统效率的影响最大。TORO等[6]研究了采用H2、N2和两者的混合物作为循环工质对空间布雷顿循环系统热效率的影响,结果表明,采用N2作为循环工质可获得最高的系统热效率。杨谢等[7]从绝热系数和相对压损系数等角度研究了氦-氙混合气体成分配比的变化对空间布雷顿循环系统效率的影响规律,结果表明,气体绝热系数的变化对系统效率影响较小,提高混合气体中氙气的比例会增加相对压损系数,进而降低系统效率。GALLO等[8]针对空间核能布雷顿循环的压气机和涡轮建立了设计和分析模型,并对系统开展性能分析,结果表明系统在设计工况下可实现的最高热效率为26%。ROMANO等[9]针对辐射散热系统中热管的工作温度和材料开展了研究,当系统输入热功率为157 kW、热源温度为1 150 K时,热管的最佳工作温度范围为450 ~ 500 K,且选用金属钛作为热管的结构材料。
相比于地面的能量转换系统,空间能量系统不仅要考虑系统的效率,系统的质量也是影响系统方案可行性和发射成本的重要因素。因此,相同输出功率的前提下,更轻的系统质量成为系统方案可行性的重要评估指标[10]。
为了综合评估系统的效率和质量等性能,本文以“质量比功率”（质量比功率表示单位输出电功率下的系统质量）为评价指标,对空间核能布雷顿循环系统进行参数分析,研究关键循环参数和关键部件性能参数对系统性能的影响规律。同时采用正交实验法进行参数优化,为空间核能布雷顿循环系统的设计和优化提供一定的参考。
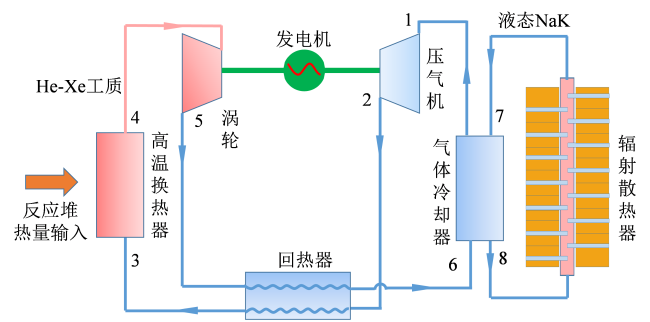
1 空间核能布雷顿循环系统描述
空间核能布雷顿循环系统的示意图如图1所示,图2为布雷顿循环的T-S图。系统运行时,反应堆作为系统的热源,低温的外太空作为系统的冷源。工质首先经过压气机压缩（过程1→2）,压气机出口的高压气体经过回热器与涡轮出口的高温气体进行换热升温（过程2→3）。回热器预热后工质经过高温换热器换热进一步升温（过程3→4）。然后,高温、高压的循环工质进入涡轮膨胀做功（过程4→5）,其中一部分功用于驱动压气机转动压缩工质,一部分功通过发电机转换成电能（涡轮、压气机和发电机安装在同一转轴上）。涡轮出口的工质经过回热器换热降温后（过程5→6）,在气体冷却器与辐射散热器的液态钠钾合金（NaK）进行热交换（过程6→1）,从而将废热传递给辐射散热器,其中废热以热辐射的形式排放至外太空。之后工质返回压气机,完成闭式循环。
Fig. 1 Schematic diagram of the space nuclear Brayton cycle图1 空间核能布雷顿循环系统示意图 |
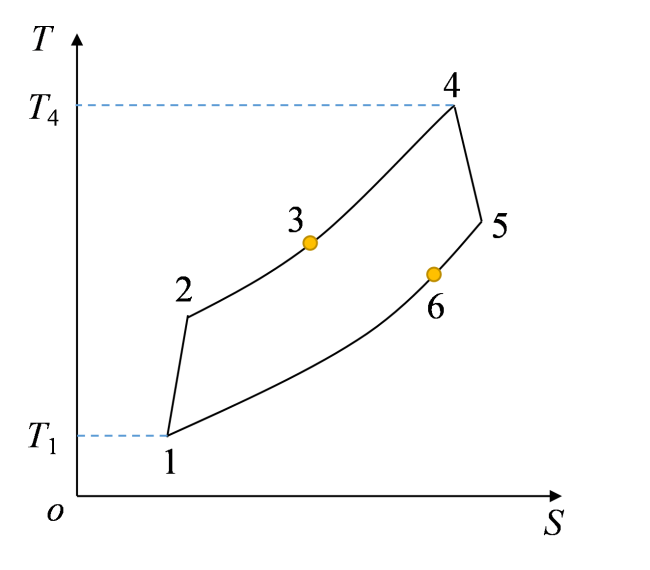
Fig. 2 T-S diagram of the Brayton cycle图2 布雷顿循环T-S图 |
根据EL-GENK等[11]的研究结果,本文采用摩尔质量为40 g/mol的He-Xe（氦气和氙气）混合气体作为布雷顿循环的工质,氦气和氙气对应的摩尔分数分别为72%和28%。
2 空间核能布雷顿循环数学模型
2.1 循环组件数学模型
循环工质在压气机中被压缩,温度和压力升高。根据文献[12],压气机进出口温度和压力满足以下关系：
$\left( \frac{{{T}_{\text{2}}}}{{{T}_{1}}} \right)={{\left( \frac{{{P}_{2}}}{{{P}_{1}}} \right)}^{{\left( \gamma -1 \right)}/{\left( {{\eta }_{\text{C}}}\gamma \right)}\;}}$ (1)
式中：ηC为压气机效率;γ为工质的比热比。
则压气机耗功
${{W}_{\text{C}}}=G{{\overline{C}}_{P,1\to 2}}\left( {{T}_{2}}-{{T}_{1}} \right)$ (2)
式中：G为循环工质的质量流量;${{\overline{C}}_{P,1\to 2}}$为过程1→2的平均定压比热,且${{\overline{C}}_{P,1\to 2}}={\left( {{C}_{P,1}}+{{C}_{P,2}} \right)}/{2}\;$,下文同理。
工质在涡轮膨胀过程时,工质进出口温度和压力满足以下关系：
$\left( \frac{{{T}_{5}}}{{{T}_{4}}} \right)={{\left( \frac{{{P}_{4}}}{{{P}_{5}}} \right)}^{{{\eta }_{\text{T}}}{\left( 1-\gamma \right)}/{\gamma }\;}}$ (3)
式中：ηT为涡轮效率。
则涡轮膨胀做功
${{W}_{\text{T}}}=G{{\overline{C}}_{P,4\to 5}}\left( {{T}_{4}}-{{T}_{5}} \right)$ (4)
对于回热器的换热过程,压气机出口的工质经过程2→3进行预热升温,涡轮出口的高温工质经过程5→6释放余热,提高循环效率。回热器热交换过程满足以下能量平衡方程：
$G{{\overline{C}}_{P,2\to 3}}\left( {{T}_{3}}-{{T}_{2}} \right)=G{{\overline{C}}_{P,5\to 6}}\left( {{T}_{5}}-{{T}_{6}} \right)$ (5)
对于回热器,回热度α为实际回热量与最大回热量的比值
$\alpha \text{=}\frac{G{{\overline{C}}_{P,2\to 3}}\left( {{T}_{3}}-{{T}_{2}} \right)}{G\left( {{C}_{P,5}}{{T}_{5}}-{{C}_{P,2}}{{T}_{2}} \right)}$ (6)
辐射散热器主要由一定数量的热管组成。空间布雷顿循环的废热由热管冷凝段的翅片以热辐射的形式排放至外太空。辐射传热方程如下：
${{Q}_{\text{rad}}}\text{=}\sigma N{{A}_{\text{hp}}}\varepsilon \left( T_{\text{c}}^{4}-T_{\text{sp}}^{4} \right)$ (7)
式中：σ为斯蒂芬-波尔兹曼常数;N为热管的数量;Ahp为单根热管的辐射散热面积;ε为辐射发射率,取0.9;Tsp为冷源温度,取200 K;Tc为热管冷凝段温度。
2.2 布雷顿循环性能计算
循环的输出功为涡轮膨胀功和压气机压缩功之差：
$W={{W}_{\text{T}}}-{{W}_{\text{C}}}$ (8)
热源输入的热量为：
${{Q}_{\text{in}}}=G{{\overline{C}}_{P,3\to 4}}\left( {{T}_{4}}-{{T}_{3}} \right)$ (9)
在进行方案设计时,热源输入热量为5 100 kW。
辐射散热器的散热量为：
${{Q}_{\text{rad}}}=G{{\overline{C}}_{P,6\to 1}}\left( {{T}_{6}}-{{T}_{1}} \right)$ (10)
循环发电量为：
$P=\left( {{W}_{\text{T}}}-{{W}_{\text{C}}} \right){{\eta }_{\text{M}}}{{\eta }_{\text{G}}}$ (11)
式中：ηM为机械效率;ηG为发电机效率。
循环发电效率为发电量与热源输入热量的比值：
${{\eta }_{\text{e}}}\text{=}\frac{\left( {{W}_{\text{T}}}-{{W}_{\text{C}}} \right){{\eta }_{\text{M}}}{{\eta }_{\text{G}}}}{{{Q}_{\text{in}}}}$ (12)
3 系统组件质量评估
由于空间核能布雷顿循环系统紧凑,管道和辅助部件的质量相对恒定,而且质量比系统主要组件的质量小得多。因此,在进行质量评估时,管道和辅助部件的质量忽略不计[1]。
空间核能布雷顿循环系统的热电转换单元包括压气机、涡轮和安装在同一转轴上的交流发电机,根据文献[13],热电转换单元的质量计算如下：
${{M}_{\text{EC}}}={{\xi }_{\text{EC}}}D_{\text{C}}^{2}$ (13)
${{D}_{\text{C}}}=\frac{\sqrt{{{\overline{C}}_{P,1\to 2}}{\left( {{T}_{2}}-{{T}_{1}} \right)}/{\psi }\;}}{\text{ }\!\!\pi\!\!\text{ }n}$ (14)
式中：${{\xi }_{\text{EC}}}$为热电转换单元的比质量,下文同理;DC为压气机的等效直径;$\psi $为压头系数;n为转轴的转速。
回热器的质量计算如下[14]：
${{M}_{\text{rec}}}={{\xi }_{\text{rec}}}A_{\text{rec}}^{{}}$ (15)
${{A}_{\text{rec}}}=\frac{{{Q}_{\text{rec}}}}{{{h}_{\text{rec}}}\cdot \Delta {{t}_{\text{lm}}}}$ (16)
式中：Arec为回热器的换热面积;Qrec为回热器换热量;hrec为回热器总传热系数;∆tlm为回热器换热的对数平均温差。
高温换热器和气体冷却器的计算方式与回热器类似,计算如下：
${{M}_{\text{hex}}}={{\xi }_{\text{hex}}}A_{\text{hex}}^{{}}$ (17)
${{M}_{\text{gc}}}={{\xi }_{\text{gc}}}A_{\text{gc}}^{{}}$ (18)
辐射散热器的质量估算如下[15]：
${{M}_{\text{rad}}}={{\xi }_{\text{rad}}}A_{\text{rad}}^{{}}$ (19)
$A_{\text{rad}}^{{}}=N{{A}_{\text{hp}}}$ (20)
式中：Arad为总的辐射散热面积;N为热管的数量,主要由辐射散热温度和散热量决定。
忽略管道和辅助部件的质量,系统的总质量为各主要组件的质量之和,计算表达式如下：
${{M}_{\text{s}}}={{M}_{\text{EC}}}+{{M}_{\text{rec}}}\text{+}{{M}_{\text{hex}}}+{{M}_{\text{gc}}}+{{M}_{\text{rad}}}$ (21)
系统的质量比功率定义为单位发电量对应的系统质量,计算表达式如下：
${{S}_{\text{m}}}\text{=}\frac{{{M}_{\text{s}}}}{\left( {{W}_{\text{T}}}-{{W}_{\text{C}}} \right){{\eta }_{\text{M}}}{{\eta }_{\text{G}}}}$ (22)
Table 1 Parameter configuration related to the mass assessment of the system表1 系统质量评估的相关参数配置 |
| 参数 | 含义 | 数值 |
|---|---|---|
| ξEC / (kg/m2) | 热电转换单元的比质量 | 5 360 |
| ξrec / (kg/m2) | 回热器的比质量 | 1.8 |
| ξhex / (kg/m2) | 高温换热器的比质量 | 5.9 |
| ξrad / (kg/m2) | 辐射散热器的比质量 | 6.46 |
| ξgc / (kg/m2) | 气体冷却器的比质量 | 5.9 |
| ψ | 压气机的压头系数 | 0.66 |
| Ahp / m2 | 单根热管的辐射散热面积 | 0.25 |
4 热力学参数分析
对于空间核能布雷顿循环系统而言,影响系统性能的运行参数较多,其中压气机进口温度、压气机压比和涡轮进口温度的变化对循环工质的温度、压力和系统组件的热功转换有着重要的影响,从而影响系统的效率和组件质量的变化。基于上述建立的空间核能布雷顿热力循环模型和系统组件的质量评估方法,研究循环关键参数压气机进口温度、压气机压比和涡轮进口温度对系统热力性能和质量的影响规律。
4.1 压气机进口温度
不同压气机进口温度条件下,压气机的工作状态和循环工质的状态参数都会变化,进而影响系统性能。因此有必要对压气机的进口温度进行分析。
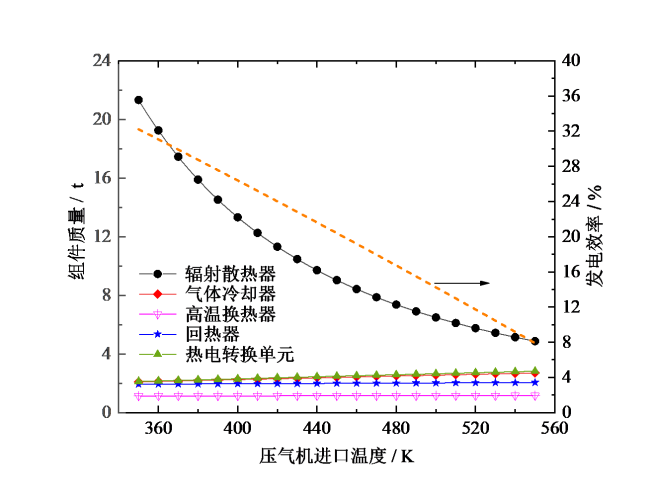
Fig. 3 Variation of the component weight and electrical efficiency at different inlet temperatures of the compressor图3 不同压气机进口温度下组件质量和发电效率的变化 |
上述现象可结合图4进行分析。循环发电效率降低意味着辐射散热量的增加,与此同时,辐射散热器液态NaK工质的温度随着压气机进口温度的升高而不断升高,这有利于增加热管翅片的辐射散热温度,结合黑体辐射定律,辐射散热器的面积与温度的四次方成反比,因此辐射散热器的质量呈下降的趋势。
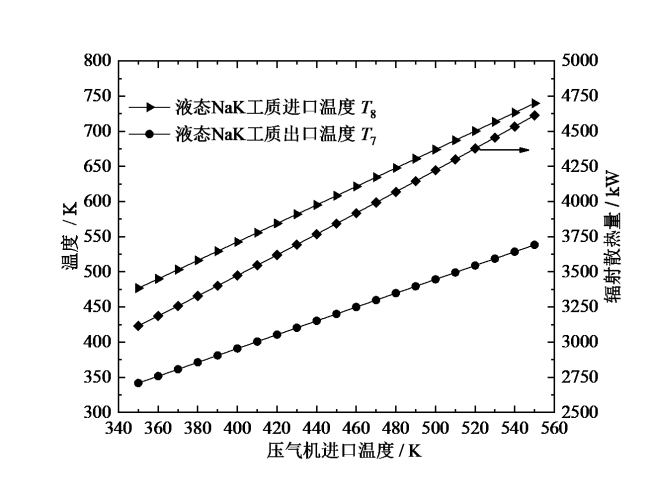
Fig. 4 Variation of the working temperatures and heat dissipation of the radiator at different inlet temperatures of the compressor图4 不同压气机进口温度下辐射散热器的工作温度和散热量的变化 |
系统的总体性能随压气机进口温度的变化如图5所示。随着压气机进口温度的升高,发电量线性下降,而系统质量下降的速率逐渐降低（主要受辐射散热器质量变化的影响）。同时,质量比功率呈现先减小后增大的趋势,当压气机进口温度在410 K时,质量比功率取得最小值,为15.55 kg/kW。因此,在同时考虑质量和电性能进行系统方案设计时,应选择合适的压气机进口温度使系统质量和发电性能之间达到良好的平衡关系。
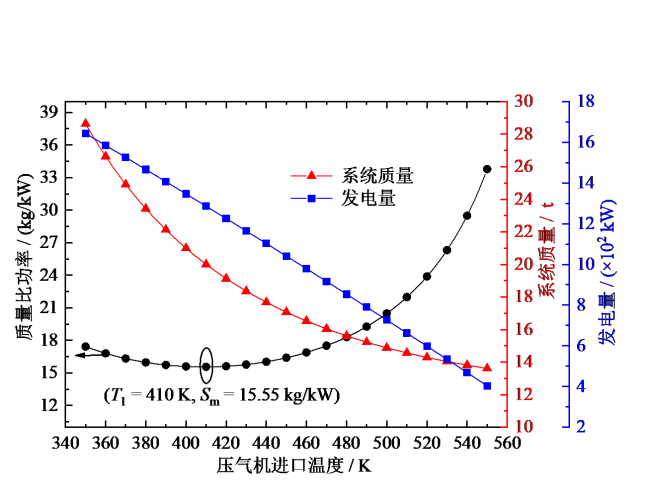
Fig. 5 Overall performance of the system at different inlet temperatures of the compressor图5 不同压气机进口温度下系统总体性能的变化 |
4.2 涡轮进口温度
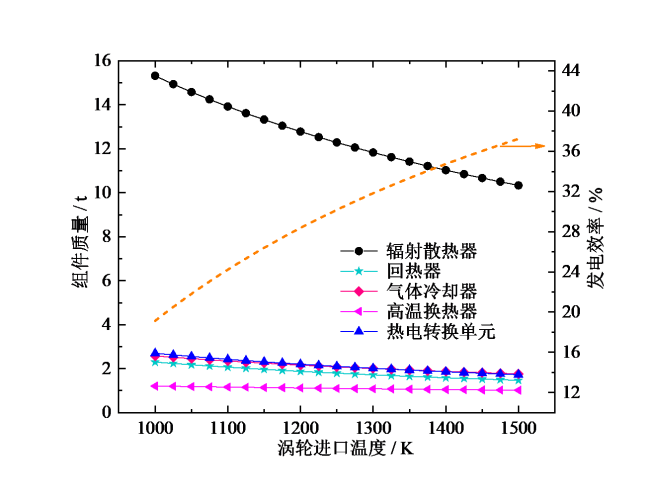
Fig. 6 Variation of the component weight and electrical efficiency at different inlet temperatures of the turbine图6 不同涡轮进口温度下组件质量和发电效率的变化 |
系统总体性能随涡轮进口温度的变化如图7所示。随着涡轮进口温度的升高,系统的总质量由24.11 t下降至16.32 t,降低了32.31%,同时发电效率的升高意味着发电量的增加,温度为1 500 K时,发电量增加至1.9 MW。基于此,随着涡轮进口温度的升高,系统的质量比功率由20.45 kg/kW降低至7.11 kg/kW,降低了65.23%。从以上结果可以看出,提高涡轮进口温度有利于降低系统质量和提高发电性能。与此同时,涡轮进口温度的升高意味着涡轮叶片的热应力也会增加,系统运行的可靠性下降,通常情况下,温度超过1 200 K时,叶片就要选用高性能合金材料。因此提升涡轮叶片的热力性能对提高系统的性能具有重要意义。
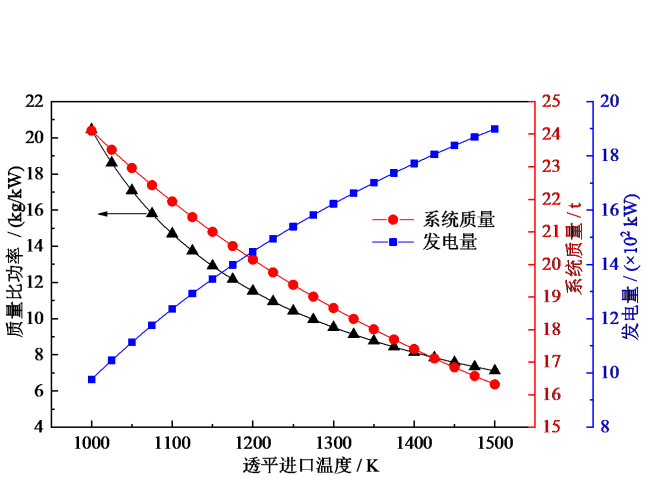
Fig. 7 Overall performance of the system at different inlet temperatures of the turbine图7 不同涡轮进口温度下系统总体性能的变化 |
4.3 压气机压比
压气机压比变化时,会直接影响压气机的运行状态和循环工质的温度和压力等状态参数,进而影响系统的性能。图8显示了压气机压比的变化对系统性能的影响规律。随着压气机压比的增加,发电量呈现先增加后降低的趋势,压比为1.7时,发电量取得最大值1.38 MW,可结合图9进行分析：压气机压比增加时,压气机做功近似线性增加,当压气机压比小于1.7时,涡轮膨胀功快速增加,当压气机压比大于1.7时,涡轮膨胀功上升的速度逐渐放缓,因此压气机压比为1.7时,系统输出功最大,系统的发电效率最高,为27.13%。此外,压气机压比增加时,系统的质量由37.91 t降低至17.00 t,且下降的速度逐渐变慢,主要与系统效率下降时,辐射散热量增加有关。基于上述发电量和系统质量的变化,系统的质量比功率呈现先降低后缓慢增加的变化趋势,当压气机压比为2.3时,质量比功率取得最小值15.19 kg/kW。
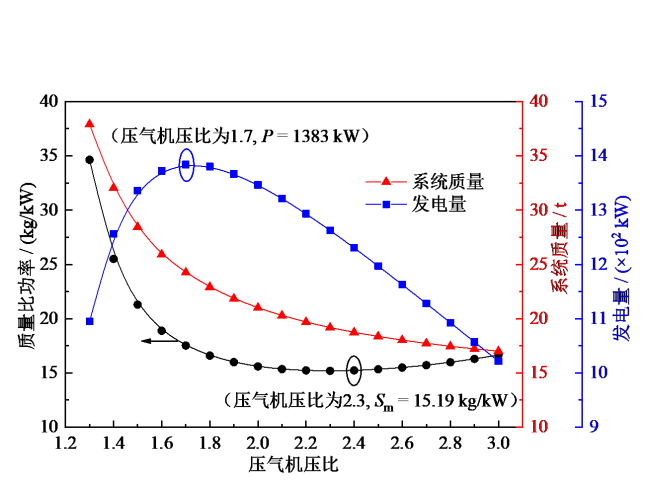
Fig. 8 Overall performance of the system at different pressure ratio of the compressor图8 不同压气机压比下系统总体性能的变化 |
Fig. 9 Electrical efficiency and work of the system at different pressure ratio of the compressor图9 系统发电效率和做功随压气机压比的变化 |
5 热力学参数优化
从上文的讨论可知,压气机进口温度、涡轮进口温度和压气机压比等参数会对系统的性能产生重要的影响,因此有必要进行参数优化从而实现最优的系统性能。同时,考虑到压气机效率、涡轮效率和回热器的回热度等部件的性能参数会对优化结果产生影响,因此,本文采用正交实验法,以质量比功率为优化目标参数,针对不同工况进行热力学参数优化。
基于正交实验法进行工况设计时,将压气机效率、涡轮效率和回热器的回热度三个变量视为三个独立的因素,每个因素分为5个等级。正交表类型为L25(53),因素水平表如表2所示。
Table 2 Factors and levels of the orthogonal experiment表2 正交实验的因素水平表 |
| 因素 | 水平 | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| ηT / % | 0.79 | 0.83 | 0.87 | 0.91 | 0.95 |
| ηC / % | 0.79 | 0.83 | 0.87 | 0.91 | 0.95 |
| α / % | 0.81 | 0.85 | 0.89 | 0.93 | 0.97 |
Table 3 The design conditions of orthogonal experiment and optimization results表3 正交实验设计工况及优化结果 |
| 序号 | 设计工况 | 优化结果 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ηT / % | ηC / % | α / % | 涡轮进口温度 / K | 压气机进口温度 / K | 压气机压比 | 发电效率 / % | 系统质量 / t | 质量比功率 / (kg/kW) | |||
| 1 | 0.81 | 0.79 | 0.79 | 1 500 | 420 | 2.5 | 19.97 | 12.26 | 12.04 | ||
| 2 | 0.81 | 0.83 | 0.83 | 1 500 | 444 | 2.6 | 22.49 | 10.35 | 9.02 | ||
| 3 | 0.81 | 0.87 | 0.87 | 1 500 | 468 | 2.8 | 24.67 | 8.81 | 7.01 | ||
| 4 | 0.81 | 0.91 | 0.91 | 1 500 | 488 | 2.9 | 27.32 | 7.80 | 5.60 | ||
| 5 | 0.81 | 0.95 | 0.95 | 1 500 | 508 | 3.1 | 29.56 | 6.93 | 4.59 | ||
| 6 | 0.85 | 0.79 | 0.83 | 1 500 | 432 | 2.6 | 22.17 | 11.53 | 10.19 | ||
| 7 | 0.85 | 0.83 | 0.87 | 1 500 | 456 | 2.7 | 24.57 | 9.81 | 7.82 | ||
| 8 | 0.85 | 0.87 | 0.91 | 1 500 | 482 | 2.8 | 26.67 | 8.43 | 6.20 | ||
| 9 | 0.85 | 0.91 | 0.95 | 1 500 | 498 | 3.0 | 29.19 | 7.51 | 5.04 | ||
| 10 | 0.85 | 0.95 | 0.79 | 1 500 | 462 | 2.5 | 25.39 | 9.33 | 7.21 | ||
| 11 | 0.89 | 0.79 | 0.87 | 1 500 | 448 | 2.6 | 24.27 | 10.92 | 8.82 | ||
| 12 | 0.89 | 0.83 | 0.91 | 1 500 | 464 | 2.8 | 26.92 | 9.50 | 6.92 | ||
| 13 | 0.89 | 0.87 | 0.95 | 1 500 | 488 | 2.9 | 28.99 | 8.27 | 5.59 | ||
| 14 | 0.89 | 0.91 | 0.79 | 1 500 | 452 | 2.4 | 25.59 | 10.43 | 7.99 | ||
| 15 | 0.89 | 0.95 | 0.83 | 1 500 | 474 | 2.6 | 27.50 | 8.89 | 6.34 | ||
| 16 | 0.93 | 0.79 | 0.91 | 1 500 | 448 | 2.7 | 27.61 | 11.09 | 7.88 | ||
| 17 | 0.93 | 0.83 | 0.95 | 1 500 | 474 | 2.8 | 29.39 | 9.46 | 6.31 | ||
| 18 | 0.93 | 0.87 | 0.79 | 1 500 | 436 | 2.4 | 26.21 | 12.05 | 9.01 | ||
| 19 | 0.93 | 0.91 | 0.83 | 1 500 | 464 | 2.5 | 27.84 | 10.08 | 7.10 | ||
| 20 | 0.93 | 0.95 | 0.87 | 1 500 | 482 | 2.6 | 30.31 | 8.90 | 5.76 | ||
| 21 | 0.97 | 0.79 | 0.95 | 1 500 | 446 | 2.9 | 30.66 | 12.04 | 7.70 | ||
| 22 | 0.97 | 0.83 | 0.79 | 1 500 | 416 | 2.4 | 27.61 | 15.32 | 10.88 | ||
| 23 | 0.97 | 0.87 | 0.83 | 1 500 | 440 | 2.5 | 29.45 | 12.86 | 8.56 | ||
| 24 | 0.97 | 0.91 | 0.87 | 1 500 | 456 | 2.7 | 31.40 | 11.11 | 6.94 | ||
| 25 | 0.97 | 0.95 | 0.91 | 1 500 | 474 | 2.8 | 33.51 | 9.84 | 5.76 | ||
6 结论
为了评估循环关键参数对空间核能布雷顿循环系统性能的影响规律,对该系统进行了热力学参数分析和优化的研究。主要结论如下：
（1）系统的发电效率和质量随着压气机进口温度的升高而降低,但质量比功率随着压气机进口温度升高呈现先降低后升高的变化趋势,即存在最优值使质量比功率取得最小值,当压气机进口温度为410 K时,质量比功率取得最小值,为15.55 kg/kW。
（2）提高涡轮进口温度可以提高系统的发电效率和降低系统的质量,即质量比功率随着涡轮温度的升高而降低。涡轮进口温度与叶片的热力学性能有关,因此提高涡轮叶片的性能对提高系统的效率、促进系统轻量化具有重要意义。
（3）系统的发电效率随着压气机压比的增大呈现先升高后降低的趋势,而且提高压气机压比有利于降低系统的质量。结果表明压气机压比存在最优值使质量比功率取得最小值。
（4）压气机效率、涡轮效率和回热器回热度会对优化结果产生显著影响。采用正交实验法设计不同工况,并进行优化分析,确定了不同工况下参数最优值的范围。结果表明,涡轮进口温度的最优值为温度上限1 500 K,压气机进口温度最优值范围为416 ~ 508 K,压气机压比的最优值范围为2.4 ~ 3.1。