0 引言
近年来,随着膜技术的进一步发展,厌氧膜生物反应器（anaerobic membrane bioreactor, AnMBR）在市政废水[1]、工业废水[2]和畜禽废水[3]等水处理中已有广泛应用。然而,在反应器运行中膜污染问题始终不可避免,在膜污染发生时反应器的处理能力降低,生产成本增加,限制了厌氧膜生物反应器技术的应用[4]。目前,膜污染的机理分析[5,6]及其控制方法[7,8]已被国内外学者深入研究,但关于膜污染监测和模拟的研究报道还相对较少。在膜污染机理分析基础上建立的数学模型是监测膜污染的有效手段。通过分析过程变量与膜污染表征指标之间的数学关系,可以推断出膜运行状态[9,10]。但是,膜污染过程非常复杂,产水流量[11]、污泥浓度[6]和水力停留时间[12]等都会显著影响膜的过滤性能。研究发现,传统的数学模型难以表征复杂因素之间的关系,且大量数据的处理效率不高[13]。基于人工神经网络的适应动态变化、数据并行处理和自学习等特点,相关模型已被用于膜污染的预测研究[14,15]。然而,以上模型预测研究中均忽视了膜污染影响因子间的相互关系,这使得模型的输入数据矩阵结构较为复杂,影响模型输出结果的效率和准确性。
本文基于主成分分析法（principal component analysis, PCA）在多元数据分析中可以利用相关性提取重要数据来降低问题复杂性和难度这一特点[16],提出构建主成分分析-反向传播神经网络（back propagation neural network, BPNN）模型分析膜污染,比较了BPNN与PCA-BPNN两种模型的拟合效果,验证该方法在膜污染预测中的可行性。
1 试验设计与数据来源
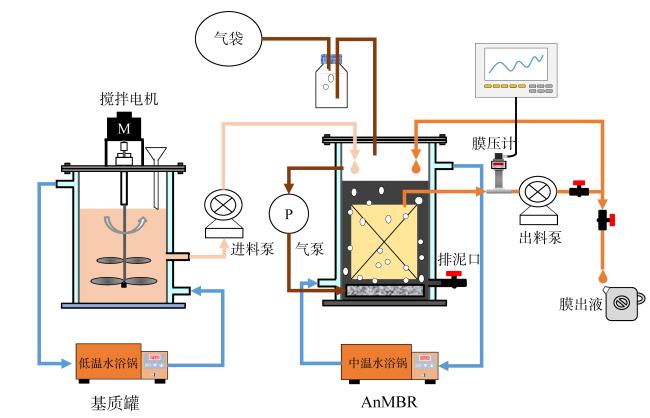
1.1 试验设计
如图1,采用浸没式AnMBR处理取自天津市某垃圾填埋场的垃圾渗滤液,共连续运行102 d;反应器有效容积20 L;水力停留时间（hydraulic retention time, HRT）和固体停留时间（solid retention time, SRT）分别为10 d和100 d,容积负荷为5.6 kgCOD/(m3∙d),反应器内的温度为37℃;膜通量为6 L/(m2∙h),沼气循环流速为9 L/min,产水泵的工作方式为4 min抽滤,1 min休息。
1.2 数据来源
所用数据全部来自之前已开展的AnMBR长期处理垃圾渗滤液的连续试验,发酵原料取自天津市某垃圾填埋场的新鲜渗滤液,运行结果表明平均化学需氧量（chemical oxygen demand, COD）去除率达到92%,膜压62 d内增长缓慢,未出现明显的膜污染[18,19]。各项指标的测试方法如下：COD采用重铬酸钾法测定[20];沼气成分采用气相色谱仪（日本,岛津,GC-8A）测定,色谱柱为Φ 10 mm × 2 m不锈钢色谱柱,载气为氢气,分压为0.38 MPa,流速为20 ~ 30 mL/min;沼气产量采用湿式气体流量计（北京金志业,LML-1）测定;pH的测定采用pH酸度计（瑞士,梅特勒-托利多,FE20）;总固体（total solid, TS）和挥发性固体（volatile solid, VS）含量采用重量法测定[21];膜压采用压力传感器（西安闵波,ESM-PS）测定;电导率采用电导率仪（瑞士,梅特勒-托利多,FE38）测定。
2 理论分析
2.1 主成分分析
假设有样本$M=\left\{ {{Y}^{1}},{{Y}^{2}},{{Y}^{3}},......,{{Y}^{r}} \right\}$,每个样本有n维特征值${{Y}_{i}}=\left\{ y_{1}^{i},y_{2}^{i},y_{3}^{i},......,y_{n}^{i} \right\}$。对所有特征进行中心化：
$\overline{{{y}_{n}}}=\frac{1}{M}\sum\limits_{i=1}^{M}{y_{n}^{i}}$ (1)
建立协方差矩阵：
$\mathbf{A}=\left[ \begin{matrix} \operatorname{cov}\left( {{x}_{1}},{{x}_{1}} \right) \\ \operatorname{cov}\left( {{x}_{2}},{{x}_{1}} \right) \\ ... \\ \operatorname{cov}\left( {{x}_{n}},{{x}_{1}} \right) \\ \end{matrix}\begin{matrix} ... \\ ... \\ {} \\ ... \\ \end{matrix}\begin{matrix} \operatorname{cov}\left( {{x}_{1}},{{x}_{2}} \right) \\ \operatorname{cov}\left( {{x}_{2}},{{x}_{2}} \right) \\ ... \\ \operatorname{cov}\left( {{x}_{n}},{{x}_{2}} \right) \\ \end{matrix}\begin{matrix} ... \\ ... \\ {} \\ ... \\ \end{matrix}\begin{matrix} \operatorname{cov}\left( {{x}_{1}},{{x}_{n}} \right) \\ \operatorname{cov}\left( {{x}_{2}},{{x}_{n}} \right) \\ ... \\ \operatorname{cov}\left( {{x}_{n}},{{x}_{n}} \right) \\ \end{matrix} \right]$ (2)
矩阵A对角线是特征x1、x2…xn的方差,而非对角线上则为协方差,协方差求解公式为：
$\operatorname{cov}\left( {{x}_{n}},{{x}_{n}} \right)=\frac{\sum\limits_{i=1}^{M}{\left( x_{n}^{i}-\overline{{{x}_{n}}} \right)\left( x_{n}^{i}-\overline{{{x}_{n}}} \right)}}{M-1}$ (3)
通过公式（3）可以得到这m个样本在n维特征下的协方差矩阵A。利用矩阵相关知识求解特征值λ与特征向量μ,将特征值从大到小进行排列,可知其主成分计算公式（4）。
${{Z}_{k}}={{\left( {{u}_{k}} \right)}^{T}}\mathbf{A}$ (4)
利用公式（5）可以求解第k个主成分的贡献率,并进行累加得到累计贡献率。
${{W}_{k}}=\frac{{{\lambda }_{k}}}{\sum\limits_{k=1}^{n}{{{\lambda }_{k}}}}$ (5)
2.2 BP神经网络
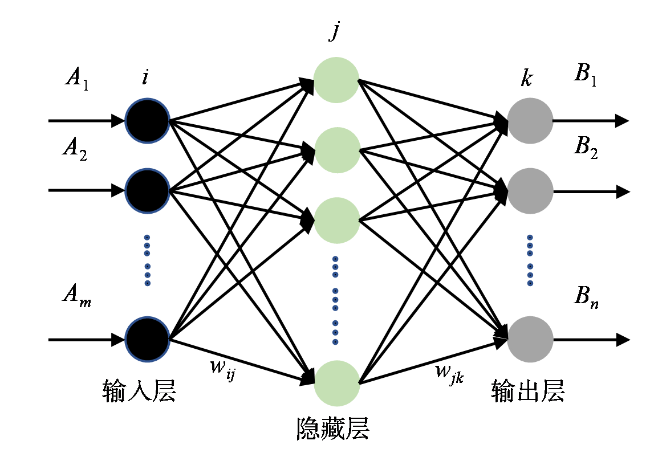
Fig. 2 Topological structure of BP neural network图2 BP神经网络的拓扑结构 |
假定BP神经网络输入层节点为m个;隐藏层节点l个;输出层节点为n个;wij为输入层与隐藏层神经元之间的权值;wjk为隐藏层第j个神经元与输出层第k个神经元之间的权值;激活函数为sigmoid型函数[23],如公式（6）所示;隐藏层的输出如公式（7）所示。
$f\left( x \right)=\frac{1}{1+{{\text{e}}^{-x}}}$ (6)
${{H}_{j}}=f\left( \sum\limits_{i=1}^{n}{{{w}_{ij}}{{x}_{i}}-{{a}_{j}}} \right)\text{ (}j=1,2,...,l)$ (7)
式中：Hj是隐藏层第j个神经元的输出; f是激活函数;aj是隐藏层第j个神经元的阈值;xi是输入层第i个神经元的输入;wij是输入层第i个神经元与隐藏层第j个神经元之间的权值;l是隐藏层的节点数。
输出层的输出计算公式如式（8）所示：
${{O}_{k}}=\sum\limits_{j=1}^{l}{{{H}_{j}}{{w}_{jk}}-{{b}_{k}}}\text{ (}k=1,2,...,n)$ (8)
式中：Ok是输出层第k个神经元的预测输出;bk是输出层第k个神经元的阈值;Hj是隐藏层第j个神经元的输出。
3 模型构建
根据之前的理论分析,基于PCA-BPNN的膜污染预测模型建立过程如图3所示。
Fig. 3 Construction of membrane fouling prediction model图3 膜污染预测模型的构建 |
（1）选取影响因素。在连续试验所有数据中选取与膜污染相关的11个因素,采用统计产品与服务解决方案（statistical product and service solutions, SPSS）进行相关性分析,选取与膜污染表征指标渗透率相关系数较大的因子作为输入。
（2）数据归一化处理。对选取的输入指标数据进行归一化处理,公式如式（9）所示。
${{X}_{n}}=\frac{X-{{X}_{\min }}}{{{X}_{\max }}-{{X}_{\min }}}$ (9)
式中：Xn是归一化数据;X是实际数据;Xmin是数据集中的最小值;Xmax是数据集中的最大值。
（3）PCA提取主成分。数据归一化处理后进行主成分分析,提取累计贡献率超过85%的主成分作为神经网络模型的输入。
（4）构建拓扑结构。确定输入、输出节点数,通过经验公式（10）确定隐藏层的节点数。
$h=\sqrt{m+n}+a$ (10)
式中：h是隐藏层节点数目;a是1 ~ 10之间的调节常数。
（5）模型训练测试。数据集划分为训练集和测试集,模型的评价指标为相对误差,计算为：
${{E}_{\text{r}}}=\left| \frac{Y_{t}^{\left( i \right)}-{{Y}^{\left( i \right)}}}{Y_{t}^{\left( i \right)}} \right|\times 100\text{ }\!\!%\!\!\text{ }$ (11)
式中：Er是相对误差,%;Yt(i)是第i个实际输出;Y(i)是第i个预测输出。
4 结果与讨论
4.1 影响因素的相关性分析
在膜生物反应器处理废水过程中,膜污染成型
及其机理复杂,影响因素较多。据报道,已有的膜污染预测模型中常见的输入特征有进料COD浓度、污泥浓度、有机负荷、出水pH等[14,15],主要通过文献分析确定,无具体的科学依据。如表1所示,本研究选择10个影响因素（1 ~ 10号）作为膜污染预测模型的输入,以渗透率为输出表征膜污染状态。为了简化模型结构,提高模型拟合效果,对数据集中的数据进行相关性分析,得到的相关系数矩阵如表2所示。可以看出,与渗透率相关系数在0.5以上的因素有5个,分别为运行时间、进料COD浓度、电导率、总固体和膜压周期波动速率。同时,进一步分析可知,这些输入因素之间具有一定的相关性,使得BP神经网络模型的准确性受到影响,有必要对输入数据进行主成分分析。
Table 1 Influencing factors of membrane pollution表1 膜污染影响因素 |
| 序号 | 影响因素 | 符号表示 |
|---|---|---|
| 1 | 运行时间 | X1 |
| 2 | pH | X2 |
| 3 | CH4/CO2 | X3 |
| 4 | 进料COD | X4 |
| 5 | 出料COD | X5 |
| 6 | 电导率 | X6 |
| 7 | 总固体 | X7 |
| 8 | 挥发性固体 | X8 |
| 9 | 产水流量 | X9 |
| 10 | 膜压周期波动速率 | X10 |
| 11 | 渗透率 | X11 |
Table 2 Correlation coefficient matrix among influencing factors of membrane fouling表2 膜污染影响因素之间的相关系数矩阵 |
| 因素 | 相关系数 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | |
| X1 | 1.000 | 0.005 | -0.551 | 0.568 | -0.700 | 0.785 | 0.968 | 0.152 | -0.542 | 0.708 | -0.901 |
| X2 | 0.005 | 1.000 | -0.138 | -0.122 | -0.347 | 0.148 | -0.021 | 0.033 | 0.025 | -0.069 | 0.062 |
| X3 | -0.551 | -0.138 | 1.000 | -0.109 | 0.652 | -0.777 | -0.583 | -0.355 | 0.150 | -0.319 | 0.392 |
| X4 | 0.568 | -0.122 | -0.109 | 1.000 | -0.157 | 0.149 | 0.447 | 0.155 | -0.741 | 0.406 | -0.648 |
| X5 | -0.700 | -0.347 | 0.652 | -0.157 | 1.000 | -0.848 | -0.663 | -0.199 | 0.220 | -0.408 | 0.496 |
| X6 | 0.785 | 0.148 | -0.777 | 0.149 | -0.848 | 1.000 | 0.831 | 0.350 | -0.199 | 0.470 | -0.551 |
| X7 | 0.968 | -0.021 | -0.583 | 0.447 | -0.663 | 0.831 | 1.000 | 0.255 | -0.386 | 0.730 | -0.870 |
| X8 | 0.152 | 0.033 | -0.355 | 0.155 | -0.199 | 0.350 | 0.255 | 1.000 | -0.007 | 0.210 | -0.219 |
| X9 | -0.542 | 0.025 | 0.150 | -0.741 | 0.220 | -0.199 | -0.386 | -0.007 | 1.000 | -0.100 | 0.478 |
| X10 | 0.708 | -0.069 | -0.319 | 0.406 | -0.408 | 0.470 | 0.730 | 0.210 | -0.100 | 1.000 | -0.876 |
| X11 | -0.901 | 0.062 | 0.392 | -0.648 | 0.496 | -0.551 | -0.870 | -0.219 | 0.478 | -0.876 | 1.000 |
4.2 主成分分析
Table 3 Total variance interpretation表3 总方差解释 |
| 主成分 | 初始特征值 | 提取载荷平方和 | ||||
|---|---|---|---|---|---|---|
| 总计 | 方差贡献率 / % | 累积贡献率 / % | 总计 | 方差贡献率 / % | 累积贡献率 / % | |
| 1 | 3.521 | 70.428 | 70.428 | 3.521 | 70.428 | 70.428 |
| 2 | 0.885 | 17.706 | 88.134 | 0.885 | 17.706 | 88.134 |
| 3 | 0.470 | 9.400 | 97.534 | / | / | / |
| 4 | 0.103 | 2.053 | 99.587 | / | / | / |
| 5 | 0.021 | 0.413 | 100.000 | / | / | / |
Table 4 Correlation coefficient matrix between principal components and corresponding variables表4 主成分与对应变量的相关系数矩阵 |
| 变量 | 相关系数 | |
|---|---|---|
| 主成分1 | 主成分2 | |
| X1 | 0.978 | 0.002 |
| X4 | 0.569 | 0.781 |
| X6 | 0.808 | -0.497 |
| X7 | 0.974 | -0.133 |
| X10 | 0.799 | 0.105 |
Table 5 Principal component factor load matrix表5 主成分因子载荷矩阵 |
| 因子 | 因子载荷 | |
|---|---|---|
| 主成分1 | 主成分2 | |
| X1 | 0.521 | 0.002 |
| X4 | 0.303 | 0.830 |
| X6 | 0.431 | -0.528 |
| X7 | 0.519 | -0.141 |
| X10 | 0.426 | 0.112 |
通过表5中的数据,可知主成分的表达式为：
$\left[ \begin{matrix} {{y}_{1}} \\ {{y}_{2}} \\ \end{matrix} \right]=\left[ \begin{matrix} 0.521 & 0.002 \\ 0.303 & 0.830 \\ 0.431 & -0.528 \\ 0.519 & -0.141 \\ 0.426 & 0.112 \\ \end{matrix} \right]T\times \left[ \begin{matrix} {{x}_{1}} \\ {{x}_{4}} \\ {{x}_{6}} \\ {{x}_{7}} \\ {{x}_{10}} \\ \end{matrix} \right]$ (12)
4.3 基于PCA优化的模型预测
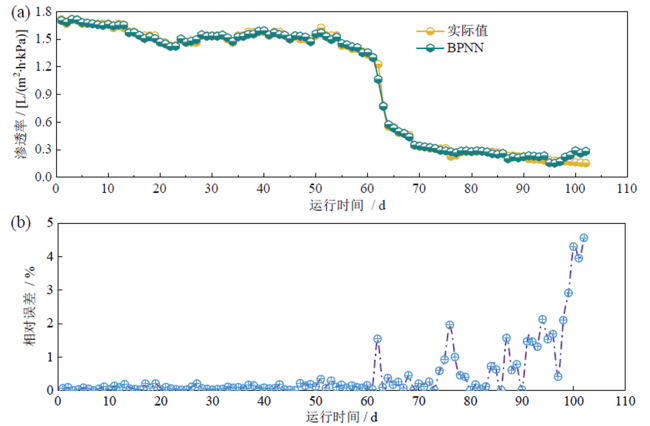
Fig. 4 Fitting effect of single neural network model: (a) permeability variation; (b) the relative error图4 单一神经网络模型的拟合效果：（a）渗透率变化;（b）相对误差 |
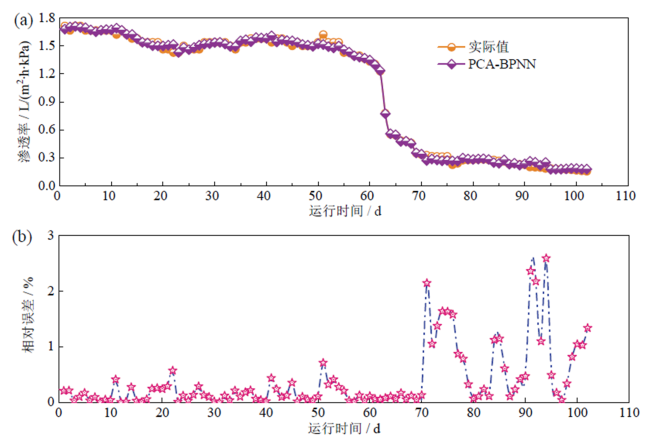
Fig. 5 Fitting effect of PCA optimized neural network model: (a) permeability variation; (b) the relative error图5 基于PCA优化神经网络模型的拟合效果：（a）渗透率变化;（b）相对误差 |
4.4 膜污染影响因素分析
在人工神经网络模型预测膜污染的研究中,输入变量（即膜污染影响因素）的选择十分重要,所选因素必须是独立的,不存在明显的数学关系,并且与输出变量之间有密切的联系。研究表明,以进料浓度、操作时间、跨膜压力等作为输入变量,人工神经网络模型预测膜污染可以取得较好的结果[31]。本研究通过单一BP神经网络模型确定了运行时间、进料COD、电导率等输入变量与输出变量渗透率之间的贡献关系,结果如图6所示。可以看出,在5个输入变量中,特征变量污泥浓度和运行时间在膜污染预测中的贡献较大,分别为34.9%和22.6%,以电导率的贡献最小,仅为3.9%。由于神经网络模型的拟合效果取决于输入和输出变量之间的关系,结合相关性分析结果可知,运行时间、污泥浓度是影响模型拟合的关键因素。同时,由PCA分析可知,在主成分1中也是运行时间和污泥浓度两个变量的因子解释度相对较大。因此可知,在不考虑运行时间的情况下,污泥浓度是影响膜污染的最主要特征。在后续的工程研究中,合理地控制反应器污泥浓度是延缓膜污染发生的有效方法。
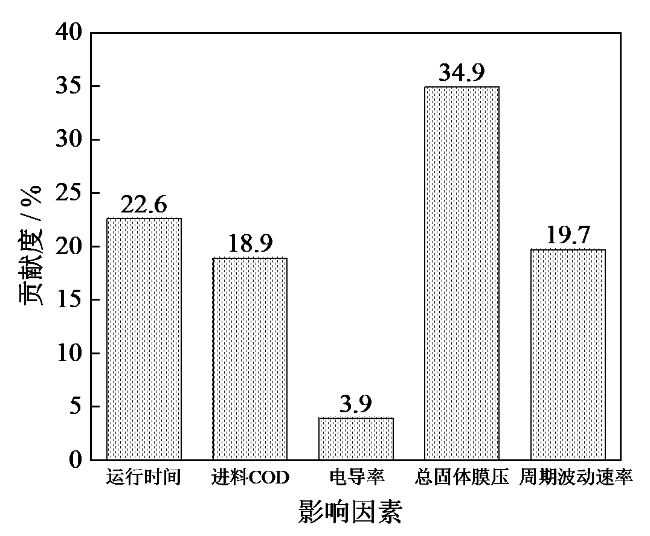
Fig. 6 Contribution analysis of membrane pollution factors图6 膜污染因素贡献度分析 |
5 结论
针对膜污染预测模型中输入变量的有效选取和拓扑结构复杂问题,本文引入主成分分析方法优化神经网络模型,对膜污染进行了深入分析。利用相关性分析确定了与膜污染表征指标渗透率相关的5个输入参数,分别为运行时间、进料COD、电导率、总固体和膜压周期波动速率。同时,针对输入变量间存在信息重叠这一问题,采用PCA进行数据的降维处理,以累计贡献率为88.1%的两个主成分作为模型的输入,避免了因输入变量间的相关性造成的计算复杂化。结合模型的贡献度分析和主成分分析的因子载荷矩阵,可以发现污泥浓度是影响膜污染的最主要因素,贡献度为34.9%。比较PCA-BPNN模型与单一BPNN模型的预测效果,发现经PCA处理后的模型预测准确率更高,平均相对误差由4.6%降到3.8%。因此,将主成分分析和人工神经网络相结合应用于膜污染分析具有可行性,可以为膜污染分析研究提供一种新的思路。