0 引言
1 风力机叶片非线性单元模型
1.1 叶片构型及变形
风力机叶片是由一定几何形状的翼型与多种材料铺层所形成的,由于截面形状较为特殊,且复合材料铺层的各向异性同一截面的铺层厚度不一,因此具有重心、剪心、扭心不共点的特性和材料的各向异性特性。图1为10 MW风力机叶片的主要截面形状。
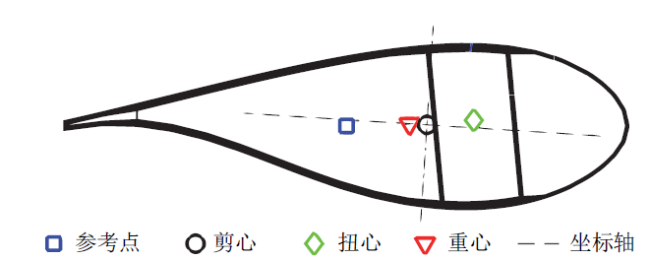
Fig. 1 The section of wind turbine blade图1 风力机叶片截面 |
在叶片根部建立全局坐标系（XG,YG,ZG）,XG与风轮平面垂直,ZG与叶根平面垂直。以各截面的剪心作为原点建立各截面的局部弹性坐标系（XE,YE,ZE）,三个坐标轴的指向与全局坐标系一致,定义此时的叶片状态为直叶片的参考构型。
将各截面的剪心连成一线,该连线则为叶片的轴线。基于几何精确梁的平截面假设,叶片的变形和叶片的预弯预扭初始构型,可视作是由各截面XE-YE平面上的平移与绕ZE轴的转动所形成的。
1.2 截面转动描述
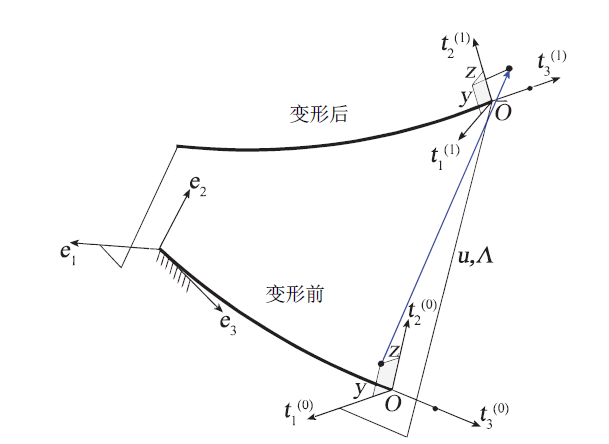
Fig. 2 The variation of section rotation before and after beam deformation图2 截面转动在梁变形前后的变化关系 |
图2中,（e1, e2, e3）为全局坐标系的基向量,当梁发生变形后,同一截面的局部坐标系基向量t(0)变成了t(1),其中的转动变化可通过三阶方向余弦矩阵Λ来表示
$\mathbf{t}_{_{i}}^{\text{(1)}}=\mathbf{\Lambda t}_{i}^{\text{(0)}} \left( i=1,2,3 \right)$ (1)
方向余弦矩阵Λ有9个分量,计算效率低,截面转动的更新也比较复杂,欧拉四元数是空间三维转动非奇异的最少参数表达,因此本文采用欧拉四元数描述截面的转动[15]。四元数与方向余弦矩阵的关系为
$\mathsf{\hat{q}}=\left( {{q}_{0}}\text{,}\mathbf{q} \right)=\left( {{q}_{0}}\text{,}{{q}_{1}}\text{,}{{q}_{2}}\text{,}{{q}_{3}} \right)$ (2)
$\mathsf{\Lambda }=\left( 2q_{0}^{2}-1 \right)\mathsf{I}+2{{q}_{0}}\mathsf{\tilde{q}}+2\mathsf{q}{{\mathsf{q}}^{\text{T}}}$ (3)
式中：q0、q1、q2、q3为四元数,$q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}\text{=}1$,定义$\left( \tilde{ } \right)$为其对应的斜对称矩阵。
由欧拉四元数性质可知,q0可通过q计算所得,则可以用节点线位移u、节点欧拉参数q,定义节点的位移向量为
${{\mathsf{d}}_{\mathsf{i}}}=\left[ \begin{matrix} \begin{matrix} \begin{matrix} {{u}_{i1}} & {{u}_{i2}} \\ \end{matrix} & {{u}_{i3}} & {{q}_{i1}} \\ \end{matrix} & {{q}_{i2}} & {{q}_{i3}} \\ \end{matrix} \right]$ (4)
通过四元数法与增量转动法得到增量四元数可实现旋转的可加性,用于确定截面转动。四元数增量可以使用指数映射的方式
$\mathsf{\hat{q}}+\text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{q}}=\exp \left( \text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}/2 \right)\circ \mathsf{\hat{q}}$ (5)
$\exp \left( \text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}/2 \right)=\hat{1}+\frac{1}{2!}\frac{\text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}}{2}\circ \frac{\text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}}{2}+\frac{1}{3!}\frac{\text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}}{2}\circ \frac{\text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}}{2}+\cdots $ (6)
式中：$\text{ }\!\!\Delta\!\!\text{ }\mathsf{\hat{\theta }}$为截面微小转动增量的纯四元数;$\circ $为四元数乘法。
节点的角速度和角加速度与四元数的关系为
${{\mathbf{T}}_{q}}=2\left( {{q}_{0}}\mathbf{I}+\frac{\mathbf{q}{{\mathbf{q}}^{\text{T}}}}{{{q}_{0}}}+\tilde{q} \right)$ (7)
$\mathsf{\dot{\theta }}={{\mathsf{T}}_{q}}\mathsf{\dot{q}}$ (8)
$\mathsf{\ddot{\theta }}={{\mathsf{T}}_{q}}\mathsf{\ddot{q}}$ (9)
式中：定义$\left( \dot{ } \right)$和$\left( \ddot{ } \right)$分别为其对时间的一次和二次导数。
对于10 MW叶片截面节点的选择,本文采用Legendre-Gauss-Lobatto积分法则中的积分点。
1.3 动力学平衡方程
几何精确梁理论采用一阶假设的Reissner应变,定义Reissner应变Γ为平动应变向量,应变K为转动应变向量,则截面等效力N、M与应变Γ、K的关系,即本构关系为
$\left( \begin{matrix} \mathbf{N} \\ \mathbf{M} \\ \end{matrix} \right)=\mathsf{S}\left( \begin{matrix} \mathbf{\Gamma } \\ \mathbf{K} \\ \end{matrix} \right)=\left( \begin{matrix} {{\mathsf{S}}_{\text{A}}} & {{\mathsf{S}}_{\text{B}}} \\ \mathsf{S}_{\text{B}}^{\text{T}} & {{\mathsf{S}}_{\text{D}}} \\ \end{matrix} \right)\left( \begin{matrix} \mathbf{\Gamma } \\ \mathbf{K} \\ \end{matrix} \right)$ (10)
$\mathbf{\Gamma }=\mathbf{\Lambda {u}'}-{{\mathbf{\Gamma }}_{\text{0}}}$ (11)
$\mathsf{\hat{K}}=\left( 0,{{K}_{1}},{{K}_{2}},{{K}_{3}} \right)=2\mathsf{\hat{q}}\circ \mathsf{{\hat{q}}'}-{{\mathsf{\hat{K}}}_{0}}$ (12)
式中：S为6 × 6的截面刚度矩阵;N为截面剪切力与轴向力;M为截面弯矩与扭矩;Γ0、K0为风力机叶片初始构型的预弯预扭参数;定义${{\left( {} \right)}^{\prime }}$为在参考构形中对截面在Z轴上坐标的导数。
根据DTU所提供的10 MW风力机叶片数据,建立叶片三维模型,再根据Lobatto积分点选择相应叶片截面,提取对应叶片截面的有限元单元几何数据,加上叶片铺层材料的数据,导入专业分析截面软件VABS计算得到叶片截面刚度矩阵[16]。
结合虚功原理,得到叶片单元的内力、外力和惯性力的虚功平衡方程为
$\text{ }\!\!\delta\!\!\text{ }\mathsf{W}_{\text{int}}^{\text{e}}-\text{ }\!\!\delta\!\!\text{ }\mathsf{W}_{\text{ext}}^{\text{e}}+\text{ }\!\!\delta\!\!\text{ }\mathsf{W}_{\text{inert}}^{\text{e}}=0$ (13)
根据Gauss-Lobatto积分法则,用微元求积法得到离散的叶片单元的内力、外力和惯性力的虚功为$\text{ }\!\!\delta\!\!\text{ }\mathsf{W}_{\text{int}}^{\text{e}}=\text{ }\!\!\delta\!\!\text{ }{{\mathsf{d}}^{\text{e}}}^{\text{T}}{{\mathsf{R}}_{\text{int}}}$、$\text{ }\!\!\delta\!\!\text{ }\mathsf{W}_{\text{ext}}^{\text{e}}=\text{ }\!\!\delta\!\!\text{ }{{\mathsf{d}}^{\text{e}}}^{\text{T}}{{\mathsf{R}}_{\text{ext}}}$、$\text{ }\!\!\delta\!\!\text{ }\mathsf{W}_{\text{inert}}^{\text{e}}=\text{ }\!\!\delta\!\!\text{ }{{\mathsf{d}}^{\text{e}}}^{\text{T}}{{\mathsf{R}}_{\text{inert}}}$,则全局坐标系下的叶片单元平衡方程[9]为
${{\mathsf{R}}_{\text{int}}}-{{\mathsf{R}}_{\text{ext}}}+{{\mathsf{R}}_{\text{inert}}}=0$ (14)
1.4 平衡方程的线性化
为了求解转动叶片的频率,可通过在平衡点对叶片非线性平衡方程做局部线性化展开,则得到叶片单元的内力、外力和惯性力的线性增量为$\text{ }\!\!\Delta\!\!\text{ }{{\mathsf{R}}_{\text{int}}}={{\mathsf{K}}_{\text{int}}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}$、$\text{ }\!\!\Delta\!\!\text{ }{{\mathsf{R}}_{\text{ext}}}={{\mathsf{K}}_{\text{ext}}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}$、$\text{ }\!\!\Delta\!\!\text{ }{{\mathsf{R}}_{\text{inert}}}={{\mathsf{K}}_{\text{inert}}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}+$ ${{\mathsf{C}}_{\text{inert}}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{\dot{d}}+{{\mathsf{M}}_{\text{inert}}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{\ddot{d}}$,因此增量形式的线性化平衡方程[9]为
$\mathsf{M}\text{ }\!\!\Delta\!\!\text{ }\mathsf{\ddot{d}}+\mathsf{C}\text{ }\!\!\Delta\!\!\text{ }\mathsf{\dot{d}}+\mathsf{K}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}=0$ (15)
式中：平衡方程参数为$\mathsf{K}={{\mathsf{K}}_{\text{int}}}-{{\mathsf{K}}_{\text{ext}}}+{{\mathsf{K}}_{\text{inert}}}$;$\mathsf{M}={{\mathsf{M}}_{\text{inert}}}$;$\mathsf{C}={{\mathsf{C}}_{\text{inert}}}$。
对式（14）使用牛顿迭代法进行求解,迭代到第i步时得到非平衡位移向量d(i)以及平衡方程残差${{\mathsf{R}}^{\text{(}i\text{)}}}=\mathsf{R}_{\text{int}}^{\text{(}i\text{)}}-\mathsf{R}_{\text{ext}}^{\text{(}i\text{)}}+\mathsf{R}_{\text{inert}}^{\text{(}i\text{)}}$,再根据式（15）可得到位移增量$\text{ }\!\!\Delta\!\!\text{ }{{\mathsf{d}}^{\text{(}i\text{)}}}$,从而得到下一步的位移向量。
当叶片从静止加速到所设定的转速且方程达到平衡状态时,在平衡位置处线性化质量矩阵及刚度矩阵,由特征值分解计算转动叶片的模态的公式如下
$\left( \mathsf{K}-\omega _{n}^{2}\mathsf{M} \right)\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}=0$ (16)
1.5 稳态位置求解
叶片非线性系统动力学平衡方程的求解需要使用具有预测-校正特性的方法,此处采用广义-α时间预测法[12]。
广义-α时间预测-校正的方法对增量平衡方程的求解为
${{\mathsf{\bar{K}}}^{t}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}={{\mathsf{\bar{h}}}^{t}}$ (17)
${{\mathsf{\bar{K}}}^{t}}=\left( 1-{{\alpha }_{f}} \right){{\mathsf{K}}^{t}}+\frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }{{t}^{2}}}\left( 1-{{\alpha }_{m}} \right){{\mathsf{M}}^{t}}\text{+}\frac{\zeta }{\eta \text{ }\!\!\Delta\!\!\text{ }t}\left( 1-{{\alpha }_{f}} \right){{\mathsf{C}}^{t}}$(18)
$\begin{align} & {{{\mathsf{\bar{h}}}}^{t}}={{\mathsf{R}}^{t}}+\left( 1-{{\alpha }_{m}} \right){{\mathsf{M}}^{t}}\left( \frac{1}{2\eta }{{{\mathsf{\ddot{d}}}}_{t}}+\frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }t}{{{\mathsf{\dot{d}}}}_{t}} \right)\text{+} \\ & \left( 1-{{\alpha }_{f}} \right){{\mathsf{C}}^{t}}\left( \frac{\zeta -2\eta }{2\eta }\text{ }\!\!\Delta\!\!\text{ }t{{{\mathsf{\ddot{d}}}}_{t}}+\frac{\zeta }{\eta }{{{\mathsf{\dot{d}}}}_{t}} \right) \end{align}$ (19)
式中：${{\mathsf{K}}^{t}}$、${{\mathsf{M}}^{t}}$、${{\mathsf{C}}^{t}}$、${{\mathsf{R}}^{t}}$分别为t时刻的刚度矩阵、质量矩阵、阻尼矩阵、平衡方程残差;${{\alpha }_{m}}=\frac{2\rho -1}{\rho +1}$;${{\alpha }_{f}}=\frac{\rho }{\rho +1}$;$\zeta =\frac{1}{2}-{{\alpha }_{m}}+{{\alpha }_{f}}$;$\eta =\frac{1}{4}{{\left( 1-{{\alpha }_{m}}+{{\alpha }_{f}} \right)}^{2}}$;ρ是高频耗散的谱半径[12],ρ = 1时为无数值耗散,ρ = 0时为数值耗散最大,根据求解问题ρ可取[0,1],本文选用ρ = 0.05。
由位移增量得到速度和加速度增量为：
$\text{ }\!\!\Delta\!\!\text{ }\mathsf{\ddot{d}}=-\frac{1}{2\eta }{{\mathsf{\ddot{d}}}^{t}}-\frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }t}{{\mathsf{\dot{d}}}^{t}}+\frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }{{t}^{2}}}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}$ (20)
$\text{ }\!\!\Delta\!\!\text{ }\mathsf{\dot{d}}=\frac{2\eta -\zeta }{2\eta }\text{ }\!\!\Delta\!\!\text{ }t{{\mathsf{\ddot{d}}}^{t}}-\frac{\zeta }{\eta }{{\mathsf{\dot{d}}}^{t}}+\frac{\zeta }{\eta \text{ }\!\!\Delta\!\!\text{ }t}\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}$ (21)
由$\text{ }\!\!\Delta\!\!\text{ }\mathsf{d}$、$\Delta \dot{d}$、$\Delta \ddot{d}$得到$t+\Delta t$时刻的近似解,然后迭代求解出$t+\Delta t$时刻的精确解$\mathsf{d}$、$\dot{d}$、$\ddot{d}$,从而确定叶片非线性动力学系统的平衡状态。
2 算例验证
本节根据以上几何精确梁理论公式,编写对应的MATLAB程序,构建几何精确梁模型,并用以下三个算例验证几何精确梁理论对静力学及动力学特性描述的准确性。
2.1 纯弯曲梁
为了体现几何精确梁理论描述非线性大变形的准确性,以纯弯曲悬臂梁的静力学变形作为算例。根据纯弯理论可得,梁仅在自由端受到一定弯矩后,梁轴线会变形成一段圆弧,其对应曲率为κ = M/(EI),M为弯矩,EI为梁截面刚度。现对梁长L = 1 m的悬臂梁自由端施加的弯矩M = EIθ/L,则得到变形后梁轴线的曲率解析值为θ。
图3为几何精确梁理论分析不同的θ所对应的弯矩对悬臂梁变形的结果,与相应的解析值作为对比,两者结果基本符合。
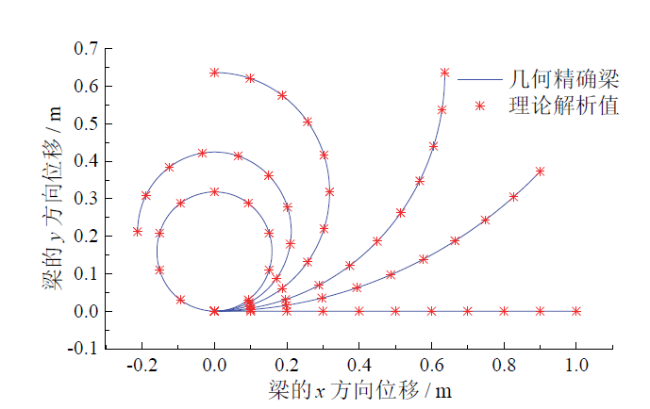
Fig. 3 Pure bending beam deformation图3 纯弯曲梁变形 |
2.2 叶片静挠度
为了体现几何精确梁理论能对结构不规则且具有复合材料铺层的10 MW风力机叶片进行准确的变形描述,对叶片末端分别在挥舞（垂直于风轮平面的方向）、摆振方向（风轮平面所在的方向）施加 -100 000 N的力,利用几何精确梁理论计算其静挠度,并与使用软件Abaqus的计算结果做对比,分别如图4所示,两者结果基本符合。
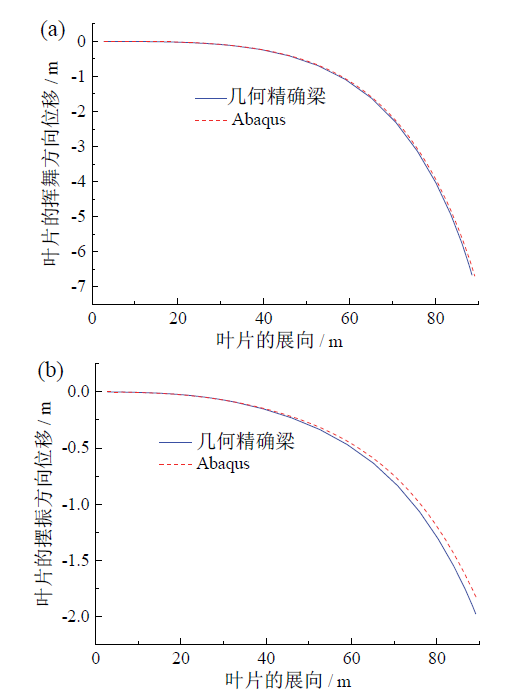
Fig. 4 Static deflection in flapwise direction (a) and edgewise direction (b)图4 挥舞方向（a）和摆振方向（b）的静挠度 |
2.3 旋转梁的动力特性
为了体现几何精确梁理论对旋转物体动力学特性的准确性,以定轴旋转梁为研究对象,此矩形截面梁的几何尺寸比例与叶片的尺寸比例相近,长度L = 7 m,横截面宽b = 0.5 m、高h = 0.15 m,材料为叶片结构常用的环氧树脂,弹性模量E = 4.0 GPa,剪切模量G = 1.481 4 GPa,密度ρ = 1 140 kg/m3,泊松比μ = 0.35。
表1为使用几何精确梁模型,结合21个Lobatto积分点,计算该定轴旋转梁分别在0 r/min、10 r/min、20 r/min转速下的前五阶固有频率结果,以及使用软件ANSYS Workbench对该梁做有限元分析的结果,该有限元模型采用的是Beam188梁单元,该梁单元考虑了剪切效应,每个节点有3个平动自由度,3个转动自由度,共6个自由度。算例单元数为234个。
Table 1 Natural frequency comparison of rotating beam表1 旋转梁的固有频率对比 |
| 转速 / (r/min) | 阶次 | 几何精确梁 / Hz | ANSYS / Hz | 相对误差 / % |
|---|---|---|---|---|
| 0 | 1 | 0.926 | 0.926 | 0.004 |
| 2 | 3.077 | 3.075 | 0.052 | |
| 3 | 5.792 | 5.790 | 0.031 | |
| 4 | 16.167 | 16.154 | 0.082 | |
| 5 | 18.876 | 18.814 | 0.330 | |
| 10 | 1 | 0.942 | 0.942 | 0.008 |
| 2 | 3.081 | 3.076 | 0.182 | |
| 3 | 5.806 | 5.804 | 0.031 | |
| 4 | 16.181 | 16.168 | 0.082 | |
| 5 | 18.880 | 18.817 | 0.336 | |
| 20 | 1 | 0.989 | 0.989 | 0.001 |
| 2 | 3.096 | 3.078 | 0.579 | |
| 3 | 5.848 | 5.846 | 0.028 | |
| 4 | 16.223 | 16.210 | 0.078 | |
| 5 | 18.893 | 18.828 | 0.344 |
表1的对比结果表明了几何精确梁模型可以用较少的自由度得出旋转梁的高精度动力学特性。
3 叶片的模态分析
Table 2 Modal analysis results of static blade表2 静止叶片的模态分析结果 |
| 阶次 | 振型 | 固有频率 / Hz | 相对误差 / % | |
|---|---|---|---|---|
| 本文 | 文献[13] | |||
| 1 | 一阶挥舞 | 0.603 | 0.61 | 1.08 |
| 2 | 一阶摆振 | 0.936 | 0.93 | 0.67 |
| 3 | 二阶挥舞 | 1.737 | 1.74 | 0.16 |
| 4 | 二阶摆振 | 2.813 | 2.76 | 1.91 |
| 5 | 三阶挥舞 | 3.583 | 3.57 | 0.37 |
| 6 | 三阶摆振 | 5.700 | 5.69 | 0.18 |
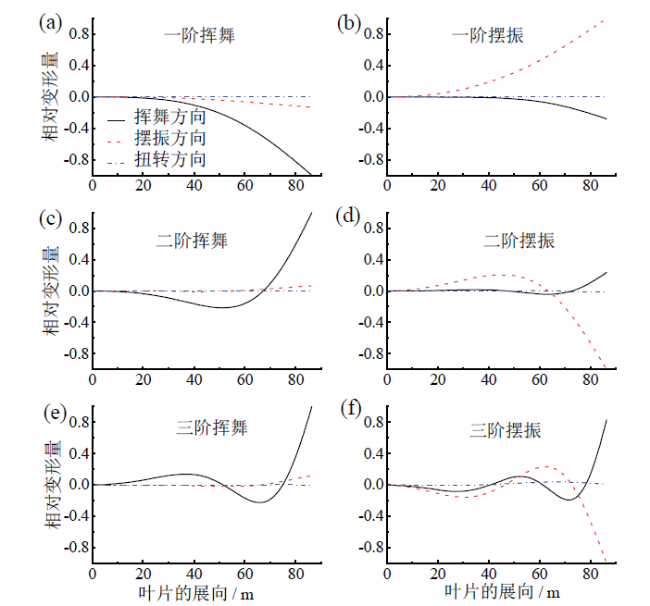
Fig. 5 The first six vibration modes of static blade图5 静止叶片的前六阶振型 |
Table 3 Natural frequency comparison of rotating blade表3 旋转叶片的固有频率对比 |
| 转速 / (r/min) | 固有频率 / Hz | |||||
|---|---|---|---|---|---|---|
| 一阶 | 二阶 | 三阶 | 四阶 | 五阶 | 六阶 | |
| 0.0 | 0.603 | 0.936 | 1.737 | 2.813 | 3.583 | 5.700 |
| 3.0 | 0.608 | 0.938 | 1.741 | 2.815 | 3.587 | 5.705 |
| 6.0 | 0.618 | 0.944 | 1.752 | 2.821 | 3.598 | 5.711 |
| 9.6 | 0.640 | 0.956 | 1.776 | 2.834 | 3.620 | 5.725 |
| 12.0 | 0.658 | 0.969 | 1.793 | 2.845 | 3.638 | 5.737 |
| 15.0 | 0.688 | 0.983 | 1.828 | 2.865 | 3.672 | 5.762 |
| 19.2 | 0.737 | 1.012 | 1.885 | 2.897 | 3.728 | 5.797 |
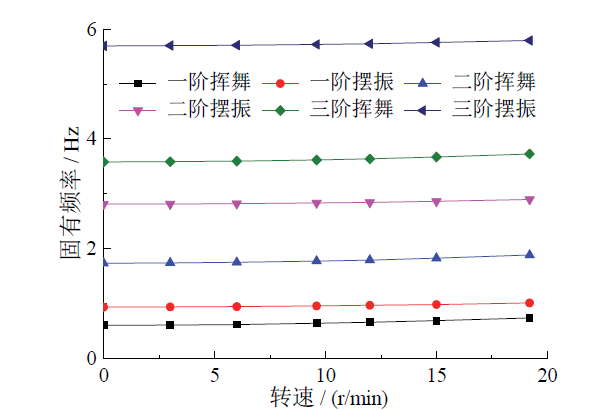
Fig. 6 Natural frequency comparison of rotating blade图6 旋转叶片的固有频率对比 |
4 结论
基于几何精确梁理论,结合广义-α时间预测法,建立梁的几何非线性动力学模型,并通过不同的算例验证了该模型对描述非线性大变形及动力学特性的准确性。然后在此模型的基础上,加入10 MW风力机的数据,考虑叶片复合铺层材料的各向异性特性,建立大型风力机叶片的非线性动力学模型,将叶片非线性动力学模型线性化,对各转速的叶片进行模态分析。通过基于几何精确梁理论对大型风力机叶片的建模及动力学特性分析可得出以下结论：
（1）所建的几何精确梁模型能对柔性梁进行准确的动力学分析。
（2）模型考虑叶片复合铺层材料的各向异性特性,能对大型风力机叶片进行准确的模态分析。
（3）大型风力机叶片随着转速的增大,其动力刚化效应越明显,挥舞方向的动力刚化效应比摆振方向更明显,低阶振型动力刚化效应比高阶振型更明显。
（4）几何精确梁模型能够对大型风力机叶片做非线性大变形及动力学特性分析,且能以较少的自由度对叶片进行计算效率高且准确的动力学特性分析,为叶片非线性振动和气弹耦合响应的研究提供了可行方案。