0 引言
作为一种可再生能源,地热能具有储量丰富、稳定性强、连续性好、利用系数高等优点[1],高效开发利用地热资源将助力我国“双碳”目标的达成。
地热资源的开发利用有诸多方式,其中,同轴套管结构的深井换热技术（deep borehole heat exchanger, DBHE）因不受地域限制且没有回灌问题而备受关注,如图1a所示。DBHE以闭式循环的方式进行地下取热,能够有效保护地下水资源,并且具有适应性强、安全可靠等优点[2,3]。国内外学者已对DBHE的运行特点、换热规律等开展了广泛的研究[4,5,6],DBHE在地热能利用方面具有独特优势,但由于受限于间接换热的方式,取热效率并不高。从青岛某小区DBHE联合热泵供暖系统的测试[7]中看到,当注水流量为30 m3/h时,系统平均取热速率仅为440.67 kW。因此要实现深井换热技术的应用推广,需要对其进行强化换热的研究。增强型地热系统（enhanced geothermal systems, EGS）是目前开发干热岩资源的有效技术手段[8],EGS将循环流体注入人工压裂热储中,与高温岩体接触换热后采出,传统EGS项目在工程实施过程存在循环流体损失大、压裂体积大、投资成本高、诱发地质破坏等问题[9]。
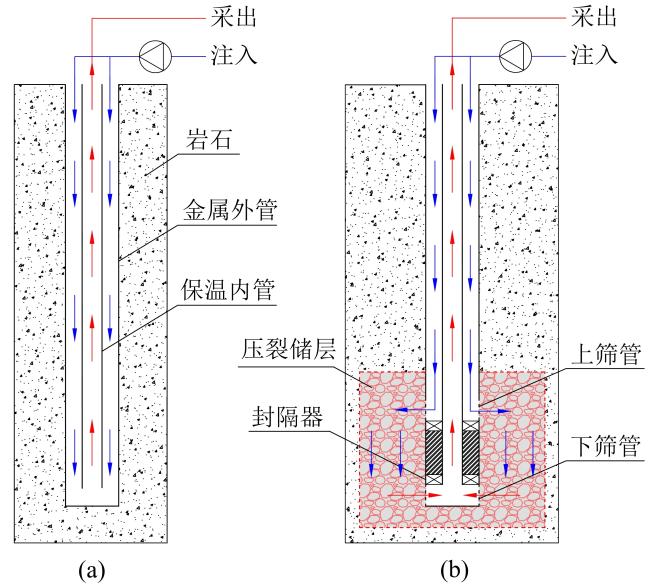
Fig. 1 Schematic diagram of DBHE (a) and SEGS (b)图 1 DBHE（a）和SEGS（b）示意图 |
为提高单井系统换热效率,提出一种单井增强型地热系统（single-well enhanced geothermal system, SEGS）,如图1b。SEGS在DBHE基础上,借鉴了干热岩的开发思路,对单井底部岩体进行小范围压裂改造,在一定程度上避免了由于双井或多井EGS系统大体积压裂带来的投资成本高、流体损失大的问题。同时,相对于闭式单井套管系统,将间接换热改变为接触换热,以提高换热效率。使用超临界CO2作为SEGS的循环流体,超临界状态的CO2经外管进入压裂岩体,与高温岩石进行接触换热后由中心管采出。与水相比,超临界CO2具有低黏度、高膨胀性等特点[10],使用CO2进行地热开发除了具有减小循环能耗、避免管道结垢的优点,还具有“储碳”的附加效益[11,12]。相对目前的单井套管系统和EGS,SEGS兼顾了经济性能和换热效率。
SEGS的结构、流体循环路径等均与双井或多井EGS有很大区别,关于以CO2为循环工质的单井增强地热系统（CO2-SEGS）流动换热规律以及取热性能的研究鲜有报道。本文考虑CO2可压缩性以及井纵向压力传递特性,建立SEGS井筒流动换热和储层热-流-固耦合的数学模型,获得CO2-SEGS性能变化曲线,分析水和CO2在SEGS中取热效果的差异,研究封隔间距、中心管保温对系统换热的影响。
1 数学模型
1.1 模型假设
假设岩石为均质各向同性体,其物性参数包括热导率、比热、密度等保持恒定;流体流动服从达西定律;岩石和流体的换热满足局部热平衡假设,忽略固液两相温差;岩石形变受热应力和孔隙压力的影响,符合线弹性模型[13]。CO2的密度、比热容、黏度、比焓、导热率等物性参数调用美国国家标准与技术研究院（National Institute of Standards and Technology, NIST）数据库。
1.2 数学方程
1.2.1 井筒流动换热模型
井筒流体质量守恒方程与动量守恒方程为：
$\frac{\partial \left( {{A}_{\text{p}}}{{\rho }_{\text{f}}} \right)}{\partial t}+\nabla \cdot \left( {{A}_{\text{p}}}{{\rho }_{\text{f}}}{{u}_{\text{f}}} \right)=0$ (1)
${{\rho }_{\text{f}}}\frac{\partial {{u}_{\text{f}}}}{\partial t}=-\nabla p-\frac{1}{2}{{f}_{\text{D}}}\frac{{{\rho }_{\text{f}}}}{{{d}_{\text{p}}}}|{{u}_{\text{f}}}|{{u}_{\text{f}}}-{{\rho }_{\text{f}}}g$ (2)
fD为摩擦系数,由Haaland模型[14]计算得出：
$\frac{1}{\sqrt{{{f}_{\text{D}}}}}=-1.8\lg \left[ {{\left( \frac{\text{0}\text{.046}}{3.7{{d}_{\text{p}}}} \right)}^{1.11}}+\frac{6.9}{Re} \right]$ (3)
中心管和环空管的流体能量守恒方程为：
$\begin{align} & {{\rho }_{\text{f}}}{{A}_{\text{p}}}{{c}_{p\text{,f}}}\frac{\partial T}{\partial t}+{{\rho }_{\text{f}}}{{A}_{\text{p}}}{{c}_{p\text{,f}}}{{u}_{\text{f}}}\cdot \nabla T=\nabla \cdot \left( {{A}_{\text{p}}}{{\lambda }_{\text{f}}}\nabla T \right)+ \\ & \frac{1}{2}{{f}_{\text{D}}}\frac{{{\rho }_{\text{f}}}{{A}_{\text{p}}}}{{{d}_{\text{h}}}}|{{u}_{\text{f}}}|{{u}_{\text{f}}}^{2}\text{+}{{q}_{\text{s}}}T-{{Q}_{1}} \end{align}$ (4)
$\begin{matrix} {{\rho }_{\text{f}}}{{A}_{\text{p}}}{{c}_{p\text{,f}}}\frac{\partial T}{\partial t}+{{\rho }_{\text{f}}}{{A}_{\text{p}}}{{c}_{p\text{,f}}}{{u}_{\text{f}}}\cdot \nabla T=\nabla \cdot \left( {{A}_{\text{p}}}{{\lambda }_{\text{f}}}\nabla T \right)+ \\ \frac{1}{2}{{f}_{\text{D}}}\frac{{{\rho }_{\text{f}}}{{A}_{\text{p}}}}{{{d}_{\text{p}}}}|{{u}_{\text{f}}}|{{u}_{\text{f}}}^{2}+{{q}_{\text{s}}}T+{{Q}_{1}}+{{Q}_{2}} \\ \end{matrix}$ (5)
${{q}_{\text{s}}}\text{=}-{{\left. \frac{{{A}_{\text{p}}}}{\rho }\frac{\partial \rho }{\partial T} \right|}_{\text{p}}}\left( \frac{\partial p}{\partial t}+{{u}_{\text{f}}}\cdot \nabla p \right)$ (6)
中心管流体的热传递项Q1由下式表示：
${{Q}_{\mathrm{1}}}=\frac{{{T}_{\mathsf{f2}}}-{{T}_{\mathrm{f1}}}}{{{R}_{\mathsf{1}}}}$ (7)
${{R}_{\mathrm{1}}}=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }{{r}_{\mathrm{1}}}{{h}_{\text{1}}}}+\frac{\ln \left( {{r}_{2}}/{{r}_{1}} \right)}{2\text{ }\!\!\pi\!\!\text{ }{{\lambda }_{1}}}+\frac{1}{2\text{ }\!\!\pi\!\!\text{ }{{r}_{2}}{{h}_{\text{2}}}}$ (8)
环空管流体的热传递项Q2由下式表示：
${{Q}_{\mathrm{2}}}=\frac{{{T}_{\mathrm{f1}}}-{{T}_{\mathrm{f2}}}}{{{R}_{\mathrm{1}}}}+\frac{{{T}_{\text{r}}}-{{T}_{\mathrm{f2}}}}{{{R}_{\mathrm{2}}}}$ (9)
${{R}_{2}}=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }{{r}_{3}}{{h}_{\text{3}}}}+\frac{\ln \left( {{r}_{4}}/{{r}_{3}} \right)}{2\text{ }\!\!\pi\!\!\text{ }{{\lambda }_{\mathrm{2}}}}$ (10)
$h=\frac{Nu\cdot {{\lambda }_{\mathrm{f}}}}{d\text{p}}$ (11)
$Nu=\frac{\left( {{f}_{\text{D}}}/8 \right)\cdot \left( Re-1000 \right)\cdot Pr}{1+12.7\sqrt{{{f}_{\text{D}}}/8}\left( P{{r}^{\mathrm{2/3}}}-1 \right)}$ (12)
1.2.2 储层流动换热模型
储层岩石和裂隙热交换的能量守恒方程为：
${{\left( \rho {{c}_{p}} \right)}_{\mathrm{eff}}}\frac{\partial T}{\partial t}+{{\rho }_{\mathrm{f}}}{{c}_{p\text{,f}}}{{u}_{\text{f}}}\cdot \nabla T-\nabla \cdot \left( {{\lambda }_{\mathrm{eff}}}\nabla T \right)=-{{Q}_{\mathrm{r}}}$ (13)
${{d}_{\mathrm{f}}}{{\left( \rho {{c}_{p}} \right)}_{\mathrm{eff}}}\frac{\partial T}{\partial t}+{{d}_{\mathrm{f}}}{{\rho }_{\mathrm{f}}}{{c}_{p\text{,f}}}{{u}_{\text{f}}}\cdot \nabla T-\nabla \cdot \left( {{d}_{\mathrm{f}}}{{\lambda }_{\mathrm{eff}}}\nabla T \right)={{d}_{\mathrm{f}}}{{Q}_{\mathrm{r}}}$(14)
(ρcp)eff和λeff为有效比热容和有效导热系数,表示为：
${{\left( \rho {{c}_{p}} \right)}_{\text{e}\mathrm{ff}}}=\left( 1-\varphi \right){{\rho }_{\text{r}}}{{c}_{p\text{,r}}}+\varphi {{\rho }_{\mathrm{f}}}{{c}_{p\text{,f}}}$ (15)
${{\lambda }_{\mathrm{eff}}}=\left( 1-\varphi \right){{\lambda }_{\text{r}}}+\varphi {{\lambda }_{\mathrm{f}}}$ (16)
储层中流体流动由达西定律和质量守恒方程表示：
${{\rho }_{\mathrm{f}}}S\frac{\partial p}{\partial t}-\nabla \cdot {{\rho }_{\mathrm{f}}}\left[ \frac{{{k}_{\text{r}}}}{{{\eta }_{\mathrm{f}}}}\left( \nabla p+{{\rho }_{\mathrm{f}}}g\nabla z \right) \right]=-{{\rho }_{\mathrm{f}}}{{\alpha }_{\mathrm{B}}}\frac{\partial e}{\partial t}-{{Q}_{\mathrm{f}}}$ (17)
${{d}_{\mathrm{f}}}{{\rho }_{\mathrm{f}}}S\frac{\partial p}{\partial t}-\nabla \cdot {{d}_{\mathrm{f}}}{{\rho }_{\mathrm{f}}}\left[ \frac{{{k}_{\mathrm{f}}}}{{{\eta }_{\mathrm{f}}}}\left( \nabla p+{{\rho }_{\mathrm{f}}}g\nabla z \right) \right]=-{{d}_{\mathrm{f}}}{{\rho }_{\mathrm{f}}}{{\alpha }_{\mathrm{B}}}\frac{\partial e}{\partial t}+{{d}_{\mathrm{f}}}{{Q}_{\mathrm{f}}}$ (18)
其中：
${{\alpha }_{\text{B}}}=1-\frac{{{K}_{\text{d}}}}{{{K}_{\text{s}}}}$ (19)
$S=\varphi {{\chi }_{\text{f}}}+\left( {{\alpha }_{\text{B}}}-\varphi \right)\frac{1-{{\alpha }_{\text{B}}}}{{{K}_{\text{d}}}}$ (20)
储层岩石变形的力学平衡方程[15]为：
$\begin{align} & \mu {{u}_{\mathrm{i,jj}}}+\left( \lambda +\mu \right){{u}_{\mathrm{j,ji}}}- \\ & {{\alpha }_{\text{B}}}{{p}_{\text{i}}}-3{{K}_{\mathrm{d}}}{{\alpha }_{\mathrm{T}}}\Delta T+{{F}_{\mathrm{i}}}=0 \\ \end{align}$ (21)
$\lambda =\frac{Ev}{\left( 1+v \right)\left( 1-2v \right)},\text{ }\mu =\frac{E}{2\left( 1+v \right)}$ (22)
${{K}_{\text{d}}}=\frac{E}{3\left( 1-2v \right)}$ (23)
岩石变形会改变裂缝的孔径,从而导致裂缝渗透率发生变化,应力和裂隙渗透率之间的关系表示为：
${{k}_{\mathrm{f}}}={{k}_{\mathrm{f0}}}\exp \left( -\sigma _{\mathrm{n}}^{\prime }/{{\sigma }^{*}} \right)$ (24)
式中：σ* 为标准化常数,取值 -10 MPa[16]。
1.3 模型验证
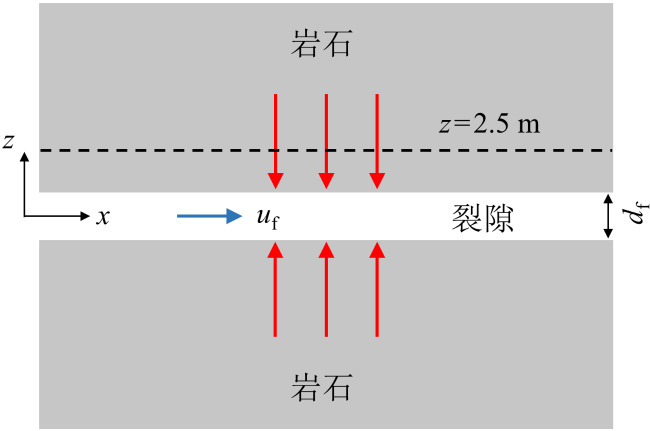
Fig. 2 Schematic diagram of physical model of fracture图 2 裂隙流动换热物理模型示意图 |
裂隙中的温度分布表示为：
$\begin{align} & {{T}_{\text{f}}}\left( x,t \right)={{T}_{\text{0}}}+\left( {{T}_{\text{i}}}-{{T}_{\text{0}}} \right)\times \\ & \text{erfc}\left( \frac{{{\lambda }_{\text{r}}}x}{{{\rho }_{\text{f}}}{{c}_{p\text{,f}}}{{u}_{\text{i}}}{{d}_{\text{f}}}}\sqrt{\frac{{{\rho }_{\text{r}}}{{c}_{p\text{,r}}}{{u}_{\text{i}}}}{{{\lambda }_{\text{r}}}\left( {{u}_{\text{i}}}t+x \right)}} \right) \\ \end{align}$ (25)
岩石基质中的温度分布表示为：
$\begin{align} & {{T}_{\text{r}}}\left( x,z,t \right)={{T}_{\text{0}}}+\left( {{T}_{\text{i}}}-{{T}_{\text{0}}} \right)\times \\ & \text{erfc}\left( \frac{2{{\lambda }_{\text{r}}}x+|z|{{\rho }_{\text{f}}}{{c}_{p\text{,f}}}{{u}_{\text{i}}}{{d}_{\text{f}}}}{2{{\rho }_{\text{f}}}{{c}_{p\text{,f}}}{{u}_{\text{i}}}{{d}_{\text{f}}}}\sqrt{\frac{{{\rho }_{\text{r}}}{{c}_{p\text{,r}}}{{u}_{\text{i}}}}{{{\lambda }_{\text{r}}}\left( {{u}_{\text{i}}}t+x \right)}} \right) \\ \end{align}$ (26)
式中：下标f和r分别表示水和岩石;x和z为位置坐标;erfc表示互补误差函数。
Table 1 Calculation parameters of the fracture model表1 裂隙流动换热模型计算参数 |
| 参数 | 数值 |
|---|---|
| 岩石密度 / (kg/m3) | 2 700 |
| 岩石比热 / [J/(kg∙℃)] | 1 000 |
| 岩石导热系数 / [W/(m∙℃)] | 2.8 |
| 裂隙孔径 / m | 0.001 |
| 注射速度 / (m/s) | 0.01 |
| 初始温度 / ℃ | 80 |
| 注入温度 / ℃ | 30 |
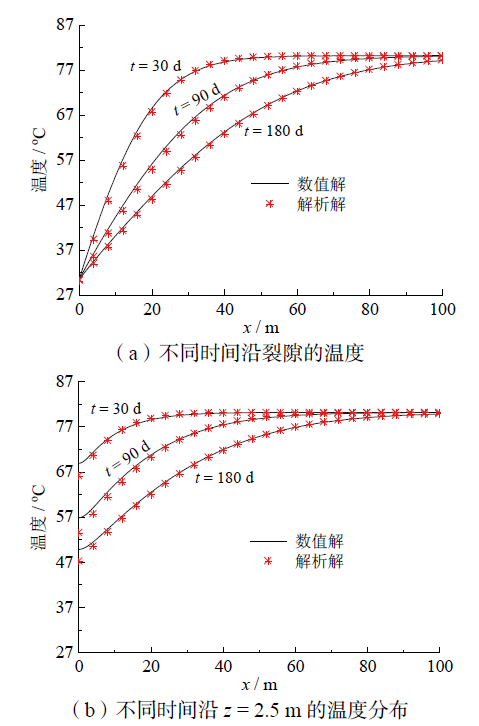
Fig. 3 Comparison of analytical solution and numerical solution图 3 裂隙流动换热问题解析解与数值解比较 |
2 物理模型
2.1 几何模型
计算模型如图4所示。该模型由围岩、井筒、压裂储层组成。主井筒采用同轴套管结构,水经环空管由上部筛管注入压裂储层,经下部筛管从中心管采出。主井筒长度为3 000 m,底部为开式结构,上下筛管长度均为50 m,间距为300 m。环空管和中心管均由一维直线表示,流动传热采用一维模型。井筒外部岩石半径为250 m。压裂区域半径150 m,位于地下3 000 ~ 3 500 m处,内部分布有离散裂隙。假定裂隙形状为二维圆盘,不考虑其粗糙度和起伏度,裂隙面中心点的位置服从研究域内的随机分布[19]。将井筒底部温度、压力与储层筛管的温度、压力进行耦合求解。井筒参数、储层岩石裂隙参数和裂隙网络参数分别列于表2、表3[20]和表4。
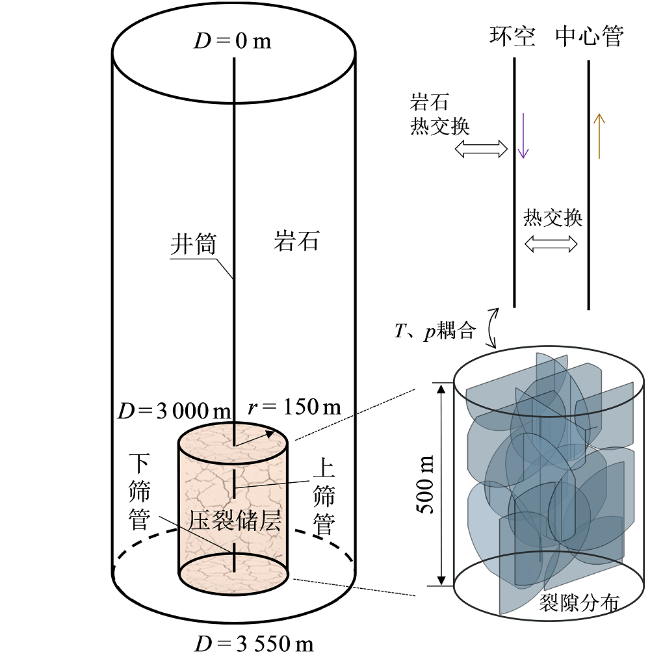
Fig. 4 Schematic diagram of the model图 4 模型示意图 |
Table 2 Parameters of the well tube表2 井筒参数 |
| 项目 | 外径 / m | 内径 / m | 导热系数 / [W/(m∙℃)] |
|---|---|---|---|
| 外管 | 0.38 | 0.34 | 45.0 |
| 保温管 | 0.22 | 0.19 | 0.1 |
Table 3 Parameters of reservoir rocks and fractures表3 储层岩石和裂隙参数 |
| 参数 | 压裂储层 | 围岩 | 裂隙 |
|---|---|---|---|
| 密度 / (kg/m3) | 2 590 | 2 623 | 2 000 |
| 比热 / [J/(kg∙℃)] | 980 | 1 000 | 800 |
| 导热系数 / [W/(m∙℃)] | 2.8 | 3 | 2.8 |
| 渗透率 / m2 | 7 × 10-15 | 1 × 10-18 | 1 × 10-11（kf0） |
| 孔隙度 | 0.07 | 0.01 | 1 |
| 弹性模量 / GPa | 30 | 30 | 30 |
| 泊松比 | 0.25 | 0.25 | 0.25 |
| 热膨胀系数 | 5 × 10-6 | 5 × 10-6 | 5 × 10-6 |
| Biot系数 | 0.7 | 0.7 | 0.7 |
Table 4 Parameters of the fracture network表 4 裂隙网络参数 |
| 组别 | 个数 | 倾向 / ° | 倾角 / ° | 轴长 / m | 标准差 | 开度 / mm |
|---|---|---|---|---|---|---|
| 1 | 10 | 90 | 90 | 100 | 0 | 1 |
| 2 | 5 | 0 | 90 | 100 | 0 | 1 |
2.2 初始条件及边界条件
初始条件下,地表温度为20℃,温度梯度为0.05℃/m。储层顶部边界孔隙压力为30 MPa,压力梯度为5 000 Pa/m。初始状态下储层和井筒内的CO2都处于超临界状态,环空管注入温度为40℃,额定循环流量为30 kg/s,中心管出口流量与环空管循环流量相等。绝热和无流动边界条件应用于所有外部边界。上部筛管的注入温度和压力由井筒模型计算赋值,中心管底部的温度和压力由储层模型计算赋值。
2.3 有限元求解设置
采用有限元求解器求解偏微分方程。使用1D模型描述环空和内管中的热传递,使用3D模型模拟周围地层中的热过程,通过特定的耦合算子将变量从源域映射到不同维度的目标域来实现耦合项的计算。采用全耦合算法求解整个模型,相对容差设为1 × 10-5,作为数值计算的收敛准则。采用自适应时间步进自动调整时间步长以保持所需的相对容差,最大步长约束设置为1 d。为保证数值结果独立于网格数,选取第20年的采出温度进行网格无关化验证。从图5可以看出,当模型的网格数超过98 532时,出口温度将基本保持不变。考虑到模型精度和计算时间,在后续研究中采用133 604的网格数进行计算。
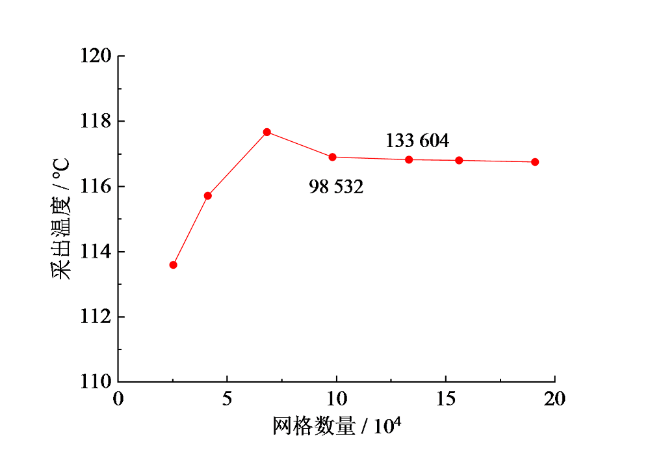
Fig. 5 Numerical results with different mesh numbers图5 不同网格数下的数值结果 |
图6为地下3 075 m处以井筒为中心周围岩石的径向温度分布,该位置的温度分布可显示系统最大温度影响范围。随着时间推移,温度影响的径向范围变大,第20年时温度扰动未到达边界处,说明求解区域的选择是合理的。
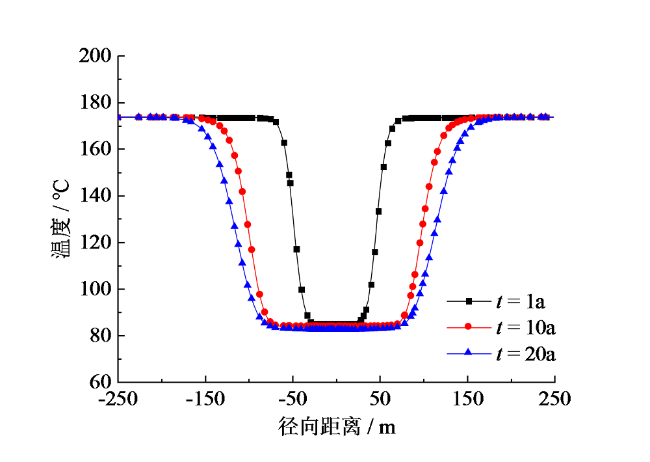
Fig. 6 Radial temperature distribution of the reservoir图6 储层径向温度分布 |
3 结果与分析
3.1 CO2-SEGS取热性能分析
图7为SEGS不同位置处的CO2温度随时间的变化情况。在20年的生产过程中,环空管井底CO2温度稳定在83℃左右,该温度也为CO2进入储层时的温度。中心管井口CO2温度与中心管井底CO2温度变化趋势一致,随着时间推移,两者都出现一定程度衰减,中心管井底CO2温度从190.96℃降低至170.95℃,中心管井口CO2生产温度从134.09℃降低至116.06℃。中心管井底与中心管井口CO2的温差约为57℃,产生这部分温降的原因,一是由于CO2采出过程中,中心管和环空管之间存在换热,保温管导热系数为0.1 W/(m∙℃),换热量较小;二是由于超临界CO2在注采压差和浮升力驱动下沿井筒向上流动,克服重力做功,损失一部分能量,造成温度降低;三是超临界CO2较大的膨胀系数使其因压力降低迅速膨胀而降温。
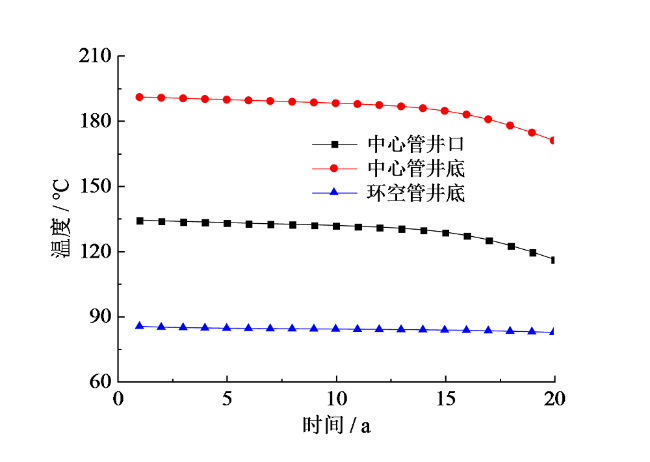
Fig. 7 Temperature evolution at different locations of SEGS图7 SEGS不同位置的温度演变 |
超临界CO2具有强变物性特点,在注入和采出过程中其自身热物理性质如密度、热容等均发生很大变化,如图8所示。可以看到,环空管内CO2比热容和密度均高于中心管,CO2密度变化范围为293.17 ~ 803.12 kg/m3,差值为509.95 kg/m3,这表明由CO2较大的密度差引起的浮力作用可以提供循环动力。
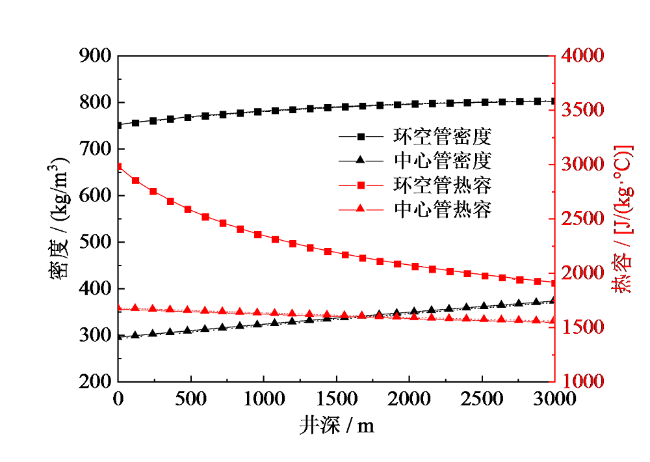
Fig. 8 Thermophysical properties of CO2图8 CO2热物理性质 |
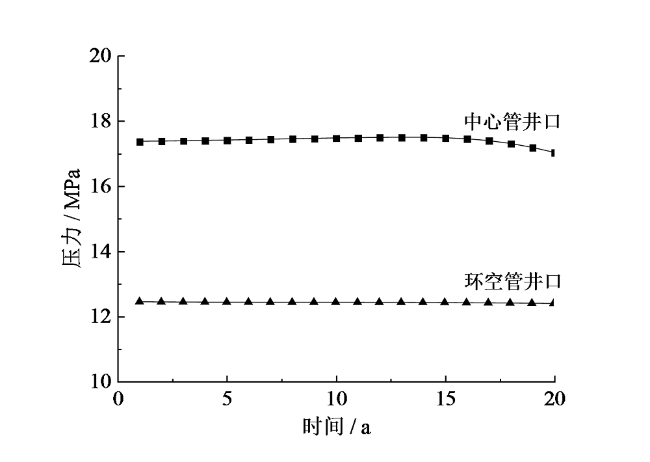
Fig. 9 Evolution of wellhead pressure图9 SEGS井口压力的演变 |
循环流量是地热开发系统的重要运行参数,图10为不同循环流量下系统取热速率的变化情况。增大循环流量有助于提高系统的取热速率,但同时也会导致取热速率衰减幅度变大。20年运行周期内,循环流量为20 kg/s、30 kg/s、40 kg/s和50 kg/s时,年均取热速率分别为3.93 MW、6.25 MW、8.40 MW和10.40 MW,第20年取热速率相对于第1年取热速率衰减幅度分别为3.65%、14.20%、28.62%和37.82%。
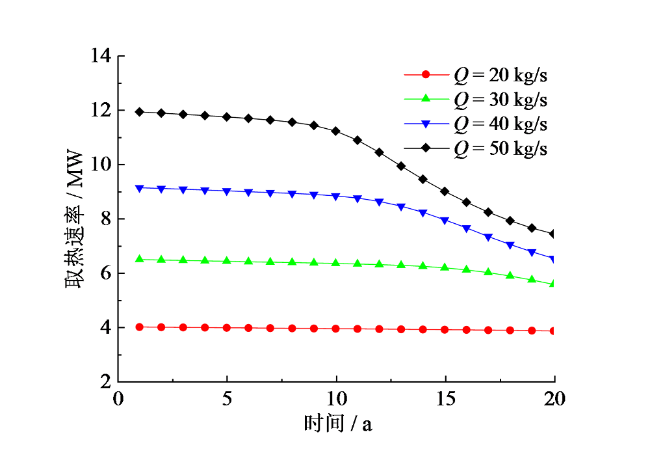
Fig. 10 Heat extraction power of SEGS under different circulating flow rates图10 不同循环流量下SEGS的取热速率 |
随着循环流量的增加,储层间流体的流动需要更大驱动压力。图11为不同流量下环空管井口与中心管井口的压差,可以发现,当循环流量小于52 kg/s时,压差为负,此时SEGS可实现自主循环流动,无需提供额外泵功;当循环流量大于52 kg/s时,压差为正,维持SEGS流体循环将需要额外泵功。从高效稳定取热以及设备配套角度来看,流量控制在30 ~ 40 kg/s是合适的。
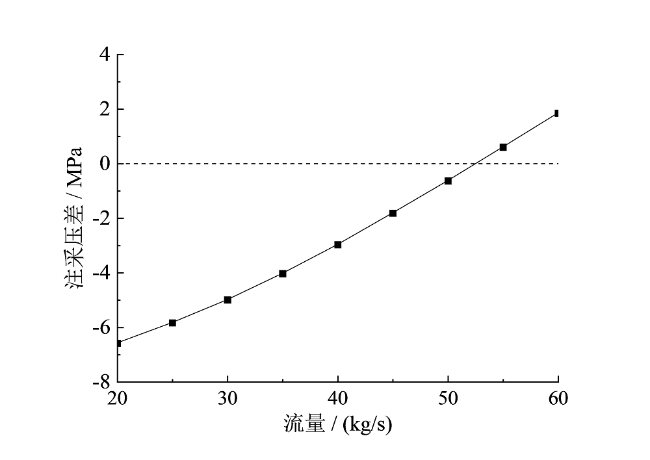
Fig. 11 Relationship between pressure difference and circulating flow图11 注采压差与循环流量的关系 |
3.2 CO2与水取热性能的比较
使用水和CO2作为循环流体,地热系统的取热性能有很大不同。图12为两种流体在不同循环流量下,SEGS运行20年的年均取热速率。由于水的热容比超临界CO2大很多,相同循环流量下,水的取热速率可达到CO2的2.8 ~ 3.2倍。CO2黏度较小,可通过增加循环流量的方式达到与水相同的取热速率。当水的流量为15 kg/s、CO2的流量为40 kg/s时,两者年均取热速率相同,此时可认为CO2和水具有相同的取热能力。
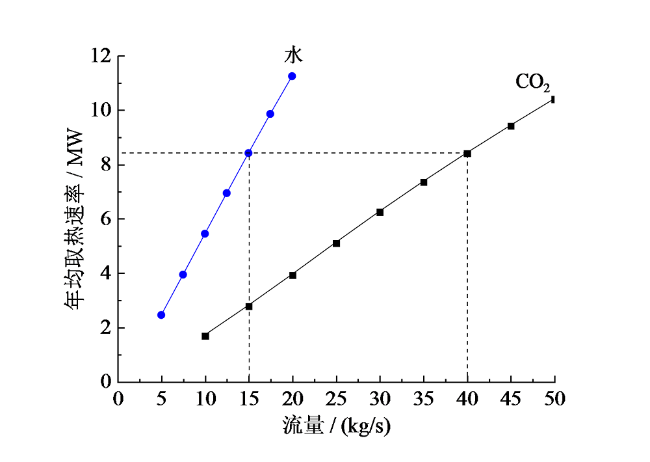
Fig. 12 Average heat extraction power of CO2 and water under different circulating flow rates图12 不同循环流量下CO2和水的平均取热速率 |
对于水和CO2,分别采用15 kg/s和40 kg/s的循环流量,对比了两种系统地热第10年时流体温度沿井深的分布,如图13a所示。对于水-EGS系统,水的比热容、比体积在注采过程中变化较小,温度的变化仅由套管换热所导致,中心管采出温度为173.29℃。对于CO2-EGS系统,由于考虑了压缩性,环空管的温升和中心管的温降均大于水,中心管采出温度为132.30℃,比水低40.99℃。
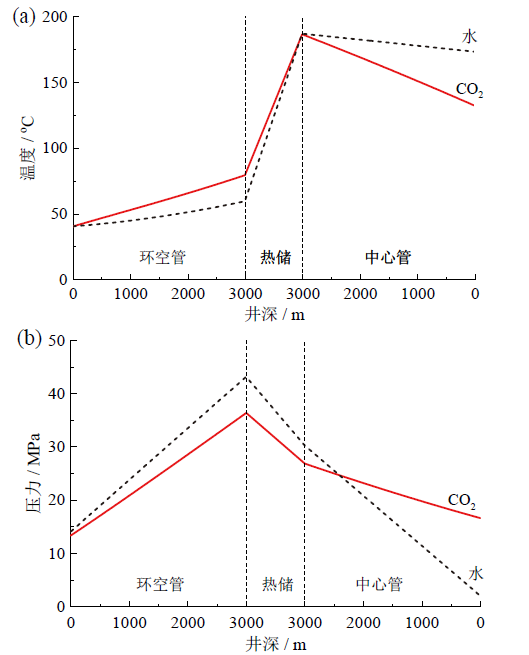
Fig. 13 Distribution of temperature (a) and pressure (b) along well depth图13 温度（a）和压力（b）沿井深分布 |
图13b为两种系统第10年时压力沿井深的分布。对于水-EGS系统,环空管井口压力为14.07 MPa,中心管井口压力为2.02 MPa,热储部分压力损失为12.9 MPa;对于CO2-EGS系统,环空管井口压力为13.34 MPa,中心管井口压力为16.61 MPa,热储部分压力损失为9.50 MPa。CO2不但在热储部分的压力损失更小,而且采出时井口压力远高于水。因此,在取热量相同的情况下,使用CO2作为SEGS的循环流体,系统循环能耗更小。
3.3 影响因素分析
3.3.1 封隔间距的影响
封隔间距是指上下筛管之间的距离。采用CO2作为循环工质,循环流量设定为30 kg/s。保持下筛管位置不变,改变上筛管位置,分析SEGS取热性能的变化。图14为不同封隔间距下中心管出口温度的变化情况。当封隔间距分别为250 m、275 m、300 m、325 m和350 m时,生产温度的年均下降率分别为23.77%、18.67%、13.45%、8.83%和6.28%。
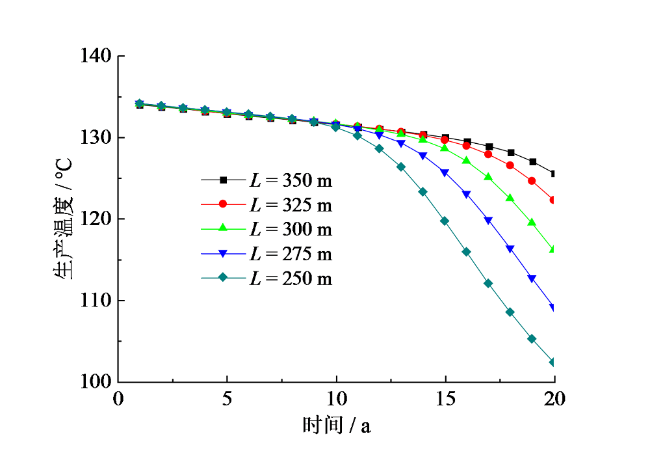
Fig. 14 Production temperature under different packing spacing图14 不同封隔间距下的生产温度 |
图15为不同间距下中心管井口压力变化情况,不同间距下井口压力在生产前期差别不大,而由于考虑了应力作用对裂隙渗透率的影响,前期井口压力有略微上升的趋势,但随着中心管流体温度的降低,其压降逐渐增大,且封隔间距越小,压降越明显。随着封隔间距增大,CO2与岩体的传热面积增大,生产温度衰减速度减小,而传热面积的增大对井口压力的影响较小,因此增大封隔间距对SEGS的取热有利。为保证生产温度稳定,建议封隔间距不小于300 m。封隔间距的大小与压裂岩体建造成本有关系,实际过程中应统筹考虑系统的热力性能和经济性能。
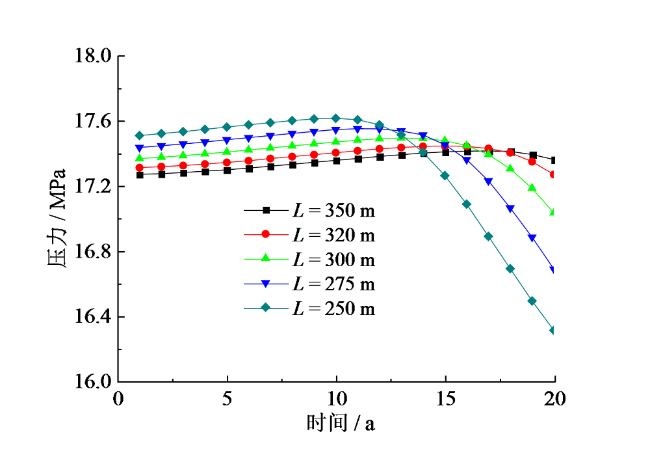
Fig. 15 Wellhead pressure of central pipe under different spacing图15 不同封隔间距下中心管井口压力 |
3.3.2 中心管保温
图16为不同保温管导热系数下中心管出口温度的变化情况,可以发现即使在中心管导热系数为0的情况下,中心管底部与中心管井口也有近42℃的温差,说明CO2上升过程中由于膨胀效应产生的温降在总温降中占比很大。而SEGS的注采都通过一个主井筒进行,中心管流体温度远高于环空管,保温材料的设置对生产温度的影响同样不可小视。图17表示使用不同导热系数的保温管下SEGS年均生产温度和取热速率。随着中心保温管导热系数的增大,年均生产温度和取热速率基本呈现线性降低的趋势,当导热系数从0.05 W/(m∙℃) 增大到0.3 W/(m∙℃)时,年均生产温度降低25.31℃,取热速率降低1.17 MW,导热系数每增大0.05 W/(m∙℃),年均生产温度降低5.06℃,取热速率降低0.234 MW。保温材料的导热系数对SEGS的系统性能具有重要影响,在综合考虑中心保温管价格的前提下,应尽可能采用低导热系数的保温管。
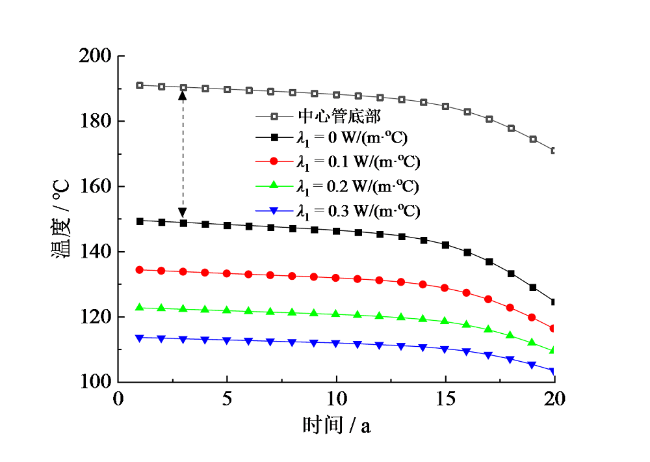
Fig. 16 Temperature variation with time under different thermal conductivity图16 不同导热系数下温度随时间的变化 |
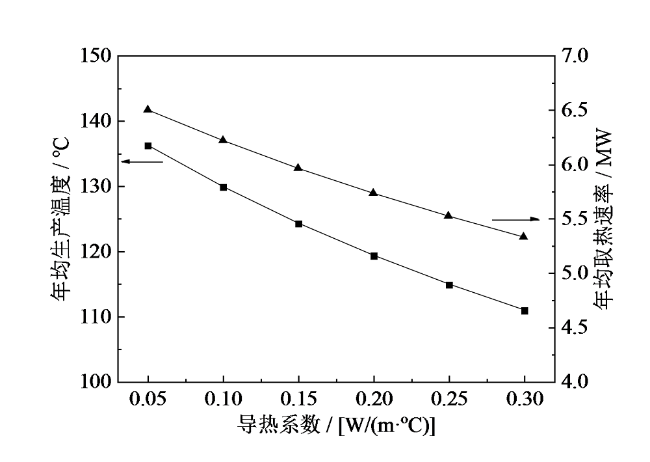
Fig. 17 Average annual production temperature and heat extraction power under different thermal conductivity图17 不同导热系数下的年均生产温度和取热速率 |
4 结论
提出了一种使用CO2作为循环工质的单井增强型地热系统（CO2-SEGS）,建立了井筒-储层耦合的流动换热数学模型,研究了SEGS的系统性能表现,分析了水和CO2在SEGS中取热效果的差异,并对提高SEGS取热性能给出了设计性建议。主要结论如下：
（1）CO2-SEGS可实现储层高效取热,在运行20年的时间中,井口生产温度从134.09℃降低至116.06℃,下降幅度约为13.4%。在采出过程中,CO2密度、热容等均发生很大改变,膨胀效应明显,中心管井口温度比底部温度低约57℃。
（2）当循环流量小于50 kg/s时,CO2-SEGS的采出压力高于注入压力,依靠浮升力作用,SEGS可实现自主循环运行。当流量大于50 kg/s时,注入压力将高于采出压力,维持SEGS流体循环将需要额外泵功。SEGS流量控制在30 ~ 40 kg/s是合适的。
（3）水的流量为15 kg/s、CO2的流量为40 kg/s时,两者年均取热速率相同。CO2的采出温度比水低约41℃,而压力损耗远小于水。在两者取热量相同的情况下,使用CO2作为循环流体比水更具优势。
（4）封隔间距从250 m增大至350 m,温度衰减幅度减小了17.9%。为保证生产温度的稳定,建议封隔间距不小于300 m。中心管保温材料导热系数每增大0.05 W/(m∙℃),年均生产温度降低5.06℃,取热速率降低0.234 MW。SEGS应充分注意中心保温管的设置,避免过大的热量损失。
符号表：
Ap 管道的横截面积,m2
ρf 流体密度,kg/m3
ρr 岩石密度,kg/m3
uf 流速,m/s
t 时间,s
p 压力,Pa
dp 管道水力直径,m
fD 达西摩擦系数
cp,f 流体比热容,J/(m∙℃)
cp,r 岩石比热容,J/(m∙℃)
T 温度,℃
Q1 中心管与环空的热交换,W/m
Q2 环空与周围地层的热交换,W/m
R1 中心管与环空流体之间的热阻,(m∙℃)/W
R2 环空流体与地层之间热阻,(m∙℃)/W
Re 雷诺数
Nu 努塞尔数
Pr 普朗特数
λf 流体导热系数,W/(m∙℃)
λr 岩石导热系数,W/(m∙℃)
λ1 保温内管导热系数,W/(m∙℃)
λ2 外管导热系数,W/(m∙℃)
Qr 岩石基质和裂隙之间的热量传递,W/m3
Tf2 采出管流体温度,℃
Tf1 注入管流体温度,℃
Tr 岩石温度,℃
T0 初始温度,℃
Ti 注入流体的温度,℃
ui 注入流体的流速,m/s
r1、r2 保温管内外半径,m
r3、r4 为金属井壁的内、外半径,m
h 对流传热系数,W/(m2∙℃)
df 裂隙孔径,m
φ 孔隙度
ηf 流体动力黏度,Pa∙s
kr 基质渗透率,m2
kf 裂隙渗透率,m2
kf0 裂隙初始渗透率,m2
αB Biot系数
E 弹性模量,Pa
Qf 基质和裂隙之间的质量传递,kg/(m3∙s)
e 体积应变
ν 泊松比
αT 热膨胀系数
S 存储系数,1/Pa
χf 流体压缩系数,1/Pa
u 位移,m
λ Lamé第一参数,Pa
μ Lamé第二参数,Pa
Ks 固体材料均匀块的体积模量,Pa
Kd 相同材料的多孔基质的排水体积模量,Pa
σ'n 裂隙有效正应力,Pa