0 引言
1 实验装置说明
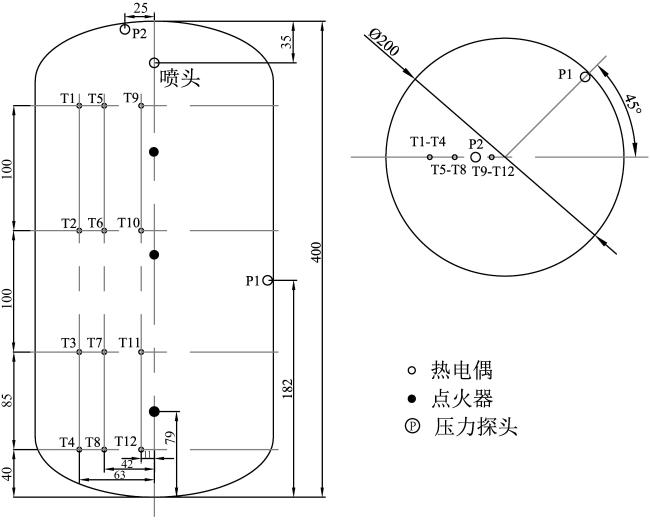
Fig. 1 2D diagram of the experimental device (unit: cm)图1 实验设备二维图(单位:cm) |
Fig. 2 Photo of experiment facility图2 实验装置照片 |
Table 1 Hydrogen experiment instruments and respective parameters表1 氢气实验测量仪表及其参数 |
| 测量参数 | 测量精度 | 探测器 | 测量范围 | 备注 |
|---|---|---|---|---|
| 温度 | ±1.5℃ | 热电偶 | < 1 650℃ | 响应时间 ≈ 0.25s |
| 压强 | 1.6% | 压电传感器 | < 1 MPa | 响应时间 ≤ 1 μs |
| 氢气浓度 | ±3% | 氢气传感器 | 0% ~ 100% | 响应时间 < 0.1 s |
1.1 实验初始条件
1.2 实验气体组成
Table 2 Experiment cases with respective experiment conditions表2 实验工况及其实验条件 |
| 工况 | 氢气浓度 / % | 点火位置 |
|---|---|---|
| H2-I-D-006-1 | 9.96 | 上部 |
| H2-I-D-015-2 | 10.10 | 中部 |
| H2-I-D-024-1 | 9.39 | 下部 |
| H2-I-D-024-3 | 10.27 | 下部 |
1.3 点火位置
2 FLACS 的数值仿真建模
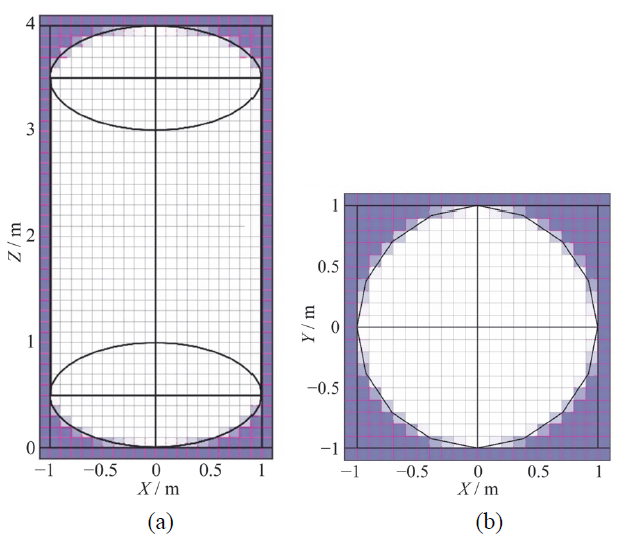
Fig. 3 FLACS code model: (a) XZ section view; (b) XY section view图3 FLACS模型:(a)XZ截面图;(b)XY截面图 |
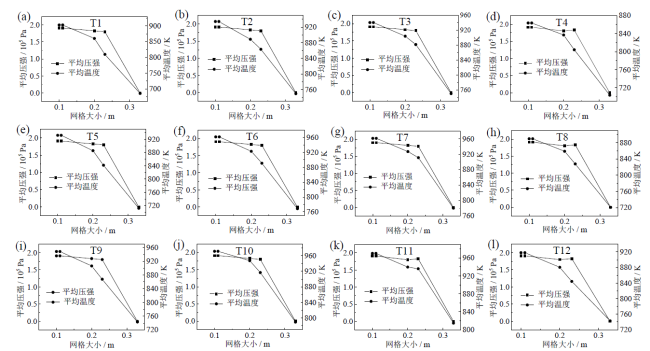
Fig. 4 Average temperature and average pressure profiles generated from hydrogen mixture cloud combustion with various simulation grid sizes in simulation space图4 仿真空间中氢气云燃爆所产生的平均温度以及平均压强随网格大小的变化曲线 |
3 结果与分析
3.1 压强
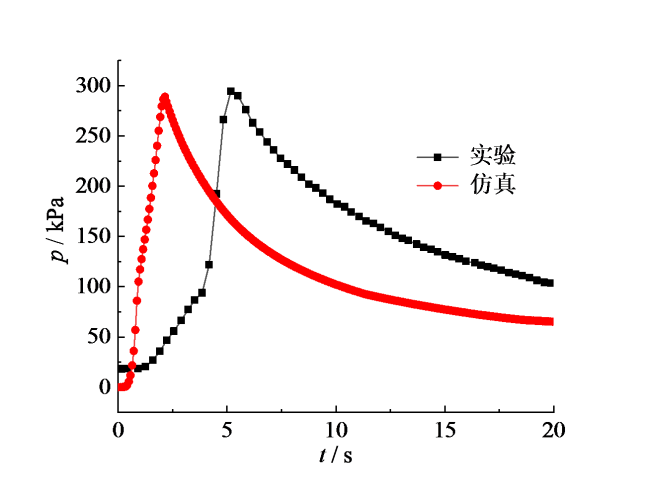
Fig. 5 Comparison of pressure development图5 压强曲线对比图 |
Table 3 Comparison of experiment data with simulation results in each case表3 各工况压强仿真与实验数据对比 |
| 工况 | Pe,max / kPa | Ps,max / kPa | Pe,min / kPa | Ps,min / kPa | Pe,ave / kPa | Ps,ave / kPa | 均值误差比例 / % | 峰值高估比例 |
|---|---|---|---|---|---|---|---|---|
| H2-I-D-024-3 | 325 | 332 | 8.5 | 0 | 165 | 190 | -15.4 | 1.022 |
| H2-I-D-006-1 | 295 | 289 | 8.2 | 0 | 157 | 176 | -11.6 | 0.981 |
| H2-I-D-015-2 | 291 | 324 | 3.5 | 0 | 170 | 194 | -14.3 | 1.113 |
| H2-I-D-024-1 | 263 | 310 | 3.4 | 0 | 151 | 181 | -19.9 | 1.179 |
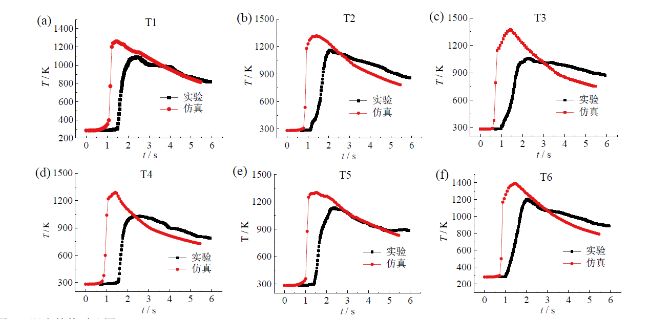
3.2 温度
Fig. 6 Comparison of temperature development图6 温度趋势对比图 |
Table 4 Case H2-I-D-024-3 data表4 H2-I-D-024-3工况数据 |
| 探测点 | Te,max / K | Ts,max / K | Te,min / K | Ts,min / K | Te,ave / K | Ts,ave / K | 均值误差比例 / % | 峰值高估比例 |
|---|---|---|---|---|---|---|---|---|
| T1 | 1 089 | 1 260 | 285 | 284 | 833 | 890 | 7 | 1.16 |
| T2 | 1 162 | 1 326 | 285 | 284 | 895 | 929 | 4 | 1.14 |
| T3 | 1 057 | 1 376 | 285 | 284 | 872 | 938 | 8 | 1.30 |
| T4 | 1 029 | 1 290 | 285 | 284 | 800 | 839 | 5 | 1.25 |
| T5 | 1 135 | 1 300 | 285 | 284 | 859 | 925 | 8 | 1.15 |
| T6 | 1 203 | 1 390 | 285 | 284 | 925 | 964 | 4 | 1.16 |
| T7 | 1 071 | 1 380 | 295 | 284 | 908 | 967 | 7 | 1.29 |
| T8 | 1 006 | 1 300 | 285 | 284 | 757 | 868 | 15 | 1.29 |
| T9 | 1 188 | 1 410 | 285 | 284 | 905 | 958 | 6 | 1.19 |
| T10 | 1 153 | 1 420 | 285 | 284 | 923 | 981 | 6 | 1.23 |
| T11 | 1 026 | 1 366 | 491 | 284 | 843 | 978 | 16 | 1.33 |
| T12 | 998 | 1 300 | 285 | 284 | 726 | 903 | 24 | 1.30 |
Table 5 Case H2-I-D-006-1 data表5 H2-I-D-006-1工况数据 |
| 探测点 | Te,max / K | Ts,max / K | Te,min / K | Ts,min / K | Te,ave / K | Ts,ave / K | 均值误差比例 / % | 峰值高估比例 |
|---|---|---|---|---|---|---|---|---|
| T1 | 1 219 | 1 233 | 299 | 285 | 534 | 428 | 25 | 1.01 |
| T2 | 1 034 | 1 178 | 299 | 285 | 485 | 424 | 14 | 1.14 |
| T3 | 712 | 1 208 | 298 | 285 | 429 | 419 | 2 | 1.70 |
| T4 | 646 | 1 204 | 298 | 285 | 380 | 410 | -7 | 1.86 |
| T5 | 1 249 | 1 241 | 300 | 285 | 561 | 430 | 31 | 0.99 |
| T6 | 1 129 | 1 196 | 300 | 285 | 531 | 426 | 25 | 1.06 |
| T7 | 967 | 1 214 | 299 | 285 | 438 | 420 | 4 | 1.26 |
| T8 | 890 | 1 203 | 298 | 285 | 405 | 411 | -1 | 1.35 |
| T9 | 1 227 | 1 245 | 300 | 285 | 559 | 431 | 29 | 1.01 |
| T10 | 1 027 | 1 224 | 299 | 285 | 503 | 427 | 18 | 1.19 |
| T11 | 1 034 | 1 215 | 299 | 285 | 483 | 421 | 15 | 1.17 |
| T12 | 1 108 | 1 204 | 298 | 285 | 466 | 412 | 13 | 1.09 |
Table 6 Case H2-I-D-015-2 data表6 H2-I-D-015-2工况数据 |
| 探测点 | Te,max / K | Ts,max / K | Te,min / K | Ts,min / K | Te,ave / K | Ts,ave / K | 均值误差比例 / % | 峰值高估比例 |
|---|---|---|---|---|---|---|---|---|
| T1 | 1 116 | 1 300 | 299 | 285 | 517 | 431 | 20 | 1.17 |
| T2 | 1 130 | 1 373 | 300 | 285 | 528 | 431 | 23 | 1.21 |
| T3 | 969 | 1 291 | 299 | 285 | 492 | 427 | 15 | 1.33 |
| T4 | 696 | 1 235 | 299 | 285 | 406 | 423 | -4 | 1.77 |
| T5 | 1 145 | 1 366 | 299 | 285 | 507 | 433 | 17 | 1.19 |
| T6 | 1 116 | 1 396 | 273 | 285 | 515 | 432 | 19 | 1.25 |
| T7 | 1 034 | 1 295 | 273 | 285 | 484 | 428 | 13 | 1.25 |
| T8 | 1 069 | 1 237 | 273 | 285 | 457 | 424 | 8 | 1.16 |
| T9 | 1 116 | 1 426 | 300 | 285 | 520 | 434 | 20 | 1.28 |
| T10 | 1 147 | 1 407 | 273 | 285 | 530 | 434 | 22 | 1.23 |
| T11 | 967 | 1 306 | 273 | 285 | 438 | 429 | 2 | 1.35 |
| T12 | 967 | 1 236 | 273 | 285 | 437 | 425 | 3 | 1.28 |
Table 7 Case H2-I-D-024-1 data表7 H2-I-D-024-1工况数据 |
| 探测点 | Te,max / K | Ts,max / K | Te,min / K | Ts,min / K | Te,ave / K | Ts,ave / K | 均值误差比例 / % | 峰值高估比例 |
|---|---|---|---|---|---|---|---|---|
| T1 | 1 132 | 1 181 | 286 | 285 | 493 | 455 | 8 | 1.04 |
| T2 | 1 173 | 1 244 | 286 | 285 | 530 | 447 | 18 | 1.06 |
| T3 | 1 020 | 1 286 | 273 | 285 | 466 | 445 | 5 | 1.26 |
| T4 | 925 | 1 211 | 273 | 285 | 438 | 440 | 0 | 1.31 |
| T5 | 1 138 | 1 236 | 292 | 285 | 499 | 456 | 9 | 1.09 |
| T6 | 1 203 | 1 311 | 273 | 285 | 536 | 449 | 19 | 1.09 |
| T7 | 403 | 1 291 | 273 | 285 | 302 | 446 | -32 | 3.20 |
| T8 | 882 | 1 214 | 273 | 285 | 397 | 442 | -10 | 1.38 |
| T9 | 1 188 | 1 331 | 284 | 285 | 506 | 458 | 11 | 1.12 |
| T10 | 1 284 | 1 333 | 273 | 285 | 552 | 449 | 23 | 1.04 |
| T11 | 1 181 | 1 274 | 273 | 285 | 529 | 447 | 18 | 1.08 |
| T12 | 948 | 1 217 | 273 | 285 | 418 | 443 | -6 | 1.28 |
Table 8 Error percentage of average temperature and overpredict ratio of average temperature maximum value of each case表8 各工况的温度均值误差和平均温度峰值高估比例 |
| 工况 | 平均误差 / % | 平均高估比例 |
|---|---|---|
| H2-I-D-006-1 | 14.00 | 1.236 |
| H2-I-D-024-1 | 5.25 | 1.289 |
| H2-I-D-015-2 | 13.17 | 1.329 |
| H2-I-D-024-3 | 9.06 | 1.233 |
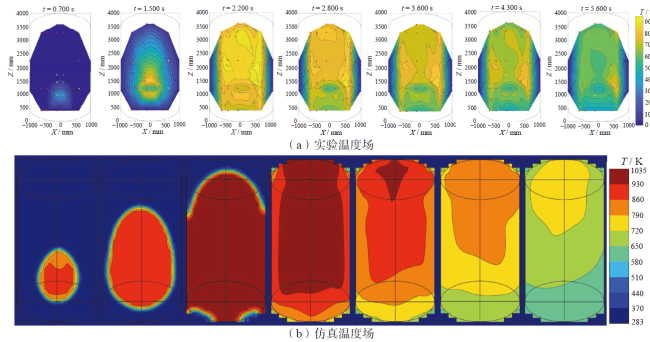
3.3 火焰速度以及温度场的发展趋势
Table 10 Comparison of laminar burning velocities from experiment and simulation表10 实验与仿真的层流火焰燃烧速度对比 |
| 工况 | 利用等效半径估算的层流燃烧速度(R = 1.42 m)/ (m/s) | 利用实际半径估算的层流燃烧速度(R = 1 m)/ (m/s) | 基于热电偶估算的火焰速度 / (m/s) | FLACS仿真计算的燃烧速度(基于压强)/ (m/s) | FLACS仿真计算的燃烧速度(基于温度)/ (m/s) | 仿真值与基于压强的等效半径火焰速度误差 / % | 仿真值与基于压强的实际半径火焰速度误差 / % | 仿真值与基于热电偶估算的火焰速度误差 / % |
|---|---|---|---|---|---|---|---|---|
| H2-I-D-006-1 | 0.30 | 0.21 | 0.54 | 0.175 | 0.175 | 41.67 | 16.67 | 67.59 |
| H2-I-D-015-2 | 0.25 | 0.18 | 0.48 | 0.189 | 0.189 | 24.40 | -5.00 | 60.63 |
| H2-I-D-024-3 | 0.26 | 0.20 | 0.62 | 0.145 | 0.145 | 44.23 | 27.50 | 76.61 |
Fig. 7 Comparison of temperature distribution development图7 温度场的发展趋势对比图 |