0 引言
叶片是风力机发电系统中的两个主要柔性部件之一,其结构性能的优劣将直接影响风力发电机的功率和风能利用率,由于复合材料具有质量轻、耐腐蚀、比强度高及减震性能好等特点[1],采用新型复合材料及合理的铺层优化可有效提高刚度并降低叶片重量,进而降低成本[2],现有大型风力机叶片多采用复合材料铺层制造。国内外学者对风力机复合材料叶片的动态特性开展了许多研究。张立等[3]结合复合材料铺层设计,采用有限元法对复合材料叶片模型进行模态和屈曲分析,得到叶片自重对其结构特性影响。吕计男等[4]建立了复合材料风力机叶片的实体模型,研究了影响叶片频域的因素。刘雄等[5]考虑叶片气动阻尼及旋转产生的离心刚化作用,研究叶片弯曲振动的动力特性,但其将叶片简化为二节点梁单元。李德源等[6]将多体动力学理论与有限元结合起来,研究风力机叶片的振动特性,揭示了动力刚化效应对叶片固有频率的影响规律。周鹏展等[7]采用ANSYS软件对复合材料风力机叶片进行结构分析,结果表明,该叶片的振型以一阶挥舞和一阶摆振为主。BAYOUMY等[8]利用绝对节点坐标公式建立一个三维弹性风力机叶片连续网单元模型,并用六节点板单元对叶片结构进行建模。吕品等[9]采用几何精确梁理论,建立一种用于叶片的非线性单元,计算风力机叶片和整机的频域特性。刘宇航等[10]采用节点位移法分析铺层结构对弯扭耦合叶片整体性能的影响,发现镜像对称铺层结构可实现叶片弯扭耦合。
为此,利用丹麦技术大学（Technical University of Denmark, DTU）所提供的10 MW风力机叶片模型[13],采用绝对节点坐标法,基于一般连续介质力学理论和复合材料本构关系,建立大型风力机旋转复合材料叶片的非线性动力学模型。为了描述叶片的转动,引入大范围转动连体坐标系,结合摄动原理及线性化方法,构建旋转叶片的状态方程,研究叶片在静止与不同转速下的模态振型变化,提供算例验证该模型的正确性,为改进柔性叶片的结构设计提供参考。
1 绝对节点坐标法下的动力学方程
绝对节点坐标法采用连续介质力学理论,通过单元形状函数和节点坐标向量定义梁上任意点的全局坐标向量。
如图1所示,柔性梁单元的所有坐标都建立在全局坐标系下,三维二节点梁单元上的任意一点P对应的绝对位置矢量可以表示为
${{r}_{P}}\left( x,y,z,t \right)=S\left( x,y,z \right)e\left( t \right)$ (1)
式中：$S\left( x,y,z \right)$为梁单元的形状函数矩阵;$\left( x,y,z \right)$为梁单元中任意一点在单元坐标系下的局部坐标;$e$为单元节点的广义坐标矢量。在节点P上包含三个位置矢量和九个位置梯度,通过联立广义坐标矢量与三次插值多项式,获得单元形状函数矩阵[14]。
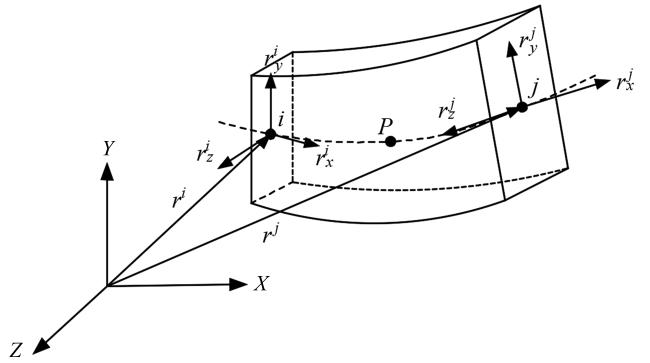
Fig. 1 Three-dimensional beam element model图1 三维梁单元模型 |
1.1 单元质量矩阵
将式（1）对时间$t$求偏导,得到梁单元上任意一点的速度表达式：
$\dot{r}=S\dot{e}$ (2)
通过节点的速度表达式,可计算得到梁单元的动能T：
$T=\frac{1}{2}\int_{V}{{{{\dot{r}}}^{T}}\dot{r}\text{d}V=\frac{1}{2}}{{\dot{e}}^{T}}\left( \int_{V}{\rho {{S}^{T}}S\text{d}V} \right)\dot{e}=\frac{1}{2}{{\dot{e}}^{T}}{{M}_{ele}}\dot{e}$ (3)
式中：$\rho $为梁的材料密度;$V$为梁单元体积;${{M}_{ele}}$为单元常数质量矩阵,其表达式如下
${{M}_{ele}}=\rho \int_{V}{{{S}^{T}}S\text{d}V}$ (4)
1.2 单元刚度矩阵
在一般连续介质力学方法中,任意节点的变形梯度J可由非线性应变-位移关系计算,表达式为
$J=\left( \begin{matrix} {{S}_{1x}}e & {{S}_{1y}}e & {{S}_{1z}}e \\ {{S}_{2x}}e & {{S}_{2y}}e & {{S}_{2z}}e \\ {{S}_{3x}}e & {{S}_{3y}}e & {{S}_{3z}}e \\ \end{matrix} \right)$ (5)
式中：${{S}_{ij}}=\partial {{S}_{i}}/\partial j$,$i=1,2,3$,$j=x,y,z$,表示单元形状函数的第$i$行对坐标$j$求偏导数。
通过变形梯度可计算出梁的格林-拉格朗日应变张量：
$\begin{align} & \varepsilon =\frac{1}{2}\left( {{J}^{T}}J-I \right)=\left[ \begin{matrix} {{\varepsilon }_{11}} & {{\varepsilon }_{12}} & {{\varepsilon }_{13}} \\ {{\varepsilon }_{12}} & {{\varepsilon }_{22}} & {{\varepsilon }_{23}} \\ {{\varepsilon }_{13}} & {{\varepsilon }_{23}} & {{\varepsilon }_{33}} \\ \end{matrix} \right] \\ & =\frac{1}{2}\left( \left[ \begin{matrix} {{e}^{T}}{{S}_{xx}}e & {{e}^{T}}{{S}_{xy}}e & {{e}^{T}}{{S}_{zx}}e \\ {{e}^{T}}{{S}_{xy}}e & {{e}^{T}}{{S}_{yy}}e & {{e}^{T}}{{S}_{yz}}e \\ {{e}^{T}}{{S}_{zx}}e & {{e}^{T}}{{S}_{yz}}e & {{e}^{T}}{{S}_{zz}}e \\ \end{matrix} \right]-I \right) \end{align}$ (6)
式中：${{S}_{ab}}=\sum\limits_{i=1}^{3}{S_{ia}^{T}{{S}_{ib}}}$,$a,b=x,y,z$。
在复合材料本构关系下,应力$\sigma $与应变$\varepsilon $的关系为
$\left[ \begin{matrix} {{\sigma }_{11}} \\ {{\sigma }_{22}} \\ {{\sigma }_{33}} \\ {{\sigma }_{23}} \\ {{\sigma }_{13}} \\ {{\sigma }_{12}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{C}_{11}} & {{C}_{12}} & {{C}_{13}} & 0 & 0 & 0 \\ {{C}_{21}} & {{C}_{22}} & {{C}_{23}} & 0 & 0 & 0 \\ {{C}_{31}} & {{C}_{32}} & {{C}_{33}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{C}_{44}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{C}_{55}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{C}_{66}} \\ \end{matrix} \right]\left[ \begin{matrix} {{\varepsilon }_{11}} \\ {{\varepsilon }_{22}} \\ {{\varepsilon }_{33}} \\ 2{{\varepsilon }_{23}} \\ 2{{\varepsilon }_{13}} \\ 2{{\varepsilon }_{12}} \\ \end{matrix} \right]$ (7)
可简写为
$[\sigma ]=[C][\varepsilon ]$ (8)
式中：$[C]$为正交各向异性材料定义在偏轴坐标系中的弹性系数矩阵,其与正轴坐标系下弹性矩阵的关系为
$[C]=T_{\sigma }^{-1}\bar{C}{{T}_{\varepsilon }}$ (9)
${{T}_{\sigma }}={{\left( T_{\varepsilon }^{T} \right)}^{-1}}$ (10)
式中：$\bar{C}$为正轴坐标系中的弹性矩阵,其各个分量由材料的工程常数计算得到[15];${{T}_{\sigma }}$和${{T}_{\varepsilon }}$分别为偏轴与正轴坐标系之间的应力和应变转换矩阵,其表达式为
${{T}_{\sigma }}=\left[ \begin{matrix} l_{1}^{2} & m_{1}^{2} & n_{1}^{2} & 2{{m}_{1}}{{n}_{1}} & 2{{l}_{1}}{{n}_{1}} & 2{{l}_{1}}{{m}_{1}} \\ l_{2}^{2} & m_{2}^{2} & n_{2}^{2} & 2{{m}_{2}}{{n}_{2}} & 2{{l}_{2}}{{n}_{2}} & 2{{l}_{2}}{{m}_{2}} \\ l_{3}^{2} & m_{3}^{2} & n_{3}^{2} & 2{{m}_{3}}{{n}_{3}} & 2{{l}_{3}}{{n}_{3}} & 2{{l}_{3}}{{m}_{3}} \\ {{l}_{2}}{{l}_{3}} & {{m}_{2}}{{m}_{3}} & {{n}_{2}}{{n}_{3}} & {{m}_{2}}{{n}_{3}}+{{m}_{3}}{{n}_{2}} & {{n}_{2}}{{l}_{3}}+{{n}_{3}}{{l}_{2}} & {{l}_{2}}{{m}_{3}}+{{l}_{3}}{{m}_{2}} \\ {{l}_{1}}{{l}_{3}} & {{m}_{1}}{{m}_{3}} & {{n}_{1}}{{n}_{3}} & {{m}_{1}}{{n}_{3}}+{{m}_{3}}{{n}_{1}} & {{n}_{1}}{{l}_{3}}+{{n}_{3}}{{l}_{1}} & {{l}_{1}}{{m}_{3}}+{{l}_{3}}{{m}_{1}} \\ {{l}_{1}}{{l}_{2}} & {{m}_{1}}{{m}_{2}} & {{n}_{1}}{{n}_{2}} & {{m}_{1}}{{n}_{2}}+{{m}_{2}}{{n}_{1}} & {{n}_{1}}{{l}_{2}}+{{n}_{2}}{{l}_{1}} & {{l}_{1}}{{m}_{2}}+{{l}_{2}}{{m}_{1}} \\ \end{matrix} \right]$(11)
式中：${{l}_{1}},{{l}_{2}},{{l}_{3}}$、${{m}_{1}},{{m}_{2}},{{m}_{3}}$、${{n}_{1}},{{n}_{2}},{{n}_{3}}$是定义在偏轴坐标系与正轴坐标系之间各坐标系的方向余弦,为铺层角$\theta $的函数[15]。
根据应变表达式和应力应变关系式可得到单元应变能为
$\begin{align} & {{U}_{\text{e}}}=\frac{1}{2}\int_{V}{\sigma \varepsilon \text{d}V}=\frac{1}{2}\int_{V}{\left( {{\sigma }_{11}}{{\varepsilon }_{11}}+{{\sigma }_{12}}{{\varepsilon }_{12}}+ \right.} \\ & \left. {{\sigma }_{13}}{{\varepsilon }_{13}}+{{\sigma }_{22}}{{\varepsilon }_{22}}+{{\sigma }_{33}}{{\varepsilon }_{33}} \right)\text{d}V \\ & =\frac{1}{2}\int_{V}{\left( {{C}_{11}}\varepsilon _{11}^{2}+{{C}_{22}}\varepsilon _{22}^{2}+{{C}_{33}}\varepsilon _{33}^{2}+2{{C}_{12}}{{\varepsilon }_{11}}{{\varepsilon }_{22}}+ \right.} \\ & \left. 2{{C}_{13}}{{\varepsilon }_{11}}{{\varepsilon }_{33}}+2{{C}_{23}}{{\varepsilon }_{22}}{{\varepsilon }_{33}}+{{C}_{44}}\varepsilon _{23}^{2}+{{C}_{55}}\varepsilon _{13}^{2}+{{C}_{66}}\varepsilon _{12}^{2} \right)\text{d}V \end{align}$(12)
根据虚功原理,应变能产生的弹性力${{Q}_{k}}$的表达式为
$\begin{align} & {{Q}_{\text{k}}}=-\frac{\partial {{U}_{\text{e}}}}{\partial e}=-\int_{V}{\left[ 2{{C}_{11}}{{\varepsilon }_{11}}+2{{C}_{22}}{{\varepsilon }_{22}}\frac{\partial {{\varepsilon }_{22}}}{\partial e}+ \right.} \\ & 2{{C}_{33}}{{\varepsilon }_{33}}\frac{\partial {{\varepsilon }_{33}}}{\partial e}+2{{C}_{12}}\left( \left. {{\varepsilon }_{11}}\frac{\partial {{\varepsilon }_{22}}}{\partial e}+\frac{\partial {{\varepsilon }_{11}}}{\partial e}{{\varepsilon }_{22}} \right)+ \right. \\ & 2{{C}_{13}}\left( \left. {{\varepsilon }_{11}}\frac{\partial {{\varepsilon }_{33}}}{\partial e}+\frac{\partial {{\varepsilon }_{11}}}{\partial e}{{\varepsilon }_{33}} \right) \right.+2{{C}_{23}}\left( {{\varepsilon }_{22}}\frac{\partial {{\varepsilon }_{33}}}{\partial e}+\frac{\partial {{\varepsilon }_{22}}}{\partial e}{{\varepsilon }_{33}} \right)+ \\ & \left. 2{{C}_{44}}{{\varepsilon }_{23}}\frac{\partial {{\varepsilon }_{23}}}{\partial e}+2{{C}_{55}}{{\varepsilon }_{13}}\frac{\partial {{\varepsilon }_{13}}}{\partial e}+2{{C}_{66}}{{\varepsilon }_{12}}\frac{\partial {{\varepsilon }_{12}}}{\partial e} \right]\text{d}V \\ & =-{{K}_{ele}}(e)e \end{align}$(13)
式中：
$\frac{\partial {{\varepsilon }_{ij}}}{\partial e}=\frac{1}{2}\left( S_{ij}^{T}+{{S}_{ij}} \right)e i,j=1,2,3,j\ge i$ (14)
联立式（5）~ 式（14）,求得单元刚度矩阵${{K}_{ele}}(e)$。
1.3 系统动力学方程
通过对单元质量矩阵${{M}_{ele}}$、单元刚度矩阵${{K}_{ele}}(e)$进行组装,可获得梁模型的广义质量矩阵$M$、广义刚度矩阵$K(e)$。
$\left\{ \begin{matrix} M={{B}^{T}}{{M}_{ele}}B \\ K(e)={{B}^{T}}{{K}_{ele}}(e)B \\ {{Q}_{e}}={{B}^{T}}{{Q}_{ele}} \\ \end{matrix} \right.$ (15)
式中：$B$是$m\times n$维的组装布尔矩阵,$m$为梁单元坐标数与单元数目的乘积,$n$为节点坐标数;${{Q}_{e}}$为广义力矩阵。
绝对节点坐标下三维旋转梁的动力学方程为
$M\ddot{e}+K(e)e={{Q}_{e}}$ (16)
2 风力机叶片非线性动力学建模
2.1 叶片建模及材料铺层设计
Table 1 Fiber orientation and apparent mechanical properties of the multidirectional plies表1 多向层板的纤维方向和力学性能 |
| 力学性能 | 单轴向布 | 双轴向布 | 三轴向布 |
|---|---|---|---|
| 纤维体积含量 | 0.55 | 0.5 | 0.5 |
| 单层向板 | 层板2 | 层板1 | 层板1 |
| 0° 方向纤维 / % | 95 | 0 | 30 |
| 90° 方向纤维 / % | 5 | 0 | 0 |
| +45° 方向纤维 / % | 0 | 50 | 35 |
| -45° 方向纤维 / % | 0 | 50 | 35 |
| 弹性模量E1 / Gpa | 41.63 | 13.92 | 24.79 |
| 弹性模量E2 / Gpa | 14.93 | 13.92 | 14.67 |
| 泊松比 | 0.241 | 0.533 | 0.478 |
| 剪切模量G12 / Gpa | 5.047 | 11.50 | 9.413 |
| 剪切模量${{G}_{13}}={{G}_{23}}$ / Gpa | 5.046 98 | 4.538 64 | 4.538 64 |
| 密度$\rho $/ (kg/m3) | 1 914.5 | 1 845.0 | 1 845.0 |
2.2 叶片翼型截面信息处理
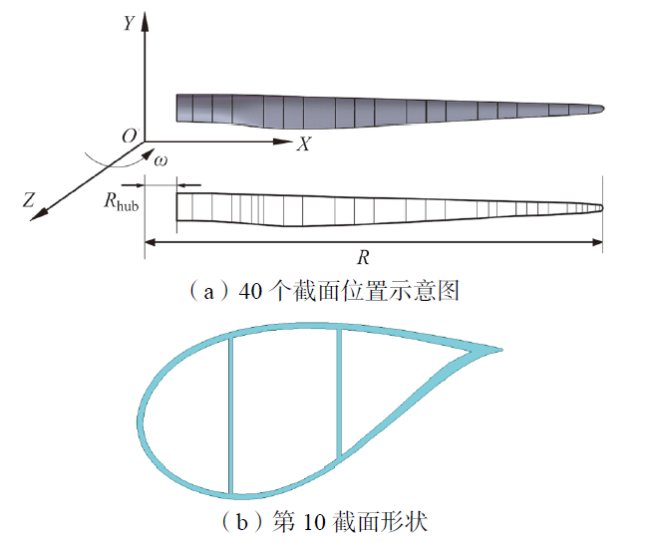
Fig. 2 Schematic diagram of blade section position图2 叶片截面位置及形状 |
Table 2 Part of the element information of section 10表2 第10截面部分单元信息 |
| 单元号 | 所属材料 | 单元节点序号 | 单元面积 / m2 | ||
|---|---|---|---|---|---|
| 1 | 层板1 | 2 | 14 | 8 | 1.157 × 10-4 |
| 2 | 层板1 | 2 | 7 | 14 | 1.154 × 10-4 |
| 3 | 层板1 | 7 | 13 | 14 | 1.160 × 10-4 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 12 | 巴沙木 | 10 | 3 | 1 | 1.139 × 10-4 |
| 13 | 巴沙木 | 16 | 28 | 22 | 3.046 × 10-5 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
Table 3 Part of the node information of section 10表3 第10截面部分节点信息 |
| 节点号 | Y方向 / m | Z方向 / m | 夹角 / ° |
|---|---|---|---|
| 1 | 0.644 | -2.567 | 1.290 |
| 2 | 0.608 | -2.579 | 1.290 |
| 3 | 0.424 | -2.625 | 1.355 |
| ︙ | ︙ | ︙ | ︙ |
| 115 | 1.635 | -1.871 | 0.739 |
| 116 | 1.687 | -1.819 | 0.711 |
| ︙ | ︙ | ︙ | ︙ |
$\int_{0}^{1}{\int_{0}^{1-{{\lambda }_{1}}}{f\left( {{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}} \right)\text{d}{{\lambda }_{2}}\text{d}{{\lambda }_{1}}=\sum\limits_{k=1}^{n}{f\left( \lambda _{1}^{k},\lambda _{2}^{k},\lambda _{3}^{k} \right){{\omega }_{k}}}}}$ (17)
式中：$n$为积分点个数;${{\lambda }_{i}}(i=1,2,3)$为三角形单元中某积分点a的面积坐标;$\lambda _{i}^{k}(i=1,2,3)$为面积坐标的Hammer求积点;${{\omega }_{k}}$为对应权系数。
在叶片单元展向方向使用高斯积分求解,其积分形式一般如下
$\int_{-1}^{1}{f(\xi )}\text{d}\xi =\sum\limits_{i=1}^{n}{{{\omega }_{i}}}f({{\xi }_{i}})$ (18)
式中：积分区域需转换到标准区域$[-1,1]$;$\xi $为标准化坐标;$f(\xi )$为被积函数;$n$为积分点个数;${{\xi }_{i}}$为积分点;${{\omega }_{i}}$为对应权系数。
2.3 旋转动力学方程的建立
为了描述叶片的转动,引入大范围浮动坐标系,建立关于浮动坐标系下的动力学方程,绝对坐标需要用新的坐标向量来表示。
令$\tilde{e}$为浮动坐标系上总体坐标列向量,惯性坐标系下的总体坐标列阵$e$与浮动坐标系上总体坐标列阵$\tilde{e}$的关系如下
$e=A\tilde{e}$ (19)
式中：$A$是单元坐标变换矩阵,可以表示为
$A=\left[ \begin{matrix} {{A}_{0}} & 0 & \cdots & 0 \\ 0 & {{A}_{0}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & {{A}_{0}} \\ \end{matrix} \right]$ (20)
式中：$A$的维数等于节点坐标的总数;${{A}_{0}}$为一个$3\times 3$的正交矩阵;$\theta $为梁围绕固定轴的旋转角度,定义为
${{A}_{0}}=\left[ \begin{matrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$ (21)
将式（19）代入式（16）中,将其转化为浮动坐标系下旋转梁的动力学方程：
$\begin{matrix} MA\ddot{\tilde{e}}+2\dot{\theta }M{{A}_{\theta }}\dot{\tilde{e}}+\left( \ddot{\theta }M{{A}_{\theta }}-{{{\dot{\theta }}}^{2}}MA \right)\tilde{e}+ \\ K(\tilde{e})A\tilde{e}={{Q}_{\text{e}}} \\ \end{matrix}$ (22)
式中：$\dot{\theta }$、$\ddot{\theta }$分别为旋转角速度和旋转角加速度;${{A}_{\theta }}$为坐标变换矩阵$A$对旋转角度$\theta $的一次导数。
将式（22）等号两边同时左乘${{A}^{T}}$,MAQUEDA等[17]指出,在绝对节点坐标变换下,质量矩阵在正交坐标变换中的形式没有变化,即${{A}^{T}}MA=M$,同理,梁的刚度矩阵也具有同样的性质,可简化得到
$M\ddot{\tilde{e}}+2\dot{\theta }{{M}_{\text{TC}}}\dot{\tilde{e}}+\ddot{\theta }{{M}_{\text{TC}}}\tilde{e}-{{\dot{\theta }}^{2}}M\tilde{e}+K(\tilde{e})\tilde{e}={{A}^{T}}{{Q}_{\text{e}}}$ (23)
式中：${{M}_{\text{TC}}}={{A}^{T}}M{{A}_{\theta }}$。
2.4 动力学方程线性化
采用摄动理论对旋转动力学方程式（23）分别进行$\ddot{\tilde{e}}$、$\dot{\tilde{e}}$和$\tilde{e}$的线性化。当梁在没有外力情况下以稳定的角速度旋转时,得到的旋转梁振动方程为
$M\delta \ddot{\tilde{e}}+2\dot{\theta }{{M}_{\text{TC}}}\delta \dot{\tilde{e}}+\left[ {{K}_{\text{TC}}}\left( {{{\tilde{e}}}_{\text{ep}}} \right)-{{\theta }^{2}}M \right]\delta \tilde{e}=0$ (24)
式中：${{\tilde{e}}_{\text{ep}}}$为当前时刻旋转梁的平衡位置,${{K}_{\text{TC}}}({{\tilde{e}}_{\text{ep}}})$为刚度矩阵的偏导数与其自身的和,表示为
${{K}_{\text{TC}}}({{\tilde{e}}_{\text{ep}}})=\frac{\partial \left[ K({{{\tilde{e}}}_{\text{ep}}}) \right]}{\partial {{{\tilde{e}}}_{\text{ep}}}}{{\tilde{e}}_{\text{ep}}}+K({{\tilde{e}}_{\text{ep}}})$ (25)
当梁处于平衡位置时,有$\dot{\tilde{e}}=\text{0}$、$\ddot{\tilde{e}}=\text{0}$,代入式（23）,得到非线性方程,通过Newton-Raphson迭代法对该方程求解,以此确定梁处于静力平衡时的位置坐标${{\tilde{e}}_{\text{ep}}}$。
$-{{\dot{\theta }}^{2}}M{{\tilde{e}}_{\text{ep}}}+K({{\tilde{e}}_{\text{ep}}}){{\tilde{e}}_{\text{ep}}}=\text{0}$ (26)
利用得到的平衡位置坐标${{\tilde{e}}_{\text{ep}}}$,令
$z=\left[ \begin{matrix} \delta \tilde{e} \\ \delta \dot{\tilde{e}} \\ \end{matrix} \right]$ (27)
可将式（24）改为矩阵表达式,如下式所示：
$\left[ \begin{matrix} {{K}_{\text{TC}}}({{{\tilde{e}}}_{\text{ep}}}) & 0 \\ 0 & M \\ \end{matrix} \right]\dot{z}+\left[ \begin{matrix} 0 & -{{K}_{\text{TC}}}({{{\tilde{e}}}_{\text{ep}}}) \\ {{K}_{\text{TC}}}({{{\tilde{e}}}_{\text{ep}}}) & 2\dot{\theta }{{M}_{\text{TC}}} \\ \end{matrix} \right]z=0$ (28)
求解得到状态方程：
$\left[ {{K}_{\text{TC}}}({{{\tilde{e}}}_{\text{ep}}})-{{{\dot{\theta }}}^{2}}M \right]-{{\omega }^{2}}M=0$ (29)
通过求解状态方程可以获得固有频率$\omega $及其各阶振型。
3 仿真算例
根据上述绝对节点坐标法构建的动力学模型,编写对应的MATLAB程序,通过两个算例验证本模型的准确性,以此来分析风力机旋转复合材料叶片的动力学特性。
3.1 算例一：定转速旋转梁
由于风力机叶片旋转与旋转梁的运动较为相似,梁的一端固定,绕着定轴按照设定角度旋转,所以选用该算例来验证模型准确性。在该算例中,使用文献[18]相同参数,梁绕轴旋转的转动角度随时间变化的函数如下：
$\theta =\left\{ \begin{matrix} \frac{{{\omega }_{s}}}{{{T}_{s}}}\left\{ \frac{1}{2}{{t}^{2}}+{{\left( \frac{{{T}_{s}}}{2\text{ }\!\!\pi\!\!\text{ }} \right)}^{2}}\left[ \cos \left( \frac{2\text{ }\!\!\pi\!\!\text{ }t}{{{T}_{s}}} \right)-1 \right] \right\} & t\le {{T}_{s}} \\ {{\omega }_{s}}\left( t-\frac{{{T}_{s}}}{2} \right) & t\ge {{T}_{s}} \\ \end{matrix} \right.$ (30)
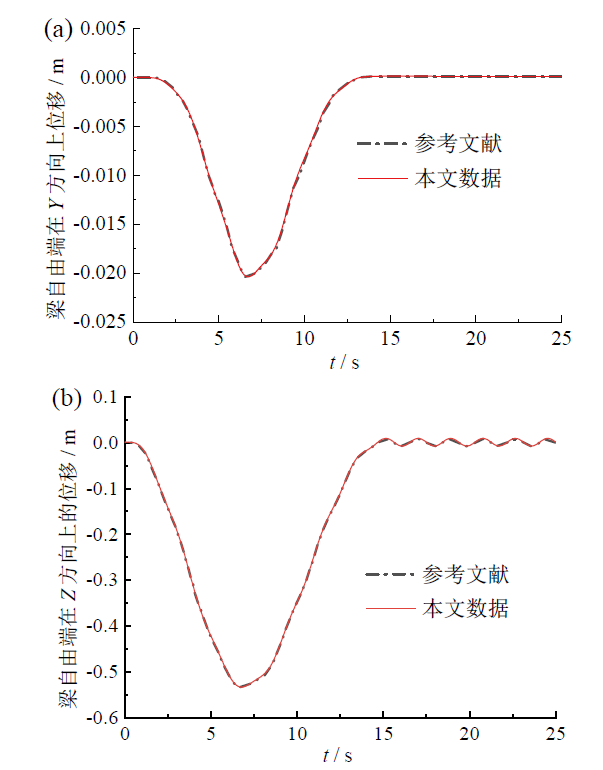
Fig. 3 Y-direction displacement (a) and Z-direction displacement (b) of the beam free end at different time points图3 不同时刻梁自由端Y方向位移（a）和Z方向位移（b） |
3.2 算例二：复合材料梁的固有频率
Table 4 The natural frequencies of a composite beam表4 复合材料的固有频率 |
| 阶次 | 固有频率 / Hz | 误差 / % | |
|---|---|---|---|
| 本文 | 文献[19] | ||
| 一阶 | 2.962 | 3.00 | 1.28 |
| 二阶 | 5.266 | 5.19 | -1.44 |
| 三阶 | 18.327 | 19.04 | 3.89 |
| 四阶 | 33.241 | 32.88 | -1.09 |
| 五阶 | 52.573 | 54.69 | 4.03 |
| 六阶 | 89.257 | 93.39 | 4.63 |
4 风力机叶片动力特性分析
为模拟叶片绕着轮毂旋转的工况,将叶片旋转中心设置在离叶根处Rhub = 2.8 m的位置,此时惯性坐标系下的总体坐标列阵$e$与浮动坐标系上总体坐标列阵$\tilde{e}$的关系为$e=A\tilde{e}-{{R}_{hub}}AH$,同时结合上节旋转梁的动力学方程,化简为
$M\ddot{\tilde{e}}+2\dot{\theta }{{M}_{\text{TC}}}\dot{\tilde{e}}+\ddot{\theta }{{M}_{\text{TC}}}\tilde{e}-{{\dot{\theta }}^{2}}M\tilde{e}-{{R}_{hub}}{{\dot{\theta }}^{2}}MH+K(\tilde{e})\tilde{e}=\text{0}$(31)
式中：$H={{\left[ \begin{matrix} 1 & 0 & \ldots & 0 & 1 & 0 & \ldots & 1 \\ \end{matrix} \right]}_{1\times 24}}$。
线性化方程（31）,获得其状态方程,并求解出叶片静止时以及不同转速下的固有频率和振型。
4.1 叶片静止时的模态
Table 5 Modal analysis results of static blade表5 静止叶片的模态分析结果 |
| 阶次 | 振型 | 固有频率 / Hz | 误差 / % | |
|---|---|---|---|---|
| 本文 | 文献[13] | |||
| 一阶 | 一阶挥舞 | 0.599 | 0.61 | -1.82 |
| 二阶 | 一阶摆振 | 0.948 | 0.93 | 1.96 |
| 三阶 | 二阶挥舞 | 1.748 | 1.74 | 0.47 |
| 四阶 | 二阶摆振 | 2.892 | 2.76 | 4.77 |
| 五阶 | 三阶挥舞 | 3.682 | 3.57 | 3.13 |
| 六阶 | 三阶摆振 | 5.902 | 5.69 | 3.72 |
| 七阶 | 一阶扭转 | 6.100 | 6.11 | -0.16 |
| 八阶 | 四阶挥舞 | 6.401 | 6.66 | -3.89 |
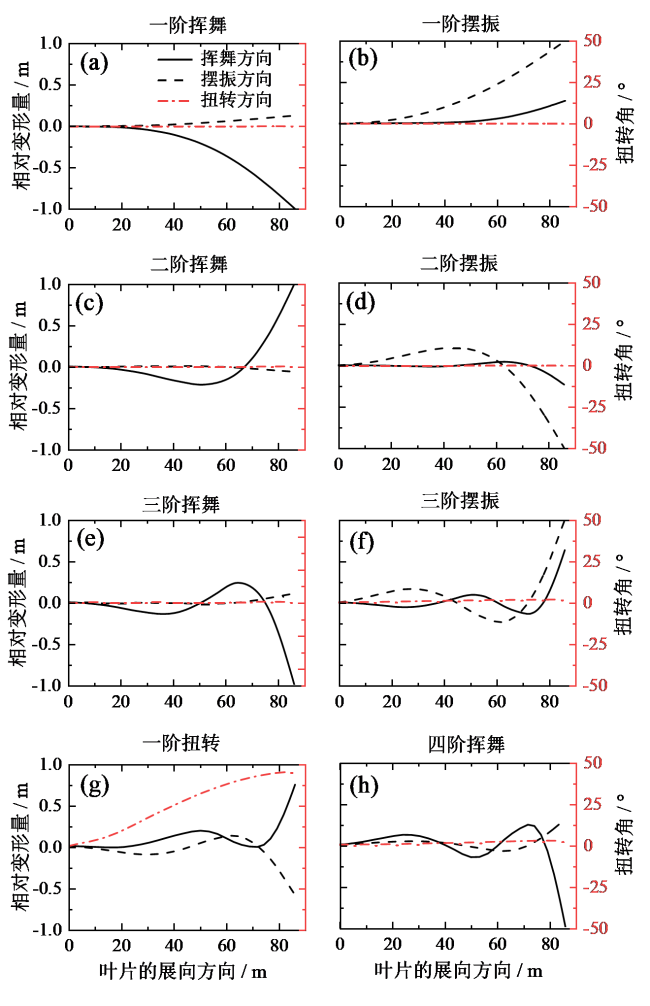
Fig. 4 The first eight vibration modes of static blade图4 静止时叶片的前八阶振型 |
由图4可见,叶片振型随着阶数的增大而存在显著耦合。低阶振型主要为挥舞和摆振,高阶时叶片在第六阶开始出现扭转,第七阶为挥舞、摆振、扭转三者之间的耦合运动。
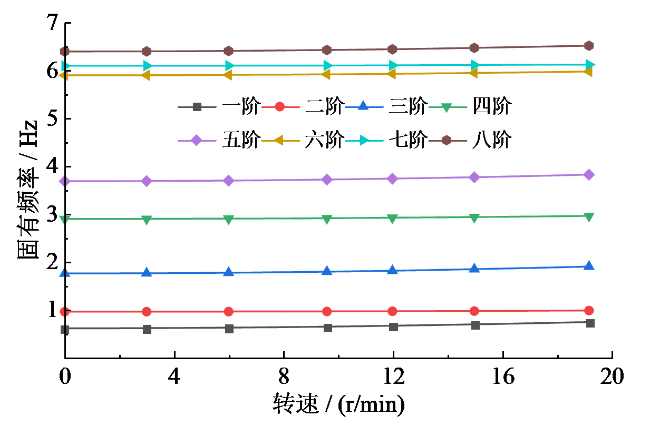
4.2 不同转速下叶片的固有频率
为研究叶片柔性变形与大范围刚性转动对叶片固有频率的影响,进一步通过绝对节点坐标法分别对3.0、6.0、9.6（额定转速）、12.0、15.0、19.2 r/min时进行模态特性分析,前八阶固有频率随转速的变化趋势如图5所示。
Fig. 5 Natural frequencies of blades at different rotational speeds图5 叶片在不同转速下的固有频率 |
由图5可以看出,叶片旋转时,由于动力刚化效应,叶片的各阶频率会随着转速的提高而改变,并对振型的挥舞和摆振产生较大影响。其中当转速达19.2 r/min时,相对于静止时的频率,一阶、二阶挥舞频率分别增加了0.131 Hz和0.145 Hz,增加幅度为21.96%和8.32%;摆振方向分别增加了0.024 Hz和0.063 Hz,增加幅度为2.57%和2.18%。
5 结论
采用绝对节点坐标法,基于一般连续介质力学理论和复合材料本构关系,建立柔性梁的非线性动力学模型,并通过不同算例验证该模型动态特性的正确性。为了描述叶片的转动,结合浮点坐标法,建立风力机旋转复合材料叶片的非线性动力学模型,并使用线性化方法得到其状态方程,将该模型应用于10 MW风力机叶片的动态特性分析,计算了该叶片在不同转速下的固有频率和振型。通过绝对节点坐标法对风力机旋转复合材料叶片的建模及其动态特性进行分析,结论如下：
（1）通过两个算例验证了所建立的绝对节点坐标法模型能够分析几何非线性变形问题,并应用到叶片的模态分析中,所得结果与参考文献结果一致。
（2）在绝对节点坐标法基础上结合高斯积分与Hammer积分,通过对叶片截面信息处理可进行复杂积分的运算,实现复杂截面叶片模型动力学方程的建立。
（3）在静止时,叶片振型随着阶数的增大而出现耦合现象。低阶振型主要为挥舞振动和摆振振动,叶片在第六阶开始出现扭转,第七阶为挥舞、摆振、扭转三者之间的耦合运动。
（4）在不同转速下,由于动力刚化效应,在挥舞方向比摆振方向更容易受叶片转速的影响。