0 引言
弯扭耦合对风力机叶片气动弹性响应有重要影响。叶片在气动力作用下弯曲后,会改变攻角的大小,进而改变叶片的气动力,形成反馈循环。弯扭耦合可以由叶片的几何形状（几何耦合）或各向异性叶片材料（材料耦合）引起。几何耦合是叶片几何形状弯曲的结果（预弯曲、后掠或负载偏移）,从而引起额外的扭转。材料耦合是叶片表皮或梁帽的纤维方向偏离主方向,从而引起弯曲和扭转的耦合。
随着风力机叶片长度和柔性的增加,叶片的非线性效应越加显著。KALLESØE[5]采用非线性二阶 Bernoulli-Euler梁理论,研究了5 MW叶片弯曲变形对气弹稳定性的影响,表明叶片的几何非线性对其气弹稳定性有明显的影响。传统采用欧拉梁结构模型[6]或模态法[7]构建叶片结构模型,难以表达柔性叶片的几何非线性变形。由于风力机叶片气弹耦合状态方程的建立比较复杂,基于频域的颤振分析研究相对较少,黄俊东等[8]采用多体动力学方法和叶素动量理论的方法建立叶片气弹耦合方程,研究了美国可再生能源实验室（National Renewable Energy Laboratory, NREL）发布的5 MW风力机气弹稳定性问题。和其他非线性模型相比,几何精确梁模型可以更为准确方便地计算叶片的变形位置以及叶片扭转的角度。通过在截面刚度矩阵中加入耦合项,研究由叶片材料引起的弯扭耦合问题。在结构动力学求解时,对结构动力学方程进行线性化处理,可以方便地与气动力线性化结合起来,进行特征值分析。
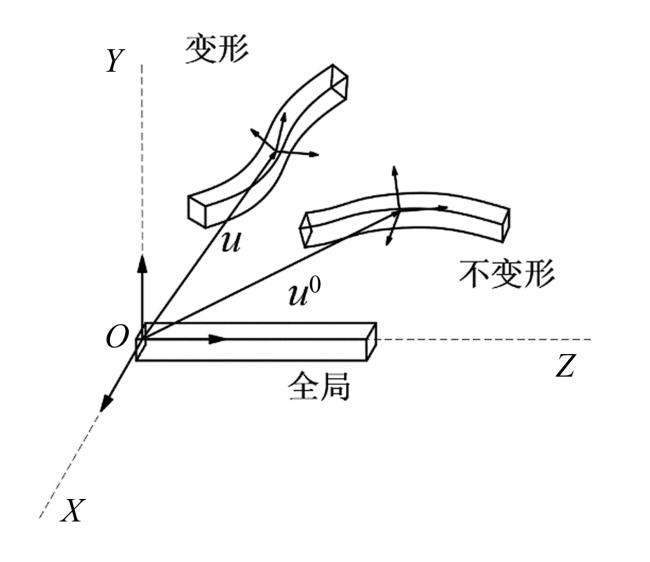
1 几何精确梁变形的描述
几何精确梁采用平截面假设,梁的位形由梁轴线的位移和相应截面的转动决定。如图1有全局坐标系（不考虑叶片预弯预扭以及截面偏心等因素）、不变形位置坐标系（考虑叶片真实几何形状）和变形位置坐标系（考虑气弹耦合后叶片的变形）。
Fig. 1 The rotating coordinate system of the beam图1 梁的转动坐标系 |
在变形位置,梁上任意一点p的位置向量可以写为
${{u}_{p}}\left( t,z,x,y \right)=u\left( t,z \right)+\Lambda {{\bar{R}}_{p}}\left( x,y \right)$ (1)
式中：${{u}_{p}}$为剪切中心在全局坐标系下的坐标;z为截面在梁轴线上的坐标;$\Lambda $为截面转动矩阵;${{\overline{R}}_{p}}$为截面坐标系下的位置向量。叶片坐标系的建立为,在叶片根部以各个截面的剪心为原点,建立局部坐标系,将局部坐标系平移和旋转后,得到叶片的真实几何形状。
三维旋转矩阵$\Lambda $有9个元素,包含6个约束关系,难以直接作为姿态变量,欧拉四元数是描述截面转动非奇异的最小参数表达,本文采用欧拉四元数$\hat{q}$描述截面的转动[11]。
$\hat{q}=\left( {{q}_{0}},q \right)={{\left( {{q}_{0}},{{q}_{1}},{{q}_{2}},{{q}_{3}} \right)}^{T}}$ (2)
式中：四元数之间满足$q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}=1$;${{}^{T}}$表示向量的转置。
四元数$\hat{q}$和转动矩阵$\Lambda $的关系为
$\Lambda =\left( 2q_{0}^{2}-1 \right)I+2{{q}_{0}}\hat{q}+2q{{q}^{T}}$ (3)
2 结构动力学方程的建立
2.1 几何精确梁本构关系
$\left(\begin{array}{l}N \\ M \end{array}\right)=S\left(\begin{array}{l} \Gamma \\ K\end{array}\right)$ (4)
式中：S为6 × 6截面刚度矩阵。不考虑耦合时,S矩阵只包含对角线元素。通过在截面刚度矩阵S中设置耦合项${{K}_{46}}$可以引入挥舞扭转耦合。
${{K}_{46}}=\gamma \sqrt{{{K}_{44}}{{K}_{66}}}$ (5)
式中：$\gamma $为挥舞扭转耦合系数[9];${{K}_{44}}$和${{K}_{66}}$分别为挥舞刚度和扭转刚度。
应变与变形的关系为
$\Gamma ={{\Lambda }^{T}}{u}'-{{\Gamma }_{0}}$ (6)
$\hat{K}={{\left( 0,{{K}_{1}},{{K}_{2}},{{K}_{3}} \right)}^{T}}=2{{\hat{q}}^{*}}\circ {\hat{q}}'-{{\hat{K}}_{0}}$ (7)
式中：${{\Gamma }_{0}}$和${{\hat{K}}_{0}}$为梁的初始位置和曲率参数;${{( )}^{\prime }}$为在参考构形中对截面在z轴上坐标的导数;$\circ $为四元数乘法。
2.2 动力学平衡方程
首先建立风力机叶片弱形式动力学平衡方程[14],然后通过数值积分和微分方法离散求解。
对内力沿单元轴线积分,得到内力虚功为[15]
$\delta W_{\operatorname{int}}^{e}=\int\limits_{0}^{{{l}_{e}}}{\left( \delta {{\Gamma }^{T}}N+\delta {{K}^{T}}M \right)}\text{d}Z$ (8)
对气动力沿轴线积分,重力进行体积积分,得到单元的外力虚功
$\delta W_{ext}^{e}=\int\limits_{0}^{{{l}_{e}}}{\left( \delta u_{\text{a}}^{\text{T}}{{f}_{\text{a}}}+\delta \theta _{\text{a}}^{\text{T}}{{m}_{\text{a}}} \right)}\text{d}Z+\int\limits_{V}{\delta u_{\text{p}}^{T}\rho g\text{d}V}$ (9)
式中：$\delta {{u}_{\text{a}}}$为轴线气动节点的虚位移;$\delta {{\theta }_{a}}$为轴线节点气动点的虚转动;${{f}_{a}}$为轴线节点的气动力向量;${{m}_{a}}$为轴线节点的气动弯矩向量;g为重力加速度向量;$\rho $为叶片体密度;${{l}_{\text{e}}}$为单元长度;下标e表示叶片单元。
各点的速度进行体积分,得到单元的惯性力虚功
$\delta W_{inert}^{e}=\int\limits_{V}{\delta u_{p}^{T}}\rho {{\ddot{u}}_{p}}\text{d}V$ (10)
根据虚功原理,单元内力、外力和惯性力虚功满足
$\delta W_{\operatorname{int}}^{e}-\delta W_{ext}^{e}+\delta W_{inert}^{e}=0$ (11)
$\begin{align}& \delta W_{\operatorname{int}}^{e}=\delta {{d}^{eT}}{{R}_{\operatorname{int}}} \\ & \delta W_{\text{ext}}^{e}=\delta {{d}^{eT}}{{R}_{\text{ext}}} \\ & \delta W_{\text{inert}}^{e}=\delta {{d}^{eT}}{{R}_{\text{inert}}} \\ \end{align}$ (12)
单元节点k虚位移表示为
$\delta {{d}_{k}}=\left[ \delta {{x}_{k}}\text{ }\delta {{y}_{k}}\text{ }\delta {{z}_{k}}\text{ }\delta {{\theta }_{x}}_{k}\text{ }\delta {{\theta }_{y}}_{k}\text{ }\delta {{\theta }_{z}}_{k} \right]$ (13)
单元位移$\delta {{d}^{e}}=[\delta {{d}_{1}}\text{ }\delta {{d}_{2}}\text{ }\cdot \cdot \cdot \text{ }\delta {{d}_{K}}]$。
把式（12）代入式（11）,并在全局坐标系下进行组装,得到等效节点内力、外力和惯性力的离散平衡方程
${{R}_{int}}-{{R}_{ext}}+{{R}_{inert}}=0$ (14)
3 动力学方程线性化
为了构建叶片气弹线性平衡方程,形成特征值求解,需要对动力学平衡方程进行线性化处理。分为两个部分,第一部分是结构动力学方程线性化,第二部分是气动力线性化。
3.1 结构动力学线性化
分别对节点内力、外力和惯性力矩阵线性化[15]得到
$\delta {{R}_{\operatorname{int}}}={{K}_{\operatorname{int}}}\delta d$ (15)
$\delta {{R}_{ext}}={{K}_{ext}}\delta d+\sum{\mu \omega {{B}^{T}}\left( \delta {{F}^{a}} \right)B\delta d}$ (16)
$\delta {{R}_{inert}}={{K}_{inert}}\delta d+{{C}_{inert}}\delta \dot{d}+{{M}_{inert}}\delta \ddot{d}$ (17)
将式（15） ~ 式（17）代入平衡方程（14）可以得到
$M\delta \ddot{d}+C\delta \dot{d}+K\delta d-\sum{\mu \omega {{B}^{T}}\left( \delta {{F}^{a}} \right)}B\delta d=0$ (18)
式中：$K={{K}_{\operatorname{int}}}-{{K}_{ext}}+{{K}_{inert}}$;$M={{M}_{inert}}$;$C={{C}_{inert}}$;$\mu $为弱形式求积长度系数[16];$\omega $为Gauss-Lobatto积分系数;B为微分求积定位矩阵。
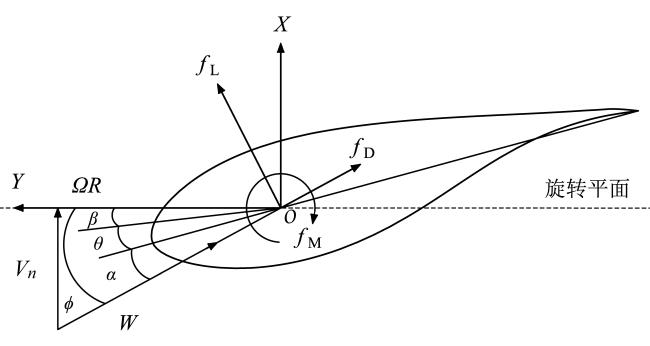
3.2 气动力线性化
根据叶素动量定理,作用在叶片第k个截面的气动力可以写为
$f_{k}^{a}=\frac{1}{2}{{\rho }_{a}}{{c}_{k}}W_{k}^{2}C_{k}^{{}}$ (19)
式中：c为截面弦长;${{\rho }_{a}}$为空气密度;$W$为相对来流风速;$C={{\left( {{C}_{\text{L}}},{{C}_{\text{D}}},{{C}_{\text{M}}} \right)}^{\text{T}}}$,其中${{C}_{\text{L}}}$、${{C}_{\text{D}}}$、${{C}_{\text{M}}}$分别为升力系数、阻力系数和扭矩系数。
考虑叶片振动和入流角的影响,相对来流风速$W$和攻角α可以写为
$W=\sqrt{{{\left( Vn-\dot{x} \right)}^{2}}+{{\left( \text{ }\!\!\Omega\!\!\text{ }R+\dot{y} \right)}^{2}}}$ (20)
$\alpha =\phi -\theta -\beta =t{{g}^{-1}}\left( \frac{Vn-\dot{x}}{\text{ }\!\!\Omega\!\!\text{ }R+\dot{y}} \right)-\theta -\beta $ (21)
式中：Vn为垂直旋转平面的来流风速;ϕ为入流角;β为桨距角;θ为叶片扭角;$\dot{y}$和$\dot{x}$分别为摆振和挥舞方向振动速度;R为翼型截面剪心到轮毂中心的距离;$\Omega $为叶片旋转速度,见图2。
Fig. 2 Blade airfoil section图2 叶片翼型截面 |
当来流风速和叶片旋转速度均已确定时,叶片在某一瞬时受到的气动力是振动速度的函数。为研究在某一工况下气动力对叶片振动特性的影响,首先将$f_{{}}^{a}$进行坐标转换,得到全局坐标下的气动力$F_{{}}^{a}$,然后采用变分原理对气动力进行线性化处理。在线性化的过程中,为了考虑涡旋脱落和尾缘流动分离对气动特性的影响,引入基于状态变量${{x}^{\text{a}}}={{\left\{ {{x}_{1}}\text{ }{{x}_{2}}\text{ }{{x}_{3}}\text{ }{{x}_{4}} \right\}}^{T}}$的B-L动态失速模型[17],修正叶片各翼型截面处的升力系数及其斜率。
气动载荷的线性化表示为[8]
$\delta {{F}^{a}}={{M}_{a}}\delta \ddot{d}+{{C}_{a}}\delta \dot{d}+{{K}_{a}}\delta d+{{K}_{f}}\delta {{x}^{a}}$ (22)
式中：${{K}_{a}}$、${{M}_{a}}$、${{C}_{a}}$分别是气动部分线性化得到的气动质量阵、刚度阵和阻尼阵;${{\mathbf{K}}_{f}}$为状态变量系数矩阵。
对状态变量线性化[6]得到
$\delta {{\dot{x}}^{a}}+{{A}_{d}}\delta {{x}^{a}}={{M}_{s}}\delta \ddot{d}+{{C}_{s}}\delta \dot{d}+{{K}_{s}}\delta d$ (23)
式中：${{M}_{s}}$、${{K}_{s}}$、${{C}_{s}}$分别为状态变量线性化引入的质量阵、刚度阵和阻尼阵;${{A}_{d}}$为系数矩阵。
联立式（18）、式（22）和式（23）,气弹线性平衡方程可以写为
$\left\{ \begin{align} & \left( M-{{M}_{a}} \right)\delta \ddot{d}+\left( C-{{C}_{a}} \right)\delta \dot{d}+ \\ & \left( K-{{K}_{a}} \right)\delta d-{{K}_{f}}\delta {{x}^{a}}=0 \\ & {{{\dot{x}}}^{a}}+{{A}_{d}}{{x}^{a}}={{M}_{s}}\delta \ddot{d}+{{C}_{s}}\delta \dot{d}+{{K}_{s}}\delta d \\ \end{align} \right.$ (24)
4 特征值复模态计算
根据式（24）建立风力机颤振分析的特征值平衡方程
$\left( \bar{K}+\lambda \bar{M} \right)y=\text{0}$ (25)
设$y={{(\delta d,\delta \dot{d},{{x}^{a}})}^{T}}$,其解的形式为$y=Y{{\text{e}}^{\lambda t}}$;其中
$\overline{\boldsymbol{K}}=\left[\begin{array}{ccc}0 & -\boldsymbol{I} & 0 \\\boldsymbol{K}-\boldsymbol{K}_{\mathrm{a}} & \boldsymbol{C}-\boldsymbol{C}_{\mathrm{a}} & -\boldsymbol{K}_{\mathrm{f}} \\-\boldsymbol{K}_{\mathrm{s}} & -\boldsymbol{C}_{\mathrm{s}} & \boldsymbol{A}_{\mathrm{d}}\end{array}\right]$ (26)
$\overline{\boldsymbol{M}}=\left[\begin{array}{ccc}\boldsymbol{I} & 0 & 0 \\0 & \boldsymbol{M}-\boldsymbol{M}_{\mathrm{a}} & 0 \\0 & -\boldsymbol{M}_{\mathrm{s}} & \boldsymbol{I}\end{array}\right]$ (27)
利用Matlab软件提供的eig函数计算特征值和特征向量,得到叶片的气弹频率、气弹阻尼比和振型,其中特征值的虚部为气弹频率,特征值的实部为气弹阻尼比。
${{\bar{f}}_{i}}=\frac{\text{Im}\left( {{\lambda }_{i}} \right)}{2\text{ }\!\!\pi\!\!\text{ }},{{\bar{\delta }}_{i}}=-\frac{\text{Re}\left( {{\lambda }_{i}} \right)}{2\text{ }\!\!\pi\!\!\text{ }{{{\bar{f}}}_{i}}}$ (28)
式中：Im为复特征值的虚部;Re为复特征值的实部。
5 计算结果
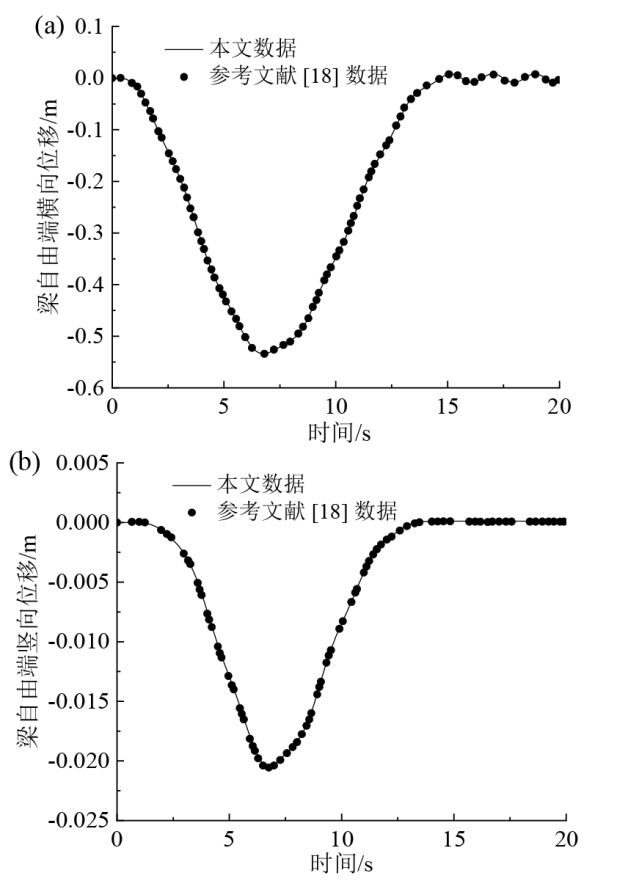
5.1 旋转梁算例
旋转梁作为能否处理梁大变形标准算例,受到广泛的关注。通过与参考文献[18]对比来验证动力学方程的正确性,梁的旋转角度随时间变化的函数为
$\varphi (t)=\left\{ \begin{align} & \frac{{{\omega }_{s}}}{{{T}_{s}}}\left[ \frac{{{t}^{2}}}{2}+{{\left( \frac{{{T}_{s}}}{2\text{ }\!\!\pi\!\!\text{ }} \right)}^{2}}\left( \cos \frac{2\text{ }\!\!\pi\!\!\text{ }t}{{{T}_{s}}}-1 \right) \right]\text{ }0\le t\le {{T}_{\text{s}}} \\ & {{\omega }_{s}}\left( t-\frac{{{T}_{s}}}{2} \right)\text{ }t>{{T}_{\text{s}}} \\ \end{align} \right.$(29)
式中：Ts = 15 s;${{\omega }_{s}}=$4 rad/s。
Fig. 3 Longitudinal (a) and transverse (b) deflections at the tip of the rotating beam图3 梁自由端横向偏转（a）和竖向偏转（b） |
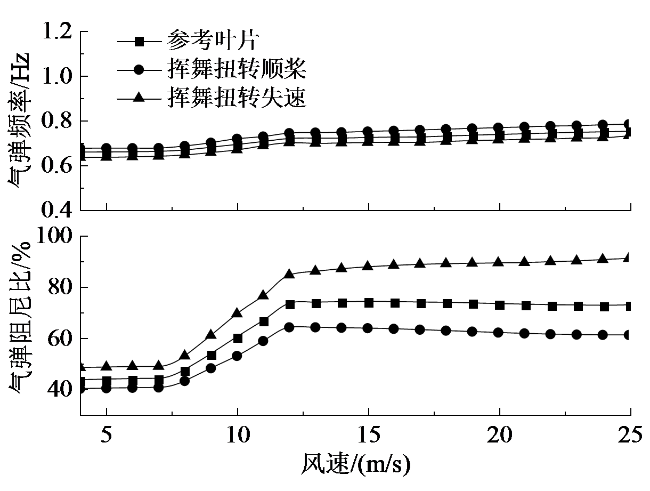
5.2 运行工况下气弹阻尼和气弹频率
由于材料的各向异性,风力机叶片截面耦合特性比较复杂,为了单独研究挥舞扭转耦合对叶片颤振特性的影响,将丹麦技术大学[10]提供的10 MW风力机叶片（截面刚度不包含耦合项）设为参考叶片。在叶片中间部分某截面的刚度参数如式（30）。
${{K}_{cs}}=\left[ \begin{matrix} 0.514 & 0 & 0 & 0 & 0 & 0 \\ {} & 0.378 & 0 & 0 & 0 & 0 \\ {} & {} & 7.57 & 0 & 0 & 0 \\ {} & {} & {} & 3.38 & 0 & 0 \\ {} & sym. & {} & {} & 11.5 & 0 \\ {} & {} & {} & {} & {} & 0.661 \\ \end{matrix} \right]\times {{10}^{9}}$ (30)
截面耦合系数$\gamma =-0.1$为挥舞顺桨耦合叶片,挥舞顺桨耦合会减小攻角。截面耦合系数$\gamma =0.1$为挥舞失速耦合叶片,挥舞失速耦合会增大攻角。在运行工况下考察挥舞扭转耦合对叶片气弹模态特性的影响。
图4显示了运行工况下,挥舞扭转耦合对一阶挥舞模态气弹频率和气弹阻尼的影响。在风力机运行工况下,三种叶片的一阶挥舞气弹频率和气弹阻尼比的变化趋势基本相同。具体为在风速4 ~ 7 m/s,一阶挥舞气弹阻尼比保持不变,在风速7 ~ 12 m/s,为上升趋势,风速12 m/s后保持平稳,此时风力机达到额定转速运行工况下,一阶挥舞气弹频率变化趋势与气弹阻尼比相似。相比于参考叶片,挥舞顺桨耦合增大了一阶挥舞气弹频率,降低了一阶挥舞气弹阻尼比,挥舞失速耦合降低了一阶挥舞气弹频率,增大了一阶挥舞气弹阻尼比。
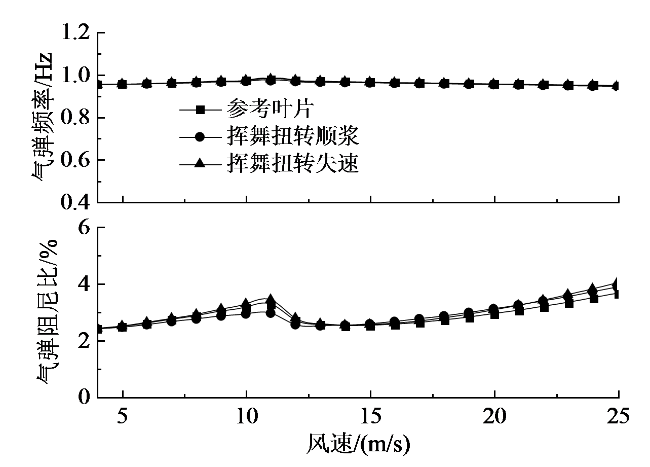
Fig. 4 First flapwise aeroelastic frequency and damping under the operational wind speed图4 运行工况下一阶挥舞气弹频率和气弹阻尼比 |
挥舞扭转耦合对一阶摆振气弹频率和气弹阻尼的影响如图5所示。在运行工况下,三种叶片的一阶摆振气弹频率基本重合,一阶气弹阻尼也比较接近,表明挥舞扭转耦合对一阶摆振模态气弹特性影响较小。在运行工况下,三种叶片的一阶摆振气弹频率变化较小,变化区间为0.945 ~ 0.979 Hz。一阶摆振气弹阻尼比变化趋势为,在风速为4 ~ 11 m/s时缓慢上升,然后短暂下降后又继续保持上升,一直到风速25 m/s时达到最大值,此时气弹阻尼比大约为4%,与风速11 m/s时的气弹阻尼接近。
Fig. 5 First edgewise aeroelastic frequency and damping under the operational wind speed图5 运行工况下一阶摆振气弹频率和气弹阻尼比 |
5.3 定叶尖速比工况下颤振风速
为了研究弯扭耦合对风力机叶片颤振风速的影响,将风力机叶片运行工况设为定叶尖速比10,即风力机叶尖速度为来流风速的10倍,并将叶片的桨距角设为0。结果如图6。
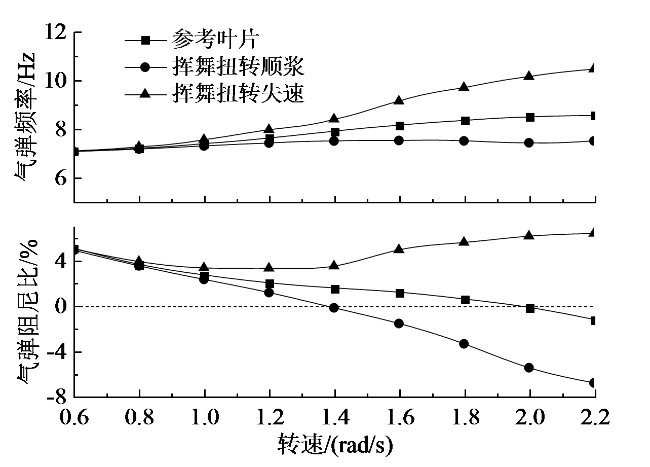
Fig. 6 First torsion aeroelastic frequency and aeroelastic damping under constant tip speed ratio图6 定叶尖速比工况下一阶扭转气弹频率和气弹阻尼比 |
挥舞顺桨耦合叶片一阶扭转气弹阻尼比在转速1.38 rad/s时出现负值,此时一阶扭转气弹频率为7.51 Hz,参考叶片大约在转速1.97 rad/s时出现负值,此时一阶扭转气弹频率为8.47 Hz,挥舞扭转失速耦合叶片没有出现负值。表明挥舞顺桨耦合会降低风力机叶片的颤振风速。这种现象的原因可能是,挥舞顺桨耦合叶片变形小,造成扭转刚度小于参考叶片,根据文献[19],扭转刚度降低会使叶片的颤振风速降低。
6 结论
采用非线性几何精确梁模型和叶素动量定理建立风力机叶片的气弹模型,在Beddoes-Leishman动态失速模型的基础上对气弹模型线性化,构建特征平衡方程,通过特征值分析,计算风力机叶片的气弹频率和气弹阻尼比。通过在截面刚度矩阵中引入耦合系数,研究风力机叶片挥舞扭转耦合对气弹模态特性的影响。主要结论如下：
（1）在运行工况下,挥舞扭转耦合主要影响挥舞模态,对摆振模态影响较小。挥舞顺桨耦合增大了一阶挥舞模态气弹频率,降低了一阶挥舞模态气弹阻尼比;挥舞失速耦合降低了一阶挥舞模态气弹频率,增大了一阶挥舞模态气弹阻尼比。
（2）在定叶尖速比工况下,挥舞顺桨耦合风力机叶片一阶扭转气弹频率在风速1.38 rad/s出现负值,参考叶片一阶扭转气弹频率在风速1.97 rad/s出现负值,挥舞失速耦合一阶扭转气弹频率没有出现负值。截面耦合系数$\gamma =-0.1$时,挥舞顺桨耦合会降低风力机叶片的颤振风速,约降低了29%。
本文建立的气弹模型还可以用于分析风力机叶片其他的气弹问题。