0 引言
近年来,国内外诸多学者通过实验和数值模拟方法研究风力机尾流演化规律。ZHAO等[8]通过实验研究了风力机尾流的风廓线及速度亏损值的变化趋势。刘惠文等[9]通过实验测量了剪切来流条件下的风力机尾流的湍流积分长度的演变规律,发现在大于4倍直径的远尾流场存在不稳定的尾流弯曲现象。韩玉霞等[10]通过时间分辨粒子图像测速法（time resolved-particle image velocity, TR-PIV）研究了直径为300 mm的风力机尾流的拟序结构特征规律,发现大涡的拟序结构具有周期性,湍流强度增加,拟序结构易耗散。王泽栋等[5]和杨瑞等[11]分别研究了串列布置风力机的尾流影响,均发现增大风力机的间距可提高下游风力机发电功率。王泽栋等还发现增大来流湍流度和调整上游风力机的偏航角也可提高下游风力机发电功率。
本文采用风洞实验,对风力机缩比模型的尾流特征进行测量,同时对比0°、15°、30° 三种偏航角下风力机尾流参数的差异性,分析尾流区不同位置的速度分布及测点间速度相关性。
1 实验部分
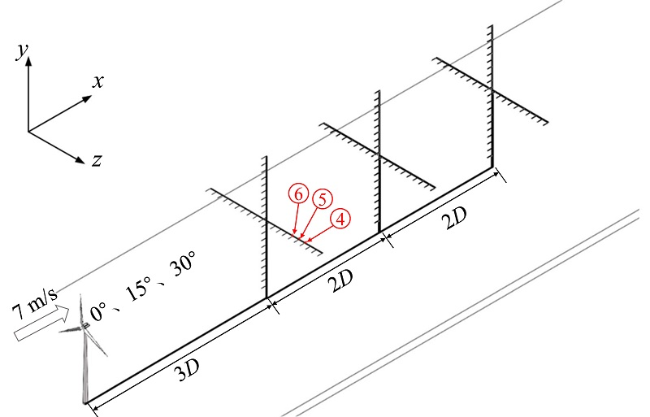
Fig. 1 Wind turbine and measuring point layout model图1 风力机及测点布置模型 |
结合实验所得的0°、15°、30° 不同偏航角下3D、5D、7D三个尾流轮毂高度位置的时序速度数据,通过分析风力机在不同偏航工况下的瞬时速度时序图,了解不同位置尾流的时序特征。此外,基于最大信息系数的特性,分析不同测点数据相关性。
2 结果与讨论
2.1 尾流时序特征
图2分别为风力机偏航角为0°、15°、30° 在不同尾流位置处的瞬时水平速度时序云图,并分别作平均速度曲线。偏航角为0° 时,如图2（a）所示,流向左右呈现对称现象,在3D位置处,位于轮毂中心（-0.25D,0.25D）位置处的风速明显减小,尾流速度亏损较大,尾流效应较为明显。但随着流向距离的增大,在5D、7D位置处的尾流速度逐渐恢复,使得尾流速度亏损减弱。从图2（b）可知,15° 偏航角下,3D位置（-0.1D,0.25D）范围内速度亏损较大。同时,图2（c）的30° 偏航角的3D位置（0,0.25D）范围内速度亏损较大,与图2（a）和图2（b）的尾流相似,在5D、7D位置处的尾流速度逐渐恢复,7D位置30° 偏航角尾流速度恢复最好,在15°和30° 偏航角时的最低速度位置在y/D = 0.1处。
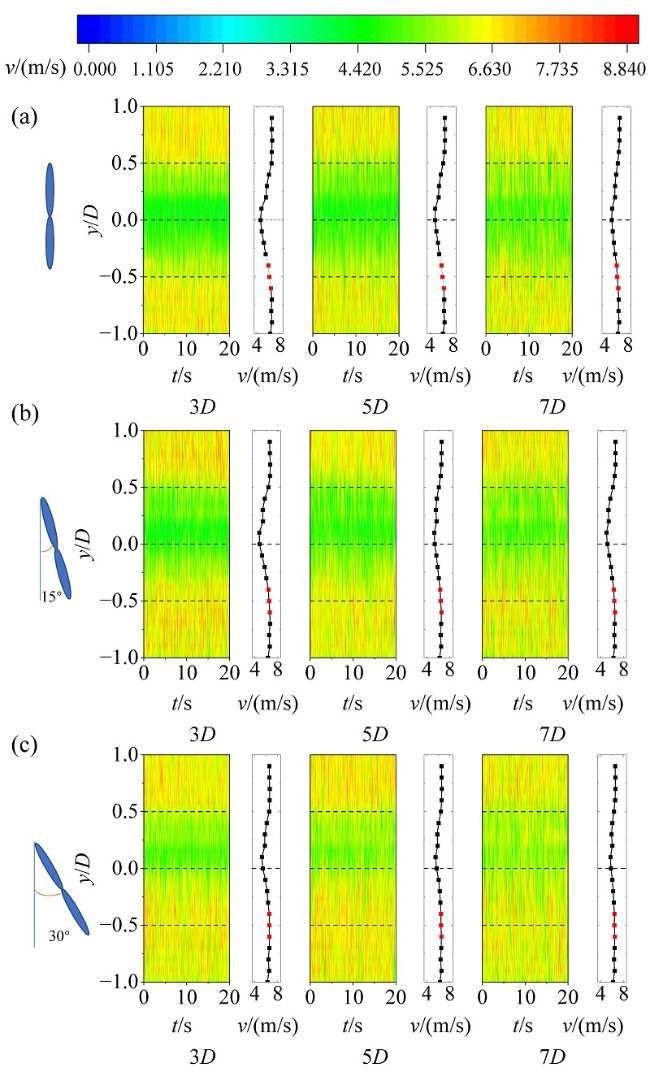
Fig. 2 Instantaneous speed sequence cloud chart and average velocity curve of wind turbine at 0° (a), 15° (b), and 30° (c) yaw angles图2 0°（a）、15°（b）、30°（c） 偏航角时风力机瞬时速度时序云图和平均速度曲线 |
2.2 最大信息化及相关性
MIC被用于检测变量之间的相关程度和机器学习的特征选择[20],该方法是将数据空间网格划分,不同网格中各点的分布情况可由各网格互信息表示：
$I\left( A;B \right)=\sum\limits_{a\in A}{{}}\sum\limits_{b\in B}{p(a,b)\log }\frac{p(a,b)}{p(a)p(b)} $ (1)
式中： $I\left( A;B \right) $为A、B的互信息; $p\left( a,b \right) $表示变量A、B的联合概率; $p(a) $、 $p(b) $分别表示变量A、B的边缘概率密度。
在不同划分标准的网格中最大的互信息值即为MIC值,表达为：
${{C}_{\text{MI}}}\left( A,B \right)={{\max }_{m\times n\le K}}\frac{I\left( A;B \right)}{{{\log }_{2}}\min \left( m,n \right)}$ (2)
式中：K表示划分网格的最大值;m、n分别为网格的行数和列数; ${{C}_{\text{MI}}}\left( A,B \right) $表示相关性系数,若该值大于0.95,则表示变量A和B显著相关[21]。
Table 1 Comparison of MIC values of measuring point ⑤ with different wake distances at different yaw angles表1 不同尾流距离的测点⑤的MIC值在不同偏航角的对比 |
| 偏航角 | MIC值 | ||
|---|---|---|---|
| 3D&5D | 3D&7D | 5D&7D | |
| 0° | 0.230 | 0.590 | 0.558 |
| 15° | 0.125 | 0.225 | 0.320 |
| 30° | 0.991 | 0.225 | 0.320 |
Table 2 MIC values between measuring points ④-⑥ under different yaw angles at 3D, 5D, and 7D positions表2 3D、5D、7D位置处不同偏航角时测点④ ~ ⑥之间的MIC值 |
| 位置点 | 偏航角 | MIC值 | |
|---|---|---|---|
| ④&⑤ | ⑤&⑥ | ||
| 3D | 0° | 0.991 | 0.991 |
| 15° | 0.558 | 0.991 | |
| 30° | 0.225 | 0.991 | |
| 5D | 0° | 0.991 | 0.991 |
| 15° | 0.590 | 0.590 | |
| 30° | 0.991 | 0.558 | |
| 7D | 0° | 0.991 | 0.590 |
| 15° | 0.590 | 0.558 | |
| 30° | 0.991 | 0.590 | |
根据统计学原理中相关系数理论[22],在偏航角为0° 时,3D与5D、3D与7D、5D与7D间同一测点位置处的MIC值分别为0.230、0.590、0.558,可知3D与5D处间的速度相关性并不明显,而3D与7D、5D与7D间的速度相关性呈强相关,风力机旋转的尾流周期效应导致近尾流与远尾流的MIC值有差距。当偏航角为15° 时,3D与5D、3D与7D、5D与7D间测点⑤处的MIC值分别为0.125、0.225、0.320,可知3D、5D、7D位置间速度相关性较小,表明3D、5D、7D位置相互间的速度影响较小。在30° 偏航工况条件下,3D与5D、3D与7D、5D与7D间同一测点位置处的MIC值分别为0.991、0.225、0.32。3D与5D间的速度相关性呈强相关,3D位置对5D位置的速度影响较大,在近尾流区域,尾流涡对测点⑤处的影响较小,导致其相关性较大。而3D与7D以及5D与7D间的速度影响较小。
由此可知,随着风力机偏航角度的增大,3D位置对5D位置速度影响先减小后增大,而3D对7D以及5D对7D的速度影响逐渐降低。
在0° 偏航工况下,3D、5D、7D位置处测点④与测点⑤的MIC值均为0.991,测点⑤与测点⑥间的MIC值分别为0.991、0.590、0.590。这说明在0° 偏航时,3D、5D、7D位置处在测点④与测点⑤位置间速度相互之间的影响很大,而在5D、7D位置处测点⑤与测点⑥间的影响虽然仍较大,但相比于3D位置仍有差距。当偏航工况为15° 时,3D、5D、7D位置处测点④与测点⑤的MIC值分别为0.558、0.590、0.590;测点⑤与测点⑥间的MIC值分别为0.991、0.590、0.558。3D、5D、7D位置处测点④和测点⑤间速度影响较大,且3D、5D、7D位置差异不大。而3D位置处测点⑤与测点⑥间速度影响相比于5D和7D位置最大,5D与7D位置处对测点⑤与测点⑥的速度影响较小,且5D与7D位置处差异不大。当偏航工况为30° 时,3D、5D、7D位置处测点④与测点⑤的MIC值分别为0.225、0.991、0.991,测点⑤与测点⑥间的MIC值分别为0.991、0.558、0.590。3D位置处测点④与测点⑤间的影响较小,5D、7D位置处测点④对测点⑤的影响很大;而3D位置处测点⑤与测点⑥间的速度影响很大,5D、7D位置处测点⑤与测点⑥的速度影响较小且差异不大。
因此,随着风力机偏航角的增大,3D位置处测点④与测点⑤的速度影响逐渐减小,而5D和7D位置处测点④与测点⑤间的速度影响先减小后增大;而3D位置处测点⑤对测点⑥的速度影响稳定不变且影响很大,5D和7D位置处上叶尖与测点⑥间的速度影响差异不大。
3 结论
通过分析风力机下游尾流时序云图研究了不同偏航工况下尾流的时序特征,利用最大信息化理论统计方法分析了特征点之间的相关性,得出以下结论：
风力机在不同偏航工况下,风力机水平方向上同一测点位置的速度相关性有明显区别,相比于0°与30° 偏航工况,风力机叶片偏航角为15° 时,水平方向上同一测点位置间的相关性最小,同一测点位置间速度的相互影响最小。且在风力机不同偏航工况下,风力机在3D、5D、7D位置处同一测点以及距离同一测点相等距离的两个测点相互间均存在影响,随着偏航角度的增大,尾流间相互影响先增大后减小,当风力机叶片偏航角为15° 时,尾流间的相互影响最小。
在风力机不同偏航工况下,随着风力机叶片偏航角和风力机水平方向距离的增大,尾流效应减弱,尾流宽度减小,尾流速度恢复程度越来越高。同时,偏航角的改变也导致了风力机尾流速度分布中平均速度最小值点的位置向轮毂方向偏移。