0 引言
风力发电是可再生能源中技术最成熟、发电小时数最高的发电技术。在“双碳”目标背景下,风能将作为替代化石能源的首要选择。我国风能资源丰富,陆上100 m高度风能的技术可开发量约为39亿千瓦[1]。国家政策大力支持风电发展,我国风电总装机规模达到了世界第一,陆上风电装机超过3亿千瓦[2],我国的风电开发还将继续快速发展。随着开发程度不断深入,陆上风电场可开发区域逐渐减小,陆上山地成为重点开发区域。陆上山地风电场地形起伏较大,交通不便,而风电机组重量大,运输困难,对道路要求高。此外,我国陆上风电已经全面进入“平价时代”,陆上风电电价不再享受补贴,在保证收益率的情况下,降低风电开发成本成为风电设计、建设过程追求的目标之一。
如图1所示,根据对湖南、云南和河南等地已建成山地风电场的调研和前人的研究结果[3,4],陆上山地风电场道路投资占总投资6% ~ 10%,占风电场建筑工程投资的30% ~ 60%。可见,在陆上山地风电场中,道路建设是风电场建设工程中的重要部分,道路的建设投资增大会严重影响风电场的经济指标,而优化风电场道路线路能够有效降低风电场投资、提高收益率。在项目可行性研究阶段,风电场道路路线主要是通过人工经验确定道路走线的中心线位置,使路径满足风电场运输对转弯半径、坡度的要求。设计过程中采用纬地、海地等道路设计专用软件进行辅助设计[5]。这种半经验方法依赖设计人员的工程经验,设计过程中劳动强度大,重复性工作多,导致设计效率低、设计结果达不到优化,从而难以保障项目经济性。因此,为了高效、准确获取经济性高的道路设计方案,亟需优化算法进行道路路线优化。
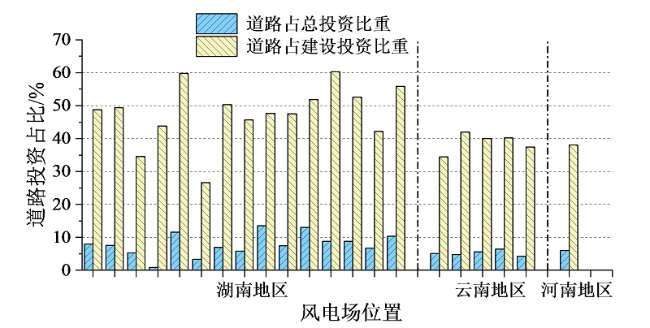
Fig. 1 Proportion of wind farm road investment图1 风电场道路投资占比 |
目前道路路线优化算法方法主要分为基于搜索、基于智能算法和基于采样的路径规划方法三类。基于搜索的路径规划方法包括Dijkstra方法、A*β方法等。文献[6]、文献[7]采用Dijkstra算法生成两台风电机组之间的最短路径,然后采用最小生成树方法连通所有道路,形成整个风电场的拓扑结构。文献[5]和文献[8]采用A*β方法对风电场道路进行优化设计,选线模型以曼哈顿距离为启发函数,以道路纵坡坡度、纵坡坡长、竖曲线转角等为约束条件。Dijkstra方法和A*β方法运用在山地风电场中,需要对地图进行网格化处理,网格的大小会影响优化的效率和计算的精度。A*β方法比Dijkstra方法多一个启发式函数,遍历的网格会更少,同样的条件下,A*β方法使用的时间更少。基于智能算法的路径规划方法包括遗传算法、蚁群算法等。这两种方法属于传统的启发式方法,在优化过程中一个显著问题是会产生局部最优,优化结果不是最佳的。基于采样的路径规划方法包括快速扩展随机树算法（rapidly exploring random tree, RRT）、RRT*β算法和informed RRT*β算法等。与Dijkstra和A*β等基于搜索的方法相比,这类方法可以在地图范围内随意采样,作为道路树发展的方向,不需要对地图进行网格处理,从而节约一部分网格处理的时间。
针对基于采样方法的优点,提出一种使用改进的RRT*β算法对陆上山地风电场道路路线进行优化设计的方法,通过参考风电场道路相关设计要求,将道路坡度和转弯半径等约束条件作为成本惩罚系数,利用改进的RRT*β算法优化得到风电场较合理的道路路线。
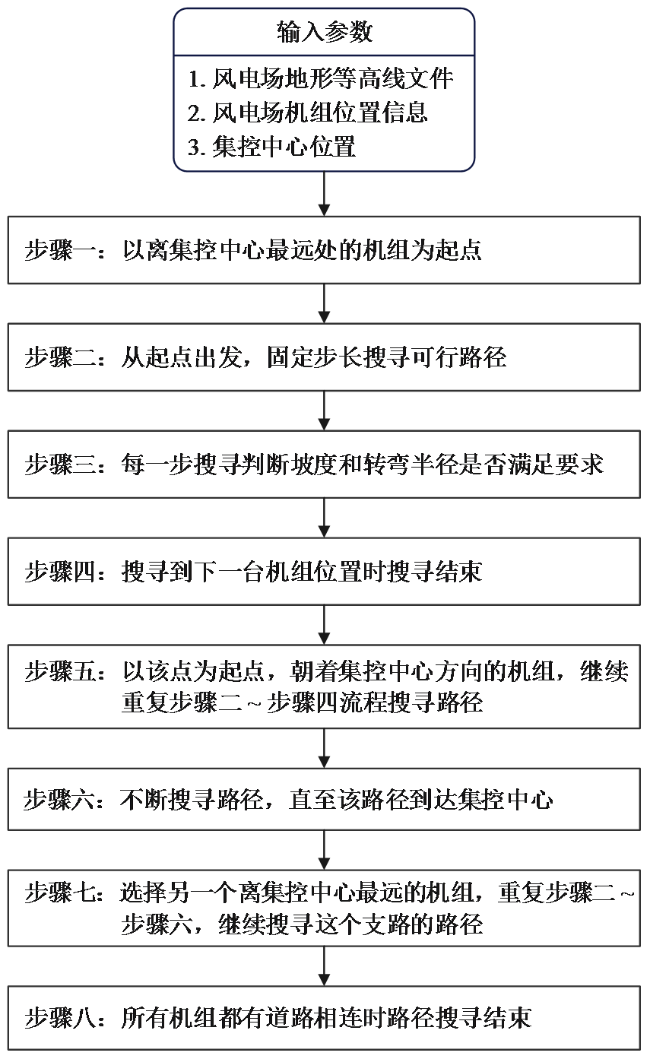
1 基于改进RRT*β算法的山地风电场路径优化算法
如图2所示,风电场道路的拓扑结构可以简化为一个风电机组作为顶点、机组之间的道路作为边的连通图$\mathbf{G}\left( \mathbf{T},\mathbf{E} \right)$。其中：
$\mathbf{T}=\left\{ {{T}_{1}},{{T}_{2}},\cdots ,{{T}_{i}},\cdots ,{{T}_{N}} \right\}$ (1)
$\begin{align}& \mathbf{E}=\left\{ {{E}_{1,2}},{{E}_{1,3}},\cdots ,{{E}_{i,j}},\cdots \right\} \\ & i,j\in \left\{ 1,2,\cdots ,N \right\},i\ne j \\ \end{align} $ (2)
${{E}_{i,j}}=\left\{ {{e}_{\text{star}}},{{e}_{1}},{{e}_{2}},...,{{e}_{k}},...,{{e}_{\text{end}}} \right\} $ (3)
式中：顶点集T代表风电机组;边集E代表风电场道路; $N $为风电场内机组数量;Ei,j为第i台和第j台风机之间的道路; ${{e}_{k}} $为道路的控制点; ${{e}_{\text{star}}} $、 ${{e}_{\text{end}}} $分别为道路起点和终点。以道路建设成本作为权重,采用改进RRT*β算法计算得到两台风机之间最优路径Ei,j,在此基础上使用最小生成树方法得到建设成本最低的道路方案。
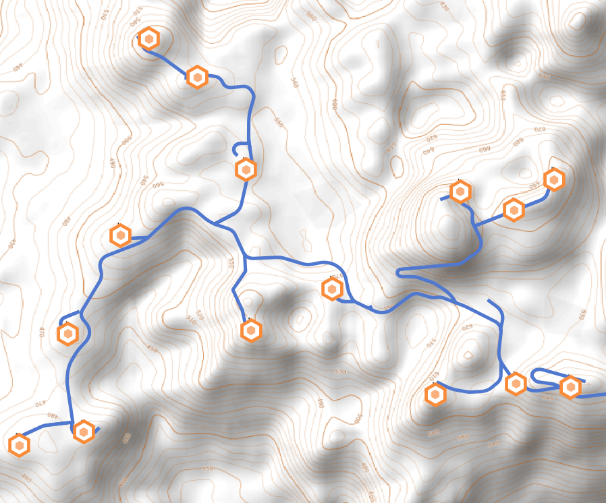
Fig. 2 The schematic diagram of wind farm road图2 风电场道路示意图 |
1.1 山地两点间距离计算
$|{{P}_{A}}{{P}_{B}}|=\sqrt{{{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}+{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}}} $ (4)
两点水平距离为：
$|{{P}_{A}}{{P}_{B}}{{|}_{\text{h}}}=\sqrt{{{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}} $ (5)
Fig. 3 Approximate calculation method of geodesic distance图3 测地线距离近似计算方法示意图 |
1.2 基于改进RRT*β的两点间最短路径优化方法
RRT算法[10,11]可以处理障碍物和差分约束（非完整和动力学）问题,但由于其采样的随机性,导致最终生成的路径往往只是可行路径而不是经过优化的路径。因此,KARAMAN等[12]提出了一种改进的RRT*β算法。RRT与Dijkstra算法区别在于,Dijkstra算法基于栅格,在栅格上一步步扩展;RRT是从根节点长出一棵树,当树枝长到终点时,就能找到一条从终点到根节点的唯一路径。在过去的研究中,RRT和RRT*β算法主要应用于机器人、无人机等的路径规划方面研究。这两种方法是基于采样的方法,可以相对快速地找到可行的运动路线。RRT*β是RRT的优化版本,RRT*β算法生成树的过程与RRT相似,RRT*β算法的改进主要有两点：①RRT*β在找到新节点之后,在与父节点连接时,会在一个范围内重新选择父节点,优化父节点到新节点的路径;②随机得到新节点如果在已经生成的树节点起始点侧,可以利用新节点优化已经生成的树,缩短新节点范围内树枝长度。
前人研究的RRT*β算法只运用在二维平面中。陆上山地风电场地形复杂,建设道路的限制因素有地形坡度和转弯半径,地形坡度应小于最大容许坡度值,转弯半径应大于最小的转弯半径。本文将RRT*β算法应用于三维地形上道路线路规划,同时通过道路坡度和转弯半径计入道路建设成本函数中,提出山地风电场改进RRT*β算法。
改进RRT*β算法的主要过程如下。
步骤一： ${{e}_{\text{star}}} $作为随机树的根节点。
步骤二：在整个地形图的范围内随机产生一个随机点 ${{N}_{\text{rand}}} $。
步骤三：找到树节点上距离随机点最近的点 ${{N}_{\text{near}}}({{x}_{\text{near}}},{{y}_{\text{near}}}) $。以 ${{N}_{\text{near}}} $为圆心做半径为 $\text{ }\!\!\Delta\!\!\text{ }l $的辅助圆,在辅助圆上等间距取M个备选点。第i个备选点坐标 $({{x}_{\text{alter}}},{{y}_{\text{alter}}}) $如下：
$\left\{ \begin{matrix} {{x}_{\text{alter}}}\left[ i \right]={{x}_{\text{near}}}+\Delta l\cos \left( \frac{2\text{ }\!\!\pi\!\!\text{ }i}{M} \right) \\ {{y}_{\text{alter}}}\left[ i \right]={{y}_{\text{near}}}+\Delta l\sin \left( \frac{2\text{ }\!\!\pi\!\!\text{ }i}{M} \right) \\\end{matrix} \right. $ (6)
式中：Δl为步进长度。备选点的高程 ${{z}_{\text{alter}}}[i] $通过对高程地图插值求得。
步骤四：计算各备选点的坡度 $\Delta S $和转弯半径 ${{R}_{\text{s}}} $。如图4所示,设 ${{N}_{\text{near}}} $的上游路径节点为 ${{N}_{\text{parent}}} $,对于折线 ${{N}_{\text{parent}}}\to {{N}_{\text{near}}}\to {{N}_{\text{alter}}} $,求其在 ${{N}_{\text{near}}} $的转弯半径时,可认为转弯圆弧与某一边的交点到 ${{N}_{\text{near}}} $的距离不超过该边长的一半。设 $\theta $为折线 ${{N}_{\text{parent}}}\to {{N}_{\text{near}}}\to {{N}_{\text{alter}}} $的夹角,则：
$\Delta S=\frac{\left| {{z}_{\text{alter}}}\left[ i \right]-{{z}_{\text{near}}} \right|}{\Delta l} $ (7)
${{R}_{\text{s}}}=\frac{1}{2}\min \left( {{l}_{\text{a}}},{{l}_{\text{b}}} \right)\tan \left( \frac{\theta }{2} \right) $ (8)
$\theta =\text{ }\!\!\pi\!\!\text{ }-\text{arc}\cos \left( \frac{{{l}_{\text{a}}}^{2}+{{l}_{\text{b}}}^{2}-{{l}_{\text{c}}}^{2}}{2{{l}_{\text{a}}}{{l}_{\text{b}}}} \right) $ (9)
式中： ${{l}_{\text{a}}}{{l}_{\text{b}}}{{l}_{\text{c}}} $分别为线段 ${{N}_{\text{parent}}}{{N}_{\text{near}}} $、 ${{N}_{\text{near}}}{{N}_{\text{alter}}} $、 ${{N}_{\text{parent}}}{{N}_{\text{alter}}} $的水平投影长度。
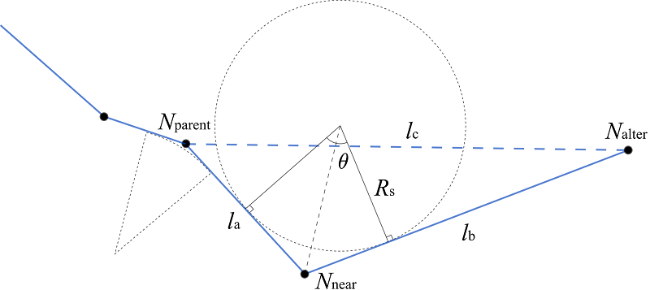
Fig. 4 Schematic diagram of the turning radius at the alternate point图4 备选点处的转弯半径示意图 |
步骤五：判断各备选节点是否满足坡度和转弯半径要求,并从所有满足要求的备选节点中选择到终点 ${{e}_{\text{end}}} $最近的备选点作为新节点 ${{e}_{k}} $。图5为随机树扩展过程中产生新节点 ${{e}_{k}} $的示意图,图中不同的颜色代表着等高线的高低不同,坐标值进行平移变换。
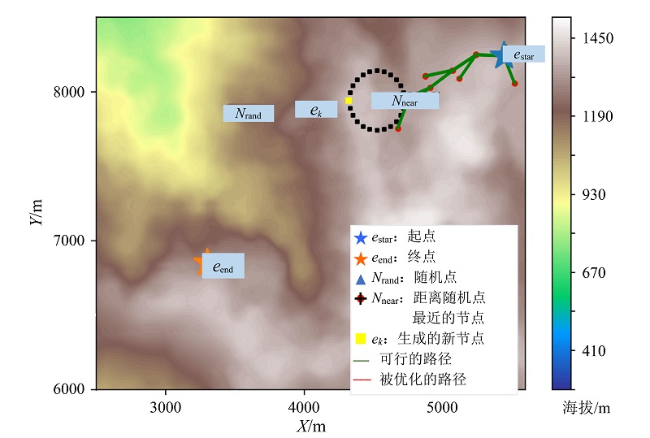
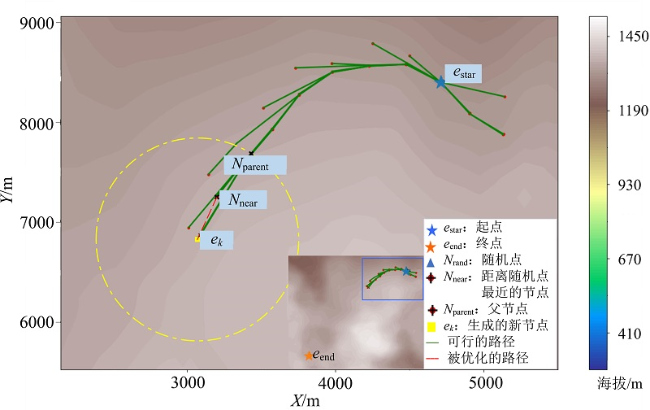
Fig. 5 Generating a new node ek by the improved RRT* method图5 使用改进RRT*β方法产生新节点ek |
步骤六：优化新节点 ${{e}_{k}} $的父节点。如图6所示,路径 ${{N}_{\text{parent}}}\to {{N}_{\text{near}}}\to {{e}_{k}} $是上一步骤四生成的路径,路径 ${{N}_{\text{parent}}}\to {{e}_{k}} $是优化后结果。在图6中,新节点 ${{e}_{k}} $的原父节点为 ${{N}_{\text{near}}} $,经过对新生成节点重新寻找其相邻节点的搜索作为父节点,新点 ${{N}_{\text{near}}} $的父节点变为节点 ${{N}_{\text{parent}}} $,路径为 ${{N}_{\text{parent}}}\to {{e}_{k}} $,显然路径长度缩短。
Fig. 6 Schematic diagram of new node ek reselecting parent node图6 新节点ek重新选择父节点示意图 |
步骤七：判断是否结束道路树生长。如果 ${{N}_{\text{near}}} $到终点 ${{e}_{\text{end}}} $的距离小于步进长度Δl,则把节点 ${{N}_{\text{near}}} $到终点 ${{e}_{\text{end}}} $连起来并更新随机树。进入步骤七,否则返回步骤二。
步骤八：从终点 ${{e}_{\text{end}}} $开始,逐步寻找节点的父节点,一直到随机树的根节点 ${{e}_{\text{star}}} $,返回最终的路径 ${{E}_{i,j}} $。如图7所示。
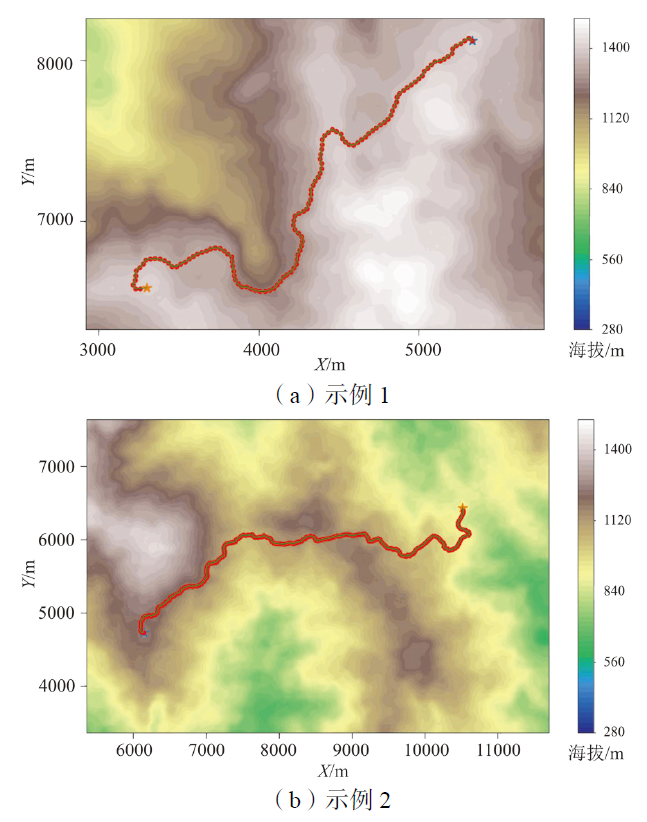
Fig. 7 The shortest feasible path between two points based on the improved RRT* algorithm图7 基于改进RRT*β算法的两点间最短可行路径 |
1.3 山地风电场道路建设成本模型
根据1.2节,可以得到风电场内部风电机组之间可行道路的连通图E,然后使用最小生成树方法得到风电场道路最短路径方案。具体如下：一个风电场有N台机组,则连通图E包含 $N\left( N-1 \right)/2 $条路径。连接N台风电机组至少需要 $N-1 $条路径。最小生成树方法要求连通路径的总权值最小,即得到风电场道路的优化方案。为了体现不同路段坡度和转弯半径对道路建设成本的影响,应先采用成本函数对不同路段进行成本计算,得到整条路的建设成本,以此作为边的权重。
风电场道路的成本与道路路径长度、道路的复杂程度正相关。在进行道路设计时,算法基于原始的地形进行道路设计,部分路段坡度或转弯半径超过限制范围时,需要对地形进行改造,增加土石方的挖方与填方的工程量。另一方面,如果改造后的坡度依然超过限制范围,在风电机组运输过程中需要增加额外的牵引车,增加额外的运输成本。因此坡度越大、转弯半径越小的路段,道路综合成本越高。为了降低风电场投资,风电场道路路径优化是以全场道路的建设成本最小为优化目标。道路建设成本函数C为：
$C=\sum\limits_{i=0}^{n}{{{l}_{i}}m{{s}_{i}}{{w}_{i,i+1}}} $ (10)
式中：n为道路分段数; ${{l}_{i}} $为i段路线的长度,m;m为道路的单位成本,元/m; ${{s}_{i}} $为i段路线的坡度成本惩罚系数; ${{w}_{i,i+1}} $为i段和i+1路线转弯半径的成本惩罚系数;最后一段道路没有转弯问题,其 ${{w}_{i,i+1}} $设为1。 ${{s}_{i}} $、 ${{w}_{i,i+1}} $的取值如表1所示。
Table1 Wind farm road cost penalty factor table表1 风电场道路成本惩罚系数表 |
| 道路坡度/% | ${{s}_{i}} $ | 道路转弯半径/m | ${{w}_{i,i+1}} $ |
|---|---|---|---|
| 0 ~ 12 | 1.0 | 35 | 5.0 |
| 13 ~ 15 | 1.5 | 40 | 2.0 |
| 16 ~ 19 | 5.0 | 45 | 1.5 |
| ≥20 | 50.0 | ≥50 | 1.0 |
因此每一条道路的建设成本可以表示为：
${{W}_{i,j}}=\sum\limits_{k=0}^{n}{|{{e}_{k+1}}{{e}_{k}}|\cdot m\cdot {{s}_{k}}\cdot {{w}_{k,k+1}}} $ (11)
通过式（11）计算连通图E中路径之间的道路建设成本,得到路径建设成本的连通图W：
$\begin{align} & \mathbf{W}=\left\{ {{W}_{1,2}},{{W}_{1,3}},\cdots ,{{W}_{i,j}},\cdots \right\}, \\ & i,j\in \left\{ 1,2,\cdots ,N \right\},i\ne j \end{align} $ (12)
然后采用最小生成树算法,计算出连通图W的权值最小的方案 ${{\mathbf{G}}_{\min }}\left( \mathbf{T},\mathbf{W} \right) $,即为风电场道路建设成本最低的方案。
2 结果与讨论
2.1 实验风电场参数
Table 2 Parameters of wind farms表2 实验风电场参数 |
| 风电场名称 | 风电场位置 | 机组数量/台 | 风电场平均高程/m | 风电机组单机容量/MW | 道路设计容许坡度/% |
|---|---|---|---|---|---|
| 风电场1 | 福建龙岩 | 24 | 1 235 | 2.0 | 10.82 |
| 风电场2 | 河南南阳 | 20 | 550 | 2.5 | 9.54 |
| 风电场3 | 河南平顶山 | 11 | 680 | 4.5 | 7.50 |
2.2 实验风电场道路路线优化
实验采用的数字高程地图精度为12.5 m,改进的RRT*β算法的步进长度Δl取值由多次试验确定。当步进长度取值为10 ~ 20 m时,算法会因局部地形突起导致路径弯道较多。当步进长度取值大于50 m,计算的精度减小,与实际对比误差较大。为保证计算精度和道路的平滑,步进长度Δl设为30 m。实验风电场中改进的RRT*β算法的参数如表3所示。
Table 3 Parameters of the improved RRT* algorithm表3 改进RRT*β算法的参数 |
| 参数/单位 | 数值 |
|---|---|
| 备选点M | 100 |
| 步进长度Δl/m | 30 |
| 转弯半径最小值 ${{R}_{\text{s,min}}} $/m | 35 |
实验中根据道路建设成本函数,计算每一条路线的建设成本。最后以每条路的建设成本为权值,采用最小生成树方法生成风电场道路建设成本最低的方案,并计算出道路的总建设成本。3个风电场的算法优化方案如图8所示。
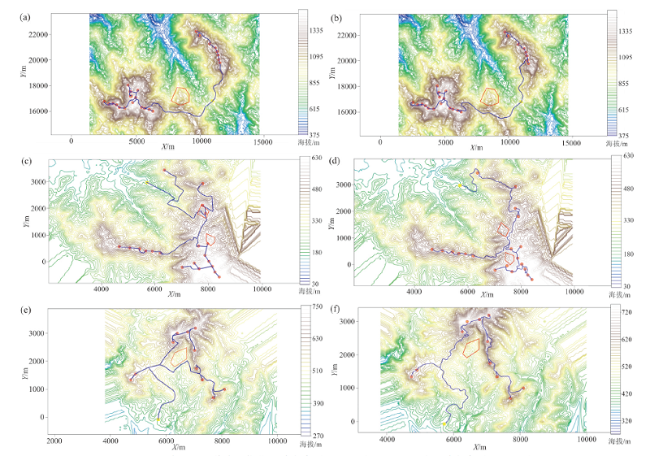
Fig. 8 Algorithm optimization design scheme (a, c, e) and artificial experience design scheme (b, d, f) for road of wind farm 1-3图8 风电场1 ~ 3道路的优化设计方案（a、c、e）和人工经验设计方案（b、d、f） |
2.3 优化结果与分析
Fig. 9 The methods for designing wind farm roads with experience图9 人工经验设计风电场道路的方法 |
Table 4 Road cost calculation table of wind farm 1-3表4 风电场1 ~ 3道路成本计算表 |
| 方案类型 | 道路总长度/km | 最大坡度/% | 改造路段/km | 优化时间 | 道路成本/万元 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 风电场1 | 风电场2 | 风电场3 | 风电场1 | 风电场2 | 风电场3 | 风电场1 | 风电场2 | 风电场3 | 风电场1 | 风电场2 | 风电场3 | 风电场1 | 风电场2 | 风电场3 | |||||
| 人工经验 | 24.822 | 18.576 | 14.668 | 40.08 | 55.38 | 50.07 | 2.86 | 1.56 | 1.75 | 3 h | 2.5 h | 1.5 h | 1 305.92 | 865.37 | 793.42 | ||||
| 算法优化 | 25.341 | 19.781 | 15.654 | 33.14 | 32.88 | 36.84 | 2.05 | 1.08 | 1.39 | 56 s | 48 s | 30 s | 1 282.52 | 799.53 | 734.23 | ||||
| 变化量 | ↑2.09% | ↑6.48% | ↑6.72% | ↓17.3% | ↓40.63% | ↓26.425 | ↓28.32% | ↓30.77% | ↓20.57% | — | — | — | ↓8.79% | ↓7.61% | ↓7.46% | ||||
注：改造路段表示这个路段的坡度超过容许坡度,需要进行地形改造,进行大量土方挖填。 |
风电场1地形最复杂,场址范围内高程差达到700 m,且机组位于两条不连接的山梁上。算法优化方案的道路总长度比人工经验设计方案多出2.09%,但是由于算法对陡坡路段控制较好,使得道路经过的陡坡路段少,需要进行道路改造的工程量减少,且最大坡度小于人工方案,使得道路成本下降了8.79%。风电场2机组布局紧凑,算法设计方案避开了陡坡路段,选择从其他方向走线,促使案例中算法计算的最大坡度比人工方案小40.63%。风电场3机组和升压站位置分布松散,机组数量比风电场2少近50%,但是道路总长度仅减少了20%左右,其计算结果变化特征和上面两个风电场相似。
在上述风电场中,为了降低大纵坡引起的土方量增多,优化算法采用了适当增加路径长度避开大纵坡的策略,使得道路最大坡度和需要改造的路段都明显小于人工经验设计方案,从而降低道路建设成本。通过比较优化方案和人工经验设计方案,优化结果在道路坡度控制、道路建设成本上都优于人工经验设计方案。
此外,在利用人工经验设计道路方案过程中,存在工作效率较低、耗时长、修改不便等缺点。而优化算法采用计算机进行自动寻优,计算效率极大地提升,节省大量时间,对地形复杂或存在大量机位的陆上风电场优势更加显著。
3 结论
（1）改进RRT*β算法在风电场道路优化方面取得了较好结果,可以在道路坡度、转弯半径的限制下找到优化的可行道路。经过3个风电场测试,基于改进RRT*β算法道路设计方案结果优于人工经验设计方案,能够显著提升设计效率。
（2）提出的风电场道路建设成本函数将道路坡度和转弯半径作为惩罚系数,坡度越大、转弯半径越小,惩罚系数越大,得到的道路建设成本越高。经过案例测试,该函数可以有效控制道路坡度,进而减少道路的建设成本。
（3）提出的基于改进RRT*β算法道路路线优化设计方案仅适用于风电场道路前期可研阶段,生成道路的路线方案,并没有对道路桩点、路面剖面等进行详细设计。该方法的优势是可以快速生成陆上山地风电场内可行的优化路径,提高设计效率,对工程设计有一定参考价值。