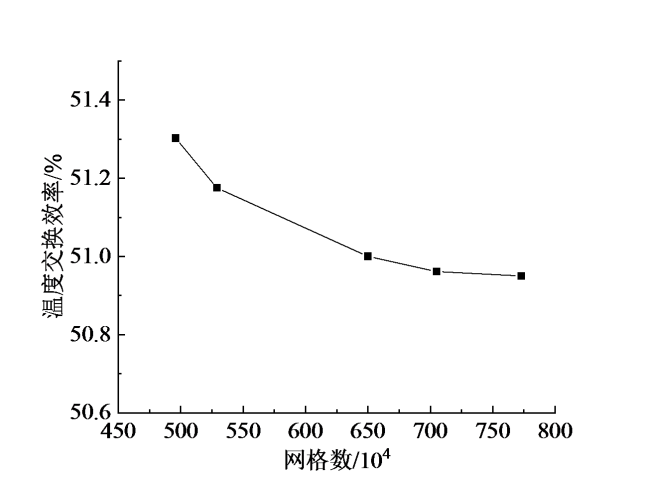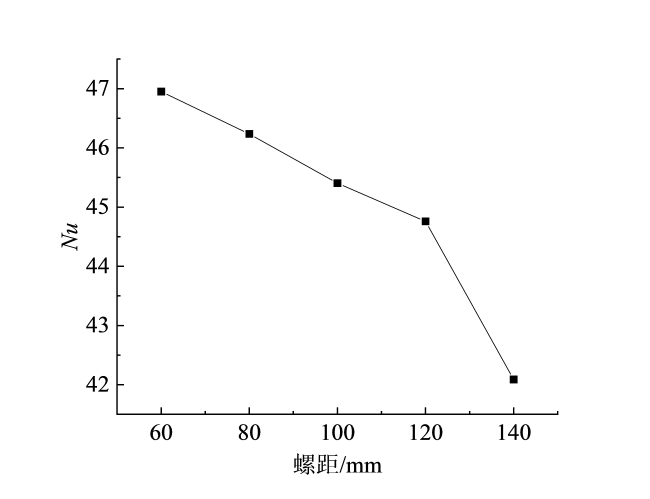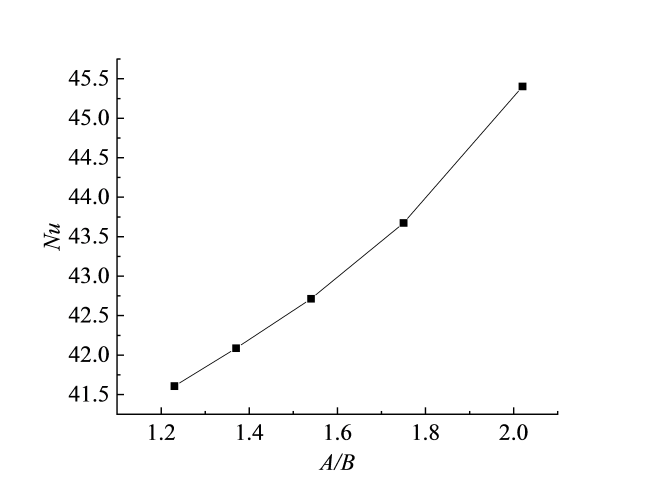0 引言
本文以椭圆扭曲管作为换热元件设计一种应用于空调新风系统室内能量回收的椭圆扭曲管能量回收器,借助数值模拟的方法对空气作为工质的换热与阻力特性进行研究。分析不同几何参数对椭圆扭曲管能量回收器换热与阻力的影响,并对其节能效果进行研究,研究结果可为椭圆扭曲管能量回收器的工程应用提供一定参考。
1 高效能量回收器强化传热机理
椭圆扭曲管是一种特殊的换热器,采用传统的光滑圆管在进行冷轧和扭曲加工后生产而成。换热管的横截面呈椭圆状,其两端在制造加工过程中保持圆形,以便更好地与管板进行组装,其结构示意图如图1所示,其中,A表示长轴,B表示短轴,P表示螺距。
Fig. 1 Schematic diagram of elliptical twisted tube structure图1 椭圆扭曲管结构示意图 |
Fig. 2 Self-supporting schematic diagram of elliptical twisted tube图2 椭圆扭曲管自支撑示意图 |
椭圆扭曲管的特殊外形结构和椭圆扭曲管高效能量回收器特殊的制造与组装过程,使得管内外形成了特殊的通道。流体在管内外循环时,产生以旋转为主要特征的复杂流动,并且在管内垂直于主流的方向上产生了二次流,从而达到了促进换热的目的;当流体受到管内外侧的离心力影响时,又可周期性地改变流向和流速,从而增强了其自身的湍流性,在管内外形成了剧烈的流体扰动,有助于破坏管壁上的热边界层,同时强化管内外换热效果[10]。
椭圆扭曲管能量回收器物理模型如图3所示,能量回收器长700 mm、宽120 mm、高36 mm,由30支椭圆扭曲管组成,分为3排,每排10支。室内回风在椭圆扭曲管管内流动,走管程;室外新风在椭圆扭曲管管间流动,走壳程。采用超薄铝合金作为椭圆扭曲管材料,塑料作为壳体材料。
Fig. 3 Elliptical twisted tube energy recovery device model图3 椭圆扭曲管能量回收器模型 |
2 数值模拟
2.1 物理模型
为了简化模型,将高效能量回收器中的30支椭圆扭曲管简化为9支,一共3排,每排3支。所用椭圆扭曲管均采用D 10 mm × 0.4 mm的圆管通过压扁螺旋扭转形成。建立9种不同的椭圆扭曲管的物理模型和相应的圆管模型,具体结构尺寸见表1。
Table 1 Geometric parameters of energy recovery device表1 能量回收器几何参数 |
| 模型编号 | A/mm | B/mm | P/mm |
|---|---|---|---|
| 1 | — | — | — |
| 2 | 12.0 | 7.77 | 60 |
| 3 | 12.0 | 7.77 | 80 |
| 4 | 12.0 | 7.77 | 100 |
| 5 | 12.0 | 7.77 | 120 |
| 6 | 12.0 | 7.77 | 140 |
| 7 | 13.0 | 6.44 | 120 |
| 8 | 12.5 | 7.13 | 120 |
| 9 | 11.5 | 8.38 | 120 |
| 10 | 11.0 | 8.95 | 120 |
注：模型1为圆管模型。 |
2.2 数学模型
质量守恒方程：
$\frac{\partial \left( \rho u \right)}{\partial t}+\text{div}\left( \rho u \right)=0$ (1)
动量守恒方程：
$\frac{\partial }{\partial t}\left( \rho {{u}_{i}} \right)+\frac{\partial }{\partial {{x}_{j}}}\left( \rho {{u}_{i}}{{u}_{j}} \right)=-\frac{\partial p}{\partial {{x}_{i}}}+\frac{\partial {{\tau }_{ij}}}{\partial {{x}_{j}}}+\rho {{g}_{i}}+{{F}_{i}}$ (2)
应力张量由下式给出：
${{\tau }_{ij}}=\left[ \mu \left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial xi} \right) \right]-\frac{2}{3}\mu \frac{\partial {{u}_{l}}}{\partial {{x}_{l}}}{{\delta }_{ij}}$ (3)
能量守恒方程：
$\frac{\partial \left( \rho T \right)}{\partial t}+\text{div}\left( \rho uT \right)=\text{div}\left( \frac{K}{{{c}_{p}}}\text{grad}T \right)+{{S}_{T}}$ (4)
式中：ρ为流体密度;u为流体速度;t为单位时间;x表示x轴;p为静压;μ为流体动力黏度;i,j,l表示方向;$\tau_{ij}$为应力张量;gi和Fi分别为i方向上的重力体积力和外部体积力;cp为流体比热容;T为温度;K为流体的换热系数;ST为黏性耗散项。
2.3 边界条件设置及网格划分
对模型进行结构化网格划分,对近壁面附近区域进行局部加密,以保证在近壁面处的计算精度及对流动界面的准确捕捉,从而保证计算结果的精度[10]。
2.4 网格独立性验证
为保证数值计算结果的精确程度和计算残差的收敛性,同时节约计算资源,对模型进行网格无关性验证。能量回收器温度交换效率是一个很重要的参数,表征了换热效果的好坏,其计算公式如下：
${{\eta }_{\text{wd}}}\text{=}\frac{{{T}_{\text{xj}}}-{{T}_{\text{xc}}}}{{{T}_{\text{xj}}}-{{T}_{\text{pj}}}}\times 100\text{ }\!\!%\!\!\text{ }$ (5)
式中：$\eta_{wd}$为温度交换效率;Txj为新风进风干球温度,℃;Txc为新风出风干球温度,℃;Tpj为排风进风干球温度,℃。
故在进行网格无关性验证时,以能量回收器温度交换效率为研究对象,研究网格数量变化对能量回收器温度交换效率的影响,力求达到条件允许范围内的最佳网格数量,即网格数量的增加不再引起能量回收器温度交换效率的大幅变化。由图4可知,随着网格数量的增多,椭圆扭曲管能量回收器温度交换效率减小,但其减小趋势逐渐变缓,当网格数量为6.5 × 106时,温度交换效率变化较小,为了在满足精度条件下提高效率,将该模型的网格数量确定为6.5 × 106。
Fig. 4 Variation of temperature exchange efficiency with the number of grids图4 温度交换效率随网格数量的变化 |
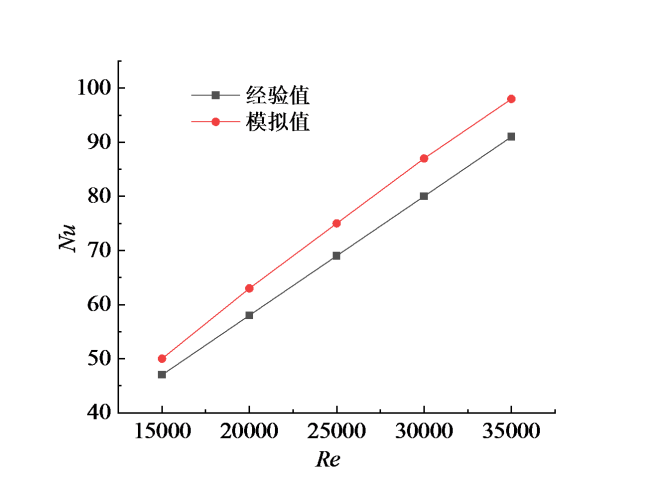
2.5 模拟结果可靠性分析
为了保证物理模型的可靠性,对圆管进行数值模拟,将所得结果与Dittus-Boelter经验值（$Nu=0.023R{{e}^{0.8}}P{{r}^{0.33}}$）进行对比。从图5可以看出,两者计算结果接近,偏差为6.8%,在误差允许范围内,证明了该计算模型是可靠的。
Fig. 5 Comparison of simulation value and empirical value of Nusselt number Nu图5 努塞尔数Nu模拟值与经验值计算对比 |
3 结果与分析
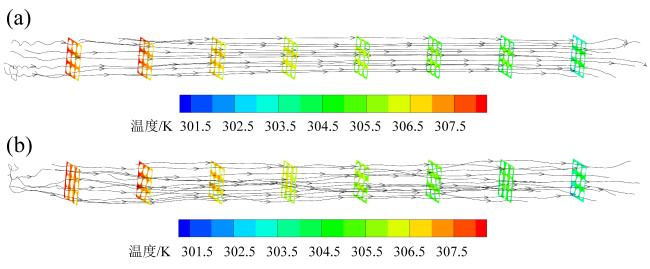
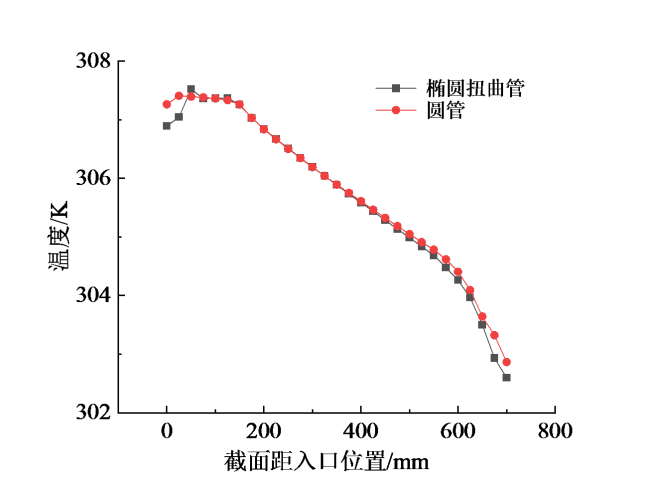
3.1 强化换热效果分析
图6为圆管和椭圆扭曲管能量回收器壳程流线分布图,以等距离选取若干截面,截面为温度分布图。此处的椭圆扭曲管能量回收器螺距P = 120 mm,长短轴比A/B = 1.54。在圆管能量回收器壳程流道内,空气流线基本为平行流状态,除壳程进出口附近,基本没有垂直于主流方向上的扰流。而在椭圆扭曲管能量回收器壳程流道内,流线的扰动非常明显,空气呈现出沿着椭圆扭曲管壁面的螺旋流,螺旋流的存在使椭圆扭曲管能量回收器的空气流动状态发生了较大的改变,不仅造成了空气在垂直于主流方向上剧烈的混合扰动,而且形成了对椭圆扭曲管壁面的冲刷作用,扰动了热边界层,增强了换热效果。
Fig. 6 Streamline distribution of shell side of energy recovery device with circular tube (a) and elliptical twisted tube (b)图6 圆管（a）和椭圆扭曲管（b）能量回收器壳程流线分布图 |
图7为空气进入两种能量回收器壳程后沿着管长方向上的温度变化对比。其中,沿z轴方向0 ~ 150 mm及550 ~ 700 mm为壳程流体进出口段。图中可见,空气在两种能量回收器壳程的温度变化趋势基本相同,但在椭圆扭曲管能量回收器内温度变化斜率更大。其中,椭圆扭曲管能量回收器在壳程入口处温度波动较大,两种能量回收器在出口处的温度分布未见明显区别,可以看出椭圆扭曲管能量回收器要发挥其换热优势需要一定的有效换热长度;而沿z轴方向350 mm处截面之后,椭圆扭曲管能量回收器壳程的温度一直低于圆管能量回收器壳程内的空气温度,说明椭圆扭曲管能量回收器的壳程温度下降更快,在相同的壁温和入口温度的条件下,椭圆扭曲管能量回收器可以将壳程内的空气降至更低的温度,达到更好的换热效果。
Fig. 7 Comparison of temperature changes along the tube length after air enters the shell side of two kinds of energy recovery device图7 空气进入两种能量回收器壳程后沿着管长方向上的温度变化对比 |
图8为空气进入两种能量回收器壳程后沿着管长方向上的速度变化对比。图中可见,两种不同管型的能量回收器的纵向速度变化整体趋势相同。在壳程入口附近处速度迅速上升,在壳程出口处速度迅速下降,其中由于椭圆扭曲管管型结构特点,其速度变化相对圆管存在一定的波动。椭圆扭曲管壳程流通面积大于圆管壳程流通面积,在一定的质量流量下,椭圆扭曲管平均速度略小于圆管。沿z轴方向150 ~ 550 mm处,椭圆扭曲管能量回收器在螺旋流的作用下,平均速度沿管长方向有轻微的波动,呈波浪型,而圆管能量回收器内流体速度非常稳定,呈一条直线。
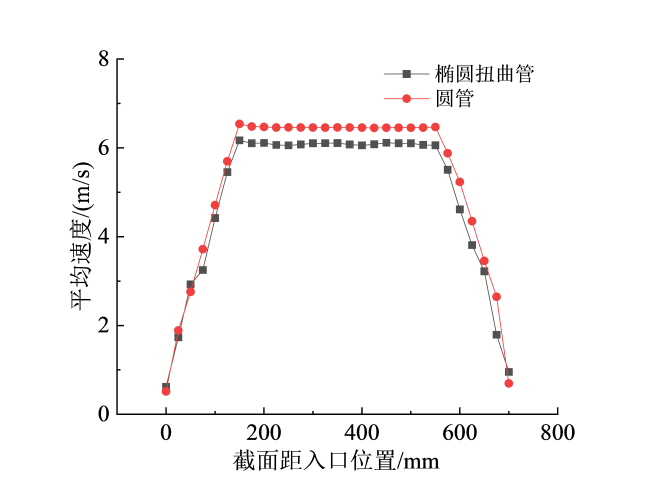
Fig. 8 Comparison of velocity changes along the tube length after air enters the shell side of two kinds of energy recovery device图8 空气进入两种能量回收器壳程后沿着管长方向上的速度变化对比 |
3.2 几何参数对换热性能的影响
3.2.1 螺距对换热与阻力的影响
图9显示了不同螺距对椭圆扭曲管能量回收器壳程和管程温度特征的影响。对比发现,P = 60 mm的椭圆扭曲管能量回收器的螺旋流对管壁的冲刷作用更强,而当流体绕过长轴凸点后,脱离管壁的脱体现象更强烈,椭圆形截面一侧温度较高而另一侧温度较低的现象也更明显。对比发现,沿壳程空气流动方向任一截面上,P = 60 mm的壳程温度更低,管程则与之相反。整体换热效果随着螺距的减小而增强。
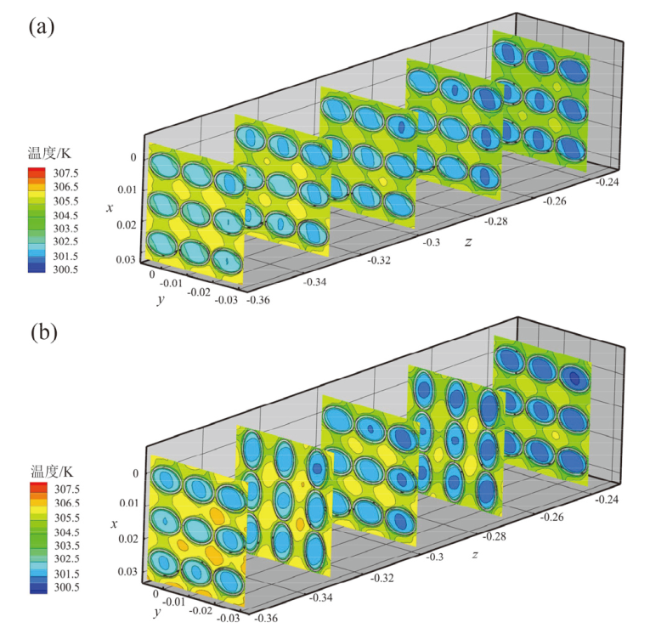
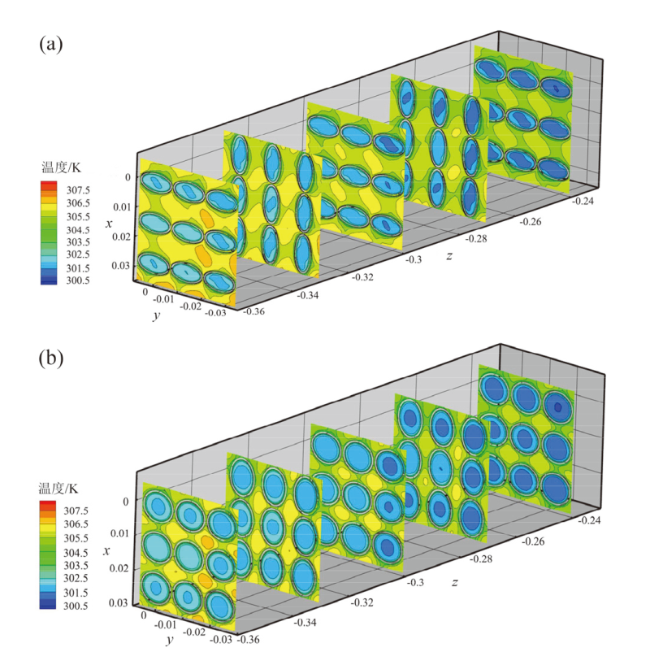
Fig. 9 Temperature distribution characteristics of elliptical twisted tube energy recovery device under different pitches: (a) P = 60 mm; (b) P = 120 mm图9 不同螺距下椭圆扭曲管能量回收器温度分布特点：（a）P = 60 mm;（b）P = 120 mm |
图10为壳程Nu随螺距的变化曲线。图中可见,椭圆扭曲管能量回收器壳程Nu随着螺距的增大而减小,而且随着螺距的继续增大,Nu下降的趋势也在增大。显然减小螺距可以提高Nu,有利于壳程换热系数的提高。这是由于椭圆扭曲管螺距越小,单位长度的椭圆扭曲管扭转圈数越多,流体环绕管壁运动的圈数越多,流体的翻转次数也越多。流体在流动过程中,靠近管壁的流体和主流方向的流体由于多次的翻转造成充分混合,提高了换热系数。此外,流体翻转次数越多,需要克服更多的阻力,因此压降随之增加。
Fig. 10 Variation curve of Nu of shell side with pitch图10 壳程Nu随螺距的变化曲线 |
图11为不同螺距下壳程和管程压降Δp随体积流量的变化曲线。由图可知,随着体积流量增大,Δp也随之增大。在同等体积流量的前提下,椭圆扭曲管能量回收器Δp总是大于圆管能量回收器的,P越小,Δp受到体积流量的影响就越大。流速较低时,Δp变化缓慢,但当流速增大时,速度的增大导致阻力增大,因此Δp明显增大。
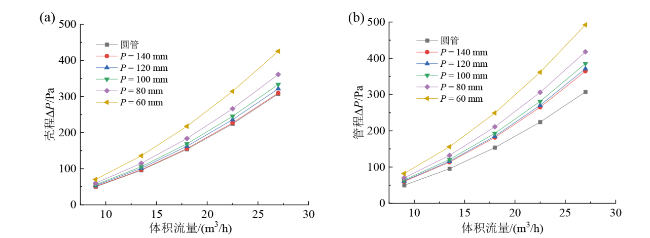
Fig. 11 Variation curve of shell side (a) and tube side (b) pressure drop with volume flow rate under different pitches图11 不同螺距下壳程（a）和管程（b）压降随体积流量的变化曲线 |
图12为不同螺距下能量回收器的换热系数随体积流量的变化曲线,图中可见,不同管束布置的K随着体积流量的增大而增大。椭圆扭曲管能量回收器的K总是大于圆管能量回收器,但是随着P的增大,K不断减小。
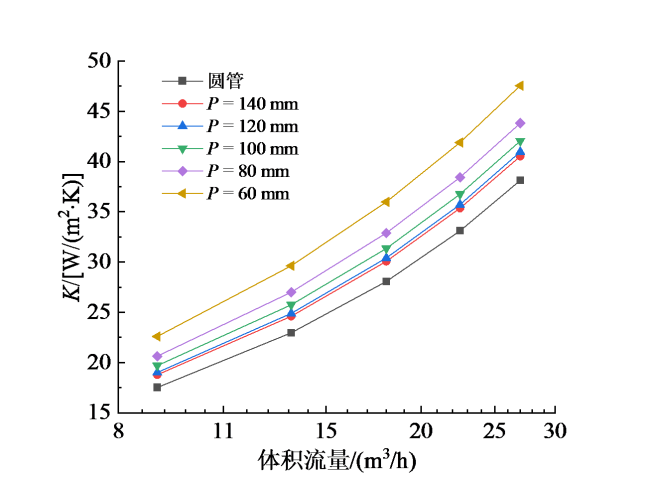
Fig. 12 Variation curve of heat transfer coefficient K of energy recovery device with volume flow rate under different pitches图12 不同螺距下能量回收器的换热系数K随体积流量的变化曲线 |
3.2.2 长短轴比对换热与阻力的影响
图13展示了长短轴比（A/B）对椭圆扭曲管能量回收器壳程和管程温度特征的影响。从图中可知,壳程流道内螺旋流随着A/B的增大而加强。当流体经过A/B = 2.02的椭圆扭曲管能量回收器截面椭圆形的长轴凸点时,边界层受到剧烈的扰动,流体间产生强烈的径向混合,但由于其长轴过长,导致由长轴凸点相连的椭圆扭曲管能量回收器的壳程流通面积增大,平均流速降低,整体换热效果不如A/B = 1.23的椭圆扭曲管能量回收器。而A/B = 1.23的能量回收器由于壳程流通面积过小导致壳程平均流速过高,产生的壳程压降较大。
Fig. 13 Temperature distribution characteristics of elliptical twisted tube energy recovery device with different long-short axis ratios: (a) A/B = 2.02; (b) A/B = 1.23图13 不同长短轴比时椭圆扭曲管能量回收器温度分布特点：（a）A/B = 2.02;（b）A/B = 1.23 |
图14为壳程Nu随长短轴比的变化曲线。随着A/B的增加,Nu也在不断增大。A/B越大,代表换热管压扁程度越大,管内当量直径de越小,流体以同样的速度沿壁面流过受到的向心力就越大;转过凸点位置之后,沿着凸点处的切线方向脱离壁面时的离心力就越大,螺旋流对周围的流体的扰动就更加强烈,即管内流体的速度场和温度场扭曲程度加剧,换热效果增强。增强的螺旋流对于流体主流方向上的流动也形成了更大阻力,因此流体压降也随之升高。
Fig. 14 Variation curve of Nu of shell side with long-short axis ratio图14 壳程Nu随长短轴比的变化曲线 |
图15为不同长短轴比时壳程、管程压降随体积流量的变化曲线。从图中可以看出,随着体积流量的增加,Δp也随之增加。而长短轴比A/B数值越小时,壳程Δp就越大,管程Δp越小。
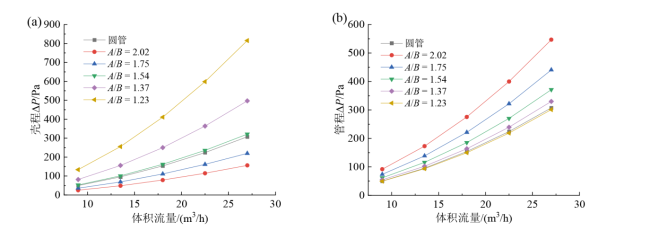
Fig. 15 Variation curve of shell side (a) and tube side (b) pressure drop with volume flow rate at different long-short axis ratios图15 不同长短轴比时壳程（a）和管程（b）压降随体积流量的变化曲线 |
图16为K随长短轴比A/B变化的性能曲线,从图中可以看出,以椭圆扭曲管布置的高效能量回收器K总是大于圆管,随着长短轴比A/B值的增大,K不断减小。
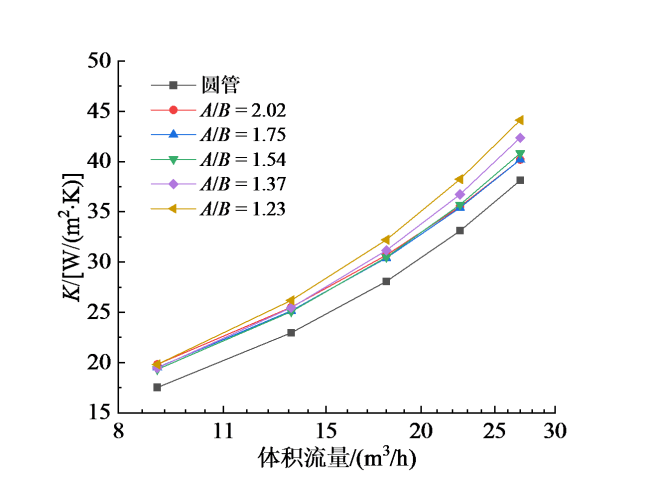
Fig. 16 Variation curve of heat transfer coefficient with volume flow rate at different long-short axis ratios图16 不同长短轴比时换热系数随体积流量的变化曲线 |
4 节能性分析
当前市场上大多数新风系统通过“纸芯”交换器进行热回收,换热器的表面孔隙率直径大于100 nm,远大于病毒尺寸,没有防疫功能,容易让新风与回风交叉污染;病毒会通过回风回路渗透到新风回路回到原房间,甚至有可能流向到其他房间。并且由于没有能量回收装置,导致空调系统能耗增加,对能源造成极大浪费。
分析了不同几何参数对椭圆扭曲管能量回收器换热与阻力的影响,选取符合当前需求的参数,将基于椭圆扭曲管的新型能量回收器应用于空调新风系统,研制出新风机样机,力求实现建筑低碳节能需求。
选择广州、武汉和北京三个典型城市,分别代表夏热冬暖地区、夏热冬冷地区和寒冷地区,以一套室内建筑面积为86 m2左右的三居室作为研究对象来测算全年节能量,其空间体积约240 m3。新风机的室内排风进风温度分别取27 ℃（夏季）和21 ℃（冬季）。
采用温频法计算全年热回收节能收益,计算公式如下：
${{E}_{\text{ay}}}=\beta \left[ \sum\limits_{i=1}^{n}{\frac{{{m}_{\text{xj}}}c{{A}_{\text{bj}}}\left( {{T}_{x\text{j}-i}}-{{T}_{\text{xc}-i}} \right){{h}_{i}}}{{{\varepsilon }_{i}}}-{{w}_{\text{ex}}}{{h}_{\text{ay}}}} \right]$ (6)
式中：Eay为对排风能量进行回收节约的空调和热泵机组年电耗量,kW∙h;Txj-i、Txc-i为新风进出口温度,℃;mxj为新风质量流量,kg/s;c为空气比热,kJ/(kg∙℃);hi为新风进风温度为Txj-i的运行时数,h;εi为新风进风温度为Txj-i的空调或热泵机组系统能效;wex为新风与排风阻力的折算功耗,W;hay为年运行时数,取8 760 h;β为年运行率,按照经验值取0.7。
Table 2 Comparison of annual energy saving benefits of ventilator energy recovery in three typical cities表2 三个典型城市的新风能量回收年节能收益对比 |
| 典型城市 | 总节能收益/(kW∙h) | 能量回收季节能收益/(kW∙h) | 计算节能收益总时数/h | 计算节能收益的时数比例/% |
|---|---|---|---|---|
| 广州 | 96.57 | 191.96 | 3 750 | 42.81 |
| 武汉 | 523.21 | 603.50 | 4 543 | 51.86 |
| 北京 | 860.87 | 943.02 | 4 445 | 50.74 |
由上表可知,新风能量回收年节能收益在北京地区最高,武汉次之,而广州地区远低于前两个典型城市,分别仅为北京的11.22%和武汉的18.46%。分析其原因,一是广州地区全年计算节能收益的时数占比明显少于其他两座城市（计算节能收益的时数仅占新风机总运行时数的42.81%）;二是广州全年主要是制冷回收模式的节能收益,而节能收益更高的供热回收模式运行时数较少,且由于室外温度较高,热量回收量相对其他两个城市大大减少。
5 结论
通过Fluent软件研究椭圆扭曲管能量回收器的强化换热与流动特性,分析换热系数、压降在不同螺距、长短轴比下受到的不同影响,并进行节能性分析,得出以下结论：
（1）椭圆扭曲管能量回收器壳程流体的螺旋流动所形成的二次流增加了与空气的径向混合,从而增加了管内流体的湍流程度,并有效破坏了换热边界层,进而提高了空气换热效率;与圆管能量回收器相比,空气在椭圆扭曲能量回收器内壳程温度下降更快,管程温度提升也更快,换热系数更高。
（2）空气在椭圆扭曲管的换热系数K与长短轴比A/B和螺距P呈负相关;而壳程压降Δp、努塞尔数Nu随着螺距P的增大而减小,随着长短轴比A/B的增大而增大;管程压降Δp随着螺距P的增大而减小,随着长短轴比A/B的增大而减小。相同体积流量下,随着螺距的增大,Nu不断减小;而随着长短轴比的增大,Nu不断增大。
（3）增加能量回收器的新风机可以提升室内环境的舒适性,在夏热冬冷和寒冷地区节能效果非常明显,而在夏热冬暖地区,由于全年供热期很短,过渡季时数较长,且能量回收时数相对较短,节能效果并不显著。
（4）椭圆扭曲管能量回收器要发挥其换热优势需要一定的有效换热长度,具体的换热长度多少为宜可作为下一步的研究方向。