0 引言
与其他储能形式相比,压缩空气储能（compressed air energy storage, CAES）具有寿命长、环保、成本低以及储能时间长等优点[2]。但CAES响应时间长、经济效益低,影响其商业化推广及应用。为了缩短CAES的响应时间,提高经济效益,ZHAO等[3]设计一种由CAES和飞轮储能组成的混合储能系统,仿真结果表明,混合储能系统能较好地满足负荷需求,提高风电的渗透率;JIANG等[4]提出一种由CAES和超级电容器组成的混合储能系统,结果表明该系统既能发挥出CAES容量大的优势又能弥补CAES响应时间长的劣势。上述研究中飞轮储能和超级电容储能虽然能缓解CAES响应时间长的问题,但两者放电时间较短（秒-分钟）,而液流电池和两者相比,不仅响应时间和功率相同,且放电时长为小时级[2],更有利于储能系统稳定性。齐晓光等[5]提出一种CAES和液流电池组成的混合储能系统,结果表明该系统不仅能缩短储能系统响应时间,也能满足电网多性能需求。但上述模型对经济性的考虑较少。
为了缩短CAES系统响应时间,提高系统经济性,提出一种由液流电池与CAES组成的混合储能系统。在此基础上考虑风电与光伏不确定性对CAES系统规模优化配置的影响,并基于风电、光伏及负荷需求的典型周数据进行算例分析,验证优化模型的可靠性。
1 系统构成
风电耦合混合储能系统由风电场、光伏电站、电网、等压绝热压缩空气储能系统（isothermal adiabatic compressed air energy storage system, IA-CAES）、液流电池、负荷需求中心等组成,其结构示意图见图1。
Fig. 1 Structure diagram of grid-connected wind-coupled hybrid energy storage system图1 并网型风光耦合混合储能系统结构示意图 |
Fig. 2 Structure of IA-CAES图2 IA-CAES示意图 |
混合储能系统运行策略如图3所示,以充电为例,在t时刻当负荷需求功率PB小于风电场功率PWt与光伏电站功率PPv时,系统会计算出CAES和液流电池在t0（t0 = 3 600 s）时间内充电达到容量上限所需功率分别为Pca和Pfb,Δt1和Δt2分别为达到CAES额定转速和额定功率所用时间,t1和t2分别为达到CAES所需转速和功率所用时间;PCAES、PCra和CCra和分别为CAES的实时功率、额定功率和额定容量;PFra和CFra和分别为液流电池的额定功率和额定容量;tmax为仿真最长时间;ΔP为CAES启动阶段1秒中功率变化值;容量上限和下限分别为0.9和0.1。CAES充电主要有三种工况：工况1,当压缩机未到达所需转速时,仅液流电池工作,工作功率为P1,弃电功率为 |P1-PD|;工况2,当压缩机到达所需转速且未到达所需功率P2时,液流电池与CAES同时工作,液流电池与CAES工作功率分别为P1和PCAES,弃电功率为 |P1+PCAES-PD|;工况3,当压缩机到P2时,仅CAES工作,工作功率为P2,弃电功率为 |P2-PD|。
Fig. 3 Operation strategy diagram of hybrid energy storage system图3 混合储能系统运行策略图 |
为了简化系统工作过程数学模型,做如下假设：在各环节气体流通中不考虑漏气;忽略流体在流动和换热过程中的变化及化学反应;不考虑流体在管道中的热量损失和压力损失;IA-CAES的转速与功率为线性关系。
1.1 IA-CAES数学模型
1.1.1 压缩阶段
储能阶段,第i级压缩机的出口压力为：
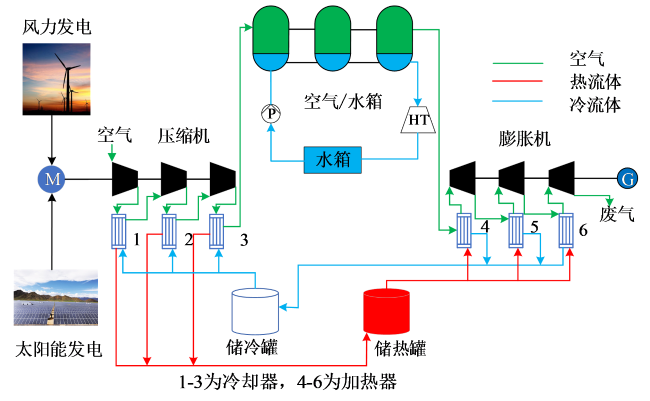
${{p}_{\text{c},\text{out},i}}={{\lambda }_{i}}{{p}_{\text{c},\text{in},i}}$ (1)
式中：pc,in,i和λi分别是第i级压缩机入口压力和压缩比。
第i级压缩机的等熵出口温度为：
${{T}_{\text{c},\text{out},i}}={{T}_{\text{c},\text{in},i}}+{{{T}_{\text{c},\text{in},i}}\left[ {{\left( {{\lambda }_{i}} \right)}^{\frac{\gamma -1}{\gamma }}}-1 \right]}/{{{\eta }_{\text{c}}}}\;$ (2)
式中：γ为绝热指数;Tc,in,i为第i级压缩机入口温度。
非设计工况下等熵效率[8]为：
${{\eta }_{\text{c}}}=\eta _{\text{c}}^{0}\left[ 1-{{a}_{4}}{{\left( 1-{{{\bar{n}}}_{\text{c}}} \right)}^{2}} \right]\left( {{{{\bar{n}}}_{\text{c}}}}/{{{{\bar{m}}}_{\text{c}}}}\; \right)\left( 2-{{{{\bar{n}}}_{\text{c}}}}/{{{{\bar{m}}}_{\text{c}}}}\; \right)$ (3)
其中$\bar{m}_{c}$与$\bar{n}_{c}$的表达式分别为：
${{\bar{m}}_{\text{c}}}=\frac{{{{m}_{\text{c}}}\sqrt{T_{\text{c},\text{in},i}^{0}}}/{{{p}_{\text{c},\text{in},i}}}\;}{{m_{\text{c}}^{0}\sqrt{T_{\text{c},\text{in},i}^{0}}}/{p_{\text{c},\text{in},i}^{0}}\;}$ (4)
${{\bar{n}}_{\text{c}}}=\frac{{{{n}_{\text{c}}}}/{\sqrt{{{T}_{\text{c},\text{in},i}}}}\;}{{n_{\text{c}}^{0}}/{\sqrt{T_{\text{c},\text{in},i}^{0}}}\;}$ (5)
式中：nc和mc分别为压缩机实际转速与实际质量流量;上标0代表设计工况条件。
压缩阶段压缩机组做功为：
${{W}_{\text{c}}}=\int_{0}^{{{t}_{\text{c}}}}{{{c}_{p,\text{a}}}\sum\limits_{i=1}^{3}{{{m}_{\text{c}}}\left( {{T}_{\text{c},\text{out},i}}-{{T}_{\text{c},\text{in},i}} \right)}}\text{d}t$ (6)
式中：cp,a为空气比热容;tc为充电时间。
换热器的有效性系数定义为[9]：
$\varepsilon =\frac{1-exp\left[ \left( -{{N}_{\text{TU}}} \right)\left( 1+{{C}_{\text{r}}} \right) \right]}{1-{{C}_{\text{r}}}\exp \left[ \left( -{{N}_{\text{TU}}} \right)\left( 1+{{C}_{\text{r}}} \right) \right]}$ (7)
其中Cr与NTU的表达式分别为：
${{C}_{\text{r}}}=\frac{{{\left( {{c}_{p,\text{a}}}{{m}_{\text{c}}},{{c}_{p,\text{w}}}{{m}_{\text{w}}} \right)}_{\min }}}{{{\left( {{c}_{p,\text{a}}}{{m}_{\text{c}}},{{c}_{p,\text{w}}}{{m}_{\text{w}}} \right)}_{\max }}}$ (8)
${{N}_{\text{TU}}}=\frac{{{U}_{\text{A}}}}{{{\left( {{c}_{p,\text{a}}}{{m}_{\text{c}}},{{c}_{p,\text{w}}}{{m}_{\text{w}}} \right)}_{\min }}}$ (9)
式中：cp,w和mw分别为工作流体的比热容和质量流量。UA为2 500 W/K[9]。
i+1级压缩机入口温度为：
${{T}_{\text{c},\text{in},i+1}}=\left( 1-\varepsilon \right){{T}_{\text{c},\text{out},i}}+\varepsilon {{T}_{\text{cold}}}$ (10)
式中：Tcold为低温储热罐的温度。
1.1.2 等压储气阶段
压缩空气储气罐中的空气质量为：
${{M}_{\text{car}}}={{M}_{\text{car}}}\left( 0 \right)+\int_{0}^{t}{\left( {{m}_{\text{c}}}-{{m}_{\text{t}}} \right)}\ \text{d}t$ (11)
式中：Mcar(0)为初始状态下储存罐中的空气质量;mt为膨胀机中空气质量流量。
储气容量的表达式为：
${{S}_{\text{ca}}}\left( t \right)=\frac{{{M}_{\text{car}}}\left( t \right)-{{M}_{\min }}}{{{M}_{\max }}-{{M}_{\min }}}$ (12)
式中：Mmax和Mmin分别为储气罐最大和最小空气质量。
1.1.3 释能阶段
释能过程膨胀机的入口温度为：
${{T}_{\text{t},\text{in},j}}=\left( 1-\varepsilon \right){{T}_{\text{t},\text{out},j-1}}+\varepsilon {{T}_{\text{hot}}}$ (13)
式中：Tt,out,j-1为第j-1级膨胀机出口温度;Thot为高温储热罐的温度。
第j级膨胀机出口压力为：
${{p}_{\text{t},\text{out},j}}=\frac{{{p}_{\text{t},\text{in},j}}}{{{\lambda }_{j}}}$ (14)
式中：λj为膨胀机的压缩比。
非设计工况下膨胀机的等熵效率为：
${{\eta }_{\text{t}}}=\eta _{\text{t}}^{0}\left[ 1-0.3{{\left( 1-{{{\bar{n}}}_{\text{t}}} \right)}^{2}} \right]\left( {{{{\bar{n}}}_{\text{t}}}}/{{{{\bar{m}}}_{\text{t}}}}\; \right)\left( 2-{{{{\bar{n}}}_{\text{t}}}}/{{{{\bar{m}}}_{\text{t}}}}\; \right)$ (15)
其中$\bar{m}_{t}$与$\bar{n}_{t}$的表达式分别为：
${{\bar{m}}_{\text{t}}}=\sqrt{1.4-0.4\frac{{{n}_{\text{t}}}}{n_{\text{t}}^{0}}}\sqrt{\frac{{{\left( {{{p}_{\text{t},\text{out},j}}}/{{{p}_{\text{t},\text{in},j}}}\; \right)}^{2}}-1}{{{\left( {p_{\text{t},\text{out},j}^{0}}/{p_{\text{t},\text{in},j}^{0}}\; \right)}^{2}}-1}}$ (16)
${{\bar{n}}_{\text{t}}}=\frac{{{{n}_{\text{t}}}}/{\sqrt{{{T}_{\text{t},\text{in},j}}}}\;}{{n_{\text{t}}^{0}}/{\sqrt{T_{\text{t},\text{in},j}^{0}}}\;}$ (17)
式中：nt为膨胀机转速。
第j级膨胀机出口温度为[8]：
${{T}_{\text{t},\text{out},j}}={{T}_{\text{t},\text{in},j}}-{{\eta }_{\text{t}}}{{T}_{\text{t},\text{in},j}}\left[ 1-{{\left( \frac{{{p}_{\text{t},\text{out},j}}}{{{p}_{\text{t},\text{in},j}}} \right)}^{\frac{\gamma -1}{\gamma }}} \right]$ (18)
膨胀阶段的输出功为：
${{W}_{\text{t}}}=\int_{0}^{{{t}_{\text{dis}}}}{{{c}_{p,\text{a}}}\sum\limits_{j=1}^{3}{{{m}_{\text{t}}}\left( {{T}_{\text{t},\text{out},j}}-{{T}_{\text{t},\text{in},j}} \right)}}\text{d}t$ (19)
式中：tdis为放电时间。
1.2 液流电池数学模型
液流电池采用恒定功率来储能和释能,其表达式为[10]：
${{S}_{\text{fb,ch}}}\left( t \right)={{S}_{\text{fb}}}\left( t-1 \right)+\left( \frac{{{\eta }_{\text{ch}}}}{{{C}_{\text{Fra}}}}\int_{0}^{{{t}_{_{\text{F1}}}}}{{{P}_{\text{Fch}}}\text{d}t} \right)$ (20)
${{S}_{\text{fb,dis}}}\left( t \right)={{S}_{\text{fb}}}\left( t-1 \right)-\left( \frac{{{\eta }_{\text{dis}}}}{{{C}_{\text{Fra}}}}\int_{0}^{{{t}_{_{\text{F2}}}}}{{{P}_{\text{Fdis}}}\text{d}t} \right)$ (21)
式中：Sfb,ch(t)和Sfb,dis(t)分别为充电和放电后t时刻的液流电池储能容量;Sfb(t-1)为t-1时刻的液流电池储能容量;PFch、PFdis、ηch、ηdis分别为液流电池的充电功率、放电功率、储能效率和释能效率;tF1、tF2分别为液流电池的储能时间和释能时间。
2 风光耦合混合储能系统优化
2.1 目标函数
以混合储能系统的最大收益为目标函数,其表达式为：
$U=\max \left[ \begin{align} & {{Y}_{\text{SE}}}+{{Y}_{\text{EP}}}-{{C}_{\text{BE}}}- \\ & \left( {{C}_{\text{IN}}}+{{C}_{\text{OM}}} \right)\times 7/{{N}_{\text{days}}} \\ \end{align} \right]$ (22)
式中：YSE为售电收益;YEP为环保收益;CIN为安装成本;CBE为购电成本;COM为维护成本;Ndays为一年系统工作天数。其中式（22）中各项参数表达式为：
$\left\{\begin{aligned} Y_{\mathrm{SE}}+ & Y_{\mathrm{EP}}-C_{\mathrm{BE}}=P_{\mathrm{yh}}(t) c_{\mathrm{gs}}(t)+P_{\mathrm{L}}(t) c_{\mathrm{gb}}(t)+ \\ & {\left[P_{\mathrm{L}}(t)-P_{\mathrm{G}}(t)\right] c_{\mathrm{En}}+P_{\mathrm{G}}(t) R_{\mathrm{s}}(t) } \\ C_{\mathrm{IV}}= & \left(\begin{array}{l} N_{\mathrm{Wt}} R_{\mathrm{Wt}}+S_{\mathrm{Pv}} R_{\mathrm{Pv}}+P_{\mathrm{Cra}} c_{\mathrm{Inv}, \mathrm{p} 1}+ \\ C_{\mathrm{Cra}} c_{\mathrm{Inv}, \mathrm{cl}}+P_{\mathrm{Fra}} c_{\mathrm{Inv}, \mathrm{p} 2}+C_{\mathrm{Fra}} c_{\mathrm{Inv}, \mathrm{c} 2} \end{array}\right) \frac{r(1+r)^{L}}{(1+r)^{L}-1} \\ C_{\mathrm{OM}}= & C_{\mathrm{Cra}} O_{\mathrm{M}, \mathrm{C}}+C_{\mathrm{Fra}} O_{\mathrm{M}, \mathrm{F}}+R_{\mathrm{Wt}} O_{\mathrm{M}, \mathrm{Wt}}+R_{\mathrm{Pv}} O_{\mathrm{M}, \mathrm{Pv}} \end{aligned}\right.$ (23)
式中：Pyh(t)、cgs(t)、PL(t)、cgb(t)、PG(t)分别为t时刻的售电功率、售电价格、负荷功率、上网电价及购电功率;cEn为环保收益[7];NWt、RWt分别为风力机数量和单位价格;SPv、RPv分别为光伏面积和单位价格;cInv,c1和cInv,p1分别为IA-CAES单位功率和容量的安装成本;cInv,c2和cInv,p2分别为液流电池单位功率和容量的安装成本;r为投资利率;L为混合储能系统寿命;OM,C、OM,F、OM,Wt、OM,Pv分别为IA-CAES、液流电池储能系统、风机和光伏系统的单位容量维护成本。
2.2 约束条件
系统的功率约束是优化容量配置的重要因素之一。该系统功率及容量约束为：
$\left\{ \begin{align} & {{P}_{\text{Wt}}}\left( t \right)+{{P}_{\text{Pv}}}\left( t \right)+{{P}_{\text{t}}}\left( t \right)+{{P}_{\text{Fdis}}}\left( t \right){{\eta }_{\text{F}}}+{{P}_{\text{G}}}= \\ & {{P}_{\text{B}}}\left( t \right)+{{P}_{\text{c}}}\left( t \right)+{{P}_{\text{Fch}}}\left( t \right)/{{\eta }_{\text{ch}}}+{{P}_{\text{du}}}(t)\text{ } \\ & 0\le {{P}_{\text{c}}}\left( t \right)+{{P}_{\text{t}}}\left( t \right)\le {{P}_{\text{Cr}}} \\ & 0\le {{P}_{\text{Fch}}}\left( t \right)+{{P}_{\text{Fdis}}}\left( t \right)\le {{P}_{\text{Fr}}} \\ & 0\le {{W}_{\text{Wt}}}+{{W}_{\text{Pv}}}+{{W}_{\text{ca}}}+{{W}_{\text{fb}}}\le 10P_{\text{B}}^{\max } \\ \end{align} \right.$ (24)
式中：Wwt、WPv、Wca、Wfb分别为风力机、光伏系统、IA-CAES和液流电池的额定容量。混合储能系统的容量约束为最大负荷的10倍[7]。
2.3 求解算法
3 运行策略及算例分析
3.1 初始条件及场景设置
Fig. 5 Typical hourly load demand curve图5 典型小时负荷需求曲线 |
Table 1 Scene setting表1 场景设置 |
| 场景 | NWt/台 | SPv/m2 | 实际功率/MW | 理论功率/MW |
|---|---|---|---|---|
| 1 | 6 | 6 411 | 6.28 | 17.88 |
| 2 | 7 | 7 479 | 7.33 | 20.87 |
| 3 | 8 | 8 547 | 8.38 | 23.85 |
| 4 | 9 | 9 616 | 9.42 | 26.83 |
| 5 | 10 | 10 684 | 10.47 | 29.91 |
表2为风电耦合混合储能系统的基本参数。IA-CAES和液流电池初始储能容量为额定储能容量的50%,且储能容量范围限制在10% ~ 90%;IA-CAES以0.5 MW∙h和0.5 MW的步长在约束范围内全局寻优。出售电价与上网电价执行2022年内蒙古自治区的电网电价。
| 参数 | 数值 | 参数 | 数值 | |
|---|---|---|---|---|
| 压缩机额定等熵效率 | 0.83 | 压缩比 | 4.79 | |
| 膨胀机额定等熵效率 | 0.80 | 膨胀比 | 4.40 | |
| 储气罐压力/MPa | 10 | 绝热指数 | 1.4 | |
| 热水罐压力MPa | 0.40 | 换热器效能 | 0.85 | |
| 环境压力/MPa | 0.10 | 常温罐水温/K | 298 | |
| 环境温度/K | 298 | 热水罐水温/K | 393 | |
| 液流电池容量安装成本 /[万元/(MW∙h)] | 83.75 | 空气比热容/[J/(kg∙K)] | 1 100 | |
| 液流电池功率安装成本 /（万元/MW） | 350 | 介质比热容/[J/(kg∙K)] | 4 200 | |
| IA-CAES功率安装成本 /（万元/MW） | 298 | 液流电池充电效率 | 0.8 | |
| IA-CAES容量安装成本 /[万元/(MW∙h)] | 59.6 | 液流电池放电效率 | 0.8 |
3.2 算例分析
不同数量的风力机和光伏系统共同作用下,风光耦合混合储能系统的经济效益情况见表3。根据求解算法得到不同场景下IA-CAES最佳容量配置,在此基础上,随着风力机和光伏系统数量的增加,系统购电量、减少弃电量及最大收益均为先增大后减少。场景1中风电场与光伏电站每小时实际输出功率仅为6.28 MW,远小于负荷需求,购电量为减少弃电量的2.77倍,使得最大收益为负;场景2中风电场与光伏电站每小时实际输出功率为7.33 MW,小于负荷需求,购电量成本增加,使得最大收益较小;场景3中风电场与光伏电站每小时实际输出功率为8.38 MW,接近负荷需求8.82 MW,在IA-CAES最佳配置下,可减少弃电量147.32 MW∙h,购电量仅为5.71 MW,最大收益为30 543.86元;场景4和场景5由于风力机与光伏系统数量过多,使系统投资及运行成本增加,但减少的弃电量急速下降,出现最大收益下滑的现象。综上,针对负荷需求的变化,确定合理的风力机与光伏系统运行数量,并配置最佳的IA-CAES容量存储规模可有效提升系统的经济效益。对于典型小时负荷为8.82 MW的工厂用户,采用8台风力机与8 547 m2光伏系统（风力机与光伏系统的装机功率分别为20 MW和3.42 MW）是可行的。下面将进一步分析IA-CAES的额定容量与功率对系统收益的影响。
Table 3 Multi-scenario maximum benefit analysis表3 多场景最大收益分析 |
| 场景 | IA-CAES最佳配置 | 减少弃电量/(MW∙h) | 购电量/(MW∙h) | U/元 | |
|---|---|---|---|---|---|
| PCra/MW | CCra/(MW∙h) | ||||
| 1 | 3.5 | 37.0 | 81.44 | 225.23 | -7 239.81 |
| 2 | 3.5 | 64.5 | 138.85 | 70.21 | 1 036.97 |
| 3 | 4.0 | 46.5 | 147.32 | 5.71 | 30 543.86 |
| 4 | 3.0 | 26.0 | 96.42 | 5.13 | 6 702.18 |
| 5 | 2.5 | 12.5 | 51.92 | 6.04 | -6 715.06 |
Fig. 6 Charge state curve of hybrid energy storage system图6 混合储能系统充电状态曲线 |
在场景3中,风光耦合混合储能系统的电力调度如图7所示,一周中购电量仅为5.71 MW∙h,弃电功率为146.49 MW∙h,弃电区间占总时长的10.71%。图中液流电池未达到最低容量且仅有5.95%时间容量低于50%,所选容量符合设计要求;压缩空气储能处于容量上限和下限的时间占总时间的百分比为15.47%,且一周循环后容量大于50%,确保了混合储能系统周期性、可重复利用的功效,验证了模型的可靠性。
Fig. 7 Power dispatching of wind-solar hybrid energy storage system图7 风光耦合混合储能系统电力调度 |
IA-CAES系统容量优化配置过程如图8所示,其中蓝色平面表示收益为0的曲面,随着额定容量与额定功率的增加,系统最大收益先增大后减小,表明在A点收益最大,此点额定容量为46.5 MW∙h、额定功率为4 MW时,可获得最大收益30 543.86元。
Fig. 8 Optimal configuration of IA-CAES system capacity图8 IA-CAES系统容量优化配置 |
4 结论
为改善风光波动性、需求负荷不确定性及IA-CAES动态响应慢等问题,建立了非工况IA-CAES系统模型,以液流电池作为改善IA-CAES 动态响应慢的问题,并采用猫群算法求解以最大收益为优化目标的最佳容量配置,算例分析表明：
（1）风力机数量会影响风光耦合系统的经济效益,风力机数量增多会增加系统弃电量,并使投资成本增加;风力机数量减少会增加大额的购电成本。综合分析结果显示选择风力机与光伏系统的装机功率分别为20 MW和3.42 MW时经济效益最佳。
（2）对于IA-CAES和液流电池配置额定功率分别为4 MW、8 MW,额定容量分别为46.5 MW∙h、1.5 MW∙h时可满足用户小时负荷8.82 MW的电力需求,每周可节约购电成本183 688.24元,周最大收益为30 543.86元。