0 引言
我国地热资源储量丰富,分布广泛。在地热资源中,干热岩地热能体现出巨大的开采价值。据统计,我国大陆3 ~ 10 km深度的干热岩所蕴含的能量折合成标准煤为856万亿吨[1,2,3],而2022年全国能源消费总量为54.1亿吨标准煤,并且国家能源局等八部门联合印发的《关于促进地热能开发利用的若干意见》[4]中提到“到2025年,地热能供暖（制冷）面积比2020年增加50%;到2035年,地热能供暖（制冷）面积及地热能发电装机容量力争比2025年翻一番”。由此可见,我国在地热资源方面具有巨大的优势与潜力,并且随着国家政策的支持,干热岩地热能有望在未来成为能源结构中的重要组成部分,为实现能源结构转型作出重要贡献。
目前干热岩地热能的开采方式主要有增强型地热系统及同轴套管换热系统,而超长重力热管（super-long gravity heat pipe, SLGHP）采热系统属于一种新型的干热岩地热能开采技术,其由蒋方明等[5]提出。随后,HUANG等[6]通过数值模拟比较了热储与热管组合系统（reservoir and heat pipe system, RHPS）和常规井下热交换器（downhole heat exchanger, DHE）系统的热提取性能,计算发现RHPS比DHE系统具有更好的热提取性能;HUANG等[7]在河北唐山进行了3 000 m重力热管取热实验,通过现场测试证实了利用SLGHP提取干热岩地热能的技术可行性,为开采深层地热能提供了一条新颖的技术路径。针对热管与热泵系统联合应用的研究,LIM等[8]通过对比带有二级回路地面热交换器地源热泵、直接膨胀式地源热泵和重力热管式地源热泵,分析其能耗和性能系数（coefficient of performance, COP）,发现了使用热管作为地热交换器的节能潜力;OCHSNER[9]开发了一种新型的CO2热管,将其与热泵系统结合进行研究;EBELING等[10]将重力热管与热泵系统结合,对重力热管的传热性能进行了实验研究,实验中重力热管长368 m,使用CO2工质,采热功率约22 kW。
目前SLGHP开采干热岩地热能已取得阶段性进展,亟需开展与之相适应的热利用方面的研究,且重力热管与热泵联合应用方面的研究所涉及的重力热管的长度都较短。基于此,本文主要针对深层地热能的热泵供热利用展开研究,将SLGHP与热泵系统结合,基于热力学第一、二定律和技术经济指标建立系统热力经济性模型,研究不同参数对系统热力经济性的影响,进一步推动干热岩地热能的开采及利用。
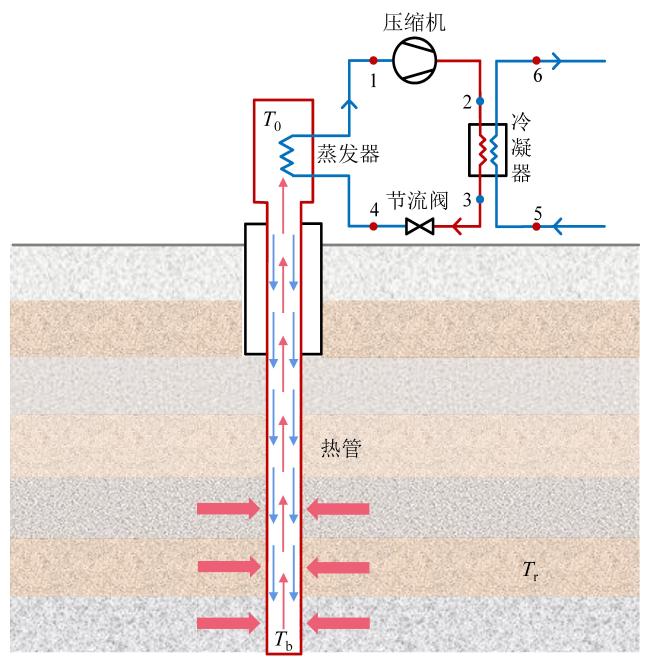
1 系统描述
Fig. 1 Schematic diagram of SLGHP combined heat pump system图1 SLGHP联合热泵系统原理图 |
SLGHP内循环工质在重力的作用下在管内发生气液相变产生自然对流效应。假定循环工质在热管两端温度分别为T0和Tb,地层中某一点的温度为Tr,循环工质从地层吸取热量后将热量迅速从热管高温端传到低温端,而热管与热泵系统之间通过蒸发器进行热量传递,热泵循环主要由四个过程组成,以制冷剂R22为例,首先R22在蒸发器内定压吸取热管传出的热量变成过热蒸汽进入压缩机（4→1过程）,其次R22在压缩机中经过绝热压缩过程变为高温高压的气体进入到冷凝器（1→2过程）,然后在冷凝器中经过定压放热过程冷凝为低温高压的液体流向节流阀（2→3过程）,最后低温高压的液体经过节流阀膨胀变为低温低压的气液两相流体（3→4过程）,随后再次进入到蒸发器进行定压吸热,如此循环工作。5→6过程为用户端从冷凝器进行换热的过程。
2 系统模型
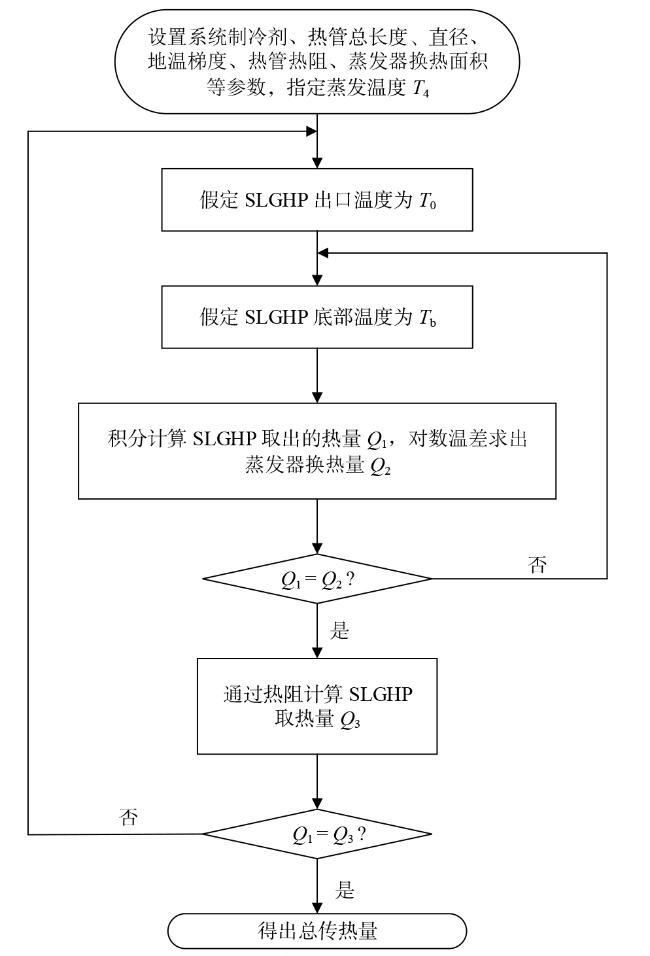
2.1 热力学模型
涉及的物性参数均由Refprop9.1提供,该系统模型的基本假设如下：
（1）换热器处的热量损失忽略不计;
（2）压缩机中为绝热压缩过程,且等熵效率为压比的函数;
（3）蒸发器出口设有一定的过热度[11];
（4）用户侧进水温度为35 ℃,出水温度为45 ℃[12];
（5）冷凝器出口工质温度为50 ℃。
参考文献[13],将恒温带温度定为12 ℃,恒温带深度定为20 m。
地温梯度ΔT的计算公式为：
$\Delta T=\frac{{{T}_{\text{c}}}-{{T}_{\text{h}}}}{{{H}_{\text{c}}}-{{H}_{\text{h}}}}$ (1)
式中：Tc为地层测温点温度,℃;Th为恒温层温度,℃;Hc为测温点深度,m;Hh为恒温层深度,m。
${{Q}_{1}}=\int\limits_{{{h}_{0}}}^{{{h}_{1}}}{\pi {{d}_{\text{w}}}U\left( {{T}_{\text{r}}}-T \right)}\text{ d}h$ (2)
式中：h为热管某一点距离地表的深度,m;h0为热管温度与地层温度相等时,距离地表的深度,m;h1为热管最底部距离地表的深度,m;dw为SLGHP的直径,取经验值,0.16 m;U为总传热系数,W/(m2∙℃);Tr为未受扰动的地层温度,℃;T为热管温度,℃。U可按照下式进行计算：
$U=\frac{0.6{{k}_{1}}}{{{d}_{\text{w}}}}$ (3)
式中：k1为热管与地层之间的典型有效导热系数,取值参考文献[14],4 W/(m∙℃)。
假定地温及热管温度均按线性变化,则未受扰动的地层温度Tr为：
$\left\{ \begin{align} & {{T}_{\text{r}}}=12\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h\le 20 \\ & {{T}_{\text{r}}}=\Delta T\left( h-20 \right)+12\ \ \ \ \ \ h>20 \\ \end{align} \right.$ (4)
SLGHP任意一点温度T为：
$T=\frac{\left( {{T}_{\text{b}}}-{{T}_{0}} \right)h}{L}+{{T}_{0}}$ (5)
式中：L为SLGHP总长度,m;Tb为SLGHP最底部循环工质温度,℃;T0为SLGHP出口端工质温度,℃。
SLGHP内部存在热阻,其对热管传热效率有很大影响。根据相关研究,SLGHP的热阻受众多因素影响,主要涉及热管几何尺寸和内部结构及工作流体种类和填充率等,可以通过优化热管结构、优选工质等方式来减小热阻,从而实现更好的气液分离效果,减小流动阻力,使得热管蒸发段温度相对均匀,提高热管传热效率。经过研究,热管性能提高以后热阻有望降低到1 × 10-5 ℃/W,甚至更低。以热阻为1 × 10-5 ℃/W展开研究,热阻R可通过下式计算：
$R=\frac{{{T}_{\text{ea}}}-{{T}_{0}}}{{{Q}_{3}}}$ (6)
式中：Tea为SLGHP蒸发段的平均温度,℃;Q3为SLGHP由蒸发段传到出口端的总热量,W。
蒸发器的入口温度为热泵系统的蒸发温度T4,为了使得制冷剂完全蒸发变为气态,设定5 ℃的过热度,则蒸发器的出口温度T1为：
${{T}_{1}}={{T}_{4}}+5$ (7)
蒸发器处换热量Q2可通过下式计算：
${{Q}_{2}}={{k}_{2}}{{A}_{\text{e}}}\frac{\left( {{T}_{0}}-{{T}_{1}} \right)-\left( {{T}_{0}}-{{T}_{4}} \right)}{\ln \left[ {\left( {{T}_{0}}-{{T}_{1}} \right)}/{\left( {{T}_{0}}-{{T}_{4}} \right)}\; \right]}$ (8)
式中：Ae为蒸发器换热面积,取值100 m2;k2为蒸发器换热系数,取经验值[15],2 500 W/(m2∙℃)。
在系统模型假设条件下,热管与地层之间的总传热量Q1、热管蒸发段到出口端的总传热量Q3与蒸发器处换热量Q2是相等的,即：
${{Q}_{1}}={{Q}_{2}}={{Q}_{3}}$ (9)
总传热量计算流程如图2 所示。
Fig. 2 Total heat transfer calculation process图2 总传热量计算流程 |
对于压缩机模型,引入等熵效率$\eta $[16],即：
$\eta =1-0.6\left[ 1-{{\left( \frac{{{P}_{2}}}{{{P}_{1}}} \right)}^{-0.3}} \right]$ (10)
式中：P1为压缩机吸气压力,Pa;P2为压缩机排气压力,Pa。
压缩机出口实际焓值${{h}_{\text{out}}}\mathrm{ }\!\!'\!\!\text{ }$可通过下式进行计算：
${{h}_{\text{out}}}\mathrm{ }\!\!'\!\!\text{ }=\frac{{{h}_{\text{out}}}-{{h}_{\text{in}}}}{\eta }+{{h}_{\text{in}}}$ (11)
式中：hin为压缩机入口焓值,J/kg;hout为压缩机出口焓值,J/kg。
对于冷凝器的面积设计,根据居民用水合理温度范围,设定用户进口端水温T5为35 ℃,出口端水温T6为45 ℃,则可以得到以下关系：
$m\left( {{h}_{\text{out}}}\mathrm{ }\!\!'\!\!\text{ }-{{h}_{\text{cout}}} \right)={{k}_{3}}{{A}_{\text{c}}}\frac{\left( {{T}_{2}}-{{T}_{6}} \right)-\left( {{T}_{3}}-{{T}_{5}} \right)}{\ln \left[ {\left( {{T}_{2}}-{{T}_{6}} \right)}/{\left( {{T}_{3}}-{{T}_{5}} \right)}\; \right]}$ (12)
式中：m为热泵系统中制冷剂的循环流量,kg/s;hcout为冷凝器出口焓值,J/kg;Ac为冷凝器换热面积,m2;T2为压缩机出口温度,℃;T3为冷凝器出口温度,℃;k3为冷凝器换热系数,通常以R22为制冷剂的套管式冷凝器的传热系数在800 ~ 1 200 W/(m2∙℃),本文k3取1 000 W/(m2∙℃)。
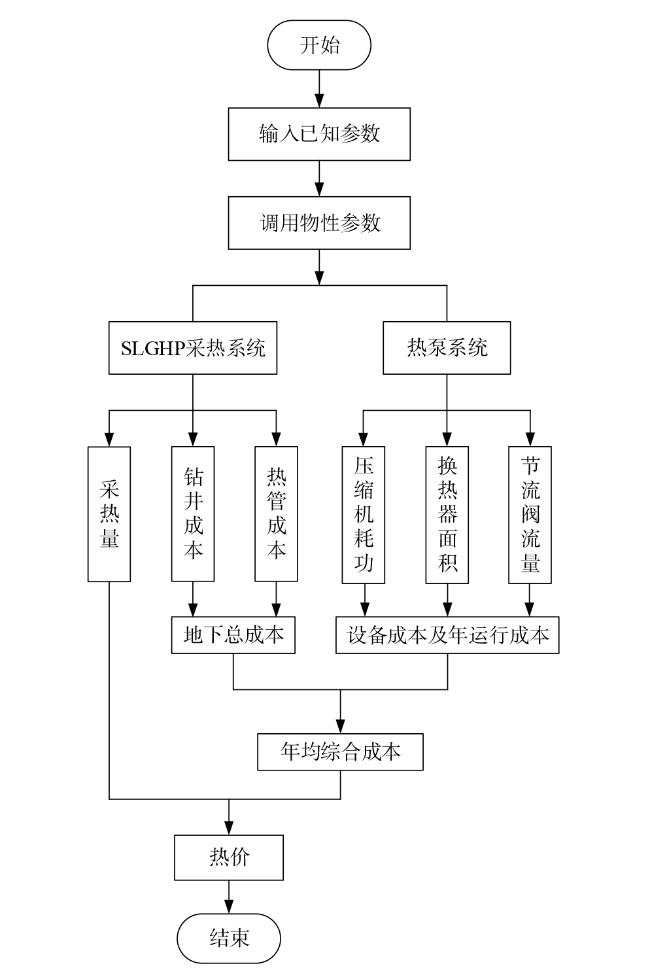
2.2 经济分析模型
对于SLGHP与热泵联合组成的系统,主要考虑初始固定资本投资、年运行成本、年均总成本和投资回收年限等技术经济指标,基于经济指标建立经济性模型,如图3 所示,该组合系统主要包括地下SLGHP采热系统和地面热泵系统。
Fig 3 Economic calculation model图3 经济性计算模型 |
对于SLGHP采热系统,主要包括钻井成本和热管成本,其中钻井所需要的费用不仅与打井深度有关,还与钻井位置等因素有关,通过拟合,可以得到一口井的钻井成本Cw约为[17]：
${{C}_{\text{w}}}={{U}_{\text{d}}}\cdot \frac{H\left( H+1000 \right)}{2000}$ (13)
式中：Ud为单位钻井成本,通过拟合可得到其为1 000元/m;H为钻井深度,m。
而SLGHP本身所需总成本Cp为：
${{C}_{\text{p}}}={{U}_{\text{p}}}\cdot L$ (14)
式中：Up为单位重力热管成本,根据热管市场价格可以确定其为600元/m。
根据调研市场组件的价格,通过函数拟合可以得到热泵系统中压缩机成本Ccomp、蒸发器（列管式换热器）成本Cevap、冷凝器（套管式换热器）成本Ccond及节流阀成本Cval,可分别按下式计算：
${{C}_{\text{comp}}}=4928.2\ln \left( {{\mathrm{W}}_{\text{comp}}} \right)-5393.2$ (15)
${{C}_{\text{evap}}}=649.41{{A}_{\text{e}}}^{0.7148}$ (16)
${{C}_{\text{cond}}}=1286.4{{A}_{\text{c}}}^{0.9933}$ (17)
${{C}_{\text{val}}}=401.92{{m}_{\text{q}}}+447.76$ (18)
式中：Wcomp为压缩机功耗,kW;mq为节流阀的质量流量,kg/s。
假设安装费、管道费等其他费用占热泵系统成本的15%,则初始固定资本投资CFCI为：
${{C}_{\text{FCI}}}={{C}_{\text{wp}}}+1.15\left( {{C}_{\text{comp}}}+{{C}_{\text{evap}}}+{{C}_{\text{cond}}}+{{C}_{\text{val}}} \right)$ (19)
式中：Cwp为钻井及重力热管成本之和,元。
假设年利率为5%,井的运行年限为50年[18],资本回收系数fCR为：
${{f}_{\text{CR}}}=\frac{i{{\left( 1+i \right)}^{n}}}{{{\left( 1+i \right)}^{n}}-1}$ (20)
式中：i为年利率;n为运行年限,年。
整个系统的运营成本包括年电力成本、维护成本及管理成本。以北京为例,根据北京2022年电费收取标准,电费为0.488 3元/(kW∙h),由《北京市供热采暖管理办法》可知,北京市供暖期为11月15日至次年3月15日,为期4个月,按照120天进行计算,则压缩机耗电费用可按下式计算：
${{C}_{\text{ele}}}=e\cdot t\cdot {{W}_{\text{comp}}}$ (21)
式中：e为电价,元/(kW∙h);t为压缩机运行时间,h。
${{C}_{\text{MC}}}=0.01\left( {{C}_{\text{comp}}}+{{C}_{\text{evap}}}+{{C}_{\text{cond}}}+{{C}_{\text{val}}} \right)$ (22)
${{C}_{\text{MG}}}=0.025{{C}_{\text{MC}}}$ (23)
结合以上可以得出年运营成本CAOC为：
${{C}_{\text{AOC}}}={{C}_{\text{ele}}}+{{C}_{\text{MC}}}+{{C}_{\text{MG}}}$ (24)
年均综合成本Ctot为：
${{C}_{\text{tot}}}={{f}_{\text{CR}}}\cdot {{C}_{\text{FCI}}}+{{C}_{\text{AOC}}}$ (25)
对于投资回收年限的计算,假设银行的年利率为i,则第y年应还银行的金额Cpay为：
${{C}_{\text{pay}}}={{C}_{\text{FCI}}}\cdot i{{\left( 1-i \right)}^{y-1}}$ (26)
投资回收年限可按下式计算：
$y=\frac{{{C}_{\text{FCI}}}+\sum\limits_{1}^{y}{{{C}_{\text{pay}}}}}{S-{{C}_{\text{AOC}}}}$ (27)
式中：y为投资回收年限,年;S为每年热量售价,元。
3 结果与讨论
本文计算涉及的参数均以所取经验值为基准,若改变某个参数,则其余参数保持不变,进而研究该参数与系统热力经济性之间的相互关系。
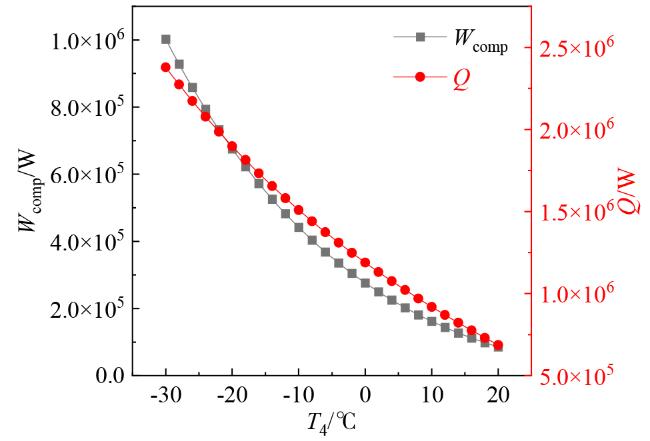
3.1 蒸发温度与成本关系
在地温梯度为30 ℃/km时,对于3 000 m深度的井,分析发现蒸发温度在一定范围变化时,单位时间内压缩机耗功及冷凝器放热量都在不断下降,如图4 所示,这主要归因于压缩机压比的降低。系统COP的变化如图5 所示,COP随蒸发温度的升高而不断增加,其原因为随着蒸发温度的升高,蒸发压力升高,压缩机压比降低,压缩功耗减小,虽然冷凝器放热量也减少,但是降幅小于压缩机功耗的减少,导致COP逐渐变大。图5 展示了供热成本的变化规律,呈现先降低后升高的趋势,在该条件下,供热成本最低时所对应的蒸发温度（即最佳蒸发温度）为 -2 ℃,这是由于随着蒸发温度降低,虽然温差逐渐增大使得系统传热量增加,但是蒸发温度降低会使得热泵系统压缩机压比增加,即压缩机功耗逐渐增加进而使年均综合成本增加,因此存在最佳蒸发温度使得供热成本最低。
Fig. 4 The relationship between compressor power consumption, condenser heat release and evaporation temperature within a unit time图4 单位时间内压缩机功耗、冷凝器放热量与蒸发温度的关系 |
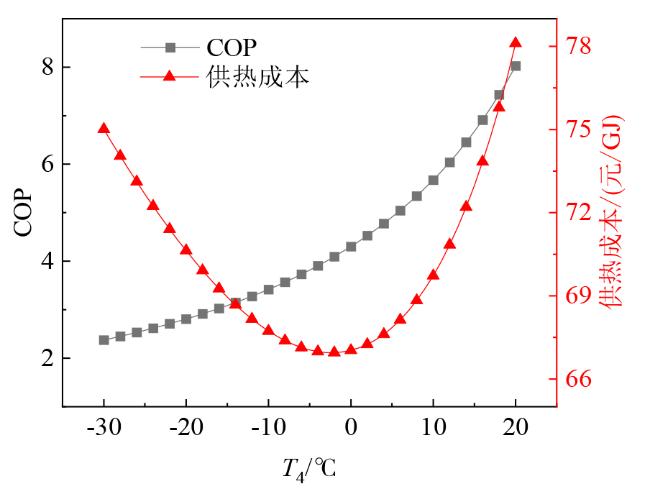
Fig. 5 The relationship between COP, heating cost and evaporation temperature图5 COP、供热成本与蒸发温度的关系 |
3.2 不同热阻与成本关系
在地温梯度为30 ℃/km时,对于3 000 m深度的井,对比研究SLGHP热阻分别为R1（1 × 10-5 ℃/W）、R2（3 × 10-5 ℃/W）及R3（5 × 10-5 ℃/W）时,蒸发温度与供热成本的关系,如图6 所示。随着蒸发温度的升高,热阻分别为R1、R2和R3时,供热成本均先降低后升高,对应的最佳蒸发温度分别为 -2、-10、-17 ℃,此时供热成本分别为66.9、76.3、84.2元/GJ。在同一蒸发温度下,热阻越小,其供热成本越低。当热阻越小时,其最佳蒸发温度越高且所对应的供热成本越小。供热成本先降低后升高主要是由于随着蒸发温度的降低会使得压缩机功耗逐渐增加,导致年均综合成本增加。在初始阶段,降低蒸发温度有助于增加传热量,但低于最佳蒸发温度后,增加的功耗会导致成本的增加超过传热量的增加,从而使得供热成本又升高。同一蒸发温度下,当热阻减小时,热管传热量增加,而打井成本及热管成本不变,因此热阻越小,供热成本越低。在换热量相同的情况下,降低蒸发温度,有助于热管传递热量,但是蒸发温度越低,压缩机功耗越大,年均综合成本越高,因此热阻越大最佳蒸发温度越低且所对应供热成本越高。
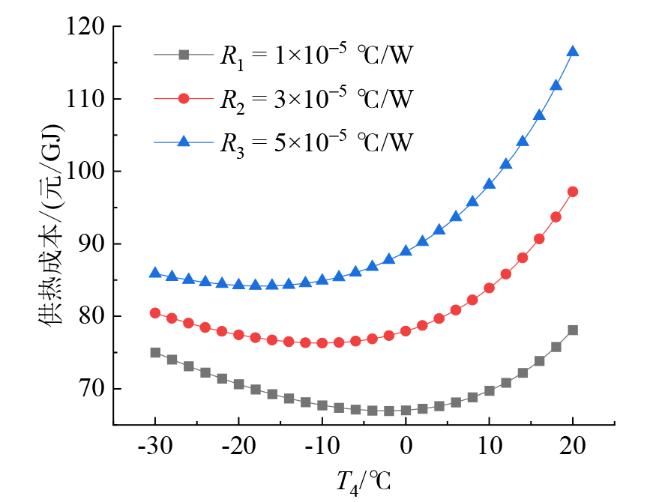
Fig. 6 The relationship between heating cost and evaporation temperature under different thermal resistances图6 不同热阻下供热成本与蒸发温度的关系 |
3.3 不同地温梯度与成本关系
在井深为3 000 m时,研究了不同地温梯度与供热成本的关系,当地温梯度从ΔT1（20 ℃/km）变化到ΔT5（60 ℃/km）时,蒸发温度与供热成本的关系如图7 所示。研究发现,地质条件越好的地方,其地温梯度越大,则供热成本相对越低。通过比较发现在同一蒸发温度下,地温梯度为60 ℃/km即地温梯度越大时,供热成本越低。当蒸发温度在 -30 ~ 20 ℃之间变化,地温梯度分别为20、30及40 ℃/km时,供热成本先降低后升高,其最佳蒸发温度分别为 -15、-2 和10 ℃,其所对应的热量成本分别为76.2、66.9和58.1元/GJ;当地温梯度为50 ℃/km和60 ℃/km时,供热成本逐渐降低,其最佳蒸发温度应高于20 ℃。综上,同一蒸发温度下,地温梯度越大,供热成本越低,这主要是由于地温梯度越大,热管采热量越多。地温梯度越大,最佳蒸发温度越高且所对应供热成本越低,这主要是因为在换热量相同的情况下,降低蒸发温度有助于热管传递热量,但是蒸发温度降低会使得压缩机功耗逐渐增加,进而使年均综合成本增加。
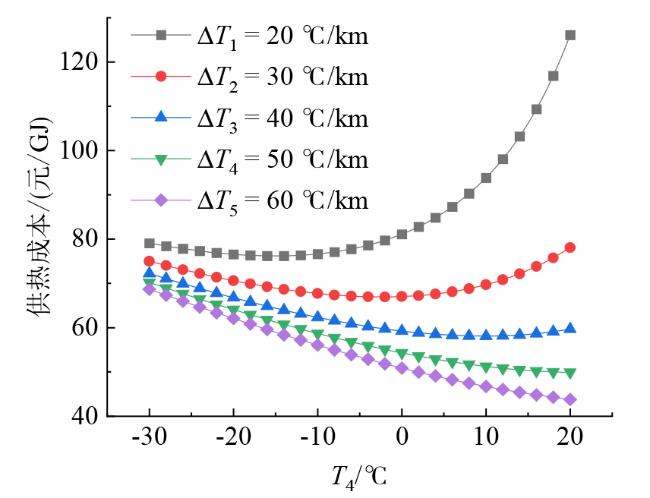
Fig. 7 The relationship between heating cost and evaporation temperature under different geothermal gradients图7 不同地温梯度下供热成本与蒸发温度的关系 |
3.4 不同井深与成本关系
在地温梯度为30 ℃/km时,研究了不同井深与供热成本的关系,当井深从H1（3 000 m）到H5（7 000 m）变化时,蒸发温度与供热成本的关系如图8 所示。研究发现,对于3 000、4 000、5 000、6 000及7 000 m深度的井,随着蒸发温度的升高,供热成本都是先降低后升高,所对应的热量成本最低分别为66.9、66.4、66.3、66.5和67.0元/GJ,其所对应的最佳蒸发温度逐渐升高,分别为 -2、3、8、12和15 ℃,即随着井深度的增加,其最佳蒸发温度逐渐升高。
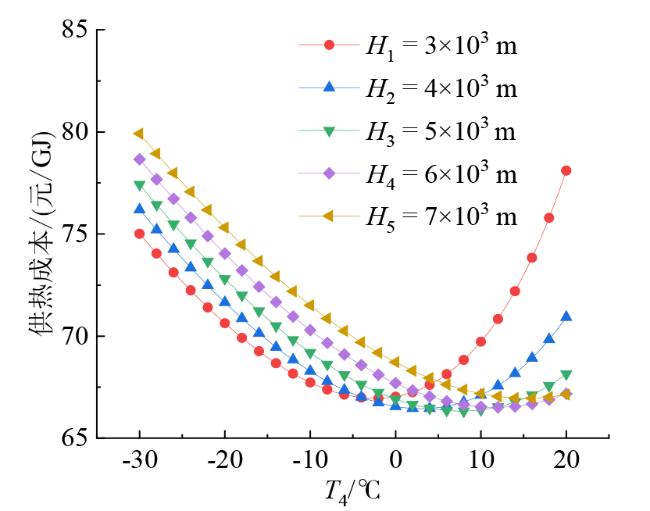
Fig. 8 The relationship between heating cost and evaporation temperature at different well depths图8 不同深度下供热成本与蒸发温度的关系 |
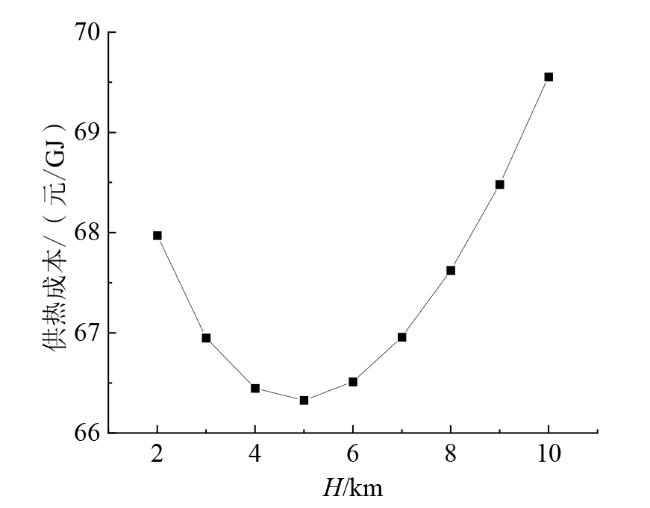
Fig. 9 The relationship between heating cost and different well depths at the optimal evaporation temperature图9 最佳蒸发温度下供热成本与不同井深的关系 |
3.5 不同蒸发器面积与成本关系
在地温梯度为30 ℃/km时,对于3 000 m深度的井,对比研究了蒸发器面积Ae分别为100、200及300 m2时,蒸发温度与供热成本的关系,如图10 所示,所对应的热量成本最低分别为66.2、65.4和65.1元/GJ。研究发现蒸发器面积一定时,随着蒸发温度的升高,供热成本关系都是先降低后升高,在同一蒸发温度下,蒸发器面积越大,供热成本越低。这主要是由于随着蒸发器面积的增加,其从地层换取的热量更多,虽然蒸发器的成本增加,但是相对来说,带来了更好的经济效益。
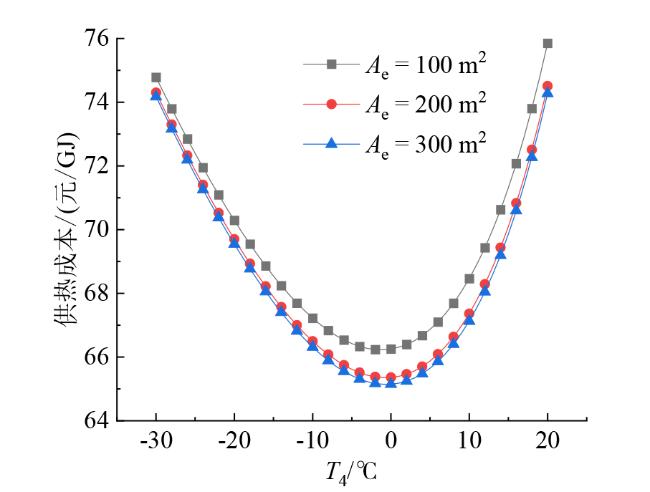
Fig. 10 The relationship between heating cost and evaporation temperature under different evaporator areas图10 不同蒸发器面积下供热成本与蒸发温度的关系 |
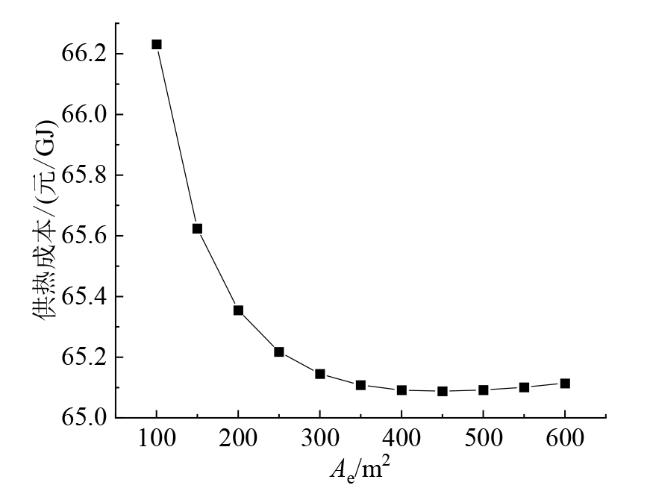
Fig. 11 The relationship between heating cost and different evaporator areas at the optimal evaporation temperature图11 最佳蒸发温度下供热成本与不同蒸发器面积的关系 |
3.6 投资回收年限分析
对于3 000 m深度的井,初始固定资本投资主要包括打井成本、热管成本及热泵机组成本,总的固定资本投资大概在800万,而每年所收取的热量费用与当地的地质条件有很大的关系,地温梯度与回收年限的关系如图12 所示,可见地温梯度越大回收年限越短,而如果有可以利用的废弃井,那么直接使用废弃井与热泵系统结合进行供热利用,可进一步缩短回收年限,因此利用SLGHP开采深层地热能并与热泵系统联合供热有很好的市场前景。
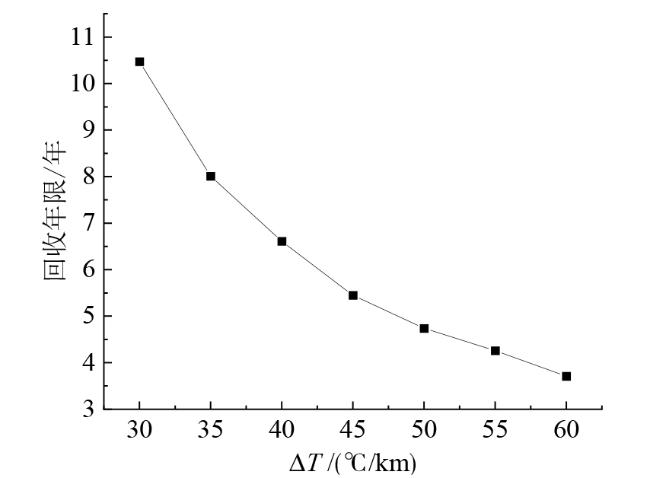
Fig. 12 The relationship between recovery period and geothermal gradient图12 回收年限与地温梯度关系 |
4 结论
将SLGHP与热泵系统结合,并对其热力经济性进行了分析,讨论了系统热力性与经济性之间的关联性,为优化SLGHP与热泵的联合系统提供理论指导,并为实际工程应用中的设计决策和操作优化提供参考,得出以下结论：
（1）COP随蒸发温度的升高不断增大,供热成本随着蒸发温度的升高先降低后升高,蒸发温度维持在特定温度时,成本最低。在地温梯度30 ℃/km、井深3 000 m的条件下,最佳蒸发温度是 -2 ℃。
（2）SLGHP热阻越小时,其经济性能越好且最佳蒸发温度越高。地温梯度越大时,其经济性能越好且最佳蒸发温度越高。
（3）当井深度一定时,随着蒸发温度的升高,供热成本先降低后升高,且随着井深度的增加,其最佳蒸发温度逐渐升高;存在一个合适的井深度使得供热成本最低。
（4）当蒸发器面积一定时,随着蒸发温度的升高,供热成本先降低后升高,在同一蒸发温度下,蒸发器面积越大,供热成本相对越低;存在一个合适的蒸发器面积使得供热成本最低。
（5）利用SLGHP与热泵系统结合进行供热,具有很好的经济效益。投资回收年限与地质条件有很大关系,如利用废弃井,则将会进一步缩短回收年限。