0 引言
扩散层主要有以下两个功能：为反应物输送至催化层提供气体通道,并将反应产生的液态水排出燃料电池[5]。扩散层是一种复杂的微孔结构,通常由碳纸或碳布制成,其内部是由多个碳纤维交错叠加而成的多孔微观结构。为了获得疏水特性和改善排水性能,通常在制备扩散层时加入一定质量分数的聚四氟乙烯（polytetrafluoroethylene, PTFE）。聚四氟乙烯侵入扩散层并附着在碳纤维表面,其中交错排列的碳纤维形成的小孔更容易被聚四氟乙烯侵占。同时,真实的聚四氟乙烯结构会占据扩散层的孔隙,降低孔隙率。扩散层的排水性能主要取决于其多孔结构和疏水特性[6]。MOLAEIMANESH等[7]通过格子玻尔兹曼方法（lattice Boltzmann method, LBM）研究了有无聚四氟乙烯的扩散层。结果表明,具有疏水特性的扩散层能极大地促进液体的排出。
然而,在燃料电池运行过程中,扩散层的结构会因老化而损坏。老化的两个原因为碳纤维的化学降解和聚四氟乙烯的机械降解。在燃料电池的运行过程中,碳纤维与液体发生反应并被氧化导致降解,也称为碳腐蚀。降解导致扩散层中的孔隙形态和表面特征发生变化,出现裂缝和大孔隙,进而改变液态水的流动行为。聚四氟乙烯降解表现为从碳纤维表面脱落,导致碳纤维疏水性能丧失,液体在亲水性碳纤维上的流动行为改变。YU等[8]通过扫描电子显微镜、X射线光电子能谱和热重分析对扩散层进行了分析。结果表明,扩散层老化会破坏碳纤维,导致扩散层的疏水性明显降低,但没有深入研究碳纤维结构的变化对排水性能的影响机理。此外,通过数值模拟研究扩散层在不同老化程度下排水性能的相关文献较少。基于以上问题,本研究采用随机算法建立聚四氟乙烯浓度梯度化设计的扩散层二维结构。同时,对扩散层进行一定程度的降解,得到扩散层降解前后的二维结构。随后,利用SHAN等[9]提出的多相伪势格子玻尔兹曼方法研究梯度化扩散层多孔结构中的气液两相流动行为。通过对扩散层进行聚四氟乙烯双梯度化设计和三梯度化设计,对比常规扩散层获得其排水性能和抗老化性能的提升,进而对不同老化程度的梯度化扩散层的排水性能进行较为准确的评价,本研究旨在通过梯度化结构提升扩散层的抗老化性能以及气体扩散能力。
1 扩散层重建方法
为了获得与激光扫描共聚焦显微镜（confocal laser scanning microscope, CLSM）和3D-X射线断层扫描观察到的相似的GDL以及微孔层（microporous layer, MPL）微观结构,依据DAINO等[10]采用的随机算法构建扩散层的二维微观结构,如图1（a、b） 所示。扩散层中的碳纤维被视为直径为7 μm、长度假定为无限长的圆柱体,是随机生成和交错的,相对于扩散层的厚度方向可被忽略。扩散层的初始孔隙率设定为65%,聚四氟乙烯的质量分数设定为10%。扩散层计算域的尺寸大小为200 μm × 100 μm,每个体素为1 μm × 1 μm,晶格域为200 × 100体素。
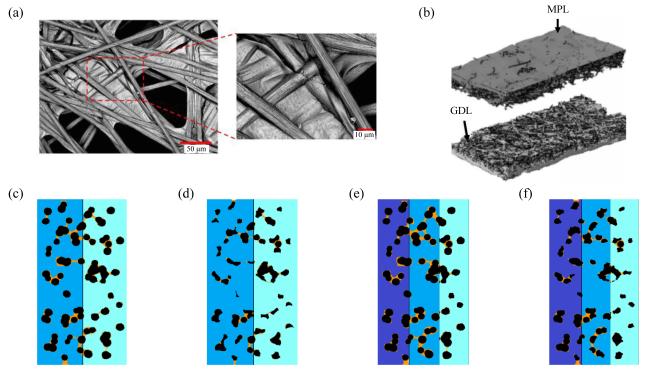
Fig. 1 GDL microstructure under CLSM (a) and 3D-X-ray tomography (b); two-dimensional microstructure of gradient diffusion layer and aging final diffusion layer (c-f)图1 CLSM（a）和3D-X射线断层扫描（b）下的GDL微观结构;梯度化扩散层及老化最终扩散层二维微观结构（c ~ f） |
采用随机算法构建了沿厚度方向呈梯度分布的聚四氟乙烯扩散层,包括双梯度化分布和三梯度化分布。双梯度化扩散层的进口（靠近催化层侧）和出口区域（靠近流场侧）,三梯度化扩散层的入口、中间和出口区域分别具有不同的聚四氟乙烯含量。随后,将常规扩散层和梯度化扩散层进行20次老化处理,为方便观察,研究了具有代表性的初始状态、老化前期状态、老化中期状态、老化后期状态、最终老化状态等5个阶段下的液态水传输行为,相应编号如表1所示。同时,假设气体扩散层中碳纤维的最终降解量为30%,聚四氟乙烯的降解量为15%[10,11]。图1（c ~ f） 显示了聚四氟乙烯总含量为10%的梯度化气体扩散层以及老化后扩散层的代表性重建微观结构。
Table 1 Design of conventional diffusion layer and gradient diffusion layer with PTFE content of 10%表1 聚四氟乙烯含量为10%的常规扩散层及梯度化扩散层设计 |
| 设计 | 方案编号 | 聚四氟乙烯分布含量/% |
|---|---|---|
| 常规扩散层 | 1 ~ 5 | 10（均匀分布） |
| 双梯度扩散层 | 6 ~ 10 | 12（进口）;8（出口） |
| 11 ~ 15 | 14（进口）;6（出口） | |
| 16 ~ 20 | 16（进口）;4（出口） | |
| 三梯度扩散层 | 21 ~ 25 | 12（进口）;10（中间）;8（出口） |
| 26 ~ 30 | 14（进口）;10（中间）;6（出口） | |
| 31 ~ 35 | 16（进口）;10（中间）;4（出口） |
2 数值模型
2.1 控制方程
$\begin{align} & {{f}_{i}}\left( x+{{e}_{i}}\Delta t,t+\Delta t \right)-{{f}_{i}}\left( x,t \right)= \\ & -\frac{1}{\tau }\left[ {{f}_{i}}^{k}\left( x,t \right)-{{f}_{i}}^{eq,k}\left( x,t \right) \right] \\ \end{align}$ (1)
式中：t为时刻;$\Delta t$为时间步长;${{e}_{i}}$为晶格速度;x为粒子位置;τ为松弛参数。平衡态分布函数${{f}_{i}}^{eq,k}\left( x,t \right)$为：
${{f}_{i}}^{eq,k}={{\omega }_{i}}{{\rho }^{k}}\left[ \begin{align} & 1+\frac{1}{{{c}_{s}}^{2}}\left( {{e}_{i}}\cdot {{u}^{eq}} \right)+\frac{1}{2{{c}_{s}}^{4}}{{\left( {{e}_{i}}\cdot {{u}^{eq}} \right)}^{2}}- \\ & \frac{1}{2{{c}_{s}}^{2}}{{\left( {{u}^{eq}} \right)}^{2}} \\ \end{align} \right]$ (2)
式中：cs为音速;ωi为权重因子;ρ为流体的宏观密度;u为宏观速度,对于D2Q9模型,${{c}_{s}}={c}/{\sqrt{3}}\;$,其中c = Δx/Δt,参考文献[13]。
为了显示流体对固体的不同润湿性,引入外力项${{F}^{k}}$。${{F}^{k}}$为组分k上的外力之和,包括表面张力F1k,流-固作用力F2k和外力F3k。
${{F}^{k}}={{F}_{1k}}+{{F}_{2k}}+{{F}_{3k}}$ (3)
流体表面张力F1k表示为：
${{F}_{1k}}\left( x \right)=-{{\psi }_{k}}\left[ {{\rho }_{k}}\left( x \right) \right]\sum\limits_{x'}{\sum\limits_{{\bar{k}}}{{{G}_{k\bar{k}}}}}\left( x,x' \right){{\psi }_{k}}\left[ {{\rho }_{k}}\left( x \right) \right]\left( x'-x \right)$ (4)
式中：${{\psi }_{k}}\left[ {{\rho }_{k}}\left( x \right) \right]$为有效密度,定义为${{\psi }_{k}}\left[ {{\rho }_{k}}\left( x \right) \right]={{\rho }_{0}}\left[ 1-\exp \left( -{{\rho }_{k}} \right){{\rho }_{0}} \right]$;${{G}_{k\bar{k}}}$为流体之间的相互作用强度,仅考虑最近的邻格粒子的作用力,其控制着两相流体的不溶性和表面张力。
流-固作用力表示为：
${{F}_{2k}}\left( x \right)=-{{\rho }_{k}}\left( x \right)\sum\limits_{x'}{{{G}_{ks}}}\left( x,x' \right){{n}_{s}}\left( x' \right)\left( x'-x \right)$ (5)
式中：ns为指示函数,ns = 1时表示固相,ns = 0时表示液相。通过调整流固相互作用强度${{G}_{ks}}$可以获得不同的接触角。
2.2 格子玻尔兹曼方法验证
2.2.1 气泡试验
表面张力是多孔介质中两相流的作用力,反映了液体分子在气液界面上的黏附力,其与多孔介质中的毛细性和润湿性密切相关。在模拟中,采用伪势多相LBM通过气泡试验来验证模型的准确性,将液体设定在气体中心,同时将所有边界设置为周期性边界,液体在计算域的中心进行动态演化,并记录液滴内外压差和液滴达到平衡时的半径。对于悬浮在气体中的液滴,应符合下述拉普拉斯定律,即液滴内外压差与表面张力成正比,与液滴半径成反比：
$\Delta P=\frac{\sigma }{R}$ (6)
式中：$\sigma $为表面张力;ΔP为液滴的内外压差;R为液滴半径。
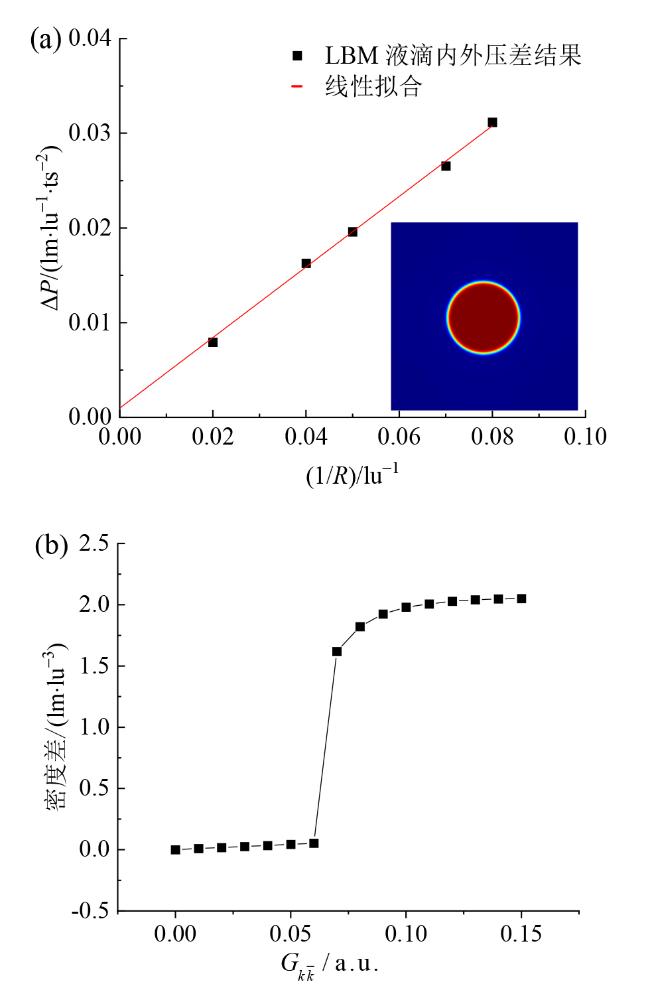
Fig. 2 Laplace's test: (a) the relationship between the pressure difference inside and outside the droplet and the reciprocal radius of the droplet; (b) the difference between the maximum and minimum density of gas with different ${{G}_{k\bar{k}}}$values图2 拉普拉斯验证：（a）液滴内外压差与液滴半径倒数之间的关系;（b）不同${{G}_{k\bar{k}}}$值的气体最大密度和最小密度之间的差异变化 |
2.2.2 静态接触角验证
接触角（θ）可以表征固体表面的润湿性。当液体在亲水性固体上时,接触角小于90°,少量液体在可湿性固体表面形成薄膜扩散。当液体处于疏水性固体中时,接触角大于90°,液体容易从非湿润固体表面脱落,通过改变Gks获得流体和固体表面之间不同的湿润性。
为了进一步验证模型的可靠性,对模型进行了静态接触角验证。设定液滴位于水平固体板上,并将计算区域的左侧和右侧设置为周期性边界条件,上部和底部设置为无滑移边界条件,观察液滴在不同Gks下的动态演化过程,记录液-固界面的接触角,如图3 所示,可以观察到通过改变Gks,接触角在逐渐变化,并且呈现近似线性关系。图3 显示的结果可用于指定不同的Gks改变固体表面的湿润特性。上述两个验证表明了本文模型的准确性。
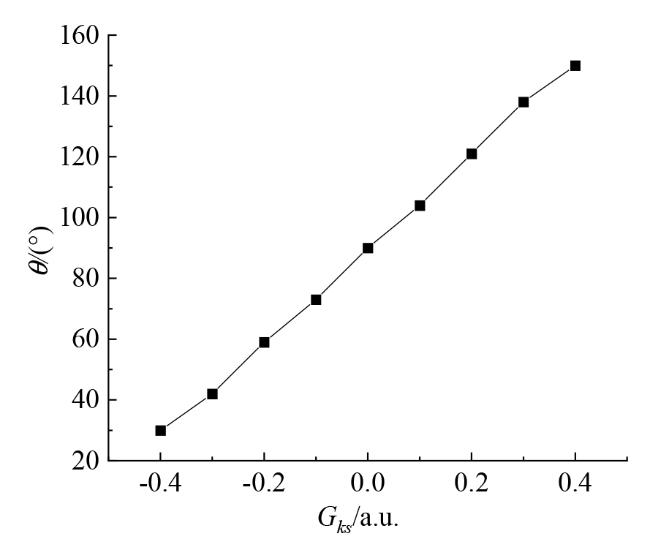
Fig. 3 Change curve of static contact angle with Gks图3 静态接触角随Gks的变化曲线 |
3 结果与分析
3.1 聚四氟乙烯双梯度的扩散层
对聚四氟乙烯含量为10%的双梯度扩散层及其5次代表性老化过程中液态水流动特性进行研究,同时与常规扩散层的相同老化过程中液态水流动特性进行了对比。图4 为常规扩散层老化过程中液态水流动过程的剖面图[14]。图5 展示了双梯度扩散层老化过程中液态水入侵过程的剖面图。可以看出无论是常规还是双梯度扩散层,液态水在扩散层内都是在毛细压力的作用下进行毛细指进运动,并倾向于入侵较大的和毛细阻力较低的孔隙,随后逐渐形成固定的流动通道,最终突破并排出扩散层。后续的液态水也会优先通过该流动通道突破。此外,随着扩散层老化程度的加剧,碳纤维和聚四氟乙烯降解导致扩散层结构破坏,造成局部毛管压力降低,进而减小了液态水入侵阻力,导致液态水饱和度含量随老化的加剧而增加,严重影响扩散层的排水性能。但相对于常规扩散层,双梯度扩散层在老化后,进口段（靠近催化层侧）仍具有较高的聚四氟乙烯含量,因此该处毛管压力依然相对较高,同时液态水突破速度依然相对较快,因此相对于同等老化程度的常规扩散层,双梯度扩散层具有较低的液态水饱和度。
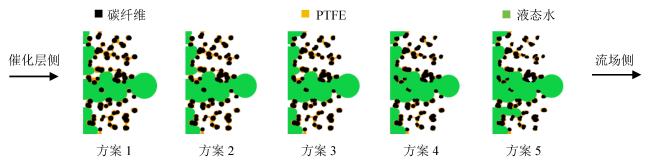
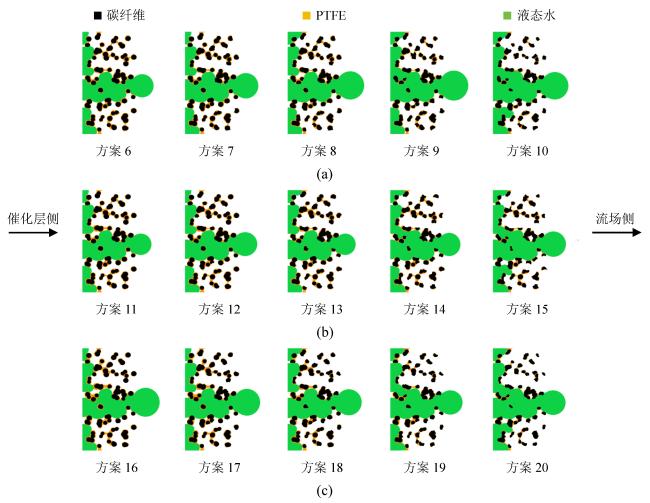
Fig. 5 Two-phase flow of polytetrafluoroethylene with double gradient distribution of diffusion layers with different aging degrees图5 聚四氟乙烯双梯度分布的扩散层不同老化程度的气液两相流形态 |
不同双梯度化扩散层在老化前后液态水饱和度和有效孔隙率变化情况如图6 所示。当双梯度扩散层靠近进口区域的聚四氟乙烯含量为14%且出口区域含量为6%时,如图5（b） 中方案11 ~ 15所示,相对于常规扩散层和其他双梯度扩散层,其在老化过程中始终具有最低的液态水饱和度含量以及最大的有效孔隙率。在最终老化状态下,其液态水饱和度为28.1%,与老化前相比,液态水饱和度增加了8.9%,而常规扩散层（图4 ）在老化后液态水饱和度增加达10.2%[14]。因此,双梯度化扩散层表现出更好的抗老化性能。
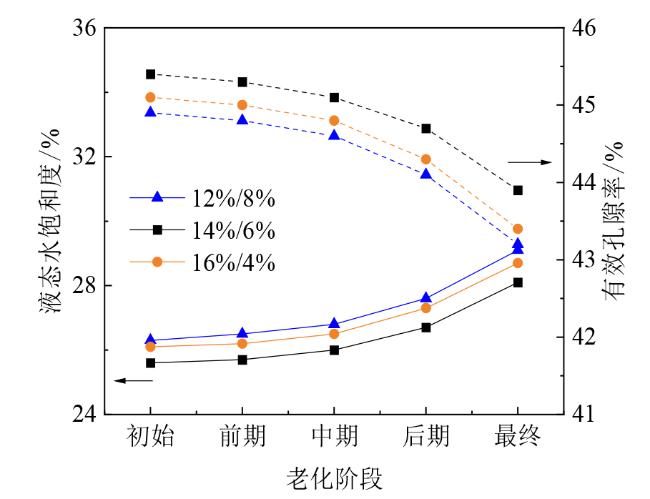
Fig. 6 Liquid saturation and effective porosity curves of double gradient diffusion layers with different aging degrees图6 双梯度扩散层不同老化程度下液态水饱和度和有效孔隙度曲线 |
3.2 聚四氟乙烯三梯度的扩散层
对三梯度扩散层的抗老化性能开展研究,如图7 所示,发现同常规扩散层和双梯度扩散一样,随着老化的加剧,碳纤维和聚四氟乙烯降解导致扩散层结构破坏,造成局部毛管压力降低,进而减小了液态水入侵阻力,液态水入侵区域增多,导致液态水饱和度含量随老化的加剧而增加,严重影响扩散层的排水性能。进一步对比图7（a） 和图7（c） 发现当扩散层进口区域分布较多的聚四氟乙烯时,在最终老化状态下,进口区域液态水突破路径较少,改善了液态水的滞留情况,同时相较于双梯度而言,聚四氟乙烯三梯度分布拥有更平缓的毛管压力分布,更有利于液态水的排出。
Fig. 7 Two-phase flow of polytetrafluoroethylene diffusion layers with different aging degrees in three gradient distribution图7 聚四氟乙烯三梯度分布的扩散层不同老化程度的气液两相流形态 |
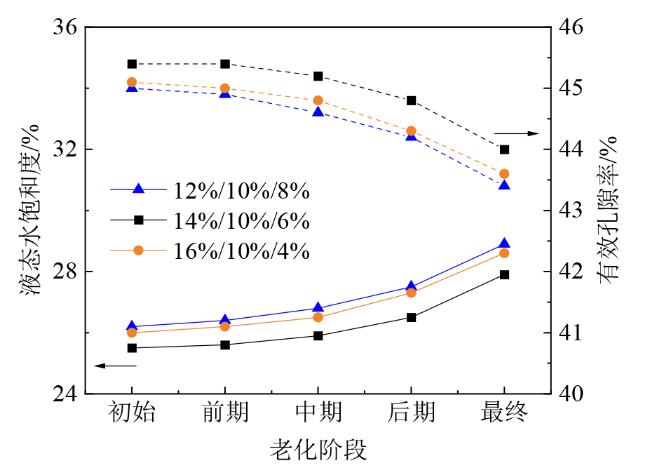
Fig. 8 Liquid saturation and effective porosity curves of three gradient diffusion layers with different aging degrees图8 三梯度扩散层不同老化程度下的液态水饱和度和有效孔隙度曲线 |
4 结论
采用随机算法重建了聚四氟乙烯总含量为10%的梯度化气体扩散层的多孔结构,其结构与扫描电镜下观察到的结构一致。随后,利用多相伪势格子玻尔兹曼方法研究了梯度化扩散层在老化过程中液态水的输运特性。模拟结果表明,扩散层的老化对液态水的传输行为有很大影响。梯度化设计的扩散层在进口区域分布较高的聚四氟乙烯能有效提供较高的毛管压力,从而减少液态水突破路径,进而提高突破速度。因此,梯度化扩散层具有较好的排水性能和气体扩散层能力。虽然老化后的扩散层因结构破坏导致毛管压力的降低,致使液态水占据更多孔隙而堵塞气体通道,但梯度化扩散层排水性能下降幅度相较于传统常规聚四氟乙烯分布的扩散层老化更低,表现出更高的抗老化性能。