0 引言
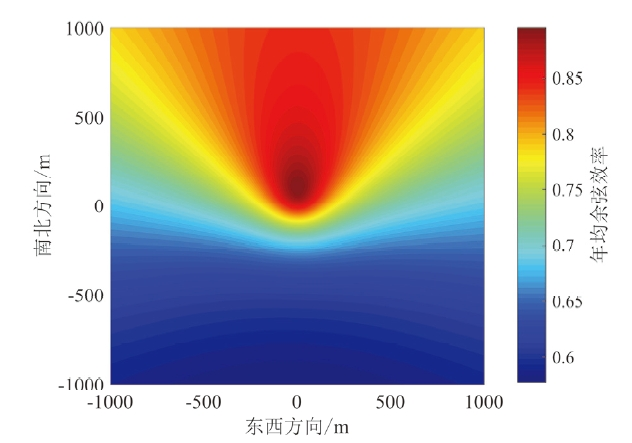
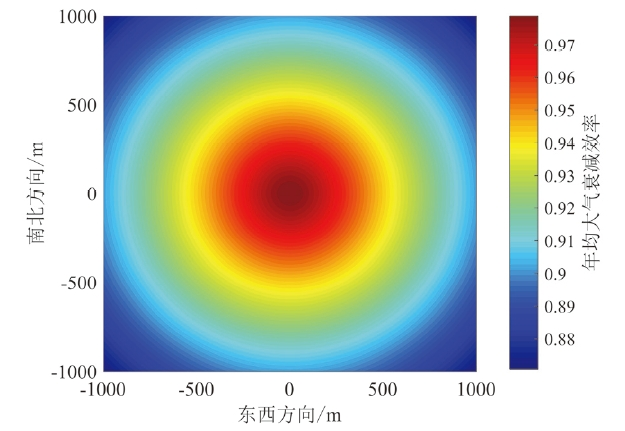
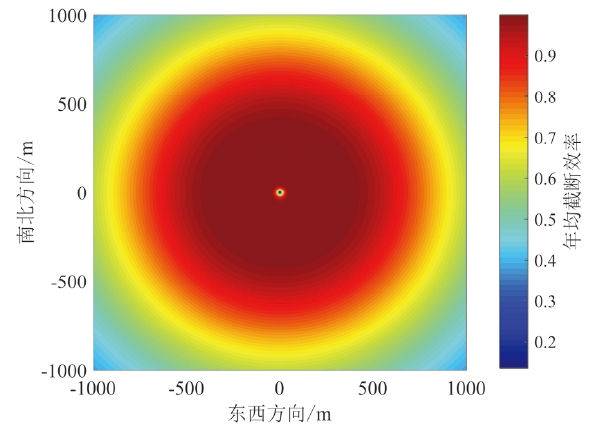
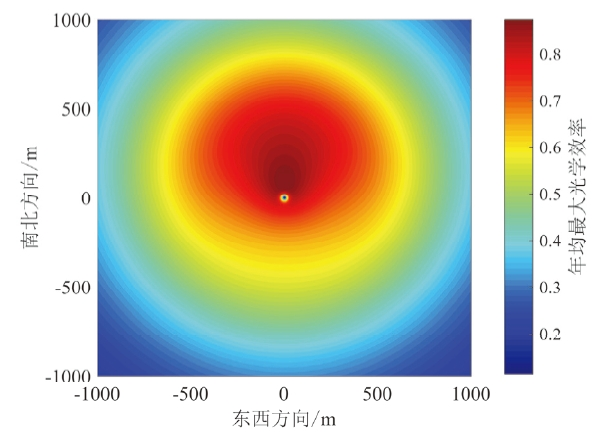
张宏丽等[5]计算了春分日12时刻定日镜场的余弦效率、大气透过效率以及腔式吸热器开口平面上的截断效率,将这三项的乘积定义为地面利用效率用于限制定日镜场的布置范围,但春分日12时刻的镜场效率存在一定的局限性,无法真实反映镜场全年光学效率的分布情况。房淼森等[6]对定日镜的能量传输效率进行了建模,对不同纬度地区全年镜场能量传输效率进行计算,并通过设定传输效率阈值确定日镜场的边界,但其60 min的采样时间间隔及20 m的采样距离精度可能产生一定误差从而影响定日镜场高效布局。高博等[7]采用自适应引力搜索算法对定日镜场进行优化布置,优化后的定日镜场的年均效率值为60.49%,镜场年均效率提升3.62%。BESARATI等[8]采用遗传算法（genetic algorithm, GA）对美国加利福尼亚州一座发电功率为50 MW的塔式太阳能定日镜场进行优化,使用594个定日镜获得了68.30%的年日照加权效率。LI等[9]采用粒子群优化（particle swarm optimization, PSO）与遗传算法相结合的混合算法（PSO-GA）对拉萨塔式太阳能3 450个定日镜进行优化,年效率从50.74%提高至56.48%,提高了约5.7%。
本文设定4 m的采样距离精度,采用日平均年光学效率的计算方法,通过对瞬时光学效率进行定积分求均值的方法代替时间离散采样,分别对定日镜年均余弦效率、大气衰减效率、截断效率及最大光学效率进行计算分析,为后续定日镜场的布置及优化提供评价指标。以西班牙Gemasolar塔式电站为例,采用密集campo布置的镜场作为初始镜场,分别验证本文计算的光学效率及布置方法的可靠性。采用差分进化算法及遗传算法对镜场进行优化,搜寻定日镜之间最佳的方位角间距和径向间距,以获得更好的镜场平均光学效率。
1 光学效率
定日镜在将太阳光反射至吸热器过程中存在许多光学效率损失,主要有大气衰减效率$\eta_{\mathrm{atm}}$、余弦效率$\eta_{\cos }$、阴影及遮挡效率$\eta_{\mathrm{sb}}$、溢出效率$\eta_{\text {int }}$ [10]。将这4项及定日镜实际反射率$\rho$的乘积定义为综合效率$\eta$,以此来指导定日镜场布局。定日镜应布置于综合效率较高的区域内,以获取更好的辐射反射效率。
$\eta=\rho \eta_{\mathrm{atm}} \eta_{\mathrm{cos}} \eta_{\mathrm{int}} \eta_{\mathrm{sb}}$ (1)
1.1 余弦效率
余弦效率损失是镜场光学效率损失最为严重的一项,极大地影响着定日镜场的布局。在定日镜反射过程中,太阳入射光线与定日镜镜面法线之间存在一个夹角θ,称为余弦角,该角的余弦值为余弦效率[11]。夹角越小,余弦效率越高。
余弦角θ可通过下式进行计算：
$\theta=\frac{1}{2} \arccos (\vec{s} \cdot \vec{q})$ (2)
式中：$\vec{S}$为定日镜中心点指向太阳方向的单位向量,$\vec{q}$为定日镜中心指向吸热器方向的单位向量。
余弦效率$\eta_{\cos }$的大小可表示为：
$\eta_{\cos }=\cos \theta$ (3)
1.2 大气衰减效率
由于大气中灰尘、二氧化碳、水分子等原因,定日镜反射的太阳辐射在由镜面到达吸热器的过程中会产生一定程度的衰减。大气衰减效率通常与定日镜和吸热器之间的距离d有关,定日镜距吸热器越近,衰减效率越高。大气衰减效率$\eta_{\mathrm{atm}}$计算公式为[12]：
$\eta_{\mathrm{atm}}=\left\{\begin{array}{l} 0.99321-0.0001176 d+1.97 \times 10^{-8} d^{2}, d \leq 1 \mathrm{~km} \\ \mathrm{e}^{-0.0001106 d}, d>1 \mathrm{~km} \end{array}\right.$ (4)
1.3 截断效率
因光散效应、定日镜追踪误差及镜面面型误差,有部分反射光线无法到达吸热器表面,反射光线被吸热器截断,由此引起定日镜的截断损失。定日镜反射至吸热器上的光斑能流密度分布接近高斯分布,截断效率$\eta_{\text {int }}$可以通过下式计算[13]：
$\eta_{\text {int }}=\frac{1}{2 \pi \sigma_{\text {tot }}^{2}} \iint_{x y} \exp \left(-\frac{x^{2}+y^{2}}{2 \sigma_{\text {tot }}^{2}}\right) \mathrm{d} x \mathrm{~d} y$ (5)
式中：积分范围为垂直于反射光线的吸热器平面的投影面;$\sigma_{\text {tot }}$为总标准误差,由下式计算得到：
$\sigma_{\text {tot }}=\sqrt{d^{2}\left(\sigma_{\text {sun }}^{2}+\sigma_{\mathrm{bq}}^{2}+\sigma_{\text {ast }}^{2}+\sigma_{\text {track }}^{2}\right)}$ (6)
式中：$\sigma_{\text {sun }}, \sigma_{\mathrm{bq}}, \sigma_{\text {ast }}$和$\sigma_{\text {track }}$分别为太阳发散角误差、镜面面型误差、像散效应误差和定日镜跟踪误差,mrad。其中,$\sigma_{\mathrm{bq}}$和$\sigma_{\text {ast }}$由下式计算[14]：
$\sigma_{\mathrm{bq}}=2 \sigma_{\mathrm{s}}$ (7)
$\sigma_{\mathrm{ast}}=\frac{\sqrt{0.5\left(H_{\mathrm{t}}^{2}+W_{\mathrm{s}}^{2}\right)}}{4 d}$ (8)
$H_{\mathrm{t}}=\sqrt{W_{\mathrm{h}} \times H_{\mathrm{h}}}\left|\frac{d}{f}-\cos \omega\right| .$ (9)
$W_{\mathrm{s}}=\sqrt{W_{\mathrm{h}} \times H_{\mathrm{h}}}\left|\frac{d}{f} \cos \omega-1\right|$ (10)
式中：$\sigma_{\mathrm{s}}$为镜面坡度引起的标准误差;$H_{\mathrm{t}}$和$W_{\mathrm{s}}$分别为反射光束所成的像在子午面和弧矢面的尺寸;$W_{\mathrm{h}}$和$H_{\mathrm{h}}$分别为定日镜宽度和高度;ω为太阳光线入射角;f为定日镜焦距,等于定日镜中心与吸热器之间的距离d。
1.4 日平均年光学效率
上文介绍了定日镜场瞬时余弦效率、大气衰减效率、截断效率及综合效率的计算方法,其计算结果存在局限性,无法真实反映镜场全年光学效率的分布情况。因此,需要对定日镜场全年的光学效率进行计算分析。
对一天的瞬时光学效率进行积分求均值来获取日均光学效率,再对365天的日均光学效率进行算术平均获取日平均年光学效率,计算公式如下[15]：
$\eta_{\text {annual }}=\frac{\sum_{\text {day }=1}^{365} \int_{t_{1}}^{t_{2}} \eta_{\text {ins }}(t) \mathrm{d} t}{\sum_{\text {day }=1}^{365} \int_{t_{1}}^{t_{2}} \mathrm{~d} t}$ (11)
式中：$\eta_{\text {annual }}$为日平均年光学效率;$t_{1}, t_{2}$分别为日出和日落时刻,通过太阳高度角进行判断;$\eta_{\text {ins }}(t)$为瞬时光学效率。
1.5 镜场性能评价指标
镜场光学效率是衡量塔式电站能量收集性能的重要指标。基于光学效率及定日镜数量可以求得镜场平均光学效率,以此作为塔式太阳能定日镜场性能的评价指标,对镜场光学效率进行定量分析[16]。
$\eta_{\text {field }}=\frac{\sum_{n=1}^{N} A_{\mathrm{h}} I_{\mathrm{b}} \eta_{n}}{N A_{\mathrm{h}} I_{\mathrm{b}}}=\frac{1}{N} \sum_{n=1}^{N} \eta_{n}$ (12)
式中：$\eta_{\text {field }}$为镜场平均光学效率;$A_{\mathrm{h}}$为定日镜反射面积;$I_{\mathrm{b}}$为太阳法向直接辐射;N为定日镜数量;$\eta_{n}$为第n个定日镜的瞬时光学效率。
2 Campo布置
Fig. 1 Densest campo layout图1 密集campo布置 |
2.1 特征直径
定日镜的特征直径等于其对角线长度加上额外安全距离,也是相邻定日镜中心之间的距离,计算公式如下：
$D_{\mathrm{M}}=D_{\mathrm{h}}+d_{\text {sep }}$ (13)
式中：$D_{\mathrm{M}}$为定日镜特征直径;$D_{\mathrm{h}}$为定日镜对角线长度;$d_{\mathrm{sep}}$为额外安全距离。
2.2 方位角间距
方位角间距是每个区域中同一环相邻定日镜之间的角距离,镜场中同一区域定日镜的方位角间距相同,计算公式如下：
$\Delta a_{z 1}=2 \arcsin \left(\frac{D_{\mathrm{M}}}{2 R_{1}}\right) \cong \frac{D_{\mathrm{M}}}{R_{1}}$ (14)
式中：$\Delta a_{z 1}$为镜场第一区域中定日镜的方位角间距,$R_{1}$为第一区域中第一环的半径。
在布置过程中,同一环相邻定日镜之间的距离随着环数的增加而增加。当相邻定日镜之间的距离变得足够大,可以在该距离中放置额外的定日镜时,需要重新定义方位角间距,从而形成新的区域。因此,第二、第三区域方位角计算公式如下：
$\Delta a_{z 2}=\Delta a_{z 1} / 2$ (15)
$\Delta a_{z 3}=\Delta a_{z 2} / 2$ (16)
式中：$\Delta a_{z 2}, \Delta a_{z 3}$分别为镜场第二、第三区域中定日镜的方位角间距。
2.3 径向间距
相邻环定日镜之间的最小径向间距等于等边三角形的高度,计算公式如下：
$\Delta R_{\min }=D_{\mathrm{M}} \cos 30^{\circ}-h \approx D_{\mathrm{M}} \cos 30^{\circ}$ (17)
式中：$\Delta R_{\min }$为相邻环定日镜之间的最小径向间距;h为相邻定日镜沿圆弧布置产生的误差距离,可忽略不计。
2.4 定日镜数量
由于相同区域定日镜的方位角间距相同,因此第一区域每一环的定日镜数量也相等,计算公式如下：
$N_{\text {hel1 }}=2 \pi / \Delta a_{z 1}=2 \pi R_{1} / D_{\mathrm{M}}$ (18)
式中：$N_{\text {hel1 }}$为第一区域中每一环定日镜的数量。
同理,对于第二、第三区域中每环定日镜数量计算公式如下：
$N_{\mathrm{hel} 2}=4 \pi R_{1} / D_{\mathrm{M}}$ (19)
$N_{\text {hel3 }}=8 \pi R_{1} / D_{\mathrm{M}}$ (20)
式中：$N_{\mathrm{he} 22}, N_{\mathrm{hel} 3}$分别为第二、第三区域中每一环定日镜的数量。
2.5 定日镜环数
由于相同区域定日镜的径向间距相同,因此第一区域的定日镜环数计算公式如下：
$N_{\text {rows1 }}=\left(R_{2}-R_{1}\right) / \Delta R_{\min }=R_{1} / \Delta R_{\min } \approx \operatorname{round}\left(R_{1} / \Delta R_{\min }\right)$(21)
式中：$N_{\text {rows1 }}$为第一区域中定日镜的环数;$R_{2}$为第二区域中第一环的半径。
同理,第二、第三区域中定日镜环数计算公式如下：
$N_{\text {rows } 2} \approx \operatorname{round}\left(2 R_{1} / \Delta R_{\min }\right)$ (22)
$N_{\text {rows } 3} \approx \operatorname{round}\left(4 R_{1} / \Delta R_{\min }\right)$ (23)
式中：$N_{\text {row } 2} \backslash N_{\text {rows3 }}$分别为第二、第三区域中定日镜的环数。
3 差分进化
差分进化算法是一种基于群体的自适应全局优化算法,其特点是简单、鲁棒、控制变量少和快速收敛,也适用于非线性和不可微的优化问题。
该算法的基本思想是：从一个随机产生的初始种群开始,通过把种群中任意两个个体的向量差与第三个个体求和来产生新个体,然后将新个体与当代种群中相应的个体相比较,如果新个体的适应度优于当前个体的适应度,则在下一代中就用新个体取代旧个体,否则仍保存旧个体。通过不断地进化,保留优良个体,淘汰劣质个体,引导搜索向最优解逼近。
3.1 种群初始化
首先,在解空间中随机均匀产生M个个体,每个个体由k维向量组成。第i个个体的j维数值$X_{i, j}$计算公式如下：
$X_{i, j}=X_{j, \min }+\operatorname{rand}(0,1)\left(X_{j, \max }-X_{j, \min }\right)$ (24)
式中：$i=1,2, \cdots, M ; \quad j=1,2, \cdots, k$。
3.2 变异
对于第G代种群中的个体$X_{i}^{G}$,使用以下公式生成变异个体$V_{i}^{G}$：
$V_{i}^{G}=X_{i}^{G}+F\left(X_{\text {best }}^{G}-X_{i}^{G}\right)+F\left(X_{r 1}^{G}-X_{r 2}^{G}\right) .$ (25)
式中：$X_{r 1}^{G}$和$ X_{r 2}^{G}$为随机选择的不同个体;F为缩放因子,取值范围一般为 [0, 2];$X_{\text {best }}^{G}$为G代中具有最佳适应度的最佳个体向量。
3.3 交叉
应用交叉运算来进一步扰动生成的解并增强分集。生成 [0, 1] 范围内的随机数,并将其与交叉因子$C_{\mathrm{r}}$进行比较,若其值大于或等于$C_{\mathrm{r}}$,则试验个体$U_{i}^{G}$取自父向量$X_{i}^{G}$,否则取变异个体$V_{i}^{G}$。
3.4 选择
分别对试验个体$U_{i}^{G}$和$X_{i}^{G}$的目标函数进行比较,若$U_{i}^{G}$具有更好的适应度,则产生的新个体$X_{i}^{G+1}=\bar{U}_{i}^{G}$;否则,新个体等于$X_{i}^{G}$。
4 结果与讨论
4.1 余弦效率
Fig. 2 Annual average cosine efficiency图2 年均余弦效率 |
将式（12）中的N设置为采样点数2.5 × 105,求得集热塔四周2 000 m × 2 000 m范围内的平均光学效率,以此对光学效率图进行定量分析。求得该区域年均余弦效率为71.24%。
4.2 大气衰减效率
图3为年均大气衰减效率图。图中可见,大气衰减效率在集热塔附近效率最高,其分布关于集热塔坐标中心对称。大气衰减效率主要取决于定日镜中心点与吸热器中心点之间的距离,定日镜离集热塔距离越远,反射光线的能量损失越大。可以看出,定日镜应尽量布置在集热塔周围较近位置处,且镜场规模不宜过大。该区域年均大气衰减效率为92.13%。
Fig. 3 Annual average atmospheric attenuation efficiency图3 年均大气衰减效率 |
4.3 截断效率
图4是年均截断效率图,与大气衰减效率类似,关于原点对称,距集热塔较近和较远位置的截断效率都较低。距集热塔较近的定日镜由于其仰角过大,导致吸热器实际采光面积减小,造成较大光学损失。根据截断效率图,定日镜应从距集热塔一定距离的位置开始布置,且镜场的规模不易过大。该区域年均截断效率为76.56%。
Fig. 4 Annual average interception efficiency图4 年均截断效率 |
4.4 最大光学效率
定日镜场年均最大光学效率如图5所示。可以看出,最大光学效率的高效率区域为偏心圆,主要分布在集热塔北部,受余弦效率的影响较大。其次,受截断效率的影响,应避免在距集热塔极近的位置处布置定日镜。该区域年均最大光学效率为50.86%。
Fig. 5 Annual average maximum optical efficiency图5 年均最大光学效率 |
4.5 镜场布置
Fig. 6 Dense campo arranged heliostat field图6 密集campo布置的定日镜场 |
4.6 镜场优化
采用差分进化算法对初始镜场进行优化,优化后的定日镜场如图7所示。通过增加定日镜之间的方位角间距和径向间距,提高定日镜场的年均综合效率。其中,阴影与遮挡效率得到了较大的提高,但也造成了其他光学效率一定程度的降低。
Fig. 7 Optimized heliostat field图7 优化后的定日镜场 |
优化前后定日镜场的年均综合效率数据见表2。镜场年均综合效率由56.99%提高到59.03%,提升了3.58%。年均综合效率的最大值有较大的提升,其最小值有一定程度的降低。
Table 2 Annual average comprehensive efficiency of heliostat field before and after optimization表2 优化前后定日镜场年均综合效率 |
| 镜场 | 年均综合效率/% | |||
|---|---|---|---|---|
| 平均数 | 中位数 | 最大值 | 最小值 | |
| 初始镜场 | 56.99 | 56.76 | 73.72 | 40.45 |
| 优化镜场 | 59.03 | 58.74 | 80.44 | 37.11 |
采用遗传算法对定日镜场进行优化,与差分进化算法优化的镜场和初始镜场进行对比,结果如图8所示。可以看出,使用遗传算法和差分进化算法对镜场优化后,镜场低效率区域的综合效率有所降低,但其中高效率区域的综合效率得到了较大的提升。使用遗传算法对镜场优化后,镜场的年均综合效率为57.94%,低于差分进化优化后的59.03%,验证了在该领域差分进化算法的优越性。
Fig. 8 Average annual comprehensive efficiency of heliostats before and after optimization图8 优化前后定日镜的年均综合效率 |
5 结论
采用日平均年光学效率的方法计算分析了定日镜的年均余弦效率、大气衰减效率、截断效率及最大光学效率。以西班牙Gemasolar塔式电站为例,采用密集campo布置的镜场作为初始镜场进行仿真及验证。采用差分进化、遗传算法对定日镜场进行优化。研究结果如下：
（1）余弦效率较高的区域为集热塔北面;距集热塔越近,大气衰减效率越高;截断效率与大气衰减效率类似,但在距集热塔极近的位置,截断效率极低;最大光学效率受余弦效率影响最大,高效率区域主要集中在集热塔北面,呈偏心圆状。
（2）以西班牙Gemasolar塔式电站为例,以密集campo布置法生成初始镜场,镜场环数为42环,共4 410个定日镜,镜场年均光学效率为56.99%,验证了本文计算的光学效率及布置方法的可靠性。
（3）采用差分进化算法对初始镜场进行优化。优化后,镜场年均综合效率为59.03%,提升了3.58%。与遗传算法的优化结果进行对比,验证了在该领域差分进化算法的有效性及优越性,可为塔式太阳能定日镜场布置及优化提供参考。