0 引言
然而，受限于相变材料的低热传导能力（液态金属除外），大部分潜热储热器面临着传热效率低下、热应力集中以及储放热过程时间过长等问题。为此，目前已经发展出增大传热面积[4⇓-6]、添加高导热增强剂[7-8]、相变材料胶囊[9]以及组合相变材料[10-11]等强化传热方法。其中，最典型的是通过添加翅片来提升潜热储热器的储放热速率。近年来相继发展出一些具有高比表面的异构翅片[12-13]和具有高效热输运特性的仿生翅片[14-15]。通过对纯相变材料的改性来提升潜热储热器性能也是最常见的手段。常见的高导热增强剂包括泡沫金属[16]、纳米颗粒[17]、碳基材质[8]以及其他高导热材质[18]。此外，将相变材料胶囊化以提升其对流换热性能的方法同样得到了快速发展。除了宏观尺度的相变胶囊[19]，得益于先进技术的微纳相变材料胶囊[20]的比表面更大且可靠性更佳。考虑到换热流体传热过程中的热滞后效应，利用组合相变材料进行热量的梯级利用可实现传热效率的最大化，进而提升潜热储热器的储放热速率[21]。
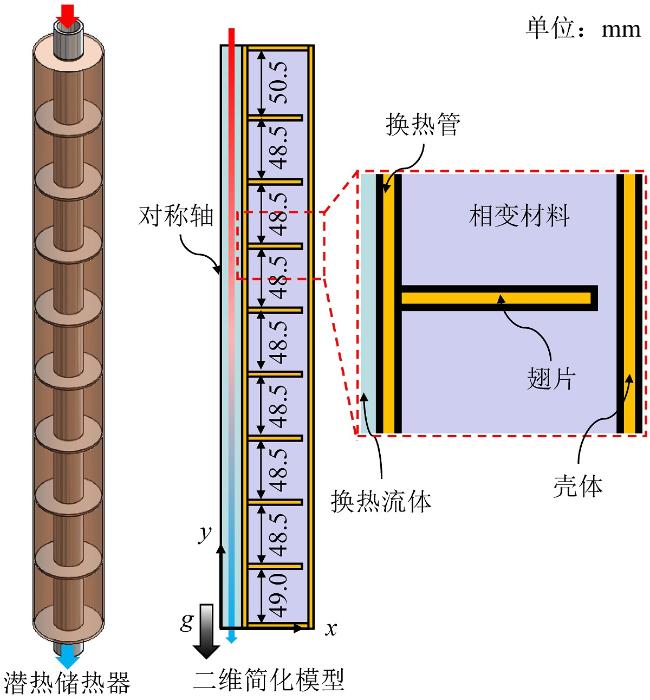
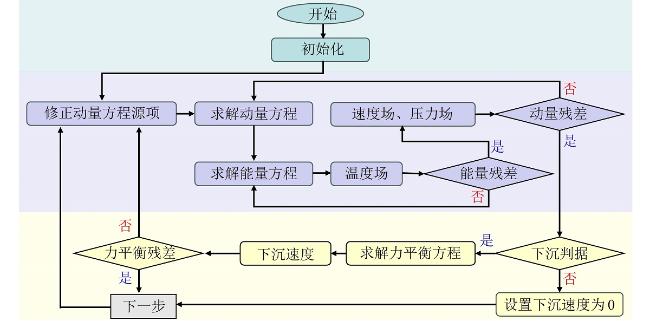
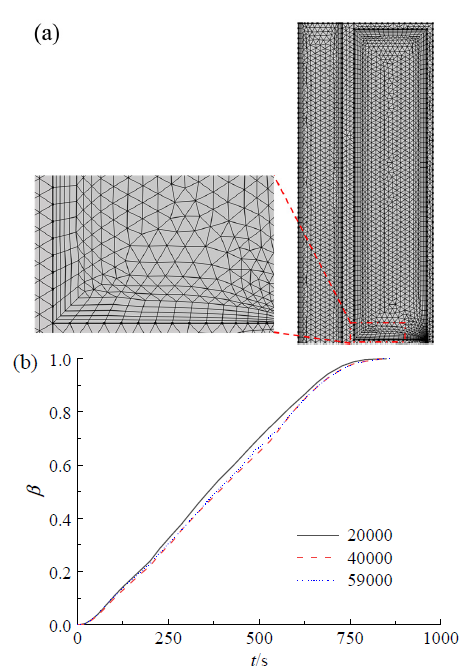
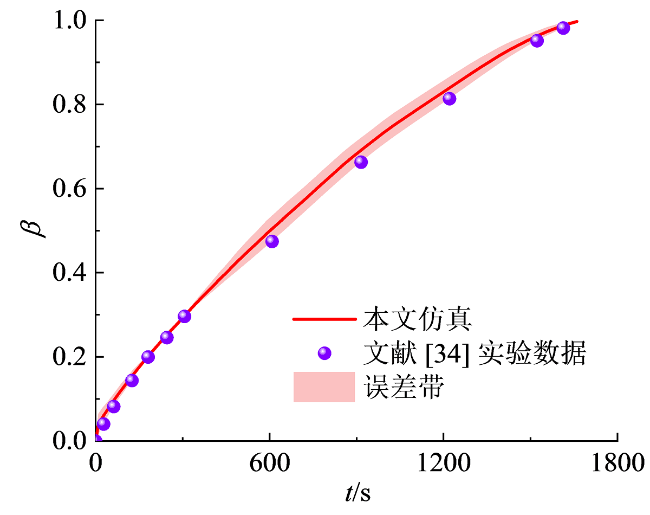
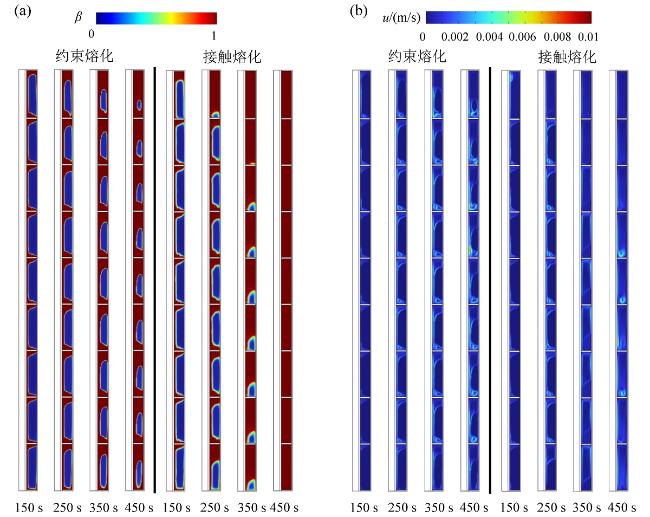
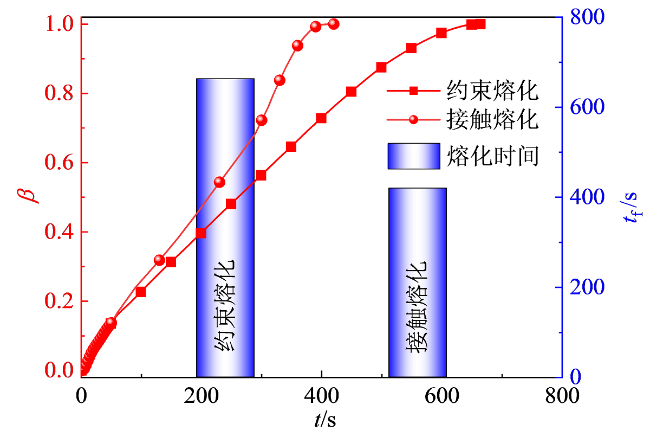
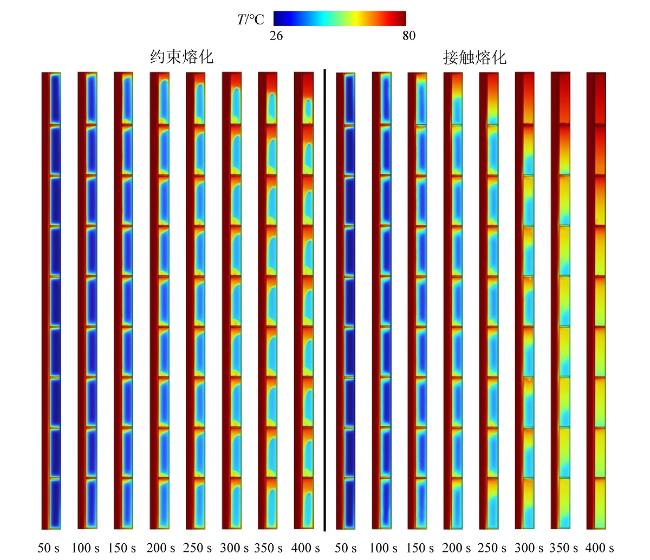
上述潜热存储强化方式在本质上属于被动式技术，无法有效解决储放热过程中由于传热路径增大而导致的潜热储热器换热效率不断衰减的关键难题。在相变材料的熔化过程中，相变材料被局限在固定位置，且随着熔化的进行，熔融层逐渐变厚、传热性能逐渐下降的熔化模式称为约束熔化模式；而相变材料处于自由移动状态且受外力作用下固态相变材料与加热面近距离接触的高效熔化模式称为接触熔化模式[22]。对于潜热储热器的储热过程而言，相变材料在熔化过程难以维持高效传热的接触熔化模式，大多数时间内相变材料还是由约束熔化模式主导。NICHOLAS等[23]最先发现相变材料的接触熔化模式传热速率比非接触熔化模式高出至少一个数量级。因此，如何充分利用接触熔化实现相变材料熔化强化传热成为了国内外普遍关注的前沿热点。鉴于接触熔化传热涉及多个复杂物理过程，学者们一般通过可视化实验观测来揭示接触熔化过程的流动和传热表观特性[24⇓-26]。为探究接触熔化传热机理，学者们通过流动传热微分控制方程开展了一定的理论建模研究。然而，现有研究通常是采用大量假设来构建简化的理论模型，且理论分析大多是基于一维、二维尺度的稳态或准稳态模型[27-28]。伴随计算机技术的飞速发展，焓法模型逐渐发展为模拟固液相变问题的主要工具，并相继发展出全耦合四方程模型[29]（连续性、动量、能量以及力平衡方程）、薄液膜能量平衡法[30-31]以及修正焓−孔隙率模型[32-33]等。然而，这些模型均进行了大量假设导致仿真结果与实验数据差距过大。全耦合四方程模型的精度虽然较高，但计算时间和计算资源消耗过大，难以大规模推广。此外，目前关于接触熔化的研究主要涉及结构相对简单的容器，如球体、圆柱管和矩形腔体。然而，具有复杂结构的潜热储热器中接触熔化性能的研究相对较少，大多数研究成果仅通过实验观察获得。因此，在翅片式潜热储热器中约束熔化和接触熔化的传热机制尚未充分揭示，特别是热对流对这两种熔化模式的影响差异。
为了探究翅片式潜热储热器中约束熔化与接触熔化的传热机制与性能差异，提出一种基于四方程模型的修正等效热容法以研究翅片式潜热储热器中的接触熔化过程。建立一个完全耦合的接触熔化模型，全面考虑固体传导、自然对流和固态相变材料移动等物理过程。同时，比较传统约束熔化和接触熔化过程中翅片式潜热储热器的熔化前沿演化行为、对流特性和动态传热性能。此外，还深入研究换热流体的工作条件对接触熔化传热性能的影响机制。
1 数值模型
1.1 几何模型
表1 相变材料和固体材料的热物性Table 1 Thermophysical properties of phase change material and solid material |
| 参数 | 月桂酸 | 铝合金 |
|---|---|---|
| 相变温度/℃ | 43.5 ~ 48.2 | — |
| 密度/(kg/m3) | 940（固），885（液） | 2 700 |
| 动力黏度/(mPa∙s) | 6.3 | — |
| 比热容/[J/(kg∙K)] | 2 180（固），2 390（液） | 900 |
| 导热系数/[W/(m∙K)] | 0.15 | 150.00 |
| 比潜热/(kJ/kg) | 187.21 | — |
1.2 控制方程
考虑到接触熔化过程涉及热传导、热对流以及固态相变材料移动等复杂物理过程，做出了如下假设以简化接触熔化的数学模型：①相变材料为恒物性，液态下为不可压缩的牛顿流体；②固态相变材料为刚性材质，其下沉过程为准静态运动；③仅在对流项中考虑密度变化，并采用Boussinesq近似诱导自然对流；④忽略惯性力与黏性力的影响。
（1）固液相变守恒方程
基于模型假设，连续性方程及动量方程可简化为如下形式：
$\nabla \cdot \vec{u}=0$
$\rho \frac{\partial \vec{u}}{\partial t}+\rho \nabla \cdot \left( \vec{u}\vec{u} \right)=-\nabla p+\mu {{\nabla }^{2}}\vec{u}+\overrightarrow{{{f}_{b}}}+\overrightarrow{{{f}_{\text{v}}}}$
式中：$\vec{u}$为速度矢量；ρ、μ分别为密度和动力黏度；t为时间；p为压力。浮力项$\overrightarrow{{{f}_{\text{b}}}}$的表达式如下：
$\overrightarrow{{{f}_{b}}}=\rho \vec{g}\alpha \left( T-{{T}_{m}} \right)$
式中：$\vec{g}$为重力加速度，$\vec{g}$ = 9.81 m/s2；α为热膨胀系数；T为相变材料温度；Tm为相变材料熔化区间中间温度。$\overrightarrow{{{f}_{\text{v}}}}$表示体积力源项，被添加到动量方程中以实现速度修正，其表达式如下：
$\overrightarrow{{{f}_{v}}}=-A\left( T \right)\cdot \vec{u}={{C}_{m}}\frac{{{\left( 1-\beta \right)}^{2}}}{{{\beta }^{3}}+0.001}\vec{u}$
式中：A(T)为液相分数β的函数；Cm称为糊状区常数，在本文中取为1 × 107。液相分数的表达式为：
$\beta =\left\{ \begin{align} & \ \ \ 0\ \ \ \ \ \ \ \ T<{{T}_{\text{s}}} \\ & \frac{T-{{T}_{\text{s}}}}{\Delta T}\ \ \ {{T}_{\text{s}}}\le T\le {{T}_{\text{l}}} \\ & \ \ \ 1\ \ \ \ \ \ \ \ T>{{T}_{\text{l}}} \\ \end{align} \right.$
式中：ΔT为相变材料的熔化温度区间；Ts为相变材料熔化起始温度；Tl为相变材料凝固起始温度。
考虑到相变材料熔化传热过程涉及显热和潜热，引入修正的等效热容法以构建适用于未发生相变和考虑潜热效应的相变过程的统一能量方程。
${{c}_{p,\text{e}}}\rho \left( \frac{\partial T}{\partial t}+\vec{u}\cdot \nabla T \right)=\nabla \cdot \left( \lambda \nabla T \right)$
式中：cp,e为等效热容；λ为热导率。cp,e可按照下式计算：
${{c}_{p,\text{e}}}={{c}_{p,\text{s}}}+\beta \left( {{c}_{p,\text{l}}}-{{c}_{p,\text{s}}} \right)+{{L}_{\text{H}}}\cdot D\left( T \right)$
$D\left( T \right)=\frac{\exp \left[ {-\left( T-{{T}_{\text{m}}} \right)}/{{{\left( {\Delta T}/{4}\; \right)}^{2}}}\; \right]}{\sqrt{\text{ }\!\!\pi\!\!\text{ }{{\left( {\Delta T}/{4}\; \right)}^{2}}}}$
式中：LH为相变材料的潜热值；cp为相变材料的比热容，其中下标s表示固体，l表示液体；D(T)为在熔化温度区间内对等效热容进行平滑处理的高斯函数。
对于糊状区相变材料的热物性，可以按照下式计算。
$\rho \left( T \right)={{\rho }_{\text{s}}}+\beta \left( {{\rho }_{\text{l}}}-{{\rho }_{\text{s}}} \right)$
$\lambda \left( T \right)={{\lambda }_{\text{s}}}+\beta \left( {{\lambda }_{\text{l}}}-{{\lambda }_{\text{s}}} \right)$
$\mu \left( T \right)={{\mu }_{\text{l}}}\left[ 1+A\left( T \right) \right]$
（2）力平衡方程
接触熔化过程中固态相变材料在脱离壁面束缚后会发生位置迁移，且实际的移动速度大小和方向均由其受力状态决定。在不考虑外力作用的前提下，接触熔化过程中固态相变材料受到的作用力包括压力、重力、黏性力和惯性力，其力平衡方程如下：
$\begin{align} & \overrightarrow{F}=\overrightarrow{P}+\overrightarrow{D}+\overrightarrow{I}+\overrightarrow{G} \\ & \ \ \ \text{=}-\oint_{S}{p\cdot \text{d}\overrightarrow{S}}+\oint_{S}{\tau \cdot \text{d}\overrightarrow{S}}+\int{{{\rho }_{s}}\cdot \text{d}V\frac{\text{d}\overrightarrow{{{v}_{\mathrm{set}}}}}{\text{d}t}}+\int{\overrightarrow{g}{{\rho }_{s}}\text{d}V} \\ \end{align}$
式中：$\vec{P}$、$\vec{D}$、$\vec{I}$、$\vec{G}$分别为压力、黏性力、惯性力以及重力；$\vec{S}$为固态相变材料的外表面矢量；τ为液态相变材料的应力张量；V为固态相变材料的体积；$\overrightarrow{{{v}_{set}}}$为固态相变材料的移动速度。需要说明的是，接触熔化过程中固态相变材料的移动速度极为缓慢且时间步长通常也较小，因此将惯性力和黏性力忽略。考虑到潜热储热器中的固态相变材料的合力在y方向的分量远远大于x方向的分量，可只考虑y方向的分力以简化问题。因此，力平衡方程可进一步简化为下式。
$\overrightarrow{{{F}_{y}}}=-\oint_{S}{p\cdot \text{d}\overrightarrow{S}}+\int{\overrightarrow{g}{{\rho }_{s}}\cdot \text{d}V}$
此外，将力平衡方程与固态相变材料的移动速度$\overrightarrow{{{v}_{set}}}$耦合作为准静态的判别标准，即存在唯一合适的移动速度$\overrightarrow{{{v}_{set}}}$使得固态相变材料维持力平衡状态。在此基础上，固态相变材料的移动速度$\overrightarrow{{{v}_{set}}}$将可通过修正体积力源项$\overrightarrow{f_{\text{v}}^{'}}$耦合动量方程进行求解，$\overrightarrow{f_{\text{v}}^{'}}$的表达式如下：
$\overrightarrow{f_{v}^{'}}=-A\left( T \right)\left( \overrightarrow{u}-\overrightarrow{{{v}_{set}}} \right)$
（3）初始和边界条件
初始温度设定为26 ℃。潜热储热器的入口温度默认为80 ℃，换热流体的体积流量默认为2 L/min。此外，固体壁面设置为无滑移状态，固液界面为共轭传热面，约束熔化模式与接触熔化模式的初始和边界条件完全一致。
1.3 求解方法
采用一种修正等效热容法计算约束熔化过程[式（1、2、6）]，并提出了一种将商业计算流体力学（computational fluid dynamics, CFD）软件与自编程相结合的方法来求解潜热储热器内的接触熔化过程。图2展示了具体求解过程，基于守恒方程进行修改并融入了界面跟踪和力平衡方程的迭代计算。在初始化后调整动量源项，然后进入当前时间步的熔化过程计算。在每个时间步中，首先需要确定固态相变材料是否满足下沉条件。如果满足下沉条件，则在当前时间步采用界面跟踪方法获取相界面位置并求解力平衡方程以计算移动速度，否则移动速度被假定为0。接下来，将移动速度融入动量源项，并迭代应用于解决动量和能量方程，直至得到满足力平衡收敛标准的移动速度、温度、速度和压力场。守恒方程采用后向欧拉方法进行求解，绝对容差因子为0.05，相对容差设置为0.005。此外，采用结合Secant和Brent方法的组合算法以快速求解力平衡方程。只有在计算残差小于0.01且连续迭代之间的速度容差为1 × 10−7时，才终止力平衡方程的迭代。为了获得良好的收敛性，迭代计算终止准则为容差控制，最大迭代计数为20，容差因子为0.5。
1.4 模型验证
图3（a）展示了计算域的局部网格示意图。由图可见，主体区域采用了具有自适应网格细化的局部三角形网格以提高计算收敛性，而边界区域则采用加密的四边形网格。为了实现更快的收敛速度和更高的计算精度，在迭代求解过程中采用了自适应时间步长。此外，还对接触熔化过程开展了网格独立性验证以排除网格密度对数值计算结果的影响。图3（b）呈现了不同网格数下潜热储热器中接触熔化过程的液相分数变化曲线。此处潜热储热器中的运行工况为：储热器入口温度为70 ℃，换热流体的体积流量为0.1 L/min，其他条件保持默认。由图可知，随着网格数的增加，接触熔化过程的相变材料液相分数曲线趋于重叠。对于潜热储热器中接触熔化过程而言，与网格数为40 000的案例相比，网格数为59 000的案例对应的液相分数的最大相对偏差仅为4.6%。因此，当网格数超过40 000后，数值模拟数据是准确可靠的。
2 结果与讨论
2.1 约束熔化与接触熔化性能对比
图5展示了相同工况下约束熔化和接触熔化中相界面形貌演变特征。对于约束熔化而言，由于传热滞后效应，潜热储热器内上部相变材料的传热温差比下部相变材料大，导致上部相变材料的熔化速度会快于下部相变材料。值得注意的是，接触熔化显示出顶部和底部相变材料的熔化速度更快，而中部相变材料熔化相对较慢。在约束熔化过程中，随着液态相变材料的增加，由自然对流主导的熔化热阻继续增加，使得熔化速度更易受热交换温差的影响。在接触熔化过程中，固态相变材料依次经历约束熔化、固体沉降过程，然后由近距离接触熔化模式主导。考虑到近距离接触熔化模式中的熔化速度快于约束熔化模式，近距离接触熔化的熔化持续时间与固体沉降开始的时间密切相关。此外，正是由于潜热储热器外壳的中部温度最低，固态相变材料开始沉降较晚，从而导致接触熔化过程中潜热储热器中部相变材料的熔化最慢。仔细观察可以发现，约束熔化与接触熔化两种熔化模式下的流动行为与特征存在显著差异，与约束熔化相比，接触熔化中液态相变材料区域的自然对流强度更高。而且，约束熔化过程液态相变材料的最大速度几乎总是出现在熔化前沿，而接触熔化过程则出现在换热管内壁附近。这种现象主要是由于在接触熔化过程中固态相变材料下沉，导致翅片与固态相变材料之间的熔融层液体排出，诱导了液态相变材料区域的混合对流。该混合对流是熔融层排液行为诱发的强迫对流与浮升力引起的自然对流耦合作用的结果，形成了与约束熔化中迥异的流动分布。
图6展示了潜热储热器中不同熔化模式下的液相率曲线演变趋势和完全熔化时间，图中tf表示给定工况下潜热储热器的完全熔化时间。由图可知，约束熔化过程中的熔化速度慢于接触熔化过程。在早期阶段，两种熔化模式下的液相率曲线相对接近。随着液态相变材料的增加，约束熔化过程中的热阻继续增加。然而，接触熔化过程中由于固态相变材料沉降靠近热源而减小了热阻，实现了高效的熔化传热。通过定量统计分析，约束熔化和接触熔化过程的完全熔化时间分别为663 s和420 s。与传统约束熔化相比，高效接触熔化的完全熔化时间缩短了36.7%。这进一步表明，接触熔化可以有效提升翅片式潜热储热器的储热速率。
图7呈现了相同工况下潜热储热器中约束熔化和接触熔化过程的温度分布。由图可知，无论是约束熔化还是接触熔化，潜热储热器上部相变材料区域的热扩散均较快。如前所述，翅片潜热储热器内的接触熔化过程中的热扩散速度要快于传统约束熔化过程。对于约束熔化过程而言，低温固态相变材料和高温翅片之间的熔融层会增加热阻，阻碍热量传递并增大传热路径。相反，接触熔化过程中低温固态相变材料与高温翅片之间的近距离接触会加快相变材料的熔化速度。而且，与传统约束熔化相比，接触熔化过程中液态相变材料区域的热均匀性得到了一定程度的改善。这一现象要归因于接触熔化过程中液态相变材料区域诱发了混合对流，进一步增强了热对流换热能力。
2.2 接触熔化性能的影响因素
图8探究了换热流体的入口温度Tin对翅片储热器内接触熔化过程的影响，其中，平均储热功率qavg表示熔化期间输入到潜热储热器中的热流功率。由图可知，入口温度的升高会降低接触熔化过程的完全熔化时间，但降低的幅度逐渐减小。通过数据分析可知，当入口温度从60 ℃上升至80 ℃时，翅片储热器中接触熔化过程的完全熔化时间缩短了68.8%。当入口温度从80 ℃上升至90 ℃时，翅片储热器中接触熔化过程的完全熔化时间缩短了21.2%。而且，当入口温度从60 ℃上升至90 ℃时，翅片储热器中接触熔化过程的平均储热功率增加了3.5倍。由此可见，提高换热流体的入口温度可以明显提升翅片储热器中接触熔化过程的平均储热功率。
图9展示了换热流体的体积流量Qin对潜热储热器内接触熔化性能的影响。由图可知，随着体积流量的增加，接触熔化过程的完全熔化时间缩短，但变化程度小于入口温度的影响。此外，在体积流量 ≥ 1.5 L/min后，接触熔化过程的完全熔化时间表现出微小变化。当体积流量从0.1 L/min增加到1.5 L/min时，接触熔化过程的完全熔化时间缩短了47.8%。然而，当体积流量从1.5 L/min增加到2 L/min时，接触熔化过程的完全熔化时间仅仅缩短了4.5%。这表明存在一个临界体积流量，超过该值后，接触熔化过程的完全熔化时间几乎保持不变。随着体积流量的增加，接触熔化过程的平均储热功率也相应增加。同样，在体积流量 ≥ 1.5 L/min后，接触熔化过程的平均储热功率趋于稳定。
3 结论与展望
为解决接触熔化的高精度高效率仿真难题，基于修正的等效热容法构建了考虑固体传导、自然对流和固态相变材料运动的全耦合接触熔化传热模型。探讨了翅片式潜热储热器中传统约束熔化和接触熔化过程的相界面熔化行为、对流演化和传热性能。此外，深入分析了换热流体的入口温度和体积流量对高效接触熔化的影响机制。主要结论如下：
（1）约束熔化和接触熔化的早期均由热传导主导传热过程，而熔化后期约束熔化和接触熔化过程中分别诱发了自然对流和混合对流传热模式。
（2）接触熔化的熔化速率和传热均匀性相比传统约束熔化均有所改善。与传统约束熔化相比，翅片式潜热储热器中接触熔化的完全熔化时间缩短了36.7%。
（3）入口温度的升高可以增强接触熔化的性能，但增强程度逐渐减小。随着体积流量的增加，接触熔化传热性能会提高，但变化程度小于入口温度的影响。存在一个临界体积流量，超过该值后，接触熔化传热性能几乎不变。
研究论证了接触熔化相对于约束熔化的储热效率优势，并初步探究了接触熔化性能的影响因素。然而，接触熔化模式下的内在传热机制尚未得到充分揭示。同时，接触熔化的强化传热方式也有待进一步研究。因此，非常有必要开展高效接触熔化的后续研究以推动潜热储热技术的进一步发展。