0 引言
由于世界经济的不断发展和人口的不断增长，石油、煤炭等不可再生能源正在被大量消耗。因此，开发可再生能源越来越受到重视，风能是其中一种清洁的可再生能源[1]。由于风能存在随机性、不稳定性的缺点，风力发电机（wind turbine, WT）的运行状态容易受到风能质量的影响，较差的风能会严重削弱WT发电的质量和稳定性。通过对风能质量进行准确且全面的评估，对于WT的稳定运行和风电场微观选址均具有重要意义。
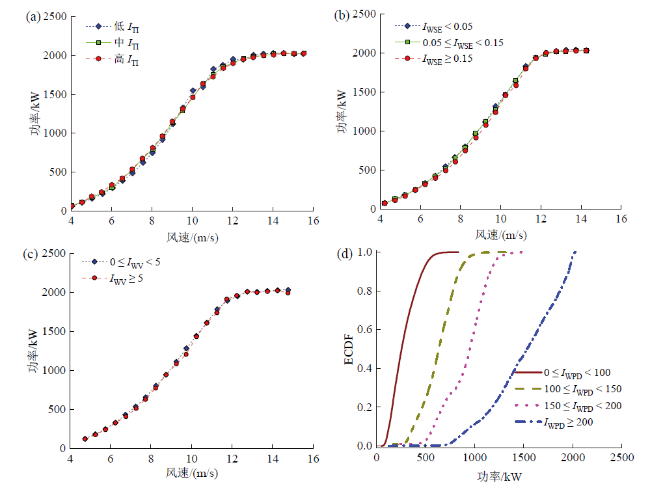
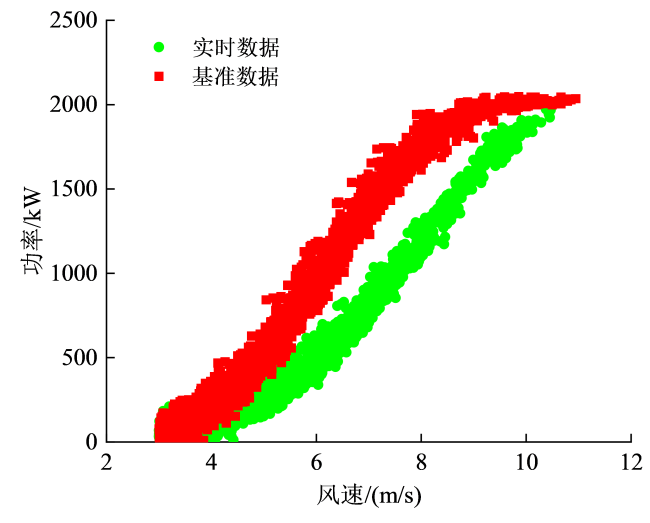
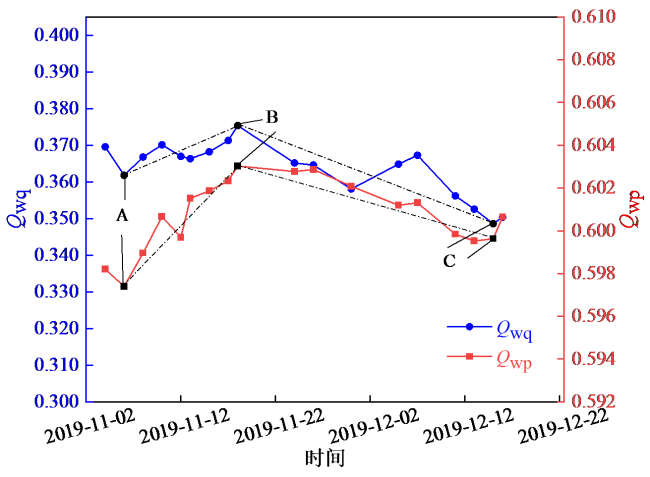
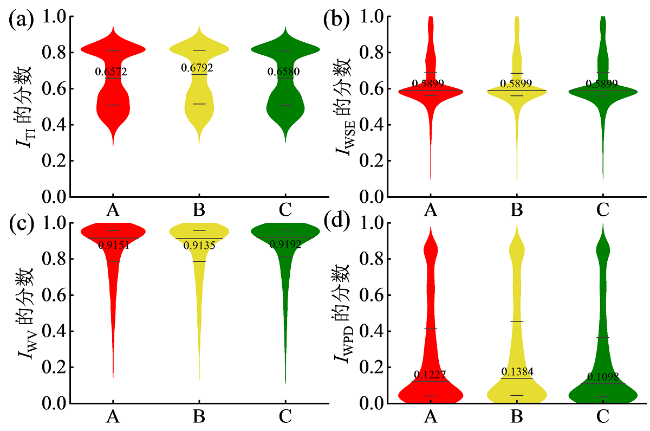
WT的功率一直是制造商、运营商、投资者和电网运营商考虑的重要指标，众多学者通过计算基准功率数据与实时功率数据之间的偏差，对WT发电性能进行实时监测[2⇓⇓⇓⇓-7]。在对WT的发电性能进行评估时，还需要分析影响WT的发电性能下降因素。最常见的影响因素有WT本身控制策略、设备故障和老化[8-9]，此外还有环境因素的影响，如风能质量、结冰、下雨和海浪等。风能质量是影响WT发电性能的关键因素，同时会影响WT的可靠性和安全性。风能指标包括风功率密度、湍流强度、风转向和风切变等，已有多项研究使用风能指标分析了其对WT功率的影响，以及将其用于风电场选址。在对功率的影响方面，BARDAL等[10]发现高湍流使额定风速附近的功率下降，WEN等[11]证明风切变会导致功率损失，SANCHEZ GOMEZ等[12]证明大幅度风向转变会降低WT功率，KIM等[13]的研究证实湍流强度和风切变对发电量有显著影响。在风电场选址中，评估风资源常用风功率密度[14-15]，同时湍流强度也是一个不可忽视的重要指标[16]。目前的研究通常使用单一的风能指标来分析其对WT功率的影响以及在风电场选址中的应用。然而由于复杂的风况变化，单个指标无法全面反映实际风能质量，且具有一定的局限性。在实际风资源评估和WT运维中更加希望获得一个能全面反映风能质量的综合指数，通过该指数可以有效反映不同机位点的风能质量。
针对以上问题，通过分析风能指标对WT功率的影响，构建风能指标评估和评分体系，并提出一种基于调和平均合成的风能质量指数计算方法，同时利用实际的风电场数据，结合WT发电性能指数，验证提出方法的有效性。
1 风能质量指数构建
风能质量是影响WT服役性能的核心因素，风电场受环境因素和机组布局的影响，不同机位点和相同机位点不同时间的风能质量不同。湍流强度、风切变、风转向和风功率密度是影响WT发电性能的关键因素。
1.1 风能指标
1.1.1 湍流强度
湍流强度（ITI）是指风场中湍流运动的强度，是描述风场湍流特性的重要参数。ITI被定义为风速的标准差与平均风速的比值，见式（1）[17]：
${{I}_{\text{TI}}}=\frac{\sigma }{{\bar{v}}}$
1.1.2 风切变
$\left(\frac{V_{2}}{V_{1}}\right)=\left(\frac{H_{2}}{H_{1}}\right)^{\alpha}$
α 也可以用风切变指数（IWSE）表示，根据式（2），IWSE的公式为：
${{I}_{\text{WSE}}}={\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)}/{\ln \left( \frac{{{H}_{2}}}{{{H}_{1}}} \right)}\;$
1.1.3 风转向
风转向（IWV）是指风向随高度的变化，可以根据以下公式计算IWV随高度的线性变化[21]。
${{I}_{\text{WV}}}={\left( d-{{d}_{\text{hub}}} \right)}/{\left( h-{{h}_{\text{hub}}} \right)}\;$
1.1.4 风功率密度
${{E}_{\text{pf}}}=\frac{\frac{1}{n}\sum\limits_{i=1}^{n}{V_{i}^{3}}}{{{\left( \frac{1}{n}\sum\limits_{i=1}^{n}{{{V}_{i}}} \right)}^{3}}}$
$k=1+\frac{3.69}{E_{\text{pf}}^{2}}$
$c=\frac{\bar{V}}{\Gamma\left(1+\frac{1}{k}\right)}$
式中：Epf为能量模式因子；n为计算IWPD时间段内的风速数量；Vi为该时间段内第i个风速；$\bar{V}$为平均风速。
然后根据式（6）、式（7），IWPD被定义为：
${{I}_{\text{WPD}}}=\frac{1}{2}\times \rho \times {{c}^{3}}\times \Gamma \left( 1+\frac{3}{k} \right)$
式中：ρ为空气密度。
1.2 风能质量指数合成
风能质量指数的构建包括各项指标分数分配与合成。根据1.1节的分析结果，将ITI、IWSE、IWV和IWPD四个指标按表1的形式进行分级，根据不同等级对功率影响的区别，使用线性插值方法进行分数分配。此外，在研究中，风速范围限定在切入风速vin ~ vrated之间。假设有r项指标，l个样本，形成原始指标数据矩阵为：
$\mathbf{X}=\left( \begin{matrix} {{x}_{11}} & \cdots & {{x}_{1r}} \\ \vdots & \ddots & \vdots \\ {{x}_{l1}} & \cdots & {{x}_{lr}} \\\end{matrix} \right)$
式中：xlr为第l个样本的第r项指标。利用表1可以计算xlr对应的分数值，用slr表示。完成所有指标值的评分后，形成分数矩阵（S）为：
$\mathbf{S}=\left( \begin{matrix} {{s}_{11}} & \cdots & {{s}_{1r}} \\ \vdots & \ddots & \vdots \\ {{s}_{l1}} & \cdots & {{s}_{lr}} \\\end{matrix} \right)$
指标合成采用调和平均合成方法[23]，具体公式如下：
${{E}_{i}}=\frac{n}{\frac{1}{{{s}_{i1}}}+\frac{1}{{{s}_{i2}}}+\frac{1}{{{s}_{i3}}}+\cdots +\frac{1}{{{s}_{ir}}}}$
式中：Ei为第i个样本的合成结果。一段时间（t）内的风能质量指数可以表示为：
${{Q}_{\text{wq}}}=\frac{1}{t}\sum\limits_{i=1}^{t}{{{E}_{i}}}$
当Qwq越接近于1，表明风能质量越好；当Qwq越接近于0，表明风能质量越差。
表1 风能指标等级划分Table 1 Wind energy indicator classification |
| 指标 | 等级 | 分数 |
|---|---|---|
| ITI | 0 ~ 0.15 | 0.00 → 0.60 |
| 0.15 ~ 0.20 | 0.60 → 0.80 | |
| > 0.20 | 0.80 → 1.00 | |
| IWSE | 0 ~ 0.05 | 1.00 → 0.80 |
| 0.05 ~ 0.15 | 0.80 → 0.60 | |
| ≥ 0.15 | 0.60 → 0.00 | |
| IWV | 0 ~ 5 | 1.00 → 0.60 |
| ≥ 5 | 0.60 → 0.00 | |
| IWPD | 0 ~ 100 | 0.00 → 0.60 |
| 100 ~ 150 | 0.60 → 0.75 | |
| 150 ~ 200 | 0.75 → 0.85 | |
| ≥ 200 | 0.85 → 1.00 |
注：风速范围为vin < v < vrated。 |
2 发电性能指数
（1）从风场中选择一台性能稳定且维修较少的WT作为基准，在其远程中央监控与数据采集（supervisory control and data acquisition, SCADA）系统数据中提取一组满足v∈[vin,vrated]的数据作为该风场的评估基准。
（2）同样，实时数据也需满足v∈[vin,vrated]。之后按照时间窗口（T）和滑动步长（ΔT）的大小划分基准和实时数据。划分完毕后，用基于密度的噪声应用空间聚类（density-based spatial clustering of applications with noise, DBSCAN）算法对每个T内的数据进行预处理。
（3）根据T的大小，将T划分为N个风速箱（Vbin）。在第ni个Vbin中，ECDF的计算公式为：
$F_{{{n}_{i}}}^{0}\left( P \right)=\frac{1}{{{m}_{1}}}\sum\limits_{{{n}_{j}}=1}^{{{m}_{1}}}{Z\left[ P_{{{n}_{i}},{{n}_{j}}}^{0}\le P \right]}$
${{F}_{{{n}_{i}}}}\left( P \right)=\frac{1}{{{m}_{2}}}\sum\limits_{{{n}_{j}}=1}^{{{m}_{2}}}{Z\left[ {{P}_{{{n}_{i}},{{n}_{j}}}}\le P \right]}$
式中：Z为指示函数；m1、m2分别为基准数据和实际数据在第ni个Vbin中的数量；P为功率；$P_{{{n}_{i}},{{n}_{j}}}^{0}$为表示基准数据第ni个Vbin中第nj个功率；${{P}_{{{n}_{i}},{{n}_{j}}}}$为实时数据第ni个Vbin中第nj个功率；nj为Vbin的点数。
（4）利用式（13）和式（14），计算第ni个Vbin基准数据与实时数据之间的偏差（${{M}_{{{n}_{i}}}}$）：
$\bar{P}_{{{n}_{i}}}^{0}=\frac{1}{{{m}_{1}}}\sum\limits_{{{n}_{j}}=1}^{{{m}_{1}}}{P_{{{n}_{i}},{{n}_{j}}}^{0}}$
${{M}_{{{n}_{i}}}}=\frac{1}{\bar{P}_{{{n}_{i}}}^{0}}\int\limits_{-\infty }^{+\infty }{\left| F_{{{n}_{i}}}^{0}\left( P \right)-{{F}_{{{n}_{i}}}}\left( P \right) \right|\text{d}P}$
式中：$\bar{P}_{{{n}_{i}}}^{0}$为第ni个Vbin基准数据的功率平均值。
（5）计算完所有Vbin的${{M}_{{{n}_{i}}}}$后，需要计算每个Vbin的加权值，第ni个Vbin的加权值（${{K}_{{{n}_{i}}}}$）计算公式如下：
${{K}_{{{n}_{i}}}}=\frac{f\left( v_{{{n}_{i}}}^{\text{mean}} \right)}{\sum\limits_{{{n}_{i}}=1}^{n}{f\left( v_{{{n}_{i}}}^{\text{mean}} \right)}}$
式中：$f\left( v_{{{n}_{i}}}^{\text{mean}} \right)$为标准功率曲线的功率；$v_{{{n}_{i}}}^{\text{mean}}$为基准数据在第ni个Vbin的平均值。
（6）根据式（16）和式（17）计算T中风速区间为v∈[vin,vrated]的发电性能指数：
${{Q}_{\text{wp}}}=1-\sum\limits_{{{n}_{i}}=1}^{N}{{{K}_{{{n}_{i}}}}{{M}_{{{n}_{i}}}}}$
当Qwp接近于1，表明WT的发电性能较好；Qwp接近于0，表明WT的发电性能较差。通过这一指标可以判断WT的运行状态及稳定性。
3 实例验证
本文使用的SCADA数据以及测风塔数据都来源于中国南方一个山地风电场，该风电场使用的是2 MW直驱永磁水平轴WT，其直径为93 m，vin为3 m/s，vrated为11 m/s，切出风速为25 m/s，额定功率为2 000 kW。
3.1 案例1
选择数据采集时间为2019年9月至2019年12月且靠近测风塔的WT进行验证，其中WT轮毂高度与测风塔80 m的风速数据的相关性系数为0.7，检验值接近于0，表明两组数据具有显著的强相关性。因此，可以将测风塔上的IWSE和IWV视为WT对应位置上的IWSE和IWV。风能质量指数构建方法的输入x1、x2、x3、x4分别为ITI、IWSE、IWV和IWPD，其中ITI、IWPD用SCADA数据计算，IWSE、IWV用测风塔数据计算。
在图3中，数据集按时间T为29 d，∆T为1 d的形式划分，并计算每个T内的Qwp与Qwq。由图可知，在2019年11月22日之前，Qwq先从0.370下降至0.362再回升至0.375，Qwp则先从0.598下降至0.597，随后再上升至0.603，两条曲线在该时间段内同时表现出先下降后上升的趋势。在2019年11月22日至2019年12月31日，Qwq从0.375下降至0.349，再微弱上升到0.350；Qwp从0.603下降至0.599附近再微弱上升到0.601，整体上，在该时间段内两条曲线依然呈现出先下降后上升的趋势。峰值点从Qwp曲线和Qwq曲线中选择，分别标记为A至C，并用黑色点划线连接，可以发现两条点划线均出现先上升后下降的趋势，两者的皮尔逊相关系数为0.606。由此看来，Qwq与Qwp的变化趋势大致相同。
为进一步验证风能质量指数构建方法的有效性，绘制了A、B、C日期处的指标分数小提琴图。水平形状表示概率密度，垂直形状反映分布特征，如图4所示。在图4（a）中，B处的ITI得分的中位数、第一四分位数和第三四分位数均高于A和C。在0.6以下区域，B处的水平形状比A和C更细，表示B处的低分数量较少，高分数量较多。图4（b、c）显示A、B、C中IWSE和IWV的得分分布相似。图4（d）中，B处的IWPD得分的中位数、第一四分位数和第三四分位数均大于A和C。在0.7以上区域，B处的水平形状比A和C更粗，表明B处的高分数量较多，低分数量较少。A处的第一四分位数比C大，表明A处的高分数量多于C。上述分析表明，B处出现极大值，A、C处出现极小值是合理的。因此Qwq可以直观反映风能质量，并结合PAM分析法，可以快速发现WT的发电性能下降的原因。
3.2 案例2
在某些机位无法计算所有指标时，采用剩余指标构建风能指标数据矩阵。为了验证在指标缺失情况下所提出方法的有效性，本案例选择风电场内7台WT在2019年9月至12月期间的SCADA数据，计算其在此期间的ITI和IWPD，并将其作为输入，形成7个风能指标矩阵，同时计算这7个机位点的Qwq。
数据集按时间T为29 d，∆T为1 d的形式划分，并计算每个T内的Qwp和Qwq。从图5可以看出，WT16的Qwq和Qwp曲线的表现最优。然而，WT16在所选时间段的前期因故障停机，风速和功率数据记录为0并被清除。后期，WT16修复后，Qwp从0.699上升至0.708。在此期间，Qwq在0.701 ~ 0.709的范围内波动，但波动范围仅有0.008，表明风资源变化较小，对刚修复并重新启动的WT影响有限。WT22的Qwq和Qwp略低，分别分布在0.680 ~ 0.695和0.644 ~ 0.647。WT12的Qwq为0.664 ~ 0.681，Qwp为0.625 ~ 0.643，均低于WT16和WT22。WT18的Qwq和Qwp曲线较低，在0.660和0.620左右。除此之外，WT14、WT13、WT17的Qwq曲线逐条向下排布，相应的Qwp曲线也随之逐条减小。表2可以看出这7台WT的Qwp,mean与Qwq,mean的排序结果一致。
表2 两种平均评价值及排序结果Table 2 Two types of average evaluation values and ranking results |
| WT编号 | Qwp | Qwq | ||
|---|---|---|---|---|
| Qwp,mean | 排序 | Qwq,mean | 排序 | |
| WT12 | 0.637 2 | 3 | 0.672 4 | 3 |
| WT13 | 0.559 2 | 6 | 0.644 2 | 6 |
| WT14 | 0.579 1 | 5 | 0.653 4 | 5 |
| WT16 | 0.703 5 | 1 | 0.704 0 | 1 |
| WT17 | 0.555 6 | 7 | 0.590 0 | 7 |
| WT18 | 0.621 5 | 4 | 0.664 7 | 4 |
| WT22 | 0.645 2 | 2 | 0.688 8 | 2 |
图7展示了A、B、C所代表的功率数据以及基准功率数据。在这些数据中，A、B和C分别对应的Qwq值为0.71、0.65和0.57，相应的Qwp值为0.71、0.59和0.55。可以发现，对于Qwq和Qwp，均遵循1 > A > B > C。因此，这些点的功率散点均分布在基准功率散点的下方。进一步分析发现，A处的功率散点分布在B处的功率散点上方，B处的功率散点位于A与C之间，而C处的功率散点总体分布在最低位置。这种分布特征清晰地揭示了Qwq对WT发电性能的影响趋势，为本文提出方法的有效性提供了直观的证据。
4 结论
提出了基于调和平均合成的风能质量指数构建及评估方法，并将其应用到实际风场运行的数据上，结果表明：
（1）该方法能够对WT受到的风资源质量进行有效的量化。
（2） 利用该方法计算得到的Qwq结合PAM计算得到的Qwp进行综合分析，验证了Qwq能够有效反映风能质量。
（3）对于同一台WT，Qwq与Qwp呈现相同的变化趋势；对于多台WT，Qwq与Qwp呈现相同的排序。验证了提出风能质量指数构建方法和评分体系的有效性和合理性。
此外，该方法通俗易懂，能够容易被检修人员理解和掌握，并为检修人员提供了理论参考。在WT的运行状态下降时，不能只考虑故障因素，也要注重风能质量。